6 Sets and Counting Sets and Set Operations

6 Sets and Counting • Sets and Set Operations • The Number of Elements in a Finite Set • The Multiplication Principle • Permutations and Combinations

Section 6. 1 Sets and Set Operations Set: A set is a collection of objects/elements. Ex. A = {w, a, r, d} Sets are often named with capital letters. Order of elements doesn’t matter, no duplicates. Notation: w is an element of set A is written Set-builder notation: rule describes the definite property (properties) an object x must satisfy to be part of the set. Ex. B = {x | x is an even integer} Read: “x such that x is an even integer” Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Set Terminology and Notation Set Equality: Two sets A and B are equal, written A = B, if and only if they have exactly the same elements. Ex. A = {w, a, r, d}; B = {d, r, a, w} Every element in A is in B and every element in B is in A. Subset: If every element of a set A is also an element of a set B then A is a subset of B, written Ex. A = {r, d}; B = {r, a, w, d, e, t} Every element in A is also in B Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Set Terminology and Notation Cont. Empty Set: The set that contains no elements is called the empty set and is denoted Note: The empty set is a subset of every set Universal Set: The set of all elements of interest in a particular discussion is called the universal set and is denoted U. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Set Operations Set Union: Let A and B be sets. The union of A and B, written the set of all elements that belong to either A or B. is Set Intersection: Let A and B be sets. The intersection of A and B, written is the set of all elements that are common to A and B. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex. Given the sets: Combine the sets Overlap of the sets Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

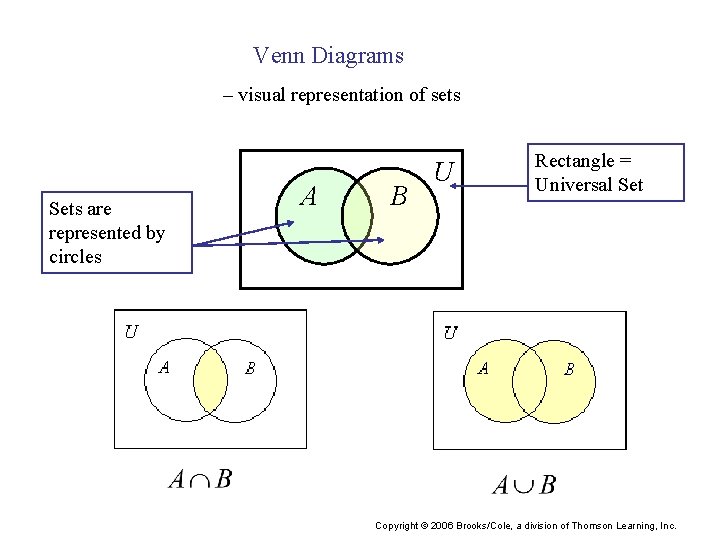
Venn Diagrams – visual representation of sets Sets are represented by circles A B U Rectangle = Universal Set Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

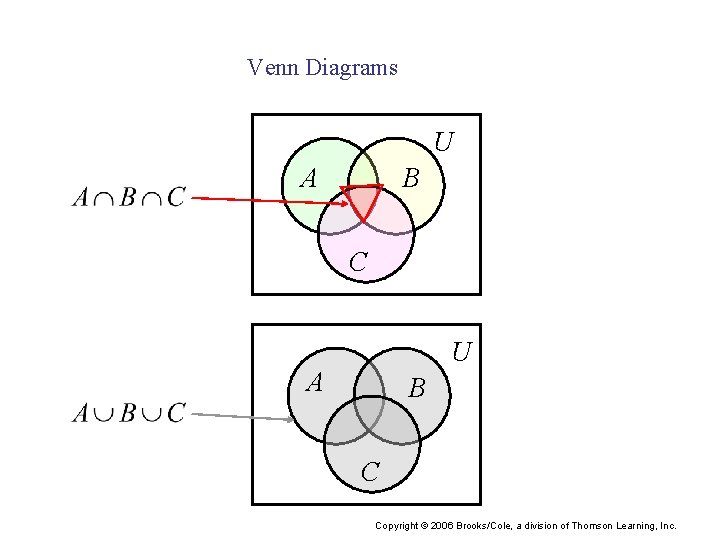
Venn Diagrams U A B C Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

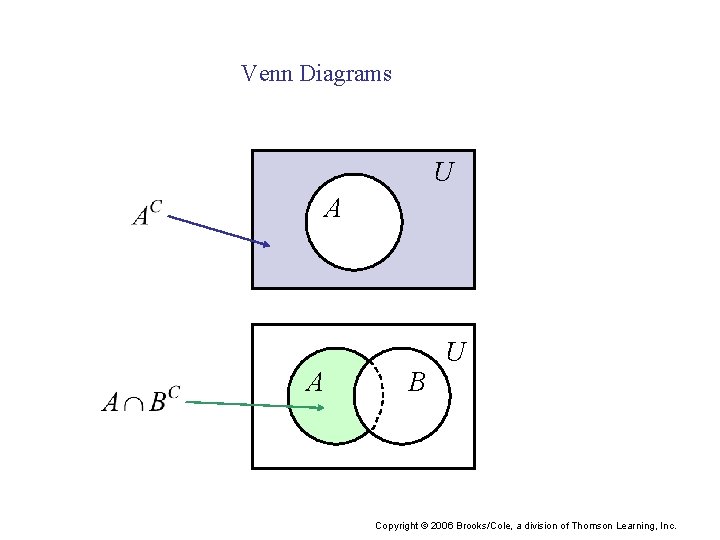
Complement of a Set: If U is a universal set and A is a subset of U, then the set of all elements in U that are not in A is called the complement of A, written AC. Set Complementation Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Set Operations Commutative Laws Associative Laws Distributive Laws Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

De Morgan’s Laws Let A and B be sets, then Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex. Given the sets: Elements not in A. Elements in A and not in B. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Venn Diagrams U A A B U Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Section 6. 2 The Number of Elements in a Set The number of elements in a set A is denoted n(A). Ex. Given n(A) = 4 Notice Since the union doesn’t count a and h twice This leads to Overlap is subtracted Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Venn Diagram – number of elements 22 A 12 5 B U 31 We can see that So which leads to Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

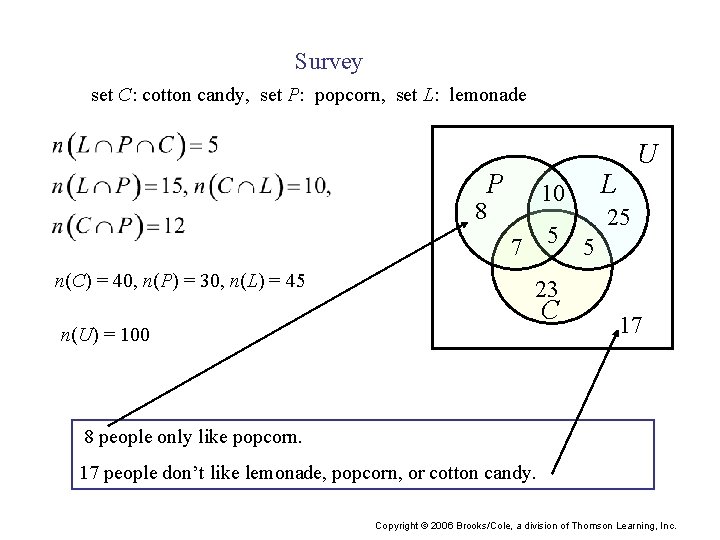
Survey In a survey of 100 people at a carnival: 40 like cotton candy 30 like popcorn 45 like lemonade 15 like lemonade and popcorn 10 like cotton candy and lemonade 12 like cotton candy and popcorn 5 like all three How many people don’t like lemonade, popcorn, or cotton candy? How many people only like popcorn? Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Survey set C: cotton candy, set P: popcorn, set L: lemonade P 5 7 n(C) = 40, n(P) = 30, n(L) = 45 L 10 8 U 25 5 23 C n(U) = 100 17 8 people only like popcorn. 17 people don’t like lemonade, popcorn, or cotton candy. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Section 6. 3 The Multiplication Principle If there are m ways of performing a task T 1 and n ways of performing a task T 2, then there are mn ways of performing task T 1 followed by task T 2. Note: This generalizes to the multiplication principle involving more than two tasks. Ex. A man has a choice of 8 shirts and 3 different pants. How many outfits can the man wear? Considering shirts as task 1 and pants as task 2, we have 8(3) = 24 outfits Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex. How many outcomes are possible for a game that consists of rolling a die followed by flipping a fair coin? 6 possibilities 2 possibilities Total of 6(2) = 12 outcomes Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex. An employee ID for a particular company consists of the employee’s first initial, last initial, and last four digits of his/her social security number. How many possible ID’s are there? Each Initial has 26 possibilities (A–Z) and each digit has 10 possibilities (0– 9) 26(26)(10)(10) = 6760000 different IDs possible Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Section 6. 4 Permutations and Combinatons A permutation of a set of objects is an arrangement of these objects in a definite order. A combination is a selection of r objects from a set of n objects where order is not important Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

n–Factorial For any natural number n, Ex. 5! = 5(4)(3)(2)(1) = 120 Ex. This notation allows us to write expressions associated with permutations and combinations in a compact form. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Permutations of n Distinct Objects The number of permutations of n distinct objects taken r at a time is given by Ex. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex. A boy has 4 beads – red, white, blue, and yellow. How different ways can three of the beads be strung together in a row? This is a permutation since the beads will be in a row (order). total number selected 24 different ways Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Permutations of n Objects, Not all Distinct Given n objects with n 1 (non-distinct) of type 1, n 2 (non-distinct) of type 2, …, nr (non-distinct) of type r where n = n 1 + n 2 + … + nr then the number of permutations of these n objects taken n at a time is given by Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

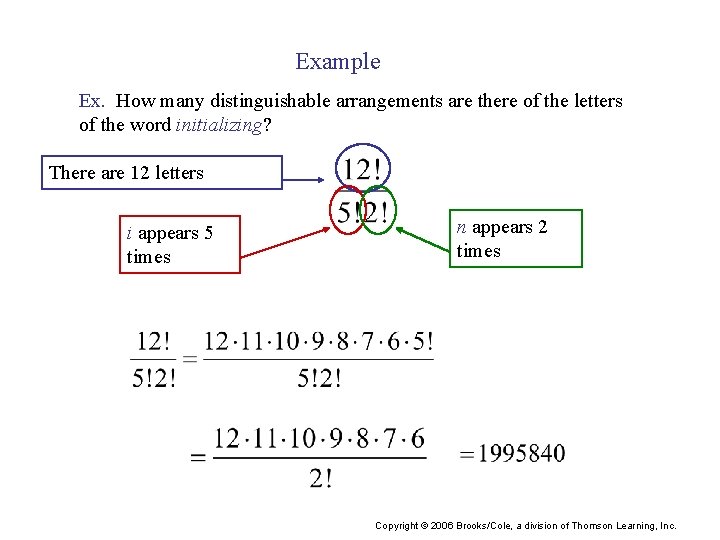
Example Ex. How many distinguishable arrangements are there of the letters of the word initializing? There are 12 letters i appears 5 times n appears 2 times Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Combinations of n Objects The number of combinations of n distinct objects taken r at a time is given by Ex. Find C(9, 6). = 84 Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

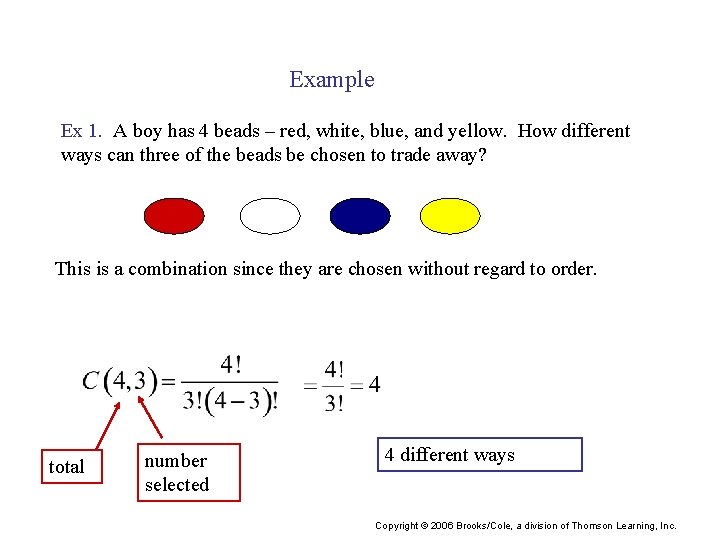
Example Ex 1. A boy has 4 beads – red, white, blue, and yellow. How different ways can three of the beads be chosen to trade away? This is a combination since they are chosen without regard to order. total number selected 4 different ways Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Ex 2. A space shuttle crew consists of a shuttle commander, a pilot, three engineers, a scientist, and a civilian. The shuttle commander and pilot are to be chosen from 8 candidates, the three engineers from 12 candidates, the scientist from 5 candidates, and the civilian from 2 candidates. How many such space shuttle crews can be formed? Solution: There are P(8, 2) ways of picking the shuttle commander and pilot (the order is important here), C(12, 3) ways of picking the engineers (the order is not important here), C(5, 1) ways of picking the scientist, and C(2, 1) ways of picking the civilian. . Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

By the multiplication principle: Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.