Lecture 3 Set Operations Set Functions Recap Set

Recap • • • Set: unordered collection of objects Equal sets have the same

1. 7 Set Operations Union: The union of 2 sets A and B is

1. 7 Set Operations Intersection: The intersection of 2 sets A and B is

1. 7 Set Operations Sets are disjoint if their intersection is the empty set.

1. 7 Set Operations Difference: The difference between 2 sets A and B is

1. 7 Set Operations Complement: The complement of a set A in U is

1. 7 Set Operations Set identities: U A Morgan’s law A B

1. 7 Set Operations Membership tables (just like truth tables): Generalized Union: The union

1. 7 Set Operations Example: Ai = {i, i+1, i+2. . } Efficient representation

1. 8 Functions function: The assignment of exactly one element of the set B

1. 8 Functions If f 1 and f 2 are two functions from A

1. 8 Functions One-to-one or injective function: A function f is one-to-one if and

1. 8 Functions strictly increasing strictly decreasing x, y real decreasing increasing f(x) >

1. 8 Functions Onto or surjective functions: A function f from A to B

1. 8 Functions One-to-one correspondence or bijection: A function f is in one-to-one correspondence

1. 8 Functions Inverse function: The inverse function of a bijection is the function

1. 8 Functions Composition: A composition of 2 functions g: A B and f:

Slides: 18

Download presentation

Lecture 3 Set Operations & Set Functions

Recap • • • Set: unordered collection of objects Equal sets have the same elements Subset: elements in A are also in B Power-set: set of all subsets Cartesian Product: set of ordered pairs.

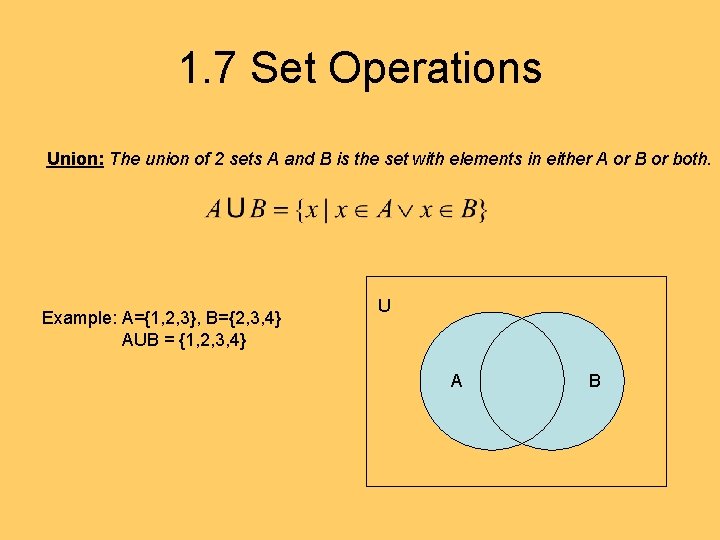
1. 7 Set Operations Union: The union of 2 sets A and B is the set with elements in either A or B or both. Example: A={1, 2, 3}, B={2, 3, 4} AUB = {1, 2, 3, 4} U A A B

1. 7 Set Operations Intersection: The intersection of 2 sets A and B is the set containing elements in both A and B. Example: A={1, 2, 3}, B={2, 3, 4} A B = {2, 3} U A A B

1. 7 Set Operations Sets are disjoint if their intersection is the empty set. I. e. They have no elements in common. Principle of inclusion-exclusion: Example: A={1 2 3}, B = {p, q, r}. A and B are disjoint. |AUB|=|A|+|B|=6 Example: A={1 2 3}, B={1 2 3}. A=B. |AUB|=3+3 -3=3. this terms is needed because elements both in A and B are counted once in AUB.

1. 7 Set Operations Difference: The difference between 2 sets A and B is the set with elements in A but not in B. Example: A={1 2 3}, B={2 3 4} A-B={1} U A A B

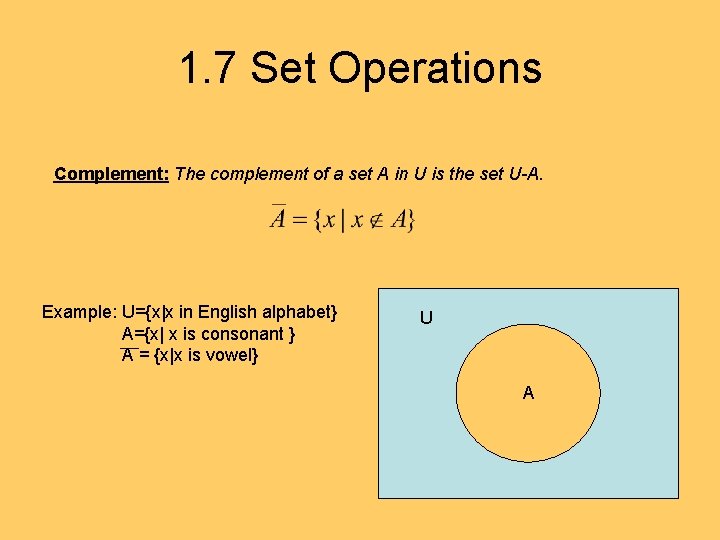
1. 7 Set Operations Complement: The complement of a set A in U is the set U-A. Example: U={x|x in English alphabet} A={x| x is consonant } A = {x|x is vowel} U A

1. 7 Set Operations Set identities: U A Morgan’s law A B

1. 7 Set Operations Membership tables (just like truth tables): Generalized Union: The union of a collection of sets is the set with elements in at least one of the sets in the collection. Generalized intersection: The intersection of a collection of sets is the set with elements in all sets in the collection.

1. 7 Set Operations Example: Ai = {i, i+1, i+2. . } Efficient representation in a computer: Assume arbitrary order and denote set membership with a bit string: U={1, 2, . . . 10} (in this order) A = {1 2 3 4 5}=1 1 1 0 0 0 B = {4, 5, 6} = 0 0 0 1 1 1 0 0 AUB = 1 1 1 0 0 = BIT-wise AND = {1 2 3 4 5 6} Examples on white board

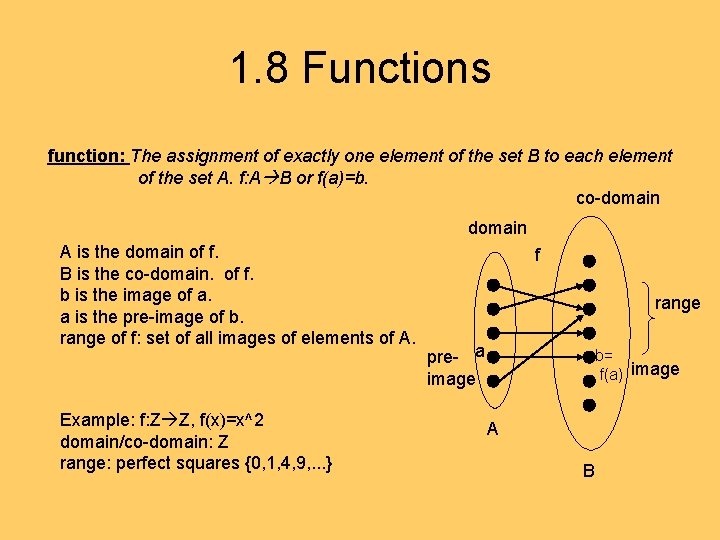
1. 8 Functions function: The assignment of exactly one element of the set B to each element of the set A. f: A B or f(a)=b. co-domain A is the domain of f. B is the co-domain. of f. b is the image of a. a is the pre-image of b. range of f: set of all images of elements of A. Example: f: Z Z, f(x)=x^2 domain/co-domain: Z range: perfect squares {0, 1, 4, 9, . . . } f range pre- a image b= f(a) image A B

1. 8 Functions If f 1 and f 2 are two functions from A to R (real numbers), then g=f 1+f 2 and h=f 1*f 2 are also functions defined by: (f 1+f 2)(x) = f 1(x) + f 2(x) (f 1*f 2)(x) = f 1(x)*f 2(x) Example: f 1(x) = x, f 2(x) = x^2. (f 1+f 2)(x) = x+x^2 (f 1*f 2)(x) = x^3. f: A B, and S is a subset of A. Then we can define f: S Image(S)=f(S) f A S f(S) B

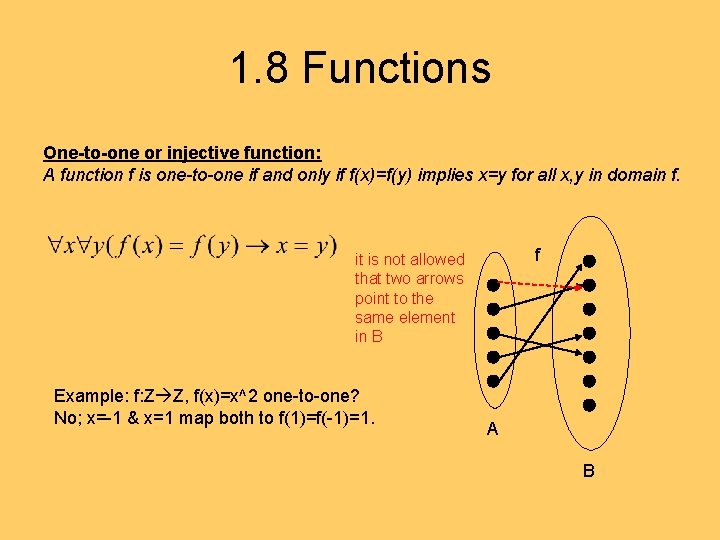
1. 8 Functions One-to-one or injective function: A function f is one-to-one if and only if f(x)=f(y) implies x=y for all x, y in domain f. f it is not allowed that two arrows point to the same element in B Example: f: Z Z, f(x)=x^2 one-to-one? No; x=-1 & x=1 map both to f(1)=f(-1)=1. A B

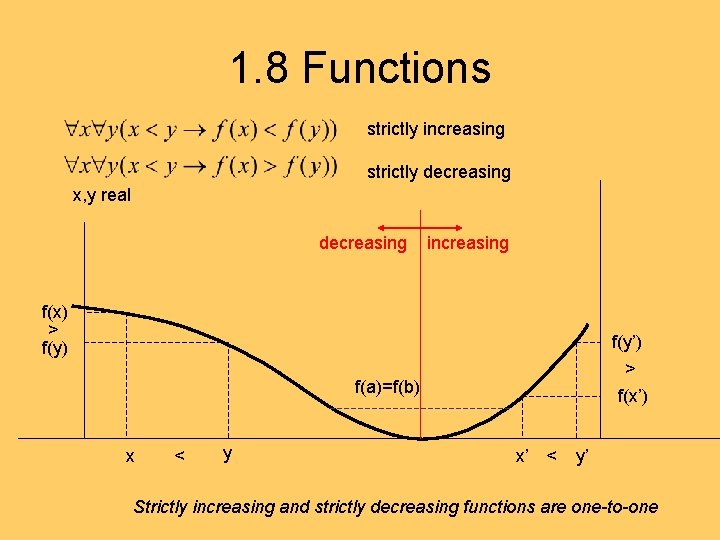
1. 8 Functions strictly increasing strictly decreasing x, y real decreasing increasing f(x) > f(y) f(y’) > f(x’) f(a)=f(b) x < y x’ < y’ Strictly increasing and strictly decreasing functions are one-to-one

1. 8 Functions Onto or surjective functions: A function f from A to B is onto if for every element b in B there is an element a in A with f(a)=b. x y f Example: F: Z Z, f(x)=x^2 onto? No, y=-1 has no pre-image. A B There is no element without incoming arrows

1. 8 Functions One-to-one correspondence or bijection: A function f is in one-to-one correspondence if it is both one-to-one and onto. Number of elements in A and B must be the same. Every element in A is uniquely associated with exactly one element in B. Example: f: R R, f(x)= -x f bijection! A B

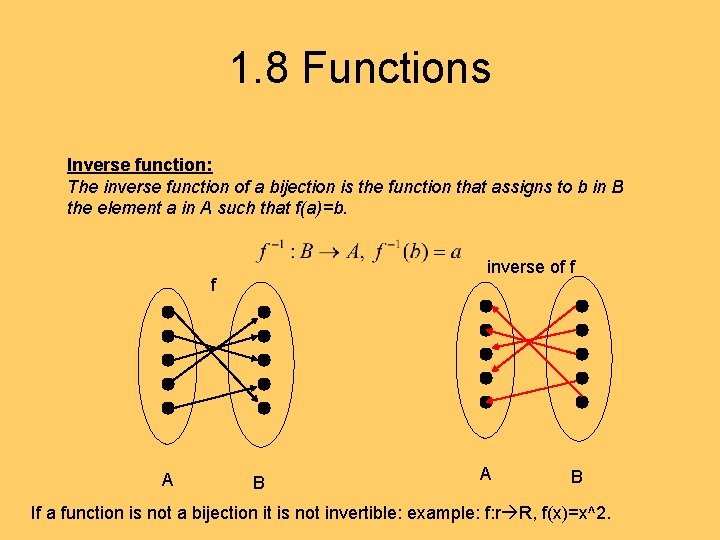
1. 8 Functions Inverse function: The inverse function of a bijection is the function that assigns to b in B the element a in A such that f(a)=b. inverse of f f A B If a function is not a bijection it is not invertible: example: f: r R, f(x)=x^2.

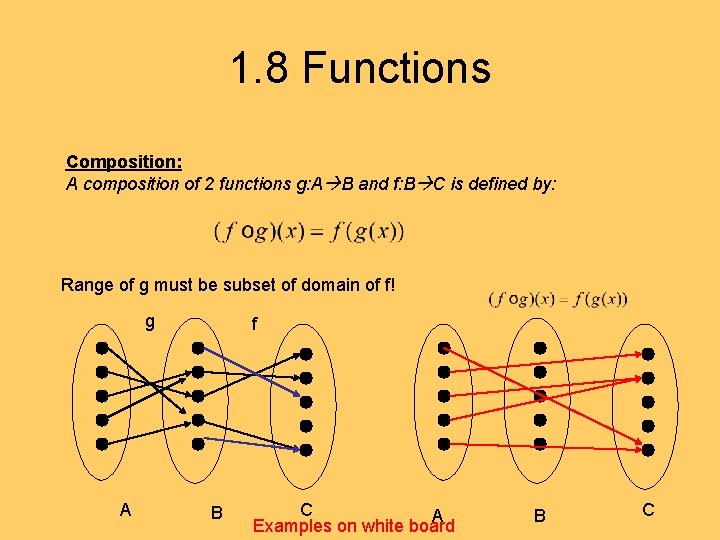
1. 8 Functions Composition: A composition of 2 functions g: A B and f: B C is defined by: Range of g must be subset of domain of f! g A f B C A Examples on white board B C