Section 6 6 Graphs of Transformed Sine and

Section 6. 6 Graphs of Transformed Sine and Cosine Functions Copyright © 2013, 2009, 2006, 2001 Pearson Education, Inc.

Objectives Graph transformations of y = sin x and y = cos x in the form y = A sin (Bx – C) + D and y = A cos (Bx – C) + D and determine the amplitude, the period, and the phase shift. · Graph sums of functions. · Graph functions (damped oscillations) found by multiplying trigonometric functions by other functions. ·

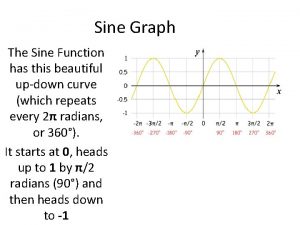
Variations of the Basic Graphs We are interested in the graphs of functions in the form y = A sin (Bx – C) + D and y = A cos (Bx – C) + D where A, B, C, and D are all constants. These constants have the effect of translating, reflecting, stretching, and shrinking the basic graphs.

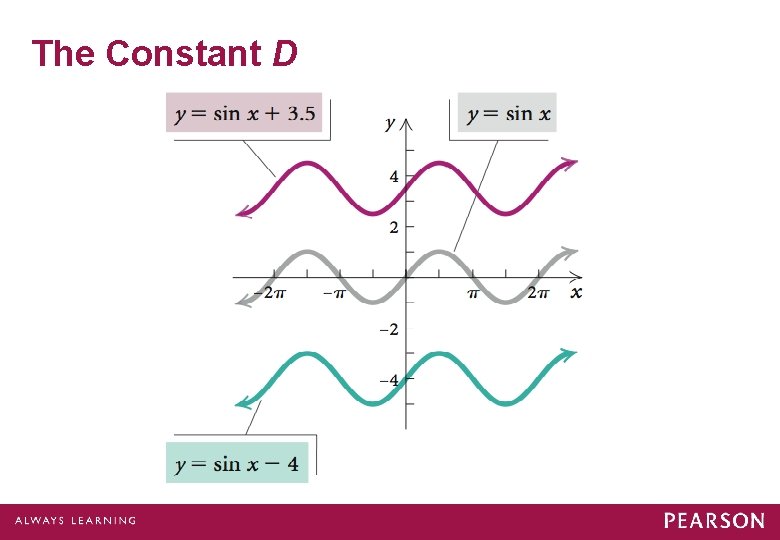
The Constant D Let’s observe the effect of the constant D.

The Constant D

The Constant D The constant D in y = A sin (Bx – C) + D and y = A cos (Bx – C) + D translates the graphs up D units if D > 0 or down |D| units if D < 0.

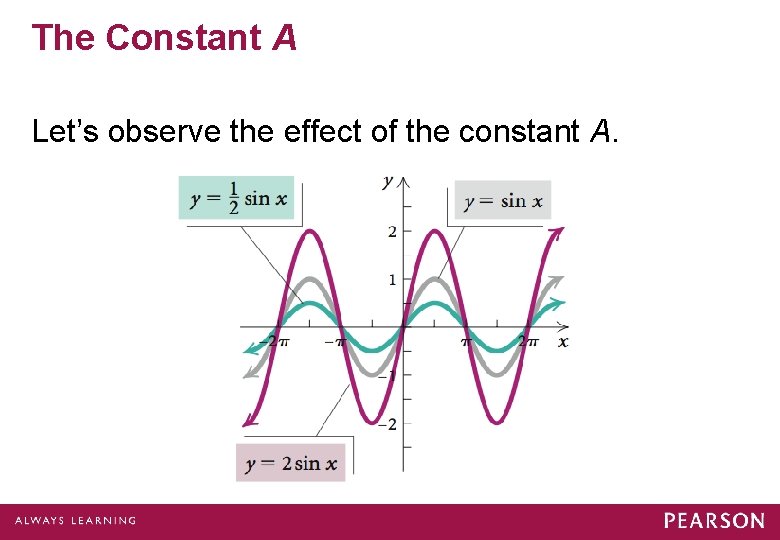
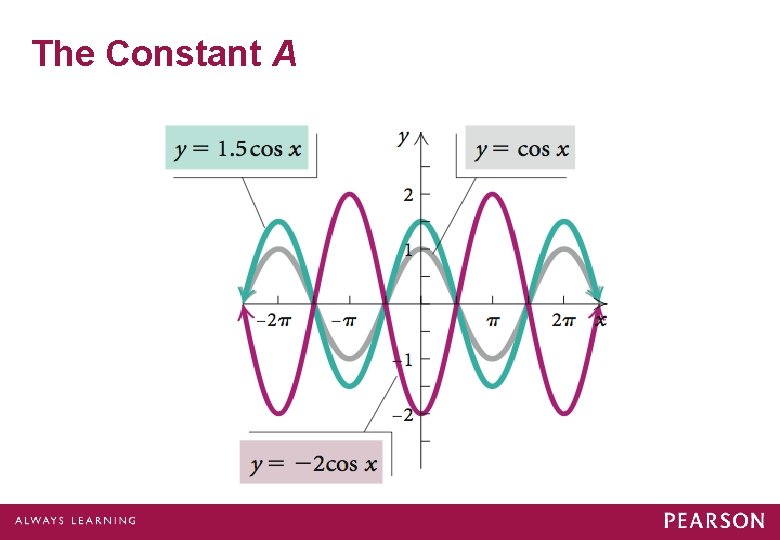
The Constant A Let’s observe the effect of the constant A.

The Constant A

The Constant A If |A| > 1, then there will be a vertical stretching. If |A| < 1, then there will be a vertical shrinking. If A < 0, the graph is also reflected across the x-axis.

Amplitude The amplitude of the graphs of y = A sin (Bx – C) + D and y = A cos (Bx – C) + D is |A|.

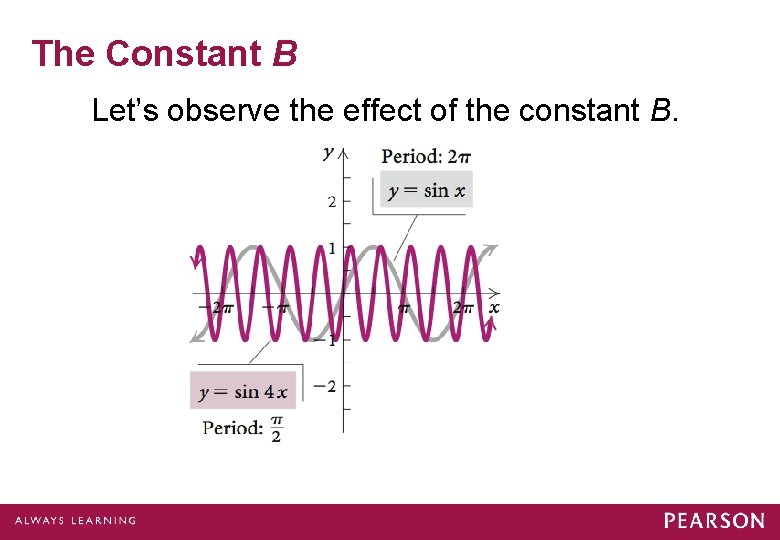
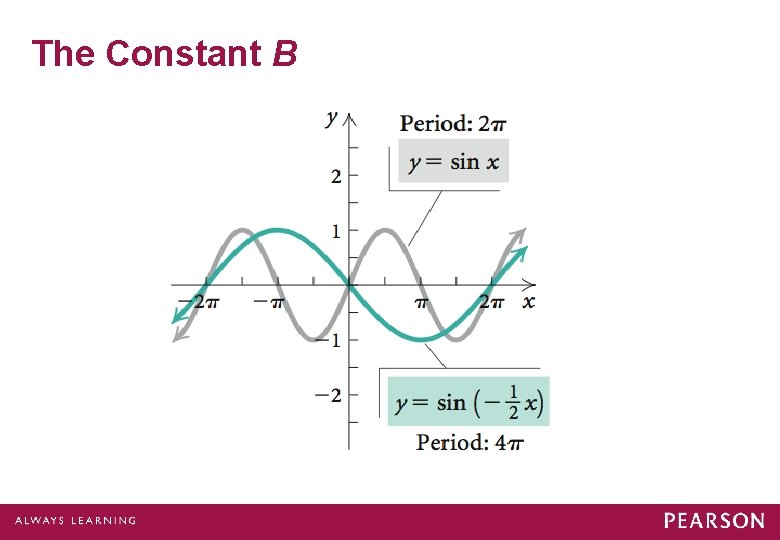
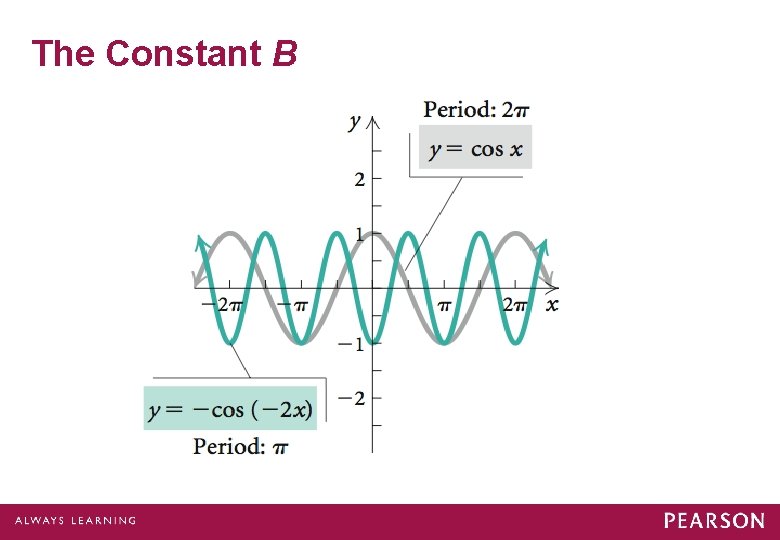
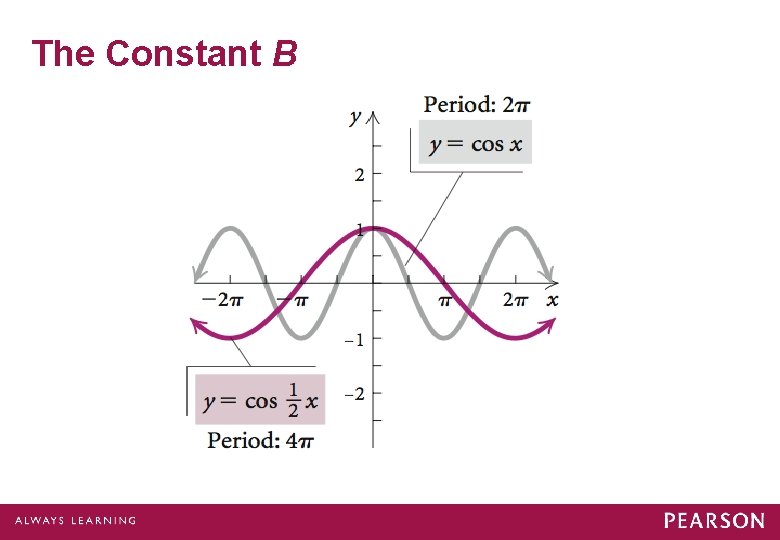
The Constant B Let’s observe the effect of the constant B.

The Constant B

The Constant B

The Constant B

The Constant B If |B| < 1, then there will be a horizontal stretching. If |B| > 1, then there will be a horizontal shrinking. If B < 0, the graph is also reflected across the y-axis.

Period The period of the graphs of y = A sin (Bx – C) + D and y = A cos (Bx – C) + D is

Period The period of the graphs of y = A csc (Bx – C) + D and y = A sec (Bx – C) + D is

Period The period of the graphs of y = A tan (Bx – C) + D and y = A cot (Bx – C) + D is

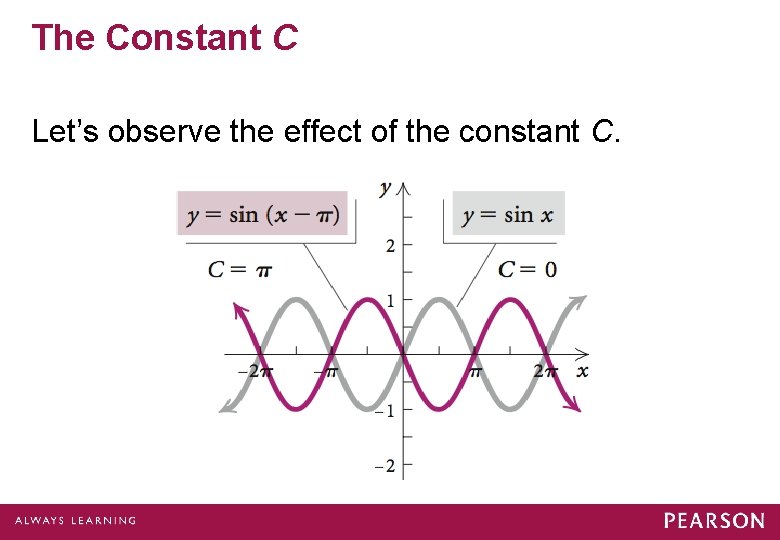
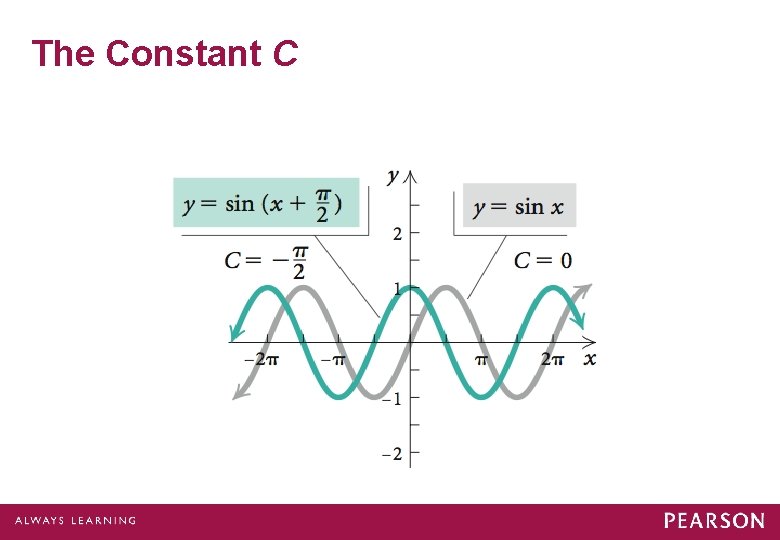
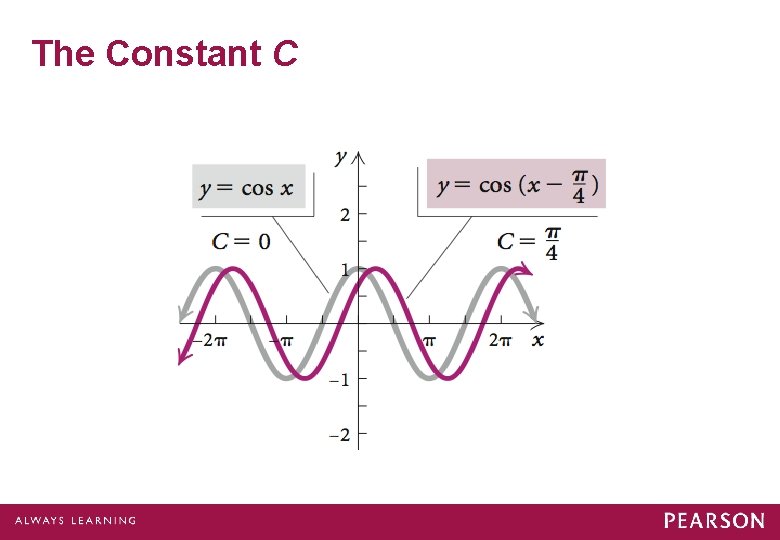
The Constant C Let’s observe the effect of the constant C.

The Constant C

The Constant C

The Constant C

The Constant C If B = 1, then if |C| < 0, then there will be a horizontal translation of |C| units to the right, and if |C| > 0, then there will be a horizontal translation of |C| units to the left.

Combined Transformations It is helpful to rewrite y = A sin (Bx – C) + D & as y = A cos (Bx – C) + D

Phase Shift The phase shift of the graphs and is the quantity

Phase Shift If C/B > 0, the graph is translated to the right |C/B| units. If C/B < 0, the graph is translated to the right |C/B| units.

Transformations of Sine and Cosine Functions To graph and follow the steps listed on the following slides.

Transformations of Sine and Cosine Functions 1. Stretch or shrink the graph horizontally according to B. |B| < 1 |B| > 1 B<0 Stretch horizontally Shrink horizontally Reflect across the y-axis The period is

Transformations of Sine and Cosine Functions 2. Stretch or shrink the graph vertically according to A. |A| < 1 |A| > 1 A<0 Shrink vertically Stretch vertically Reflect across the x-axis The amplitude is A.

Transformations of Sine and Cosine Functions 3. Translate the graph horizontally according to C/B. The phase shift is

Transformations of Sine and Cosine Functions 4. Translate the graph vertically according to D. D<0 |D| units down D>0 D units up

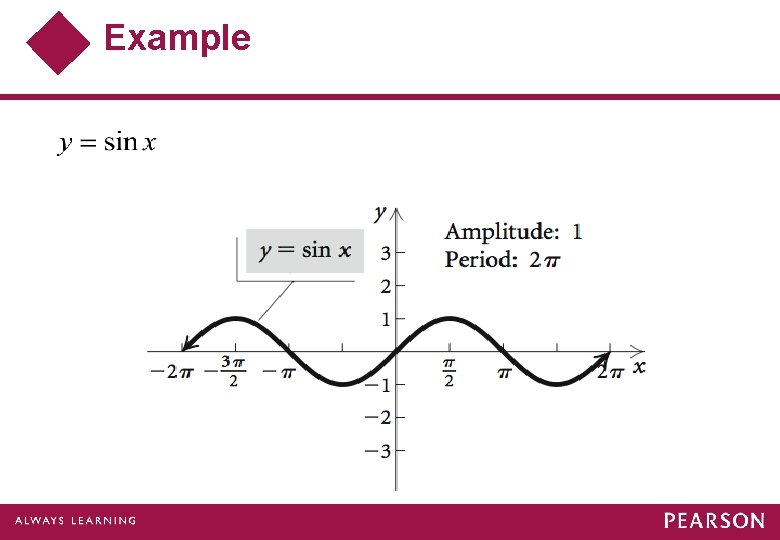
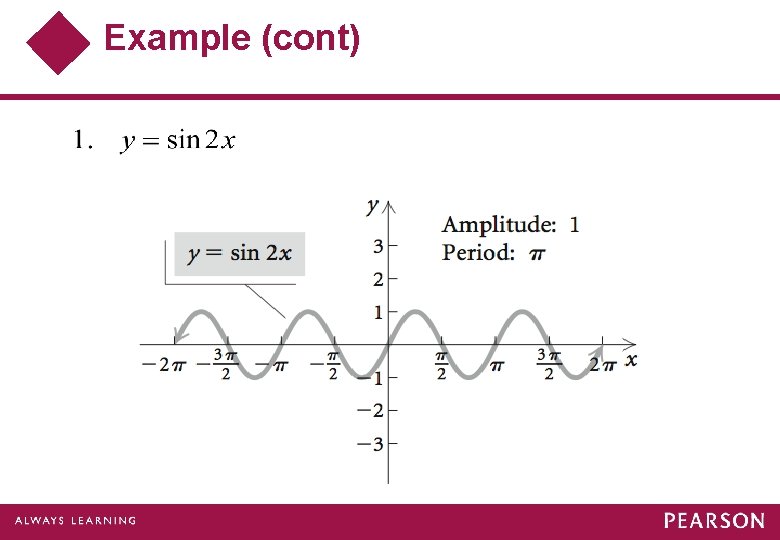
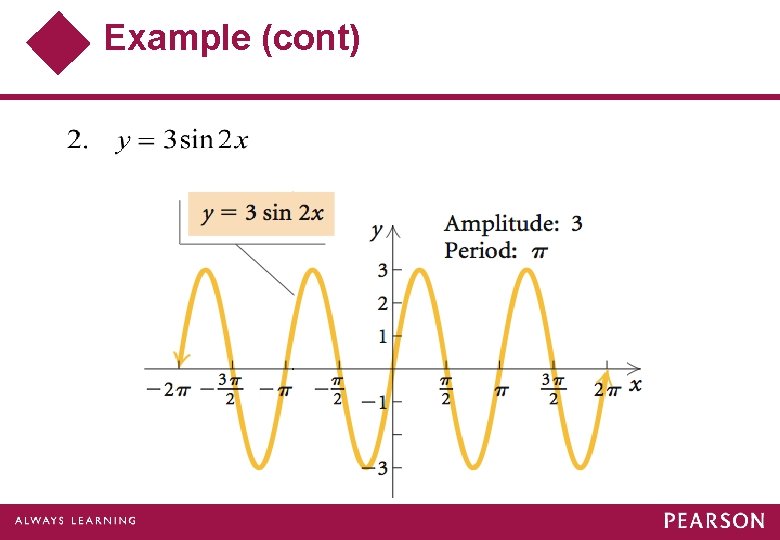
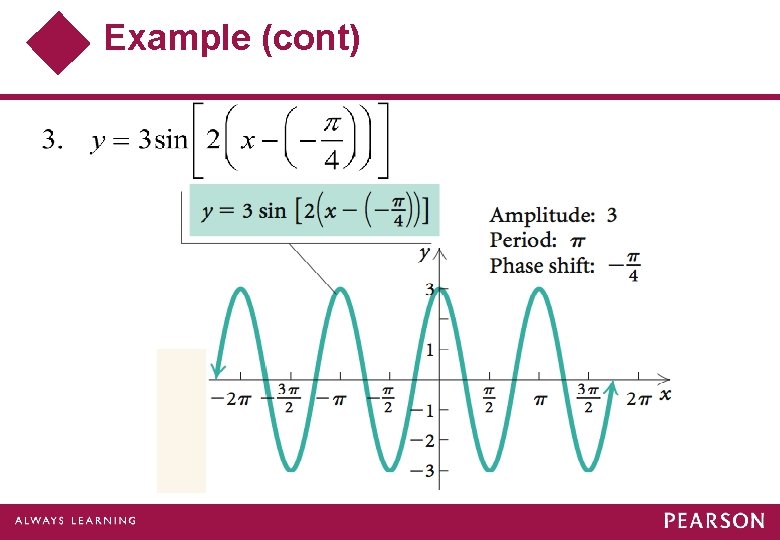
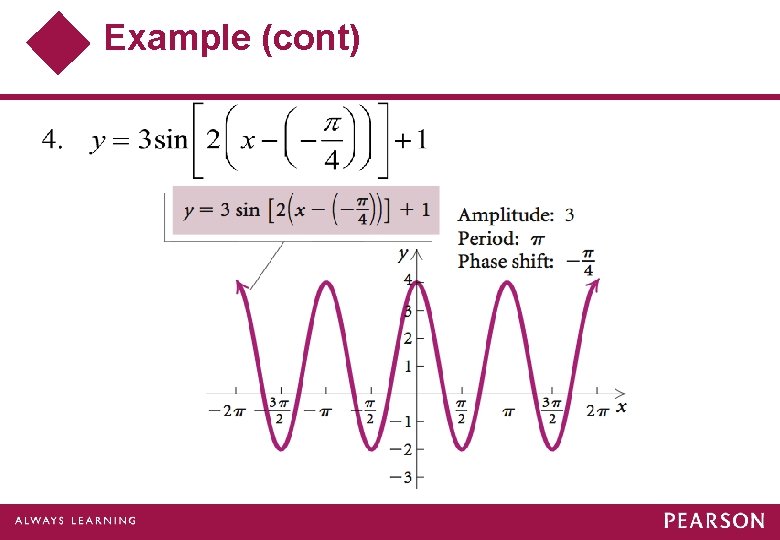
Example Sketch the graph of Find the amplitude, the period, and the phase shift. Solution:

Example (cont) To create the final graph, we begin with the basic sine curve, y = sin x. Then we sketch graphs of each of the following equations in sequence.

Example

Example (cont)

Example (cont)

Example (cont)

Example (cont)

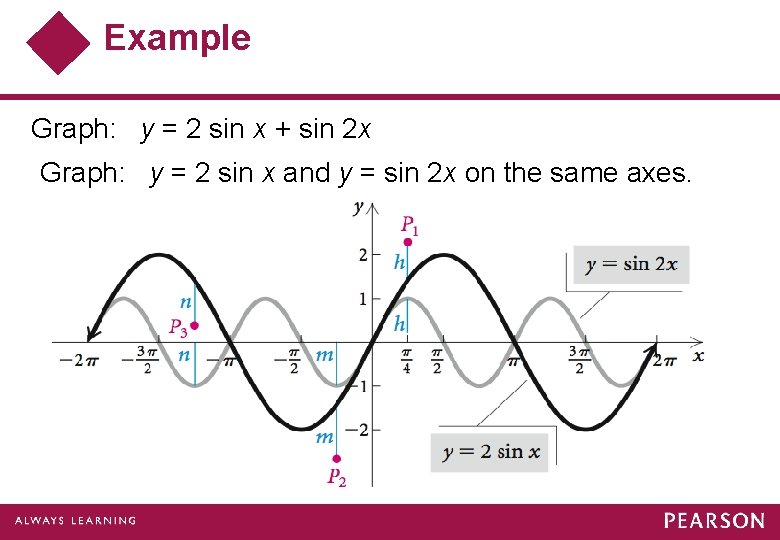
Example Graph: y = 2 sin x + sin 2 x Graph: y = 2 sin x and y = sin 2 x on the same axes.

Example (cont) Graphically add some y-coordinates, or ordinates, to obtain points on the graph that we seek. At x = π/4, transfer h up to add it to 2 sin x, yielding P 1. At x = – π/4, transfer m down to add it to 2 sin x, yielding P 2. At x = – 5π/4, add the negative ordinate of sin 2 x to the positive ordinate of 2 sin x, yielding P 3. This method is called addition of ordinates, because we add the y-values (ordinates) of y = sin 2 x to the y-values (ordinates) of y = 2 sin x.

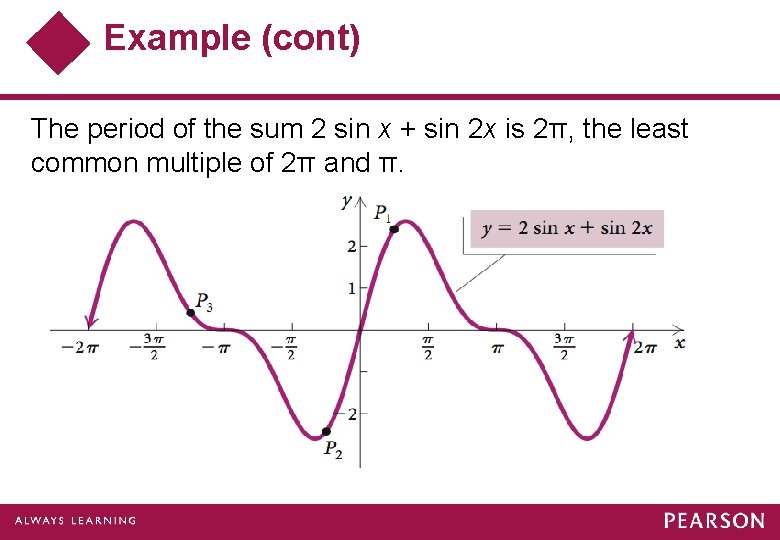
Example (cont) The period of the sum 2 sin x + sin 2 x is 2π, the least common multiple of 2π and π.

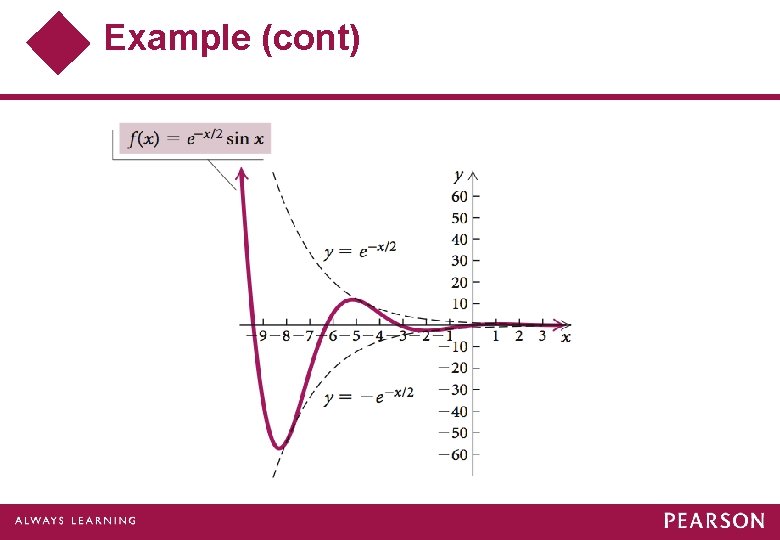
Example Sketch a graph of Solution f is the product of two functions g and h, where To find the function values, we can multiply ordinates. Start with The graph crosses the x-axis at values of x for which sin x = 0, kπ for integer values of k.

Example (cont) f is constrained between the graphs of y = –e–x/2 and y = e–x/2. Start by graphing these functions using dashed lines. Since f(x) = 0 when x = kπ, k an integer, we mark those points on the graph. Use a calculator to compute other function values. The graph is on the next slide.

Example (cont)