Sec 3 1 Introduction to Linear System Sec

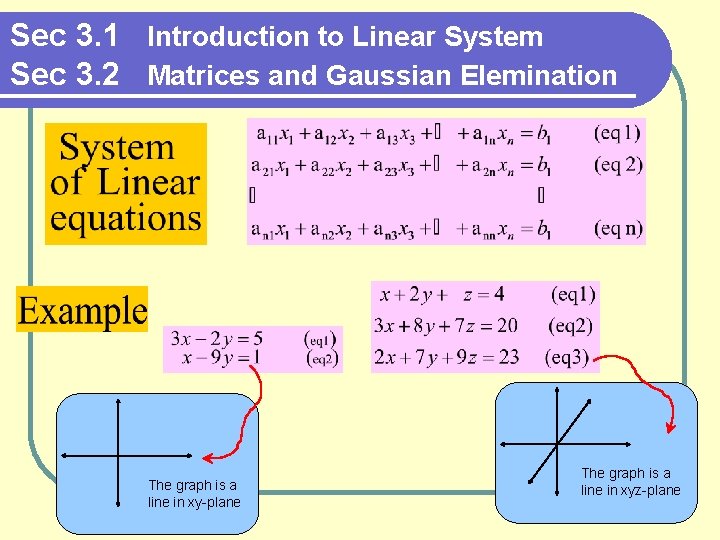
Sec 3. 1 Introduction to Linear System Sec 3. 2 Matrices and Gaussian Elemination The graph is a line in xy-plane The graph is a line in xyz-plane

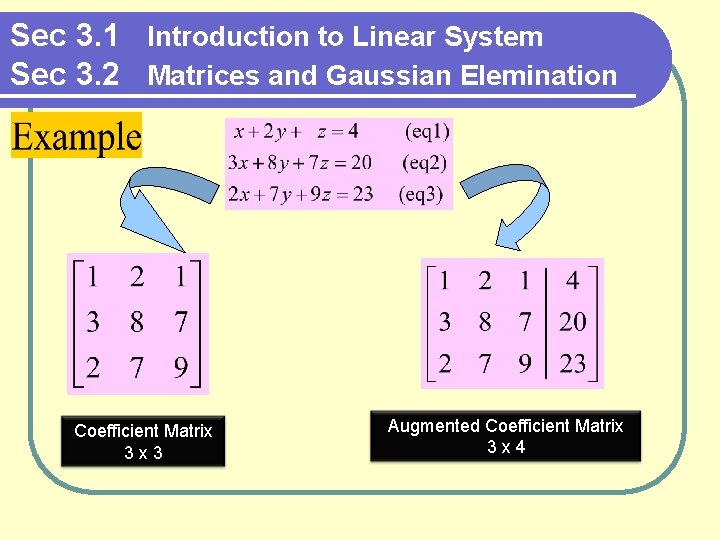
Sec 3. 1 Introduction to Linear System Sec 3. 2 Matrices and Gaussian Elemination Coefficient Matrix 3 x 3 Augmented Coefficient Matrix 3 x 4

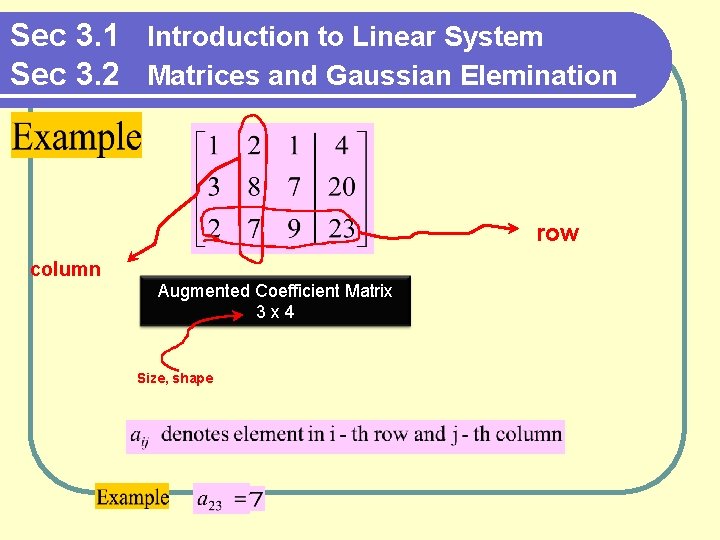
Sec 3. 1 Introduction to Linear System Sec 3. 2 Matrices and Gaussian Elemination row column Augmented Coefficient Matrix 3 x 4 Size, shape

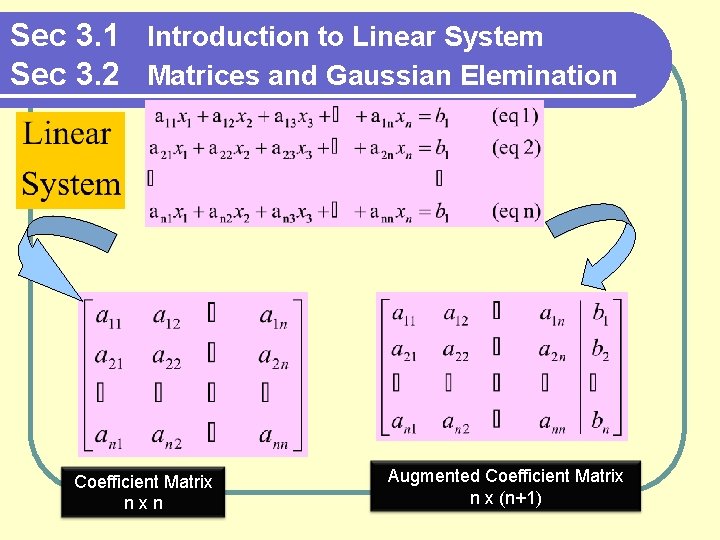
Sec 3. 1 Introduction to Linear System Sec 3. 2 Matrices and Gaussian Elemination Coefficient Matrix nxn Augmented Coefficient Matrix n x (n+1)

Sec 3. 1 Introduction to Linear System Sec 3. 2 Matrices and Gaussian Elemination

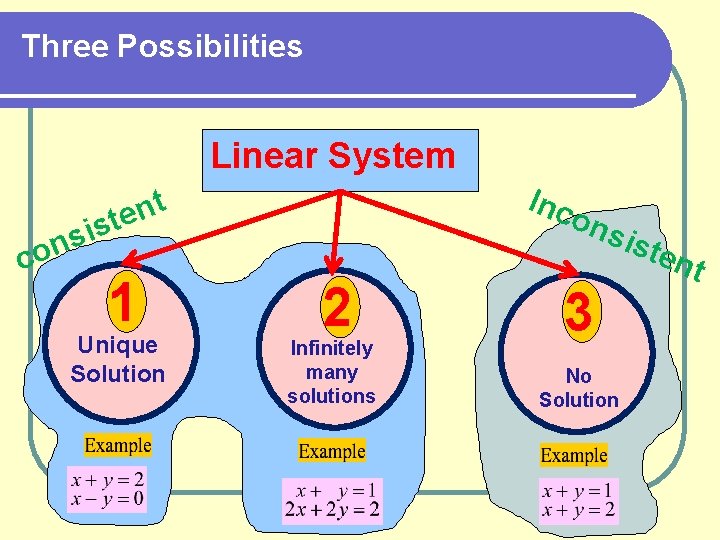
Three Possibilities Linear System Inc t n e t sis con 1 Unique Solution 2 Infinitely many solutions 3 No Solution iste nt

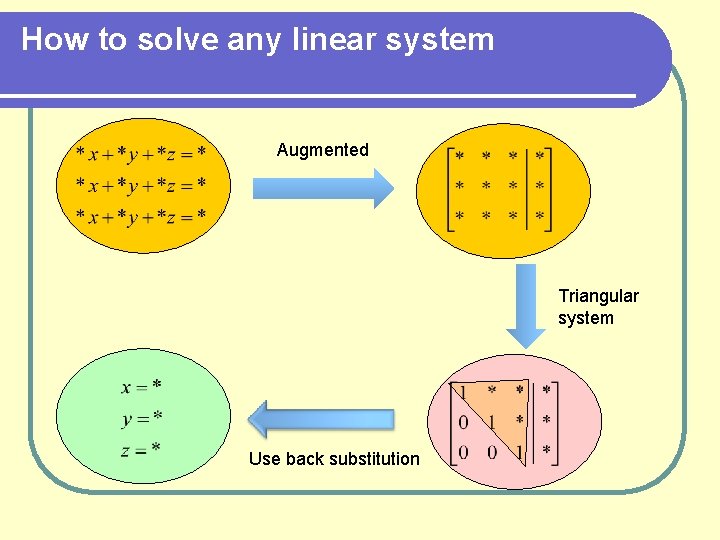
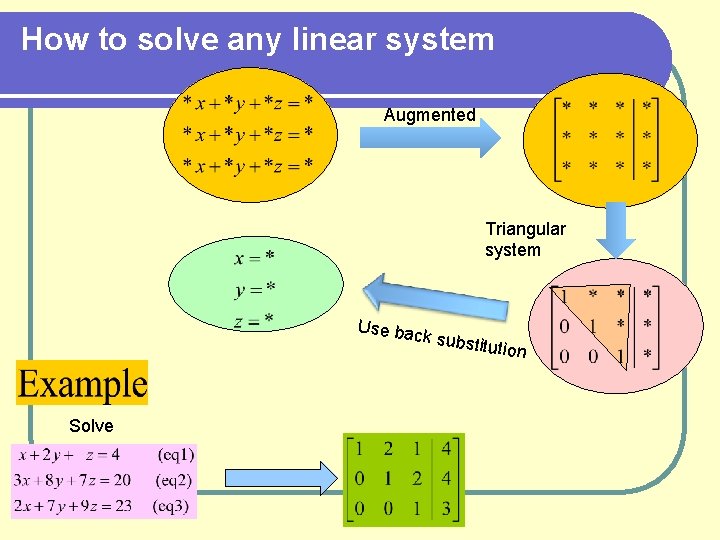
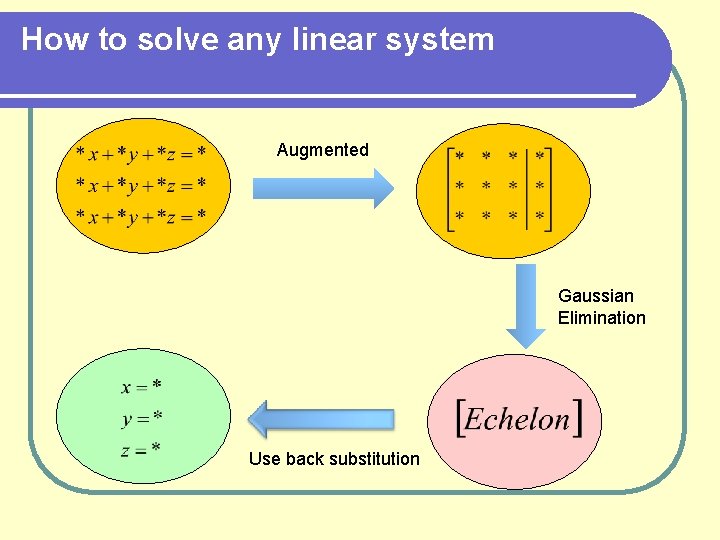
How to solve any linear system Augmented Triangular system Use back substitution

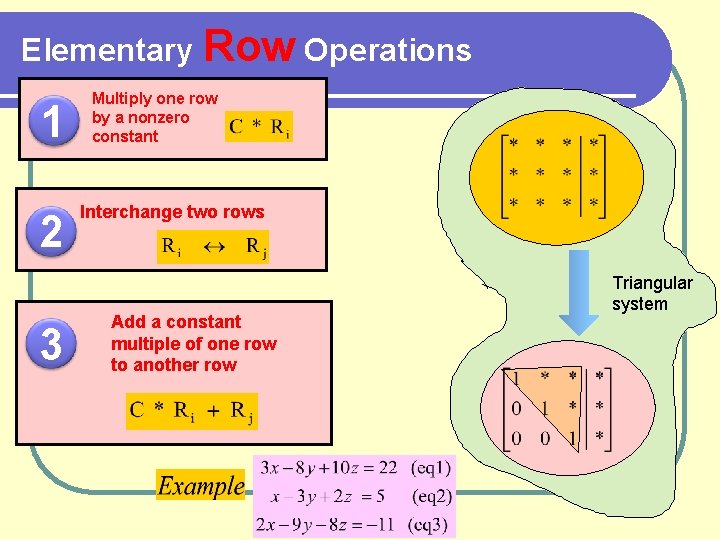
Elementary Row Operations 1 2 3 Multiply one row by a nonzero constant Interchange two rows Add a constant multiple of one row to another row Triangular system

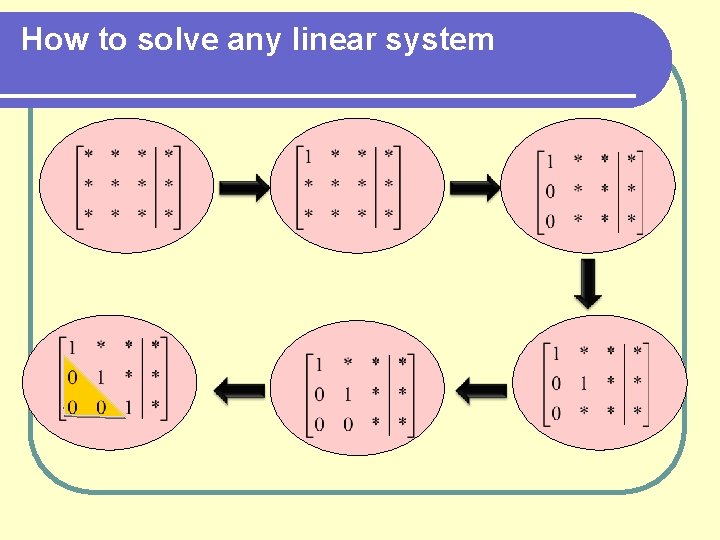
How to solve any linear system

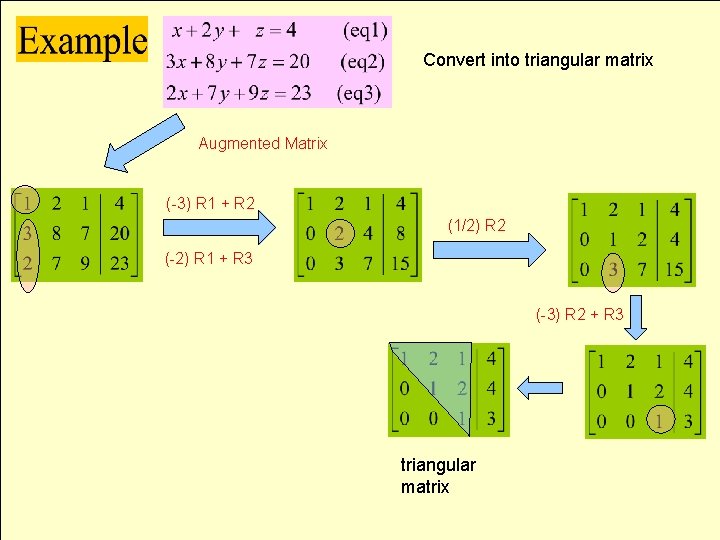
Convert into triangular matrix Augmented Matrix (-3) R 1 + R 2 (1/2) R 2 (-2) R 1 + R 3 (-3) R 2 + R 3 triangular matrix

Convert into triangular matrix

How to solve any linear system Augmented Triangular system Use bac k substi Solve tution

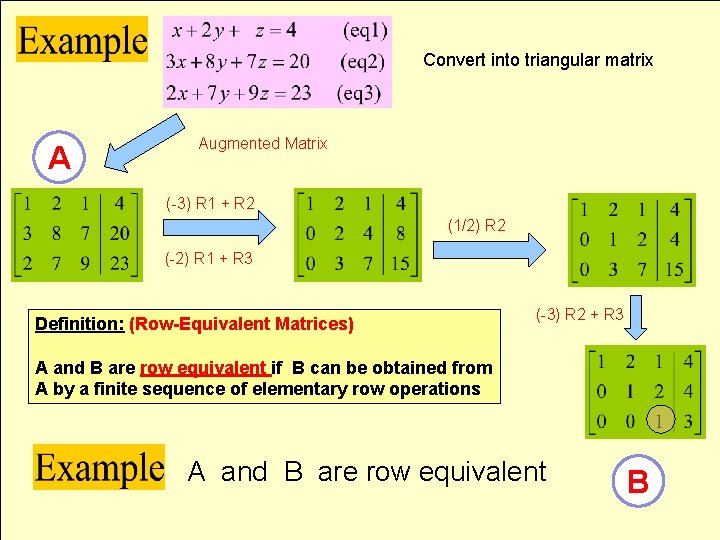
Convert into triangular matrix A Augmented Matrix (-3) R 1 + R 2 (1/2) R 2 (-2) R 1 + R 3 Definition: (Row-Equivalent Matrices) (-3) R 2 + R 3 A and B are row equivalent if B can be obtained from A by a finite sequence of elementary row operations A and B are row equivalent B

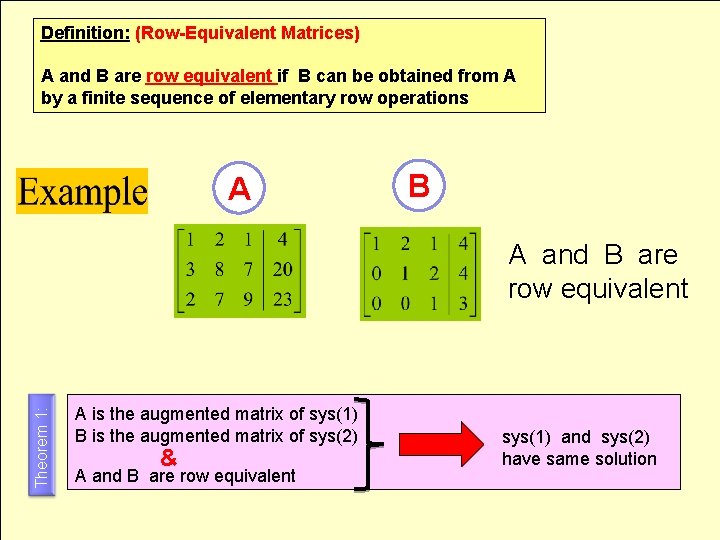
Definition: (Row-Equivalent Matrices) A and B are row equivalent if B can be obtained from A by a finite sequence of elementary row operations A B Theorem 1: A and B are row equivalent A is the augmented matrix of sys(1) B is the augmented matrix of sys(2) & A and B are row equivalent sys(1) and sys(2) have same solution

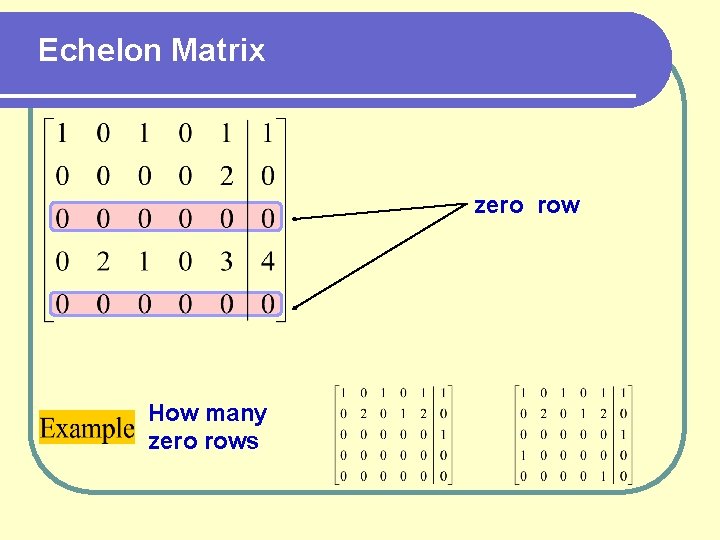
Echelon Matrix zero row How many zero rows

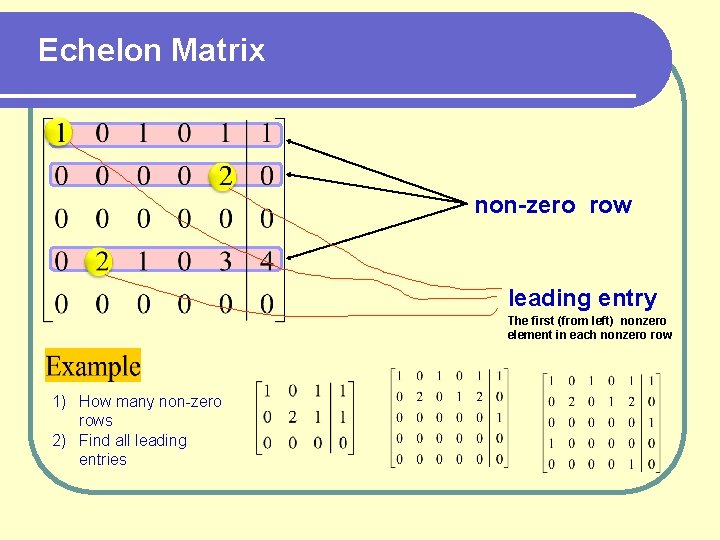
Echelon Matrix non-zero row leading entry The first (from left) nonzero element in each nonzero row 1) How many non-zero rows 2) Find all leading entries

Echelon Matrix Def: A matrix A in row-echelon form if 1) All zero rows are at the bottom of the matrix 2) In consecutive nonzero rows the leading in the lower row appears to the right of the leading in the higher row

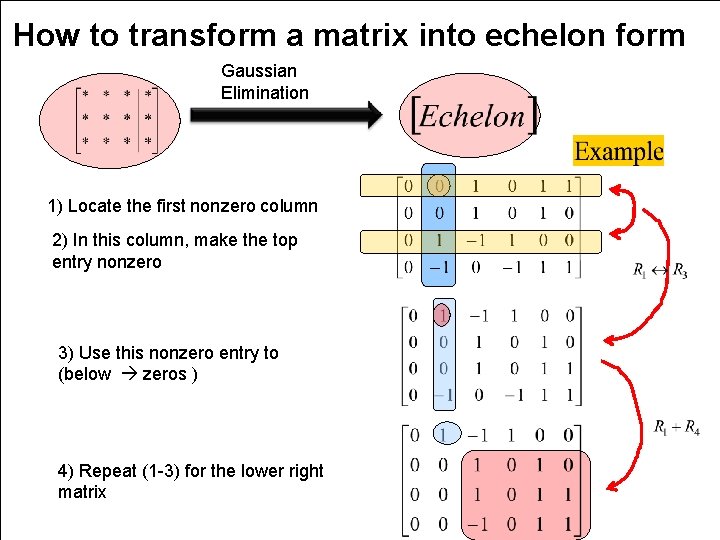
How to transform a matrix into echelon form Gaussian Elimination 1) Locate the first nonzero column 2) In this column, make the top entry nonzero 3) Use this nonzero entry to (below zeros ) 4) Repeat (1 -3) for the lower right matrix

Echelon Matrix Reduce the augmented matrix to echelon form.

How to solve any linear system Augmented Gaussian Elimination Use back substitution

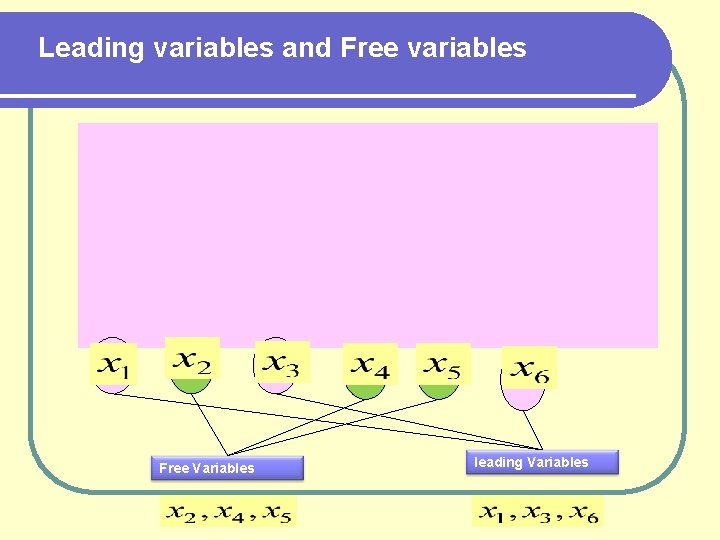
Leading variables and Free variables Free Variables leading Variables

Back Substitution 1) Set each free variable to parameter ( s, t, …) 2) Solve for the leading variables. Start from last row. Second row gives: first row gives: Thus the system has an infinite solution set consisting of all (x, y, z) given in terms of the parameter s as follows

Back Substitution The linear systems are in echelon form, solve each by back substitution 23

Quiz #1 on Saturday Sec 3. 1 + Sec 3. 2 24