Searching and Sorting Page 1 Searching and Sorting

Searching and Sorting Page 1 Searching and Sorting Chapter 9 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

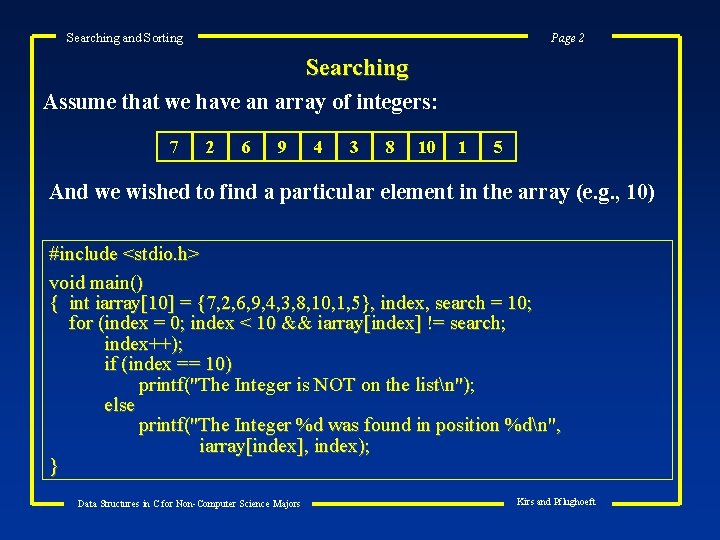
Searching and Sorting Page 2 Searching Assume that we have an array of integers: 7 2 6 9 4 3 8 10 1 5 And we wished to find a particular element in the array (e. g. , 10) #include <stdio. h> void main() { int iarray[10] = {7, 2, 6, 9, 4, 3, 8, 10, 1, 5}, index, search = 10; for (index = 0; index < 10 && iarray[index] != search; index++); if (index == 10) printf("The Integer is NOT on the listn"); else printf("The Integer %d was found in position %dn", iarray[index], index); } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 3 Following the program during the for loop: for (index = 0; index < 10 && iarray[index] != search; index++); Variable values (search set to 10) Condition Check: index iarray[index] index < 10 && iarray[index] != search; 0 7 TRUE 1 2 TRUE 6 TRUE 2 9 TRUE 3 4 4 TRUE 5 3 TRUE 6 8 TRUE 7 10 FALSE Exit Loop printf("The Integer %d was found in position %dn", iarray[index], index); The Integer 10 was found in position 7 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 4 Since the list of integers is not in any order, we must perform a sequential search: • • • Each element in the list be checked until: • The element is found • The end of the list is reached The procedure is adequate if each element is to be considered (e. g. , in a transaction listing) The procedure is inadequate if specific elements are sought In a sequential search: • The MAXIMUM number of searches required is: (where n = the number of elements on the list) • The AVERAGE number of searches required is: Data Structures in C for Non-Computer Science Majors n+1 (n + 1)/2 Kirs and Pflughoeft

Searching and Sorting Page 5 The number of searches required is dependent upon the number of elements in the list: Number elements Maximum Searches (n + 1) Average Searches (n + 1)/2 10 100 1, 000 100, 000 1, 000, 000 11 101 1, 001 100, 001 1, 000, 001 5. 5 550. 5 5, 000. 5 500, 000. 5 5, 000, 000. 5 500, 000. 5 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 6 IF the list were sorted 1 2 3 4 5 6 7 8 9 10 We could perform a Binary Search on it: 1. 2. 3. 4. 5. Determine the bottom and top of the list If the bottom offset > top offset: STOP The number is NOT in the list Find the midpoint = (bottom + top)/2 If the element at the midpoint is the Search number: STOP The number has been found If the element is greater than the search number: top = midpoint - 1 Else (the element is less than the search number): bottom = midpoint + 1 Go to step 2 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

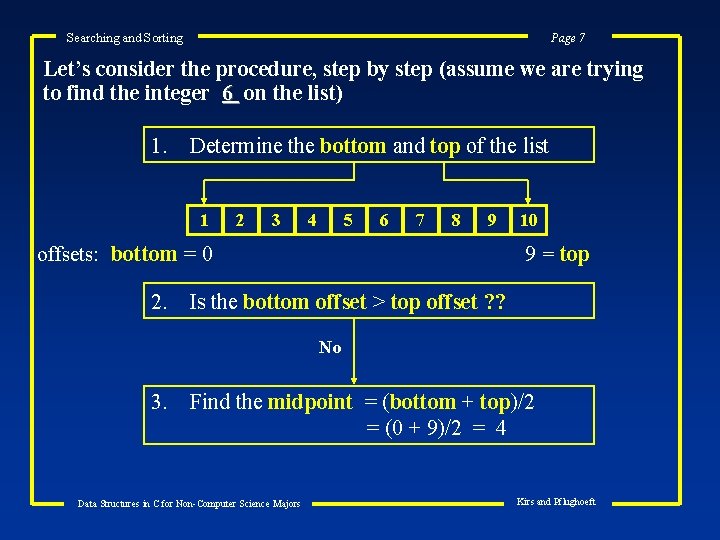
Searching and Sorting Page 7 Let’s consider the procedure, step by step (assume we are trying to find the integer 6 on the list) 1. Determine the bottom and top of the list 1 2 3 4 5 6 7 8 9 offsets: bottom = 0 2. 10 9 = top Is the bottom offset > top offset ? ? No 3. Find the midpoint = (bottom + top)/2 = (0 + 9)/2 = 4 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

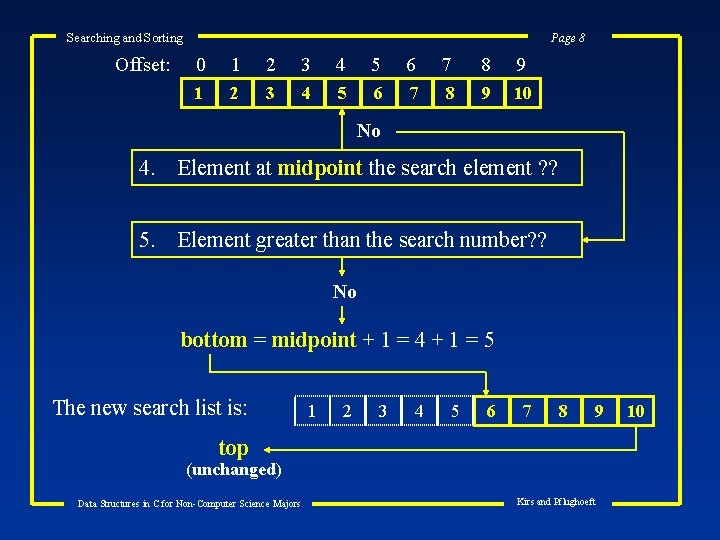
Searching and Sorting Offset: Page 8 0 1 2 3 4 5 6 7 8 9 10 No 4. Element at midpoint the search element ? ? 5. Element greater than the search number? ? No bottom = midpoint + 1 = 4 + 1 = 5 The new search list is: 1 2 3 4 5 6 7 8 9 top (unchanged) Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft 10

Searching and Sorting Offset: Page 9 0 1 2 3 4 5 6 7 8 9 10 bottom = 5 2. 9 = top Is the bottom offset > top offset ? ? No 3. Offset: Find the midpoint = (bottom + top)/2 = (5 + 9)/2 = 7 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Offset: Page 10 0 1 2 3 4 5 6 7 8 9 10 No 4. Element at midpoint the search element ? ? 5. Element greater than the search number? ? Yes top = midpoint - 1 = 7 - 1 = 6 The new search list is: 1 2 3 4 5 6 7 8 9 bottom (unchanged) Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft 10

Searching and Sorting Offset: Page 11 0 1 2 3 4 5 5 6 6 7 bottom = 5 2. 7 8 8 9 9 10 6 = top Is the bottom offset > top offset ? ? No 3. Offset: Find the midpoint = (bottom + top)/2 = (5 + 6)/2 = 5 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Offset: Page 12 0 1 2 3 4 5 6 7 8 9 10 bottom = 5 = top 2. Is the bottom offset > top offset ? ? No 3. Offset: Find the midpoint = (bottom + top)/2 = (5 + 5)/2 = 5 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Offset: Page 13 0 1 2 3 4 5 6 7 8 9 10 Yes: STOP 4. Element at midpoint the search element ? ? The search number was found This does NOT seem like a savings over a sequential search. In fact, it seems like much more work. In this case (because the list is short (and because we intentionally chose the worst case scenario), probably not. Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

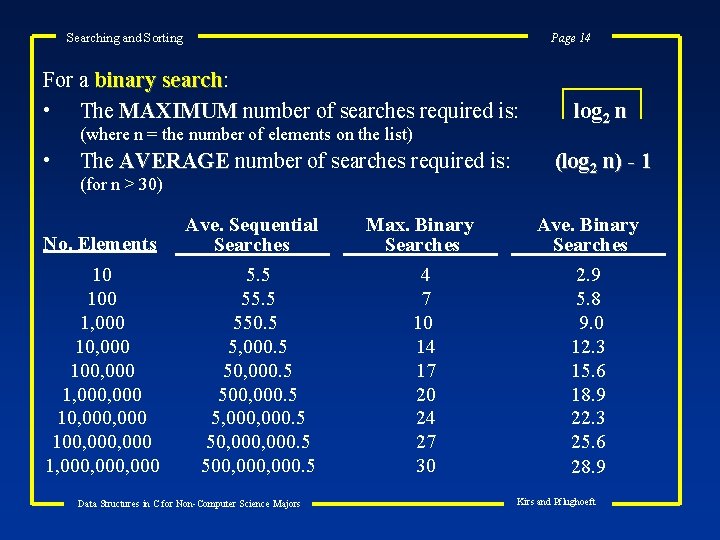
Searching and Sorting Page 14 For a binary search: search • The MAXIMUM number of searches required is: (where n = the number of elements on the list) • The AVERAGE number of searches required is: (for n > 30) No. Elements Ave. Sequential Searches 10 100 1, 000 100, 000 1, 000, 000 5. 5 550. 5 5, 000. 5 500, 000. 5 5, 000, 000. 5 500, 000. 5 Data Structures in C for Non-Computer Science Majors log 2 n (log 2 n) - 1 Max. Binary Searches Ave. Binary Searches 4 7 10 14 17 20 24 27 30 2. 9 5. 8 9. 0 12. 3 15. 6 18. 9 22. 3 25. 6 28. 9 Kirs and Pflughoeft

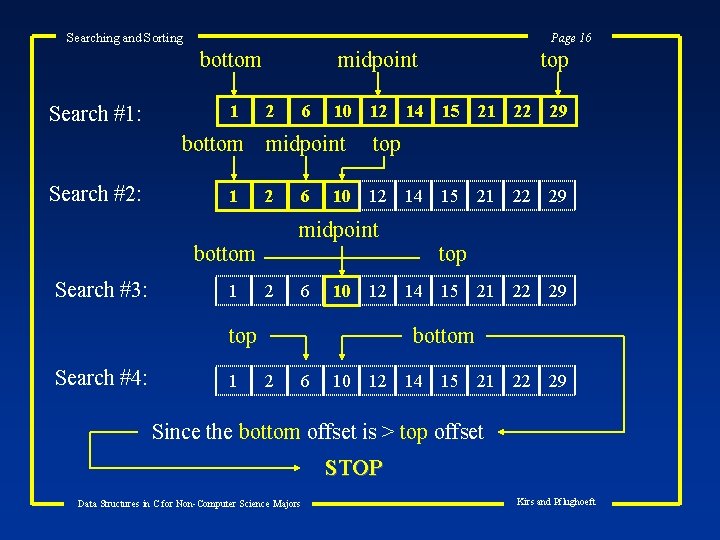
Searching and Sorting Page 15 Is a binary search always preferred to a sequential search? NO. It depends: • If all elements are to be examined, a sequential search is preferred • A binary search: • Is programatically more complex • requires more comparisons • As a general rule of thumb, a binary search is preferred if the list contains more than 30 -50 elements How does a binary search work if an element is NOT on the list? ? Consider the array: 1 2 6 10 12 14 15 21 22 29 Suppose we were to search the list for the value 9 (Which is NOT on the list) Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 16 bottom Search #1: 1 bottom Search #2: 1 midpoint 2 1 10 12 midpoint top 2 12 6 10 12 top Search #4: 1 14 15 21 22 29 midpoint bottom Search #3: 6 top 14 15 21 bottom 2 6 10 12 14 15 21 Since the bottom offset is > top offset STOP Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 17 What would the C code for a binary search look like? ? #include <stdio. h> #include <stdlib. h> void main() { int iarray[10] = {1, 2, 6, 10, 12, 14, 15, 21, 22, 29}, search, bottom = 0, top = 9, found = 0, midpt = 9/2; char temp[10]; printf("n. Enter the number to search for: "); search = atoi(gets(temp)); while ((top > bottom) && (found == 0)) if (iarray[midpt] == search) found = 1; else { if (search > iarray[midpt]) bottom = midpt + 1; else top = midpt - 1; midpt = (bottom + top)/2; } if (found == 0) printf("The Integer is NOT on the listn"); else printf("The Integer %d was found in position %dn", iarray[midpt], midpt); } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 18 Sorting Why? • Displaying in order • Faster Searching Categories • Internal – List elements manipulated in RAM – Faster – Limited by amount of RAM • External – External (secondary) storage areas used – Slower – Used for Larger Lists – Limited by secondary storage (Disk Space) Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 19 Basic Internal Sort Types • Exchange (e. g. , bubble sort) – Single list – Incorrectly ordered pairs swapped as found • Selection – Two lists (generally); Selection with exchange uses one list – Largest/Smallest selected in each pass and moved into position • Insertion – One or two lists (two more common) – Each item from original list inserted into the correct position in the new list Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 20 Exchange Sorts Bubble Sort 1: The largest element ‘bubbles’ up Given: 7 2 6 1 3 4 8 10 9 5 • Point to bottom element • Compare with element above: above • if the element is greater, swap positions (in this case, swap) • if the element is smaller, reset the bottom pointer (not here) • Continue the process until the largest element is at the end • This will require n-1 comparisons (9 for our example) (where n = the length of the unsorted list) • At the end of the pass: • The largest number is in the last position • The length of the unsorted list has been shortened by 1 Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 21 How does this work? ? Comparison: 1 Pass #1: 7 2 1 6 3 4 8 10 9 5 10 9 5 Swap 2 2 7 6 1 Swap 3 2 6 7 1 3 Swap 4 2 6 1 7 3 4 Swap 5 2 6 1 3 7 4 8 Swap 6 2 6 1 3 4 7 8 10 Don’t Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 22 Continuing Comparison: 7 Pass #1: 2 6 1 3 4 7 8 10 9 5 Don’t Swap 8 2 6 1 3 4 7 8 10 9 5 Swap 9 2 6 1 3 4 7 8 9 10 5 Swap The new list appears as 2 6 1 3 4 7 8 9 5 10 Note: • 9 (n - 1) comparisons were required • We know that the largest element is at the end of the list Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Continuing Comparison: 1 (10) Page 23 2 6 1 Pass #2: 3 4 7 8 9 5 10 9 5 10 Don’t’ Swap 2 (11) 2 6 1 3 4 Swap 3 (12) 2 1 6 3 4 Swap 4 (13) 2 1 3 6 4 7 Swap 5 (14) 2 1 3 4 6 7 8 Don’t Swap 6 (15) 2 1 3 4 6 7 8 9 5 10 Don’t Swap 7 (16) 2 1 3 4 6 7 8 9 5 10 Don’t Swap 8 (17) 2 1 3 4 6 7 8 9 5 10 Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Continuing Comparison: 1 (18) Page 24 2 1 3 Pass #3: 4 6 7 8 5 9 10 9 10 Swap 2 (19) 1 2 3 4 6 7 Don’t Swap 3 (20) 1 2 3 4 6 7 Don’t Swap 4 (21) 1 2 3 4 6 7 8 Don’t Swap 5 (22) 1 2 3 4 6 7 8 5 Don’t Swap 6 (23) 1 2 3 4 6 7 8 5 9 10 Don’t Swap 7 (24) 1 2 3 4 6 7 8 5 9 10 Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Continuing Comparison: 1 (25) Page 25 Pass #4: 1 2 3 4 6 7 5 8 9 10 9 10 Don’t Swap 2 (26) 1 2 3 4 6 Don’t Swap 3 (27) 1 2 3 4 6 7 Don’t Swap 4 (28) 1 2 3 4 6 7 5 Don’t Swap 5 (29) 1 2 3 4 6 7 5 8 Don’t Swap 6 (30) 1 2 3 4 6 7 5 8 9 10 Don’t Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Continuing Comparison: 1 (31) Page 26 1 2 3 Pass #5: 4 6 5 7 8 9 10 9 10 Don’t Swap 2 (32) 1 2 3 4 6 5 Don’t Swap 3 (33) 1 2 3 4 6 5 Don’t Swap 4 (34) 1 2 3 4 6 5 7 Don’t Swap 5 (35) 1 2 3 4 6 5 7 8 Swap 1 2 3 4 5 6 7 8 And the new list Is in order, so we can stop. Right ? ? ? Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 27 NO. In the WORST case scenario (numbers in reverse order): 10 9 8 7 6 5 4 A bubble sort would yield: After Pass Order Pass 9 8 7 6 5 4 3 1 2 8 7 6 5 4 3 2 3 7 6 5 4 3 2 1 4 6 5 4 3 2 1 7 5 4 3 2 1 6 7 5 4 3 2 1 5 6 7 6 3 2 1 4 5 6 7 7 8 9 2 1 1 2 3 3 4 4 5 5 6 6 7 7 3 1 2 1 10 1 8 8 9 9 9 10 10 10 8 8 8 9 9 9 10 10 10 Maximum Comparisons necessary Data Structures in C for Non-Computer Science Majors 2 Comparisons 9 8 7 6 5 4 3 2 1 45 Kirs and Pflughoeft

Searching and Sorting Page 28 What does this imply ? ? ? If we want to be sure, given an array of n dimensions, we need a maximum of n-1 passes to sort the array, and a total of: S [(n-1)+(n-2)+. . . +1] or (n 2 - n)/2 comparisons. No. Items 10 100 1, 000 100, 000 1, 000 Max. Passes: (n - 1) 9 99 9, 999 999, 999 Max. Compares: (n 2 - n)/2 45 4, 950 499, 500 49, 995, 000 4, 999, 950, 000 499, 999, 500, 000 The C code necessary? Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

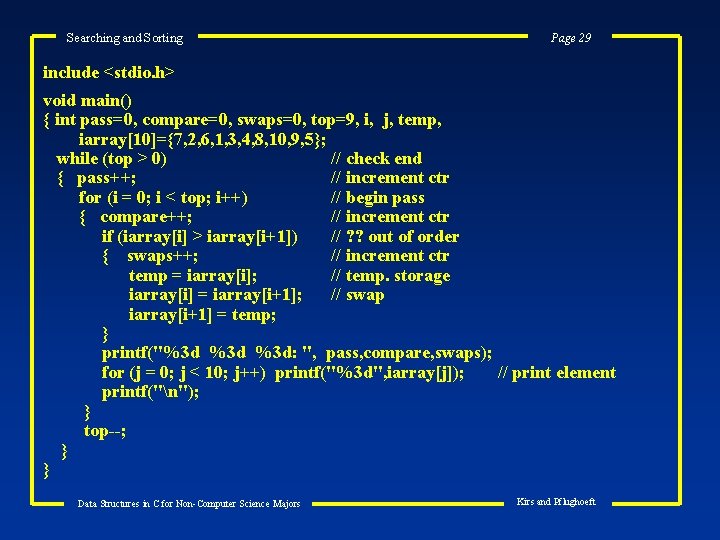
Searching and Sorting Page 29 include <stdio. h> void main() { int pass=0, compare=0, swaps=0, top=9, i, j, temp, iarray[10]={7, 2, 6, 1, 3, 4, 8, 10, 9, 5}; while (top > 0) // check end { pass++; // increment ctr for (i = 0; i < top; i++) // begin pass { compare++; // increment ctr if (iarray[i] > iarray[i+1]) // ? ? out of order { swaps++; // increment ctr temp = iarray[i]; // temp. storage iarray[i] = iarray[i+1]; // swap iarray[i+1] = temp; } printf("%3 d %3 d: ", pass, compare, swaps); for (j = 0; j < 10; j++) printf("%3 d", iarray[j]); // print element printf("n"); } top--; } } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

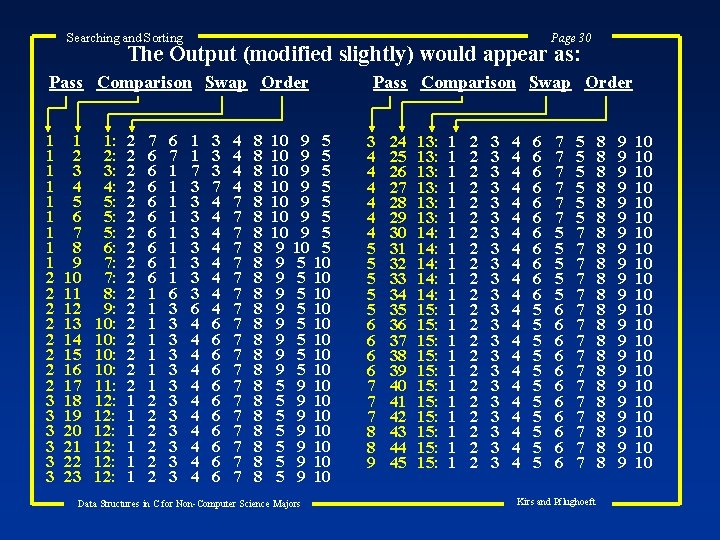
Searching and Sorting Page 30 The Output (modified slightly) would appear as: Pass Comparison Swap Order 1 1 1 1 1 2 2 2 2 3 3 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1: 2: 3: 4: 5: 5: 5: 6: 7: 7: 8: 9: 10: 10: 11: 12: 12: 12: 2 2 2 2 2 1 1 1 7 6 6 6 6 6 1 1 1 1 2 2 2 6 7 1 1 1 1 6 3 3 3 1 1 7 3 3 3 3 6 4 4 4 3 3 3 7 4 4 4 4 6 6 6 4 4 7 7 7 7 7 8 8 8 8 8 8 10 9 5 10 9 5 9 10 5 9 5 10 9 5 10 5 9 10 5 9 10 Data Structures in C for Non-Computer Science Majors Pass Comparison Swap Order 3 4 4 4 5 5 5 6 6 7 7 7 8 8 9 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 13: 13: 13: 14: 14: 14: 15: 15: 15: 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4 6 6 6 5 5 5 7 7 7 5 5 5 6 6 6 5 5 5 7 7 7 7 Kirs and Pflughoeft 8 8 8 8 8 8 9 9 9 9 9 9 10 10 10 10 10 10

Searching and Sorting Page 31 Since the list IS sorted after 5 passes (35 comparisons), why can’t we stop? ? We could, IF we knew the list was sorted: • If we make a pass without swapping any elements, we know the list is sorted (one extra pass is needed) • We need a flag which we set to 0 (zero) before each pass: • If we make any swaps in the pass, we set the flag to 1 • If we exit the loop, and the flag = 0, 0 the list is sorted For our example, we could stop after Pass 6 (39 comparisons) How would the C code appear? Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

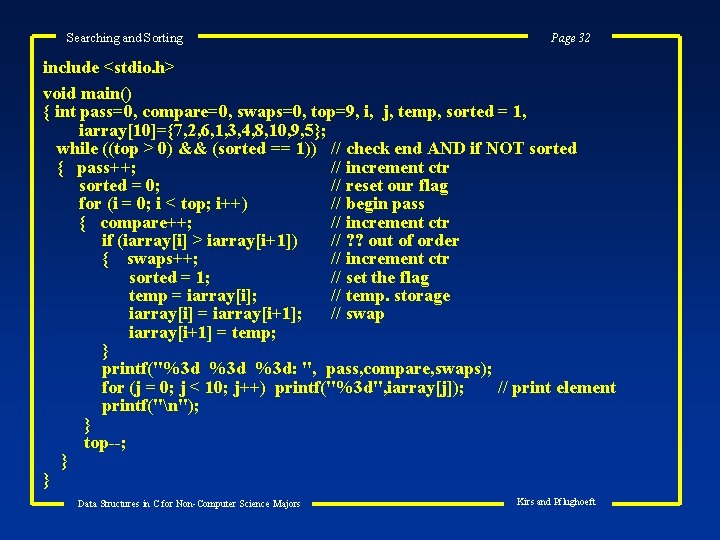
Searching and Sorting Page 32 include <stdio. h> void main() { int pass=0, compare=0, swaps=0, top=9, i, j, temp, sorted = 1, iarray[10]={7, 2, 6, 1, 3, 4, 8, 10, 9, 5}; while ((top > 0) && (sorted == 1)) // check end AND if NOT sorted { pass++; // increment ctr sorted = 0; // reset our flag for (i = 0; i < top; i++) // begin pass { compare++; // increment ctr if (iarray[i] > iarray[i+1]) // ? ? out of order { swaps++; // increment ctr sorted = 1; // set the flag temp = iarray[i]; // temp. storage iarray[i] = iarray[i+1]; // swap iarray[i+1] = temp; } printf("%3 d %3 d: ", pass, compare, swaps); for (j = 0; j < 10; j++) printf("%3 d", iarray[j]); // print element printf("n"); } top--; } } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

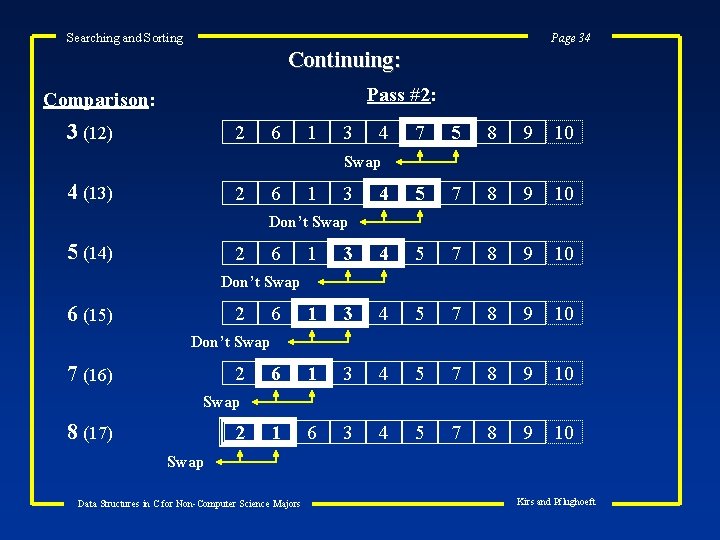
Searching and Sorting Page 33 Could we refine the bubble sort? ? We could ‘bubble - up’ in one pass (as we did before) AND ‘bubble-down’ in the next pass. Consider our list after our first pass (9 th comparison): 2 6 1 3 4 7 8 9 5 10 Starting at the top of the list, we now ‘bubble-down’ the smallest element (‘ 1’ will end up at the bottom of the list): Comparison 1 (10) Pass #2 2 6 1 3 4 7 8 9 5 10 8 5 9 10 Swap 2 (11) 2 6 1 3 4 7 Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 34 Continuing: Pass #2: Comparison: 3 (12) 2 6 1 3 4 7 5 8 9 10 4 5 7 8 9 10 Swap 4 (13) 2 6 1 3 Don’t Swap 5 (14) 2 6 1 3 4 5 7 8 9 10 1 6 3 4 5 7 8 9 10 Don’t Swap 6 (15) 2 6 Don’t Swap 7 (16) 2 Swap 8 (17) 2 Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 35 Continuing: Comparison: 1 (18) Pass #3: 1 2 6 3 4 5 7 8 9 10 9 10 Don’t Swap 2 (19) 1 2 6 3 4 5 Swap 3 (20) 1 2 3 6 4 5 Swap 4 (21) 1 2 3 4 6 5 7 Swap 5 (22) 1 2 3 4 5 6 7 8 Swap 6 (23) 1 2 3 4 5 6 7 8 9 10 Don’t Swap 7 (24) 1 2 3 4 5 6 7 8 9 10 Don’t Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 36 Since the List is in order, Can we Stop? ? NO: Remember, we need one pass WITHOUT a swap Comparison: 1 (25) Pass #4: 1 2 6 3 4 5 7 8 9 10 3 4 5 7 8 9 10 6 3 4 5 7 8 9 10 Don’t Swap 2 (26) 1 2 6 3 4 Don’t Swap 3 (27) 1 2 6 3 Don’t Swap 4 (28) 1 2 6 Don’t Swap 5 (29) 1 2 Don’t Swap 6 (30) 1 2 Don’t Swap Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

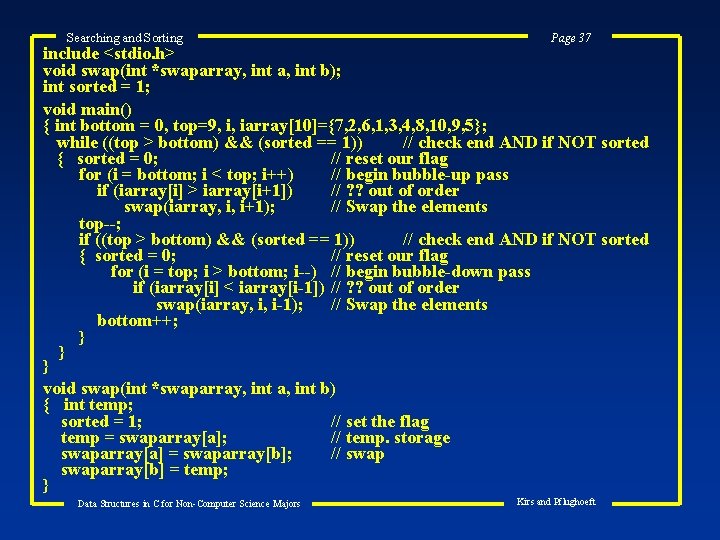
Searching and Sorting Page 37 include <stdio. h> void swap(int *swaparray, int a, int b); int sorted = 1; void main() { int bottom = 0, top=9, i, iarray[10]={7, 2, 6, 1, 3, 4, 8, 10, 9, 5}; while ((top > bottom) && (sorted == 1)) // check end AND if NOT sorted { sorted = 0; // reset our flag for (i = bottom; i < top; i++) // begin bubble-up pass if (iarray[i] > iarray[i+1]) // ? ? out of order swap(iarray, i, i+1); // Swap the elements top--; if ((top > bottom) && (sorted == 1)) // check end AND if NOT sorted { sorted = 0; // reset our flag for (i = top; i > bottom; i--) // begin bubble-down pass if (iarray[i] < iarray[i-1]) // ? ? out of order swap(iarray, i, i-1); // Swap the elements bottom++; } } } void swap(int *swaparray, int a, int b) { int temp; sorted = 1; // set the flag temp = swaparray[a]; // temp. storage swaparray[a] = swaparray[b]; // swaparray[b] = temp; } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 38 Are there better sorting methods? YES: Generally speaking, bubble sorts are very slow The Quicksort Method: • Generally the fastest internal sorting method • intended for longer lists How does a quicksort work? • As we have seen, the shorter the list, the faster the sort • Quicksort recursively partitions the list into smaller sublists, gradually moving the elements into their correct position Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

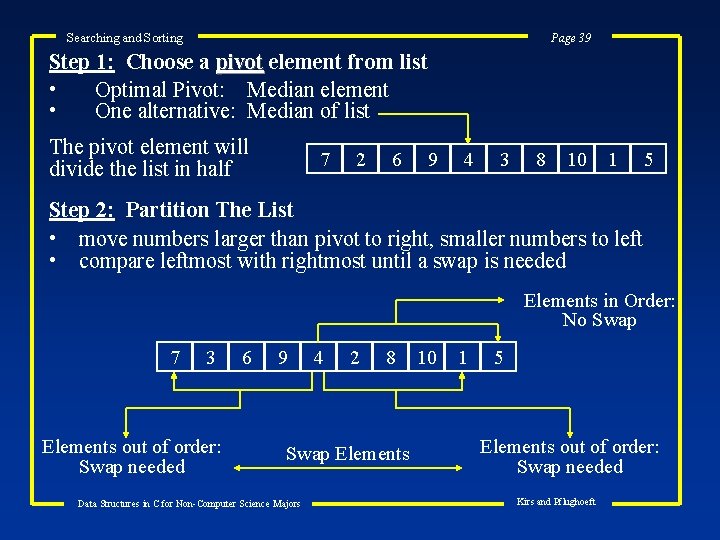
Searching and Sorting Page 39 Step 1: Choose a pivot element from list • Optimal Pivot: Median element • One alternative: Median of list The pivot element will divide the list in half 7 2 6 9 4 3 8 10 1 5 Step 2: Partition The List • move numbers larger than pivot to right, smaller numbers to left • compare leftmost with rightmost until a swap is needed Elements in Order: No Swap 7 3 Elements out of order: Swap needed 6 9 4 2 8 Swap Elements Data Structures in C for Non-Computer Science Majors 10 1 5 Elements out of order: Swap needed Kirs and Pflughoeft

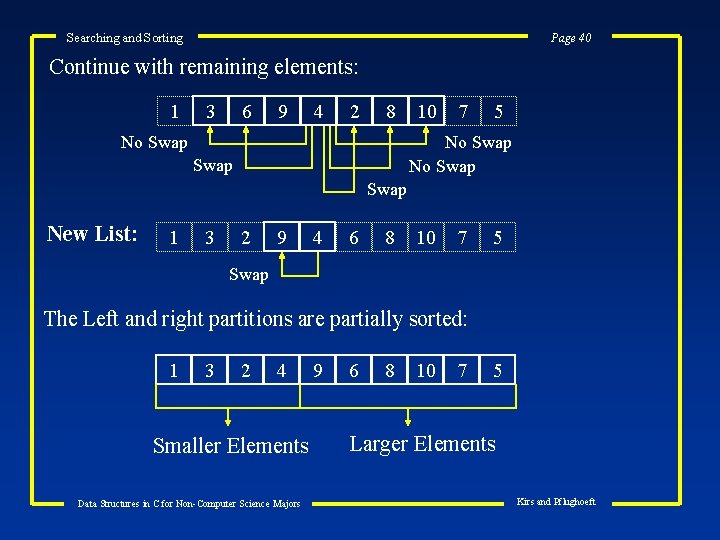
Searching and Sorting Page 40 Continue with remaining elements: 1 3 6 9 4 2 8 No Swap 10 7 5 No Swap New List: 1 3 2 9 4 6 8 10 7 5 Swap The Left and right partitions are partially sorted: 1 3 2 4 Smaller Elements Data Structures in C for Non-Computer Science Majors 9 6 8 10 7 5 Larger Elements Kirs and Pflughoeft

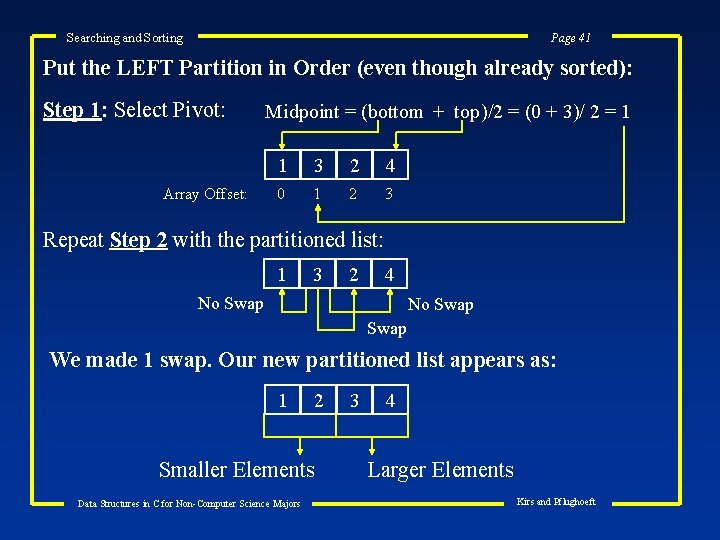
Searching and Sorting Page 41 Put the LEFT Partition in Order (even though already sorted): Step 1: Select Pivot: Array Offset: Midpoint = (bottom + top)/2 = (0 + 3)/ 2 = 1 1 3 2 4 0 1 2 3 Repeat Step 2 with the partitioned list: 1 3 2 4 No Swap We made 1 swap. Our new partitioned list appears as: 1 2 Smaller Elements Data Structures in C for Non-Computer Science Majors 3 4 Larger Elements Kirs and Pflughoeft

Searching and Sorting Page 42 OK – So the list is in order. We can stop, Right? ? ? Not really. The only way to be sure that the complete list is in order is to keep breaking the list down until there no swaps are made or there is only one element on each sublist. 1 2 Looking at the left sublist: All we know is that the elements on it are smaller 2 1 than the elements on the right sub-list. The order could have been: Assume that it was the sublist above. We have to continue making sublists: The list midpoint is (0 + 1)/2 = 0 2 1 Swap NOW we are done since each sublist contains only one element Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

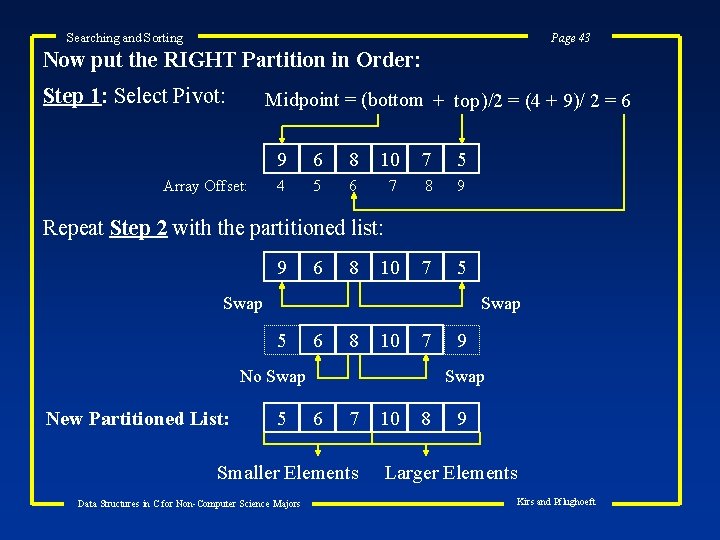
Searching and Sorting Page 43 Now put the RIGHT Partition in Order: Step 1: Select Pivot: Midpoint = (bottom + top)/2 = (4 + 9)/ 2 = 6 Array Offset: 9 6 8 10 7 5 4 5 6 7 8 9 10 7 5 Repeat Step 2 with the partitioned list: 9 6 8 Swap 5 6 8 10 7 No Swap New Partitioned List: 5 Swap 6 7 Smaller Elements Data Structures in C for Non-Computer Science Majors 9 10 8 9 Larger Elements Kirs and Pflughoeft

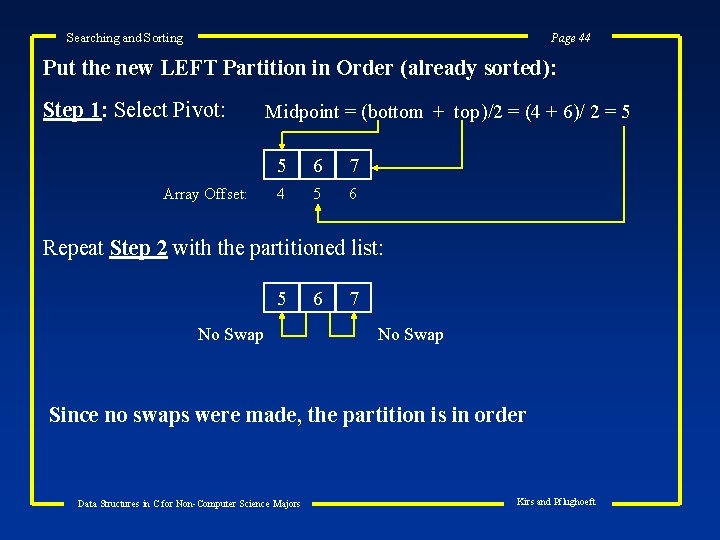
Searching and Sorting Page 44 Put the new LEFT Partition in Order (already sorted): Step 1: Select Pivot: Array Offset: Midpoint = (bottom + top)/2 = (4 + 6)/ 2 = 5 5 6 7 4 5 6 Repeat Step 2 with the partitioned list: 5 No Swap 6 7 No Swap Since no swaps were made, the partition is in order Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

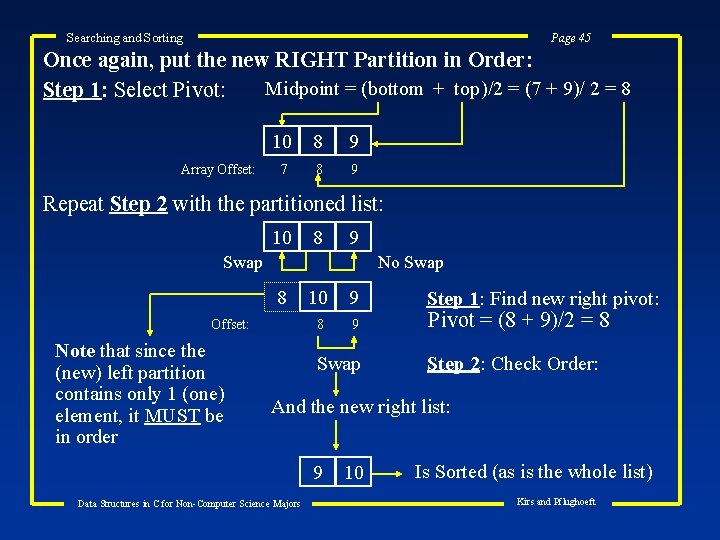
Searching and Sorting Page 45 Once again, put the new RIGHT Partition in Order: Midpoint = (bottom + top)/2 = (7 + 9)/ 2 = 8 Step 1: Select Pivot: Array Offset: 10 8 9 7 8 9 Repeat Step 2 with the partitioned list: 10 8 9 Swap No Swap 8 Offset: Note that since the (new) left partition contains only 1 (one) element, it MUST be in order 10 9 8 9 Swap Step 1: Find new right pivot: Pivot = (8 + 9)/2 = 8 Step 2: Check Order: And the new right list: 9 Data Structures in C for Non-Computer Science Majors 10 Is Sorted (as is the whole list) Kirs and Pflughoeft

Searching and Sorting Page 46 This seems very complicated. Is it worth it? ? Maybe: • For our list, we needed 22 comparisons and 7 swaps (vs. 30 comparisons and 15 swaps for our 2 -ways sort with checks). • The WORST case scenario for a quicksort is: log 2 n! Comparing a quicksort with a Bubble Sort: Sort Elements Max. Bubble Sort 10 100 1, 000 10, 000 45 4, 950 999, 500 49, 995, 000 Max Quicksort 22 525 9, 965 132, 877 What About the C Code necessary ? ? It’s pretty simple, but it involves a new procedure: RECURSION Recusion is when a function calls itself. Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 47 #include <stdio. h> int quicksort(int a[], int first, int last); void swap(int *a, int *b); void main() { int iarray[10] = {7, 2, 6, 9, 4, 3, 8, 10, 1, 5}; quicksort(iarray, 0, 9); } int quicksort(int list[], int first, int last) { int lower = first, upper = last, bound = list[(first + last)/2]; while (lower <= upper) { while (list[lower] < bound) lower++; while (bound < list[upper]) upper--; } if (lower < upper) swap(&list[lower++], &list[upper--]); } else lower++; if (first < upper) quicksort(list, first, upper); if (upper + 1 < last) quicksort(list, upper+1, last); } void swap(int *a, int *b) { int i, temp; temp = *a; *a = *b; *b = temp; } Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Page 48 Why is sorting important? ? This illustrates a major trade-off in programming: • Finding elements in a list is much quicker if the list is sorted (as we have seen, a binary search is exponentially faster than a sequential search) • Sorting is a difficult and time-consuming task (as is maintaining a sorted list) Data Structures in C for Non-Computer Science Majors Kirs and Pflughoeft

Searching and Sorting Data Structures in C for Non-Computer Science Majors Page 49 Kirs and Pflughoeft