Geometry Page 2 Page 3 Page 6 Page

Geometry Page 2 Page 3 Page 6 Page 9 Page 11 Page 17 Page 21 Page 24 Index Basic rules Transformation Geometry 1 – example questions Congruent triangles question Parallelograms – example questions Circumcircle and Incircle More Transformations Chapter 1 Revision Exercises

Basic Rules Two Main Rules: Triangle Rule Straight line rule Isosceles Triangle Congruent Triangles 15: 57 Parallel Lines Vertically Opposite Corresponding Alternate Parallelogram Opposite angles and sides of a parallelogram are equal

Transformation Geometry Made up of three topics: Axial Symmetry Central Symmetry Transformation Materials Required: Ruler Set Square

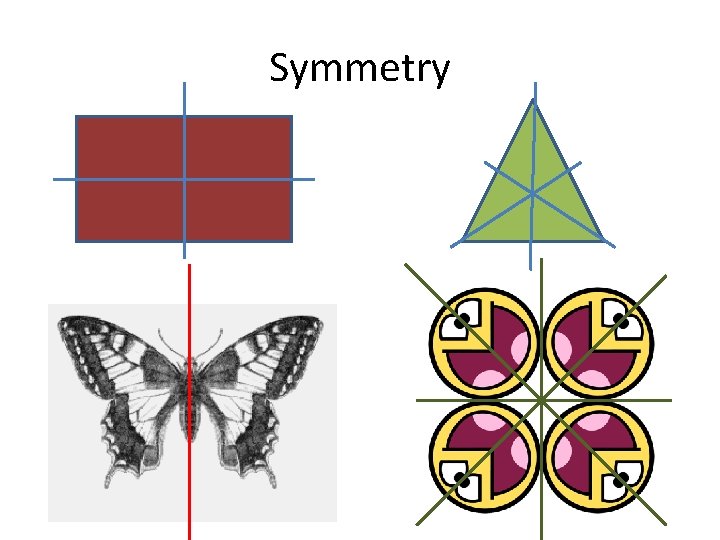
Symmetry

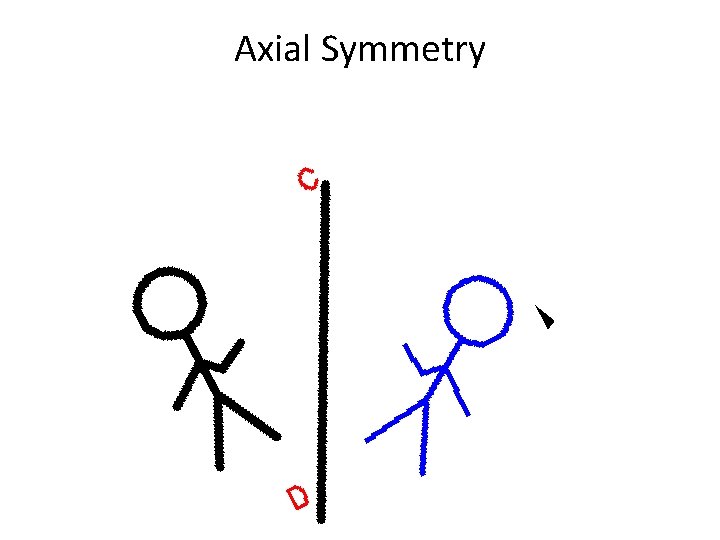
Axial Symmetry

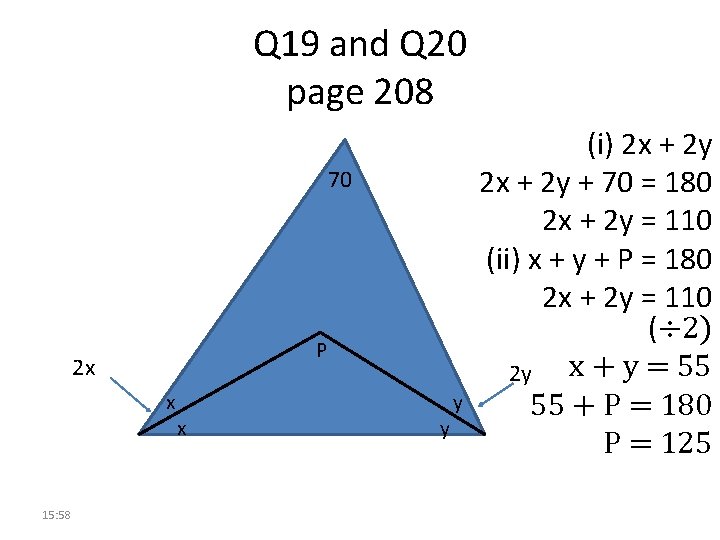
Q 19 and Q 20 page 208 70 P 2 x x 15: 58 x y y (i) 2 x + 2 y + 70 = 180 2 x + 2 y = 110 (ii) x + y + P = 180 2 x + 2 y = 110 (÷ 2) x + y = 55 2 y 55 + P = 180 P = 125

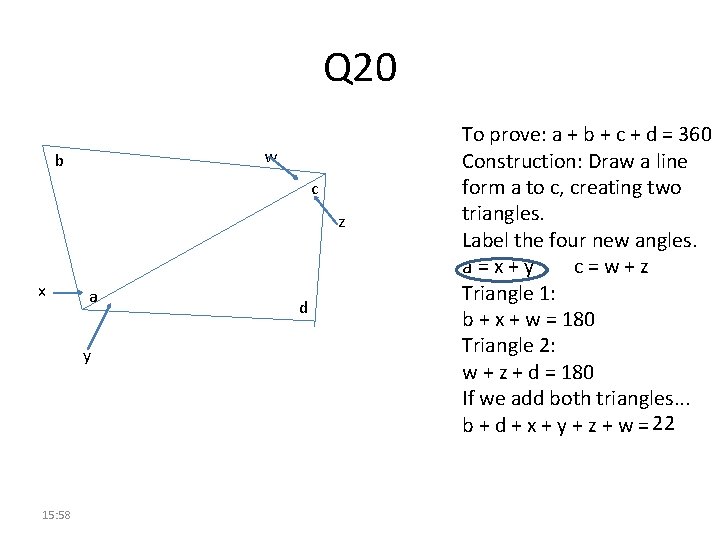
Q 20 w b c z x a y 15: 58 d To prove: a + b + c + d = 360 Construction: Draw a line form a to c, creating two triangles. Label the four new angles. a=x+y c=w+z Triangle 1: b + x + w = 180 Triangle 2: w + z + d = 180 If we add both triangles. . . b + d + x + y + z + w = 22

Q 8 page 217 Before we attempt this. . Prove △dcx ≡ △bxd S bd = dc (d bisects the line) S xd = xd (common Line) A <bdx = <xdc (both 90°) This shows they are congruent through SAS. We can also say that bx = xc as any point on the perpendicular bisector of two points, is equal distance from those two points. . (don’t be confused!) 15: 58 Prove that <abx and <axc have equal area. . If they are congruent they have equal area! ac = ab (lines on a perp. bisector) bc = xc (same reason) ax = ax (common line) <abx ≡ <axc (SSS) Both have same area!

Exercise on congruent triangles Prove that △abc ≡ △ecd <abc = <def <acb = <dfe Given bc = ce (C is midpoint) Angles on parallel lines <bca =<ecd (opposite angle) We need a side to show they are congruent (common line) <abc =<ced (Alternate angles) dc = dc ad = cf (given) △abc ≡ △ecd ASA So. . . ad + dc =dc + cf Therefore ac = df △abc ≡ △def (ASA) 15: 58

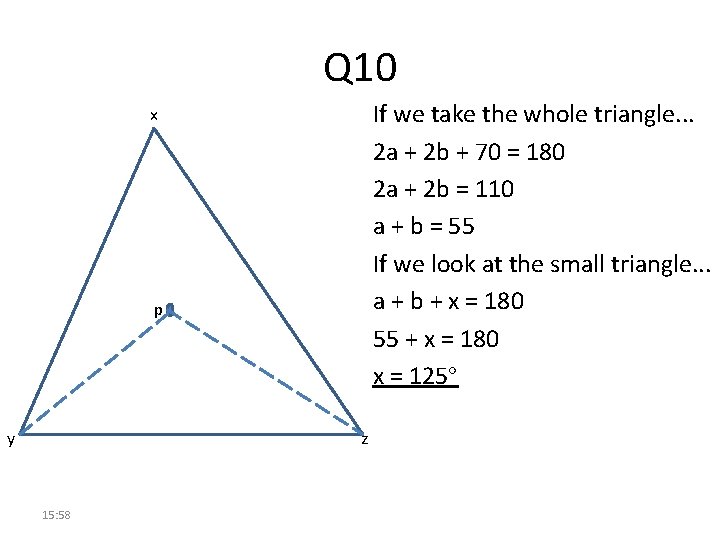
Q 10 If we take the whole triangle. . . 2 a + 2 b + 70 = 180 2 a + 2 b = 110 a + b = 55 If we look at the small triangle. . . a + b + x = 180 55 + x = 180 x = 125° x p y z 15: 58

Parallelogram

Parallelogram Theorem To Prove: Opposite angles and opposite sides of a parallelogram are equal in measure. a Given: The parallelogram abcd To Prove: l ab l = l cd l and l ac l = l bd l Also l<abd l = l <acd l and l <cab l = l <cdb l Construction: Draw the line l cb l and Label the new angles Q, R, S and T (Note: If we can show the two new triangles are Q S congruent, it will help prove theorem) c (Parallel Lines? ) Q = T and S = T (Alternate angles) l cb l = l cb l (common line) Therefore △acb and △acb are congruent (ASA) Therefore l ab l = l cd l and l ac l = l bd l Also. . . Q = T and S = R (alternate angles) So. . . Q+S=T+R 15: 58 l<abd l = l <acd l and l <cab l = l <cdb l Therefore b R T d

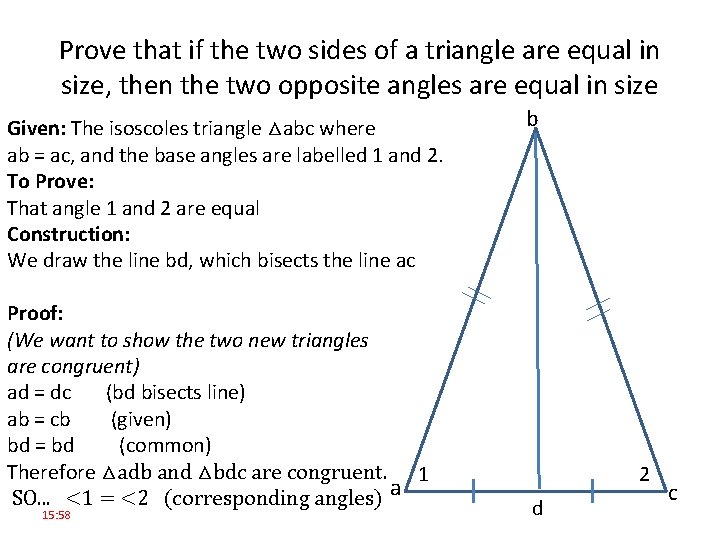
Prove that if the two sides of a triangle are equal in size, then the two opposite angles are equal in size Given: The isoscoles triangle △abc where ab = ac, and the base angles are labelled 1 and 2. To Prove: That angle 1 and 2 are equal Construction: We draw the line bd, which bisects the line ac Proof: (We want to show the two new triangles are congruent) ad = dc (bd bisects line) ab = cb (given) bd = bd (common) Therefore △adb and △bdc are congruent. 1 SO. . . <1 = <2 (corresponding angles) a 15: 58 b 2 d c

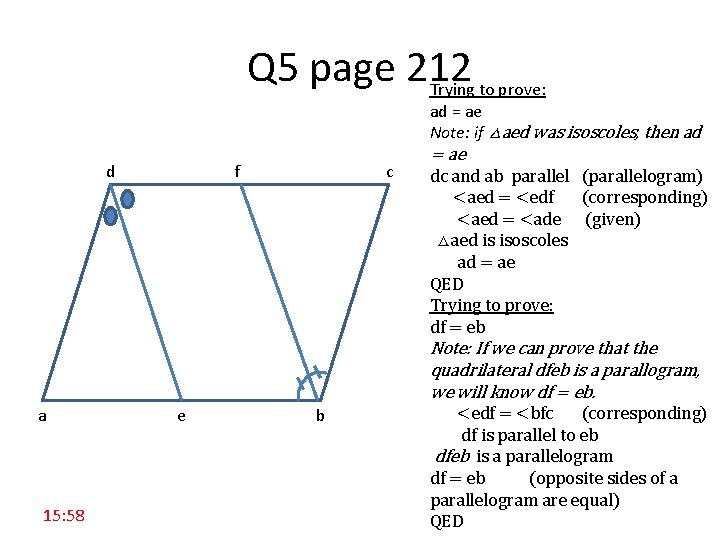
Q 5 page 212 Trying to prove: ad = ae Note: if △aed was isoscoles, then ad d f c = ae dc and ab parallel (parallelogram) <aed = <edf (corresponding) <aed = <ade (given) △aed is isoscoles ad = ae QED Trying to prove: df = eb Note: If we can prove that the quadrilateral dfeb is a parallogram, we will know df = eb. a 15: 58 e b <edf = <bfc (corresponding) df is parallel to eb dfeb is a parallelogram df = eb (opposite sides of a parallelogram are equal) QED

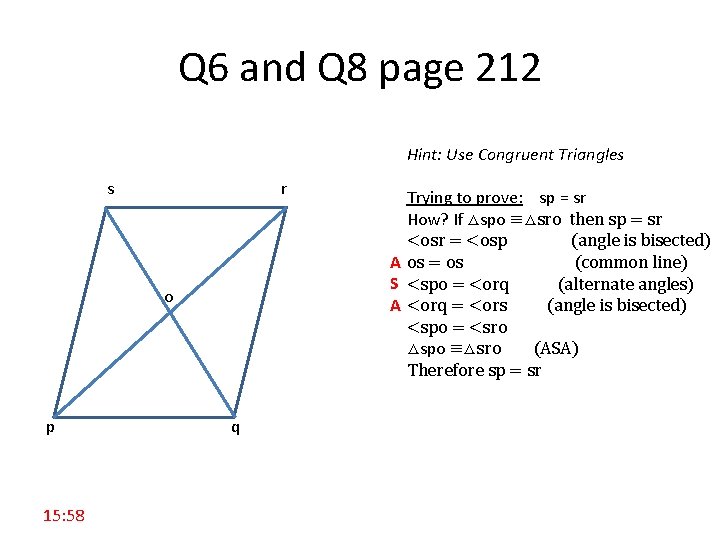
Q 6 and Q 8 page 212 Hint: Use Congruent Triangles s r o p 15: 58 q Trying to prove: sp = sr How? If △spo ≡△sro then sp = sr <osr = <osp (angle is bisected) A os = os (common line) S <spo = <orq (alternate angles) A <orq = <ors (angle is bisected) <spo = <sro △spo ≡△sro (ASA) Therefore sp = sr

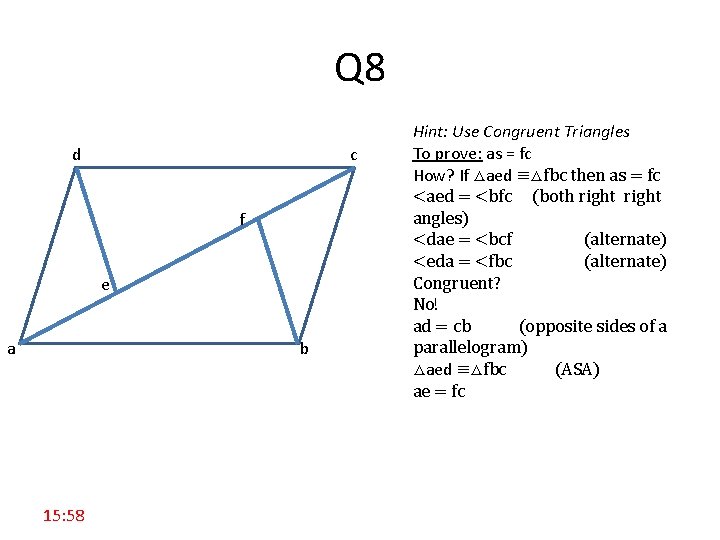
Q 8 d c f e a b 15: 58 Hint: Use Congruent Triangles To prove: as = fc How? If △aed ≡△fbc then as = fc <aed = <bfc (both right angles) <dae = <bcf (alternate) <eda = <fbc (alternate) Congruent? No! ad = cb (opposite sides of a parallelogram) △aed ≡△fbc (ASA) ae = fc

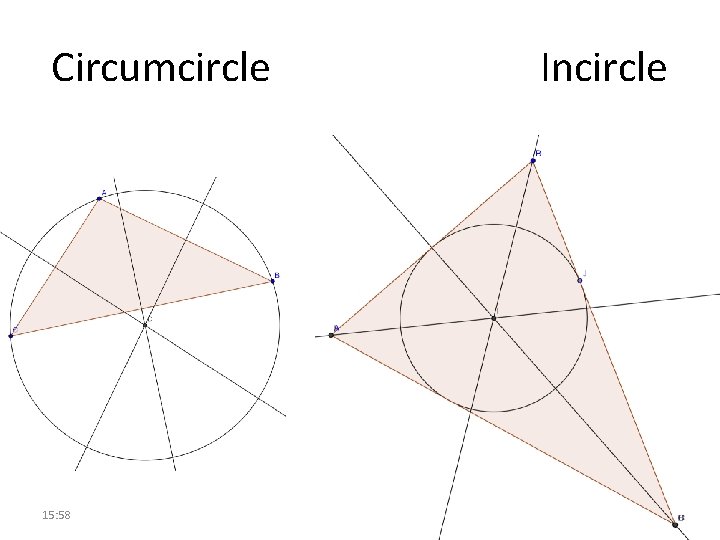
Circumcircle 15: 58 Incircle

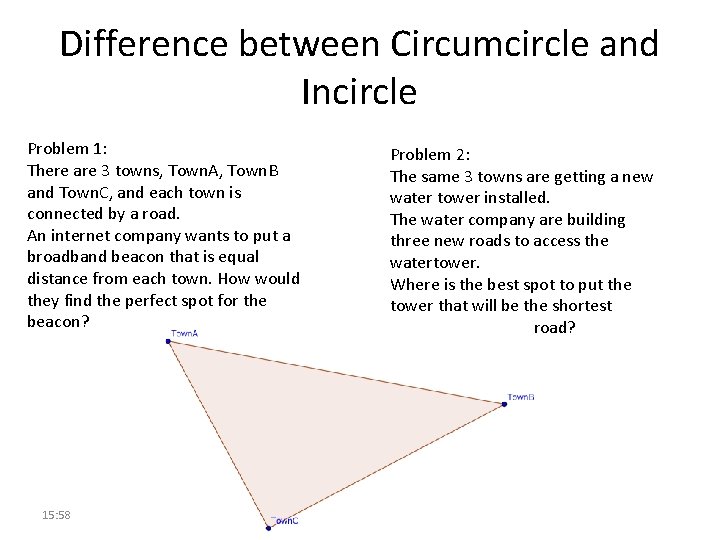
Difference between Circumcircle and Incircle Problem 1: There are 3 towns, Town. A, Town. B and Town. C, and each town is connected by a road. An internet company wants to put a broadband beacon that is equal distance from each town. How would they find the perfect spot for the beacon? 15: 58 Problem 2: The same 3 towns are getting a new water tower installed. The water company are building three new roads to access the watertower. Where is the best spot to put the tower that will be the shortest distance from each road?

Homework Area of △boc: A = ½bh A = ½(6)(3) A = ½(18) A = 9 cm² Area of △abc: What if we create 2 more triangles similar to △boc 15: 58 Area of △boa: A = ½bh A = ½(5)(3) A = 7. 5 cm² Area of △aoc A = ½bh A = ½(4)(3) A = 6 cm² Total area: 9 + 7. 5 + 6 Area = 22. 5 cm²

Ctd. . . If we are told the point is the circumcircle of a triangle what do we know. . ? We know that the distances between the point and the three corners are equal. If we are told the point is the incircle of a triangle what do we know. . ? We know that the Perpendicular distances between the point and the three sides are equal 15: 58

Transformations 15: 58

HW Q 6 E A F G (i) A onto B (ii) C onto E (iii) A onto C (iv) F onto G D H C 15: 58 B (v) B onto E (vi) D onto F

Homework Q 8 Page 225 (i) Onto A: Central Symmetry (or rotation) (ii) Onto B Translation (iii) Onto C Central Symmetry (iv) Onto D Axial symmetry (v) Onto E Axial Symmetry 15: 58

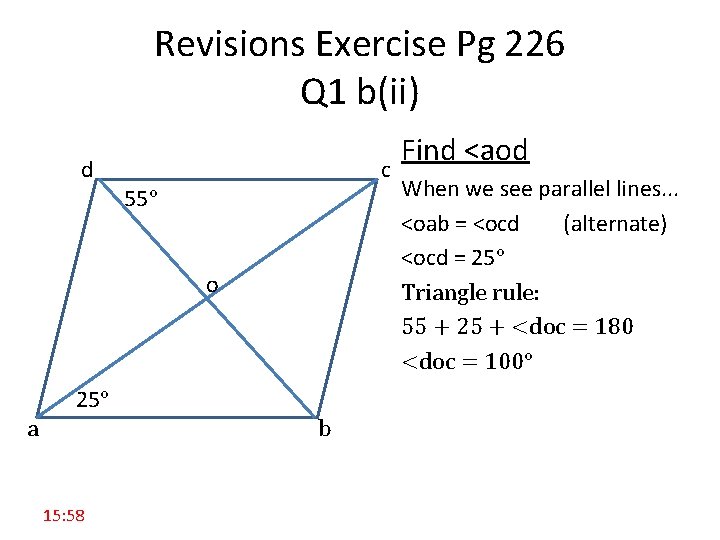
Revisions Exercise Pg 226 Q 1 b(ii) d c 55° o 25° a b 15: 58 Find <aod When we see parallel lines. . . <oab = <ocd (alternate) <ocd = 25° Triangle rule: 55 + 25 + <doc = 180 <doc = 100°

Part C (i) Prove that [da] = [dc] Try and prove by congruency. . . [ba] = [bc] (given) <cbd = <abd (angle bisected) [bd] = [bd] (common line] △abd ≡ △bcd SAS (ii) Prove that ad ⊥ dc [bd] is a bisector of [ac] B is a point on the bisector [bc] = [ba] (given at start) [bd] must be the perpendicular bisector! 15: 58

Q 2. b(ii) 5² + [oa]² = 13² [oa]² = 169 – 25 [oa]²= 144 15: 58 [oa]= 12 Find [oa] If we can prove [ap] = [bp] then we can use pythagoras. Congruency: △pbo ≡ △poa SAS or [op] bisects <aop Any point, on the bisector of the angle between two lines, has the same perpendicular distance from the two lines. Therefore [pb] = [ap]

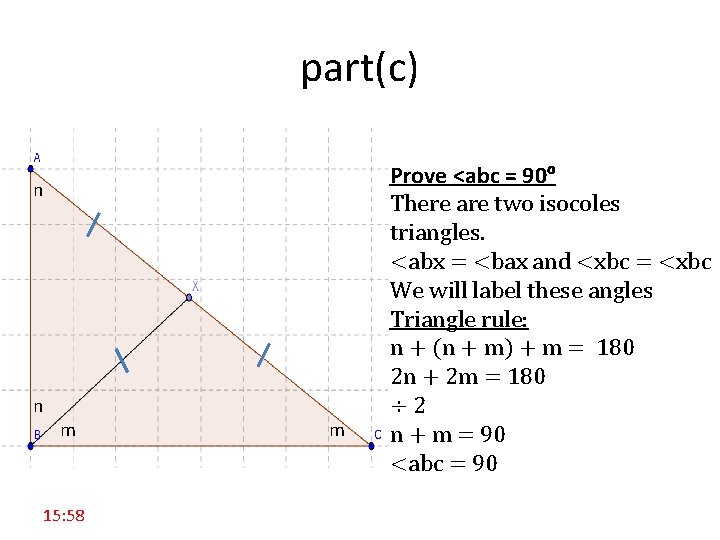
part(c) n n m 15: 58 m Prove <abc = 90° There are two isocoles triangles. <abx = <bax and <xbc = <xbc We will label these angles Triangle rule: n + (n + m) + m = 180 2 n + 2 m = 180 ÷ 2 n + m = 90 <abc = 90

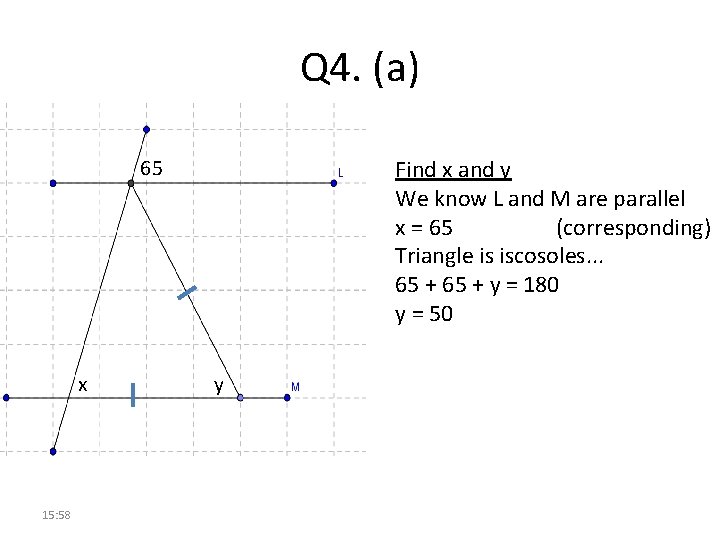
Q 4. (a) Find x and y We know L and M are parallel x = 65 (corresponding) Triangle is iscosoles. . . 65 + y = 180 y = 50 65 x 15: 58 y

Find <acb in terms of x We know △dca is iscosoles. . . So <cad = x We can now get <acd in terms of x x + <acd = 180 – 2 x Q 4 (c) x x If [ad] = [bd] what does that mean? △adb is an iscosoles. . . <dba = <dab 2 x = 180 – 3 x 5 x = 180 x = 15: 58 36° <acb + <acd = 180 <acb + 180 – 2 x = 180 <acb = 2 x Find <bad in terms of x If <acb = 2 x then <dba = 2 x 2 x + <bac = 180 – 4 x <bad = 180 – 4 x + x

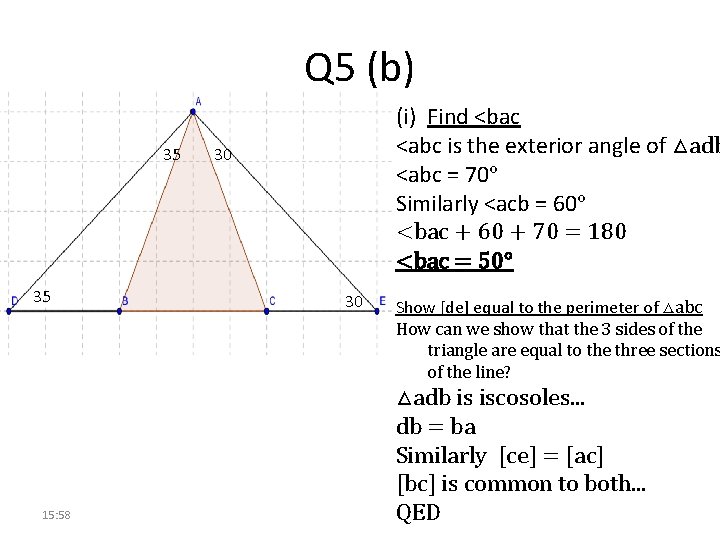
Q 5 (b) 35 35 15: 58 (i) Find <bac <abc is the exterior angle of △adb <abc = 70° Similarly <acb = 60° <bac + 60 + 70 = 180 <bac = 50° 30 30 Show [de] equal to the perimeter of △abc How can we show that the 3 sides of the triangle are equal to the three sections of the line? △adb is iscosoles. . . db = ba Similarly [ce] = [ac] [bc] is common to both. . . QED

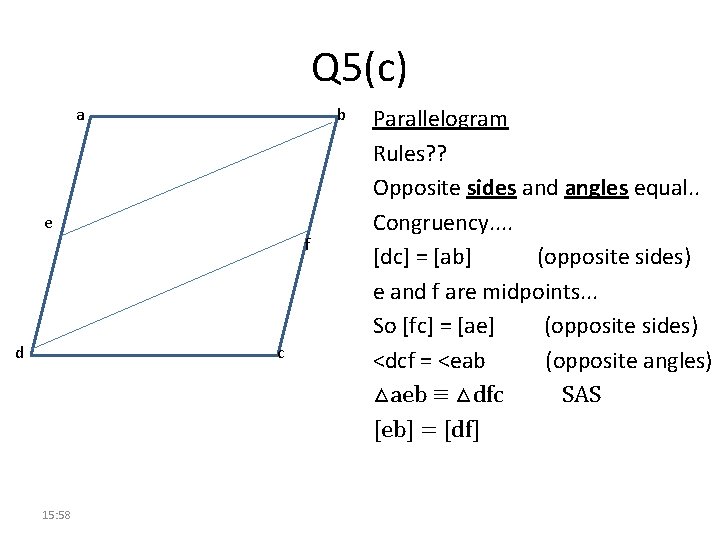
Q 5(c) a b e d f c 15: 58 Parallelogram Rules? ? Opposite sides and angles equal. . Congruency. . [dc] = [ab] (opposite sides) e and f are midpoints. . . So [fc] = [ae] (opposite sides) <dcf = <eab (opposite angles) △aeb ≡ △dfc SAS [eb] = [df]