SD Natural Deduction in S Gregory Chapter 4

SD: Natural Deduction in S Gregory Chapter 4

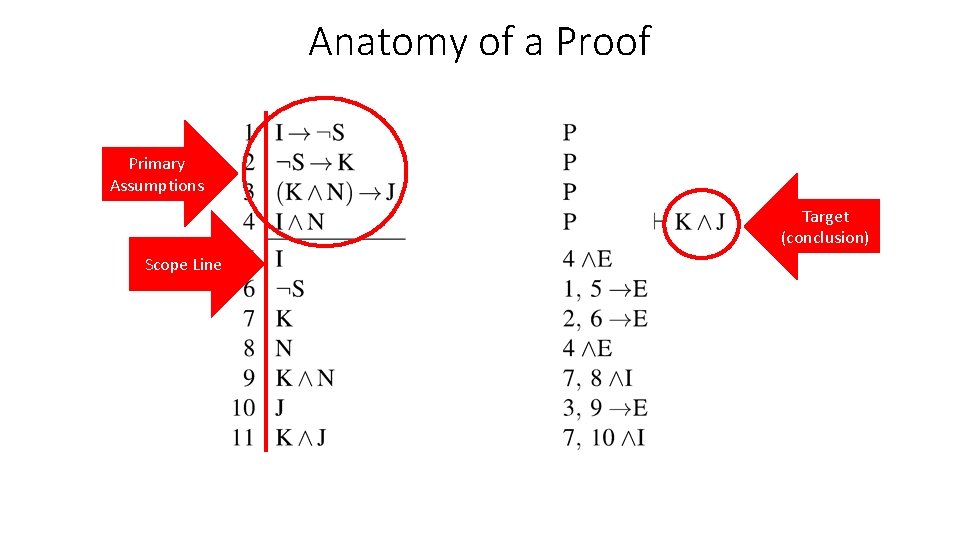
Anatomy of a Proof Primary Assumptions Target (conclusion) Scope Line

What is Natural Deduction? • A (very) brief history of logic (cultural enrichment) - Aristotelian Logic and its elaborations - Boole, Peirce, Frege, Principia and beyond: Axiomatic Systems & Natural Deduction • The Rules of Inference - Each of the 5 connectives has an introduction rule and an elimination rule. - The Reiteration Rule allows lines of the proof to be repeated. • The Rules are truth-preserving! • Two concepts of validity: semantic entailment (⊨ ) and derivability (⊢)

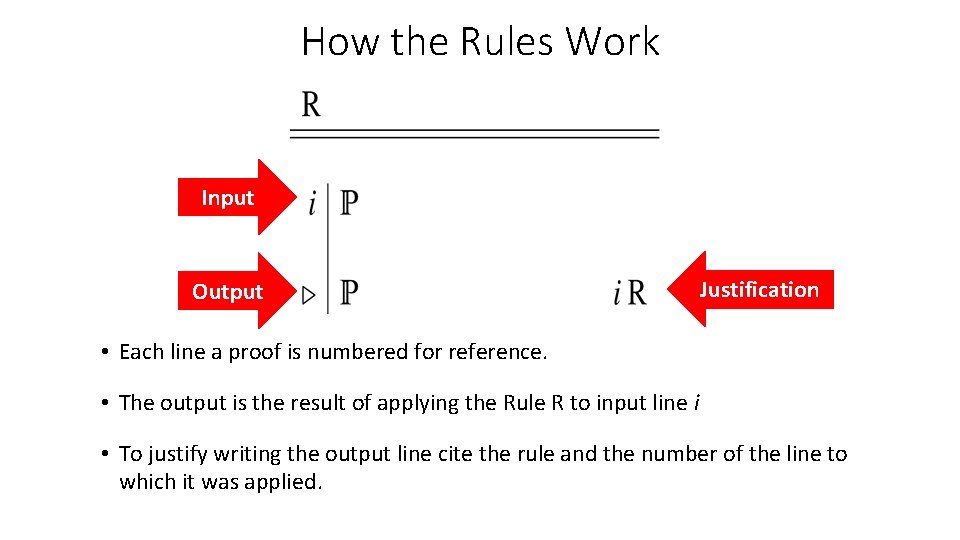
How the Rules Work Input Output Justification • Each line a proof is numbered for reference. • The output is the result of applying the Rule R to input line i • To justify writing the output line cite the rule and the number of the line to which it was applied.

4. 1 Connective in and out rules

Wedge Rules - ∧I and ∧E • Note: like all the Rules of Inference they can only be applied to whole lines. • Note: Like all the Rules they can be shown to be truth preserving via truth tables.

∧I: Example • Each of the moves is legal--this shows you what can be done with the rule • But lines 4 and 5 are irrelevant to the proof.

∧E: Example • Note: cant derive 4 directly from 1! • Correct application of a rule matter of syntax and symbolic form!

Arrow Rules - →I and →E • →E mimics modus ponens • →I involves a subderivation, beginning with the auxiliary assumption ℙ marked off by a new scope line and horizontal - The idea is we’re saying ‘what if ℙ … from which we derive ℚ … - So we conclude that if we had ℙ the we’d get ℚ, i. e. ℙ → ℚ

→E: Example • How do we know where to start? We think our way back from the goal until we can start. • We look for the conclusion in the premises • And by successive application of rules get it out

→I: Example • We want to prove a conditional, I → (¬ G ∧ R). • We assume the antecedent, I, writing ‘A’ as justification for the line, indenting and introducing new scope line--to enter the World of What If. • We derive the consequent. • Pop out of the World of What-If, ‘discharging’ the assumption, citing line numbers of subderivation.

Negation Rules - ¬I and ¬E • Reductio ad Absudum rules: compare to truth tree test for validity! • We assume the opposite of what we want to prove and show that it implies a contradiction: a sentence and the negation of that sentence. • Which shows the assumption was bad--and so we can infer the opposite of the assumption.

¬E: Example • We want to prove S • Going into the World of What-If we assume ¬ S • And show that ¬ S is bad since it leads to both ¬ J and J • Since ¬ S is bad, S is good! • So we discharge the sequence, writing S

Vee Rules - ∨I and ∨E • ∨I: You are not getting something for nothing here (I’ll explain) • ∨E: Constructive Dilemma: Either ℙ or ℚ , if ℙ we get ℝ and if ℚ we get ℝ. Gotta be one or the other and either way, we get ℝ

∨I: Example • We need to make the antecedent of 2 to get ¬ K • So add N to S by ∨I • Note: this only works with ∨! The result of applying the rule is not stronger than the sentence to which it was applied!

∨E: Example • We want F • We have either S or N and • The S road and N road both lead to F • So we have F

Double Arrow Rules - ↔I and ↔E • Biconditional is conditional going both ways--equivalent to conjunction of the two conditionals so… • ↔I is like →I twice over and… • ↔E is like →E -- and can be done on either of the conditionals.

↔ I and E: Example

4. 1. 7 Exercises

4. 2 Derivations: Strategies & Notes Strategy game--there is no algorithm for doing proofs

Goal Analysis - Working Backward

Subderivations

Subderivations Example

Proving a Tautology • Remember, a tautology can be derived from the empty set of sentences - Since there’s no TVA on which a tautology is false, in any argument where the conclusion is a tautology, there’s no TVA in which the premises, whatever they are, if any, are true and the conclusion is false. • Proving a tautology is deriving it from the empty set of sentences.

4. 3 Proof Theory in SD

Derivations in SD

Other Properties Theorem of SD: A WFF ℙ is a theorem of SD iff ℙ is derivable from the empty set, i. e. , iff ⊢ ℙ. Equivalent in SD: Two WFFs ℙ and ℚ are equivalent in SD iff they are interderivable in SD, i. e. , iff both ℙ ⊢ ℚ and ℚ ⊢ ℙ. Inconsistent in SD: A set Γ of WFFs is inconsistent in SD iff, for some WFF ℙ, both Γ ⊢ ℙ and Γ ⊢ ¬ ℙ.

4. 3. 1 Exercises

4. 4 SDE, an Extention to SD More rules to make life easier which can be proven from what we already have

4. 4. 1 Additional Inference Rules of SDE

Proving the New Rules

Examples

4. 4. 2 Exercises

4. 4. 3 The Replacement Rules of SD • Replacement rules are bidirectonal--inference rules are not. • Replacement rules apply to both WFFs and well-formed components of WFFs-inference rules apply only to WFFs (whole lines)!

4. 4. 3 The Replacement Rules of SDE

4. 4. 4 Exercises

The Happy Marriage of Semantics & Syntax