Natural Deduction Formal Methods in Verification of Computer

Natural Deduction Formal Methods in Verification of Computer Systems Jeremy Johnson

Outline 1. An example 1. Validity by truth table 2. Validity by proof 2. What’s a proof 1. Proof checker 3. Rules of natural deduction 4. Provable equivalence 5. Soundness and Completeness

An Example • If the train arrives late and there are no taxis at the station, then John is late for his meeting. John is not late for his meeting. The train did arrive late. Therefore, there were taxis at the station. • If it is raining and Jane does not have here umbrella with her, then she will get wet. Jane is not wet. It is raining. Therefore, Jane has her umbrella with her.

An Example

An Example

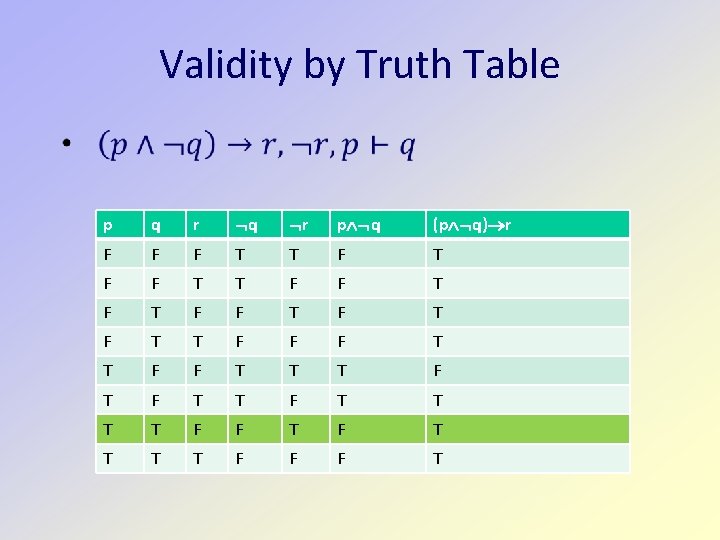
Validity by Truth Table p q r q r p q (p q) r F F F T T F F T F T F T T F F T T T F T T T T F F F T

Proof

Proof • A proof is a sequence of formulas that are either premises or follow from the application of a rule to previous formulas • Each formula must be labeled by it’s justification, i. e. the rule that was applied along with pointers to the formulas that the rule was applied to • It is relatively straightforward to check to see if a proof is valid

Validity by Deduction 1 premise 2 premise 3 premise 4 assumption 5 6 r 7 8 9 q

Rules of Natural Deduction • Natural deduction uses a set of rules formally introduced by Gentzen in 1934 • The rules follow a “natural” way of reasoning about • Introduction rules • Introduce logical operators from premises • Elimination rules • Eliminate logical operators from premise producing a conclusion without the operator

Conjunction Rules • Introduction Rule i • Elimination Rule e 1 e 2

Implication Rules • Introduction Rule … Assume and show i • Elimination Rule (Modus Ponens) e

Disjunction Rules • Introduction Rule i 1 i 2 • Elimination Rule (proof by case analysis) … … e

Negation Rules

Negation Rules • Introduction Rule leads to a contradiction • Double negation e

Proof by Contradiction • Derived Rule Assume and derive a a contradiction • Derived rules can be used like the basic rules and serve as a short cut (macro) • Sometimes used as a negation elimination rule instead of double negation

Law of the Excluded Middle 1 (p p) 2 3 assumption Assumption (p p) 4 5 p 6 p p 7 8 (p p) 9 p p

Proof. Lab • The Proof. Lab tool from the Logic and Proofs course from the CMU online learning initiative allows you to experiment with natural deduction proofs

Proof. Lab

Provable Equivalence

De Morgan’s Law (P Q) P Q 1 (P Q) 2 3 premise assumption P Q i 1 2 e 1, 3 4 5 P 6 Q 7 P Q i 2 6 e 1, 7 8 9 10 P Q i 5, 9

De Morgan’s Law (P Q) P Q 1 P Q premise 2 e 1 1 3 e 2 1 4 assumption 5 P e 2, 5 6 7 assumption Q i 2 6 8 e 3, 7 9 e 4, 5 -6, 7 -8 10 (P Q) i 4 -9

Semantic Entailment

Soundness and Completeness

Proof Outline • For soundness show, using a truth table, that each rule of inference implies the conclusion is true when the assumptions are true and use induction on the length of the proof to chain together inferences • For completeness 1. Reduce to proving tautologies 2. Provide a proof for a sequent for each entry in the truth table for the conclusion using induction on the formula in the conclusion 3. Construct proof from the proofs for each row

Illustrate Inductive Proof 1 p q r 2 premise assumption 3 q assumption 4 p q 5 r e 1, 5 6 q r i 3 -5 7 p (q r) i 2 -6

Smaller Proof Remove last line 1 p q r 2 premise assumption 3 q assumption 4 p q 5 r e 1, 5 6 q r i 3 -5

Inductive Hypothesis 1 p q r 2 premise 3 q assumption 4 p q 5 r e 1, 5 6 q r i 3 -5

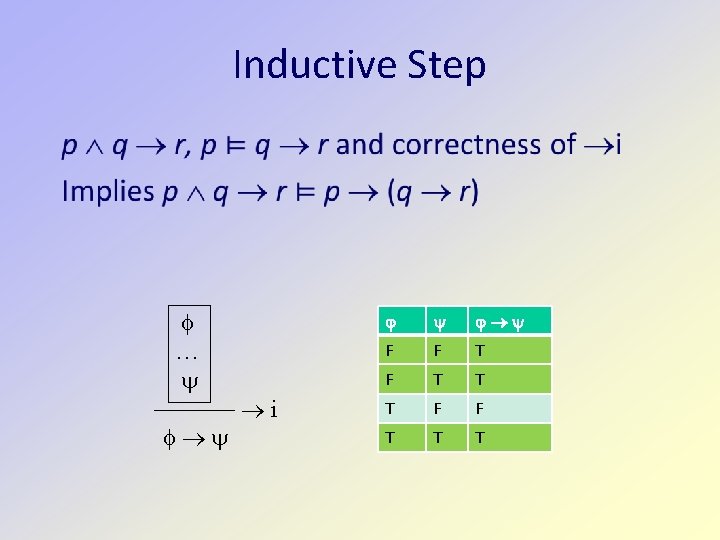
Inductive Step … i F F T T T

Proof of Soundness • Use induction on the length of the proof • Base case. When the proof has length 1, premise and conclusion are the same. Clearly the conclusion is T when the premise is T • Look at the rule in the last line of the proof • Obtain proofs for the premises and use induction hypothesis to show entailment for premises • Use correctness of rule and truth of premises to deduce truth of conclusion

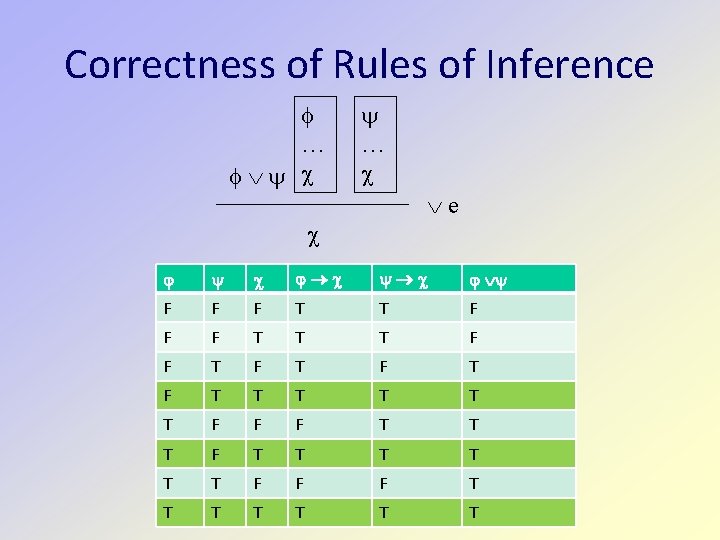
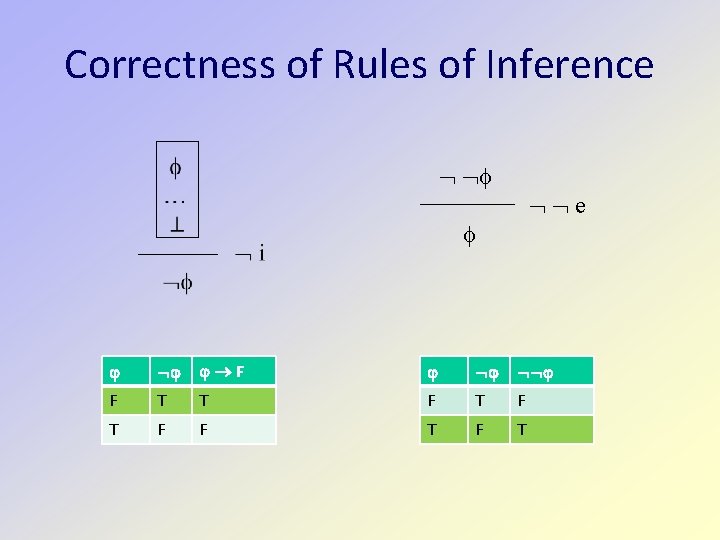
Correctness of Rules of Inference … e F F F T T T F F T F T T T T F F F T T T T

Correctness of Rules of Inference F F T T F T F F T

Induction for Implication Elimination

Inductive Step

Proof of Completeness

Key Lemma for Proof of Completeness

Proof of Lemma

Inductive Step for Implication

Inductive Step for Implication 1 1 2 2 1 3 1 premise assumption 4 5 6 2 1 2 i 3 -5

Inductive Step for Implication 1 1 2 2 1 3 1 premise assumption 4 5 6 2 1 2 i 3 -5

Inductive Step for Implication 1 1 2 2 2 3 1 2 1 1 2 2 1 3 2 4 ( 1 2) 5 2 premise i 3 -5 premise assumption 6 7 ( 1 2) i 4 -6

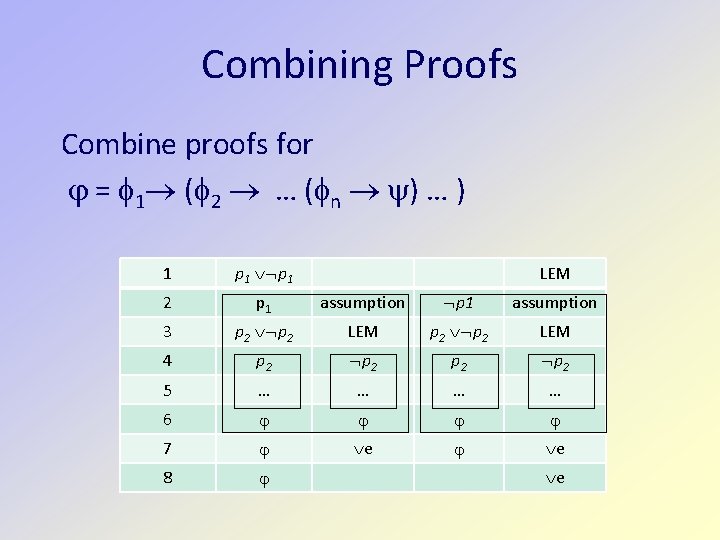
Combining Proofs Combine proofs for = 1 ( 2 … ( n ) … ) 1 p 1 2 p 1 assumption 3 p 2 LEM 4 p 2 5 … … 6 7 e e 8 LEM e