Rfrences Classical electrodynamics John David Jackson Wiley Computational

Références Classical electrodynamics John David Jackson Wiley Computational Electromagnetics Anders Bondeson, Thomas Rylander, Pär Ingelström Springer E-book (accessible sur le campus) : http: //dx. doi. org/10. 1007/b 136922 Ce cours sur le web : http: //bruno. lepetit. pagesperso-orange. fr/teaching. html Une question ? bruno. lepetit@irsamc. ups-tlse. fr 1

modélisation multiphysique à l’échelle méso-macroscopique Plan 1. Introduction : que veut-on calculer ? 2. Rappels d’électromagnétisme 3. Une méthode de résolution des équations de Maxwell : Différences finies domaine temporel 4. Equation de la chaleur : traitement des non-linéarités 5. Applications industrielles Mécanique : Stéphane Guinard, EADS Electromagnétisme : Ivan Revel, EADS 2

Les matériaux : métalliques et composites… 787 Dreamliner Composite Profile

Les composites : fibres et résines Délaminages

Composite ; un empilement complexe : plis, protection de surface, peinture

Un matériau doit assurer une multitude de fonctions : tenue mécanique (efforts, chocs), thermique, protection électromagnétique (champs forts, foudre effets directs et indirects, électrostatique, furtivité…), tenue à la corrosion, au feu, esthétique…

La modélisation aide à dimensionner le matériau en amont dans le développement d’un programme, soit en amont d’essais, soit pour économiser des essais. Plusieurs types de contraintes se prêtent bien à une modélisation de type physique, Passant par la résolution d’équations aux dérivées partielles : Mécanique, thermique, électromagnétique…

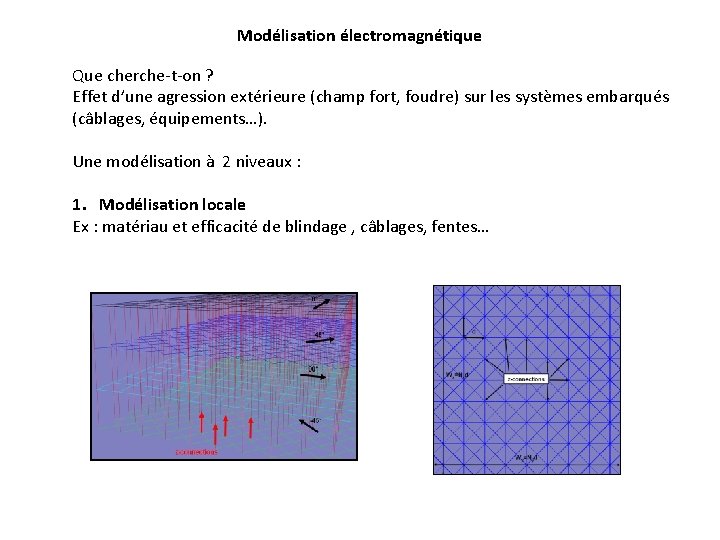
Modélisation électromagnétique Que cherche-t-on ? Effet d’une agression extérieure (champ fort, foudre) sur les systèmes embarqués (câblages, équipements…). Une modélisation à 2 niveaux : 1. Modélisation locale Ex : matériau et efficacité de blindage , câblages, fentes…

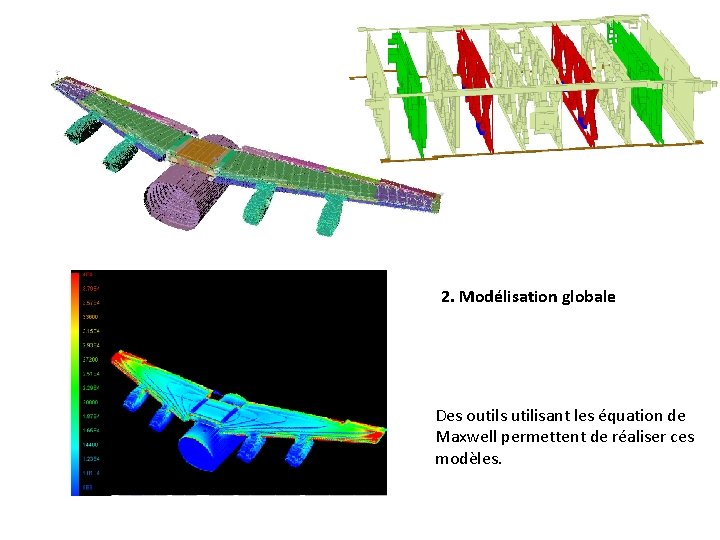
2. Modélisation globale Des outils utilisant les équation de Maxwell permettent de réaliser ces modèles.

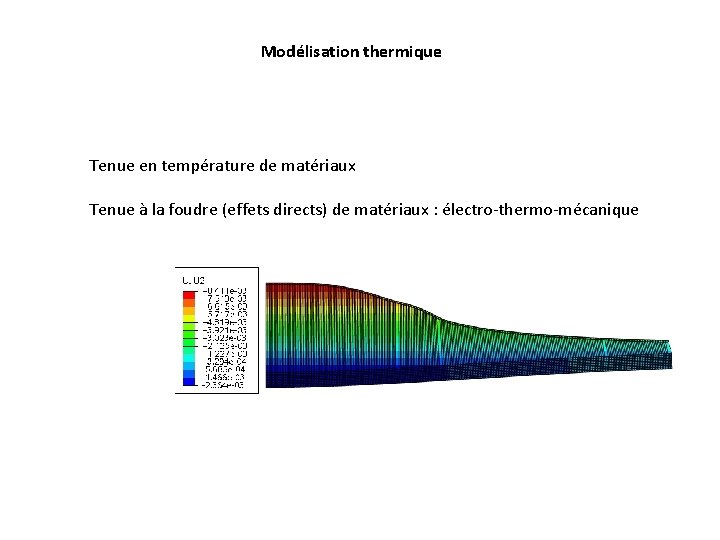
Modélisation thermique Tenue en température de matériaux Tenue à la foudre (effets directs) de matériaux : électro-thermo-mécanique

EQUATIONS DE MAXWELL E, H : champs D, B : inductions Conservation de la charge : Milieux linéaires : permittivité électrique perméabilité magnétique Loi d’Ohm : 11

Liens entre les différentes équations de Maxwell Je prends la divergence de l’équation de Faraday : Par ailleurs je prends la divergence de l’équation d’Ampère : Par comparaison avec l’équation de conservation de la charge : Conclusion : si à l’instant initial les champs satisfont : Et Alors à tout instant suivant, il suffit que les champs satisfassent les équations d’Ampère et de Faraday (et de conservation de la charge) pour satisfaire les autres équations de Maxwell. On ne propage numériquement que les équations de Faraday et Ampère. 12

Propagation dans un milieu conducteur Expulsion de la charge : Equations de propagation : Solution recherchée sous la forme : 13

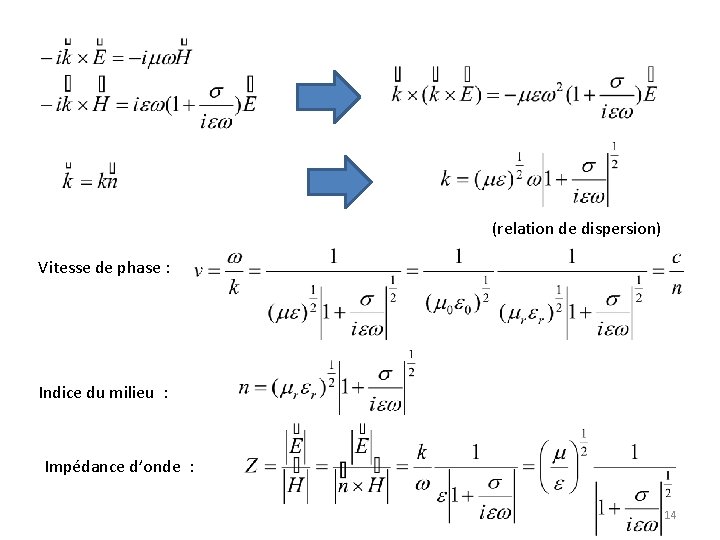
(relation de dispersion) Vitesse de phase : Indice du milieu : Impédance d’onde : 14

Cas particulier : mauvais conducteur : Vide (SI): Cas particulier : bon conducteur : δ : épaisseur de peau (décroit quand ω croit) : 15

Propagation avec atténuation : Exemples pour f=100 k. Hz (foudre…) : - Métal : σ=5 107 S/m δ≈0. 2 mm - Composite Carbone (CFC, CFRP…) σ= 104 S/m δ≈15 mm 16

Interfaces Discontinuités aux interfaces 1 2 n ρs (C/m 2) , Js (A/m): densités surfaciques 17

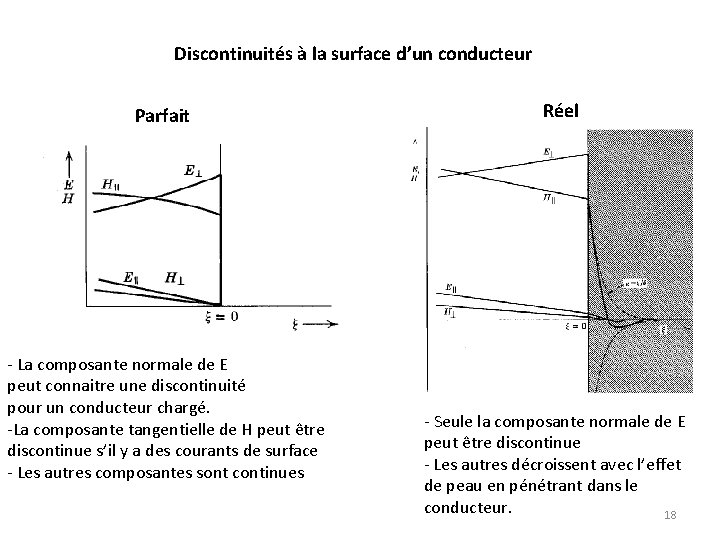
Discontinuités à la surface d’un conducteur Parfait - La composante normale de E peut connaitre une discontinuité pour un conducteur chargé. -La composante tangentielle de H peut être discontinue s’il y a des courants de surface - Les autres composantes sont continues Réel - Seule la composante normale de E peut être discontinue - Les autres décroissent avec l’effet de peau en pénétrant dans le conducteur. 18

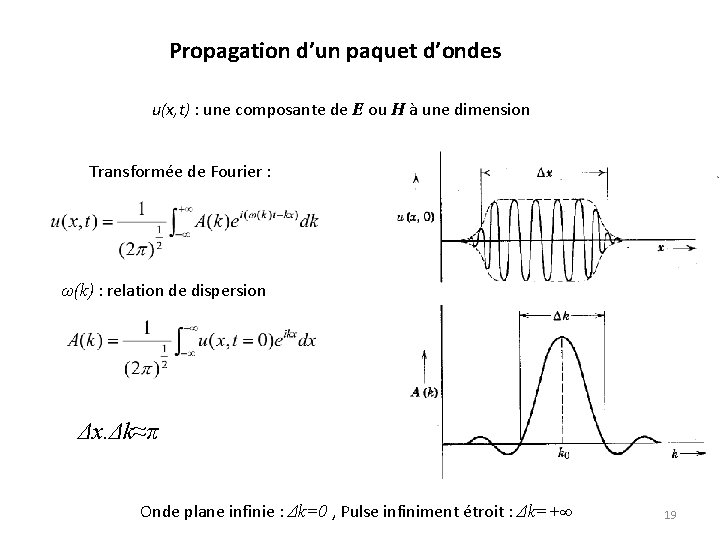
Propagation d’un paquet d’ondes u(x, t) : une composante de E ou H à une dimension Transformée de Fourier : ω(k) : relation de dispersion Δx. Δk≈π Onde plane infinie : Δk=0 , Pulse infiniment étroit : Δk=+∞ 19

Dispersion Supposons une loi de dispersion linéaire (vide, diélectrique…) : Le paquet d’onde se propage sans déformation à la vitesse de groupe : Dans le cas général (conducteur. . . ) la relation de dispersion n’est pas linéaire. Il y a donc déformation du paquet d’onde durant sa propagation. 20

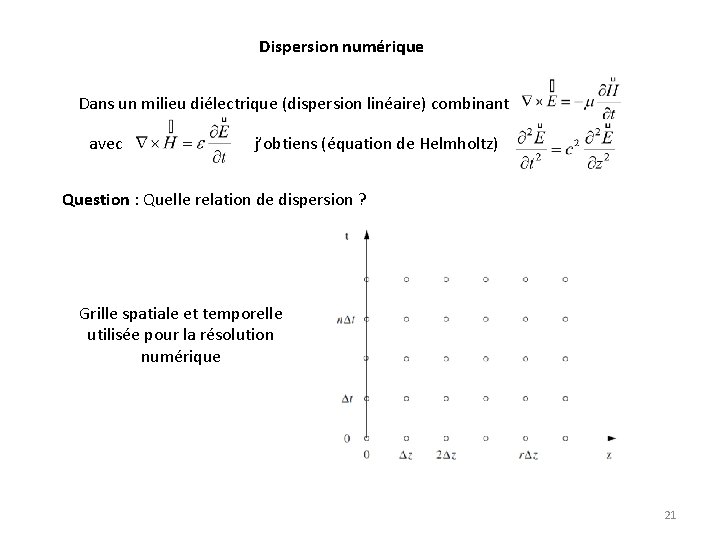
Dispersion numérique Dans un milieu diélectrique (dispersion linéaire) combinant avec j’obtiens (équation de Helmholtz) Question : Quelle relation de dispersion ? Grille spatiale et temporelle utilisée pour la résolution numérique 21

L’équation de Helmholtz, Pour une composante de champ, en différences finies, devient : Le champ à l’instant n+1 est donc donné par la récurrence : Je cherche la relation de dispersion que doit satisfaire une onde du type Pour être solution de l ’équation discrétisée Nouvelle relation de dispersion : QUESTION : Limite pour des intervalles tendant vers 0 ? 22

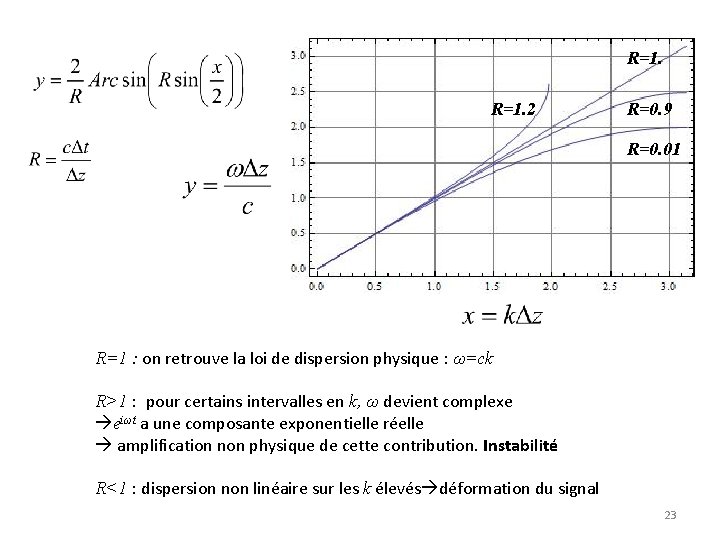
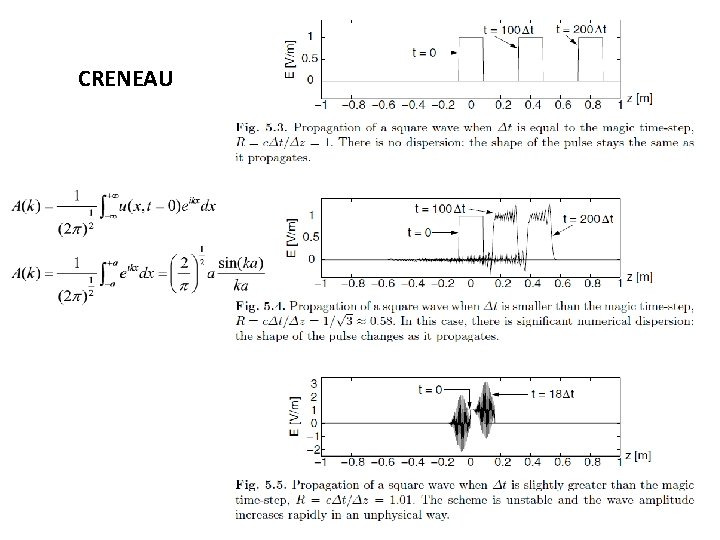
R=1. 2 R=0. 9 R=0. 01 R=1 : on retrouve la loi de dispersion physique : ω=ck R>1 : pour certains intervalles en k, ω devient complexe eiωt a une composante exponentielle réelle amplification non physique de cette contribution. Instabilité R<1 : dispersion non linéaire sur les k élevés déformation du signal 23

CRENEAU 24

PROPAGATION NUMERIQUE DES EQUATIONS DE MAXWELL CAS 1 D On ne propage que les eq. d’Ampère et Faraday 1 D Elles ont les 2 la même structure : Dérivée spatiale=dérivée temporelle Premières idées : 1. Différences finies centrées 2. Utiliser la même grille pour E et H (celle déjà utilisée). 25

Différences finies, grille unique Différences finies Au point (r, n) : Algorithme du type « saut de grenouille » (leapfrog) : je passe directement du temps n-1 au temps n+1 en passant par-dessus n. Inconvénient de l’algorithme : précision réduite du fait que, en temps comme en distance, On fait des sauts de 2 pas. En utilisant des grilles décalées (staggered) pour E et H, on peut réduire le saut à un seul pas ! 26

Différences finies, grilles décalées Grille Ex : (r, n) Grille Hy : (r+1/2, n+1/2) Au point (r, n+1/2) : Au point (r+1/2, n) : - Les sauts sont bien d’un seul pas - Les points où sont utilisées les équations n’appartiennent ni à la grille E, ni à la grille H - QUESTION : quelle relation de dispersion ? 27

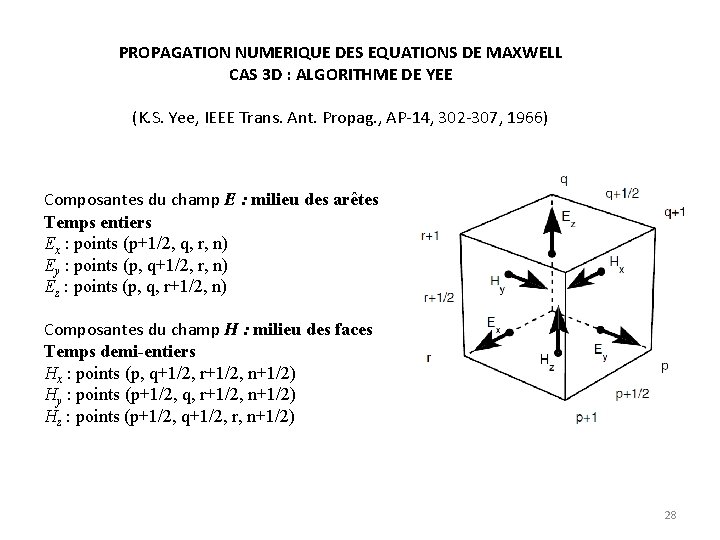
PROPAGATION NUMERIQUE DES EQUATIONS DE MAXWELL CAS 3 D : ALGORITHME DE YEE (K. S. Yee, IEEE Trans. Ant. Propag. , AP-14, 302 -307, 1966) Composantes du champ E : milieu des arêtes Temps entiers Ex : points (p+1/2, q, r, n) Ey : points (p, q+1/2, r, n) Ez : points (p, q, r+1/2, n) Composantes du champ H : milieu des faces Temps demi-entiers Hx : points (p, q+1/2, r+1/2, n+1/2) Hy : points (p+1/2, q, r+1/2, n+1/2) Hz : points (p+1/2, q+1/2, r, n+1/2) 28

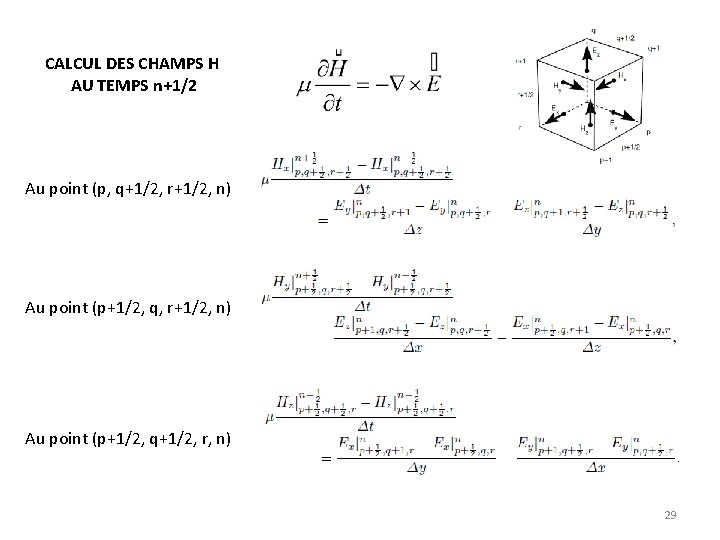
CALCUL DES CHAMPS H AU TEMPS n+1/2 Au point (p, q+1/2, r+1/2, n) Au point (p+1/2, q+1/2, r, n) 29

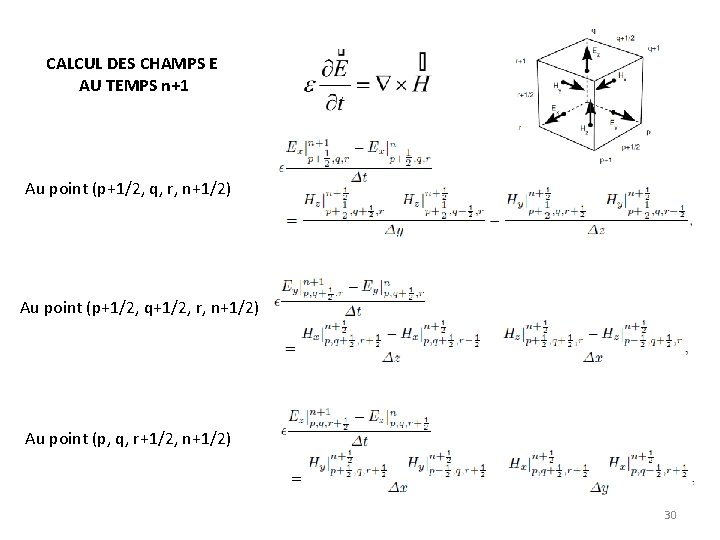
CALCUL DES CHAMPS E AU TEMPS n+1 Au point (p+1/2, q, r, n+1/2) Au point (p+1/2, q+1/2, r, n+1/2) Au point (p, q, r+1/2, n+1/2) 30

ALGORITHME DE YEE : RELATION DE DISPERSION 3 D Quelle relation ω(k) pour avoir une solution du type Expressions des opérateurs différentiels Si f(x)=e i(ωt-kx) alors 31

Alors les équations de Yee donnent : Si Combinant ces 2 équations : donc Par ailleurs Donc Résultat Relation de dispersion 3 D 32

Condition de stabilité : Qui est satisfaite si : Condition CFL (Courant-Friedrichs-Levy) : 33

Choix de la taille de maille : - Description suffisamment précise des détails géométriques - Critère de longueur d’onde ≈ 10 points par longueur d’onde Choix du pas de temps : critère CFL Occupation mémoire : (2 pas de temps stockés)*(6 composantes)*Nx. Ny. Nz=12 Nx. Ny. Nz Temps de calcul : proportionnel à 6 Nx. Ny. Nz. Nt Proportionnel à (fréquence)**4 Impossibilité pratique du calcul à très hautes fréquences : autres méthodes (asymptotiques : optique, théorie de rayons…) 34

Exemple : on veut modéliser un avion. Taille : 50 m. On considère un coup de foudre qui dure 100 μs. On veut représenter de façon suffisamment fine les détails taille de maille : 0. 1 m Nombre de mailles ≈ 10003=109 (en fait on a moins besoin pour la hauteur) soit 12*8=96 Go d’occupation mémoire Pas de temps max : Δx/31/2 c≈0. 2 ns, soit Nt=500 000 Nombre d’opérations : de l’ordre de 6*500 000*109=3 1015 Temps de calcul sur un processeur à 30 Gflops : 105 s ≈ la journée Fréquence max traitée correctement dans ce calcul : longueur d’onde = (10 points par longueur d’onde)*0. 1 m=1 m, soit 300 MHz. 35

Limitations du volume maillé Il faut absorber l’onde en bords de volume. Si on mettait un conducteur (effet de peau…) il y aurait des réflexions très importantes. On ajoute une couche absorbante de matériaux fictifs (conductivité magnétique !) en bords de volume Impédance d’onde : (cf page 14) Pour une onde normale à la surface le coefficient de réflexion est : Si Z=Z 0 : pas de réflexion ! Adaptation d’impédance On obtient cette adaptation d’impédance si : 36

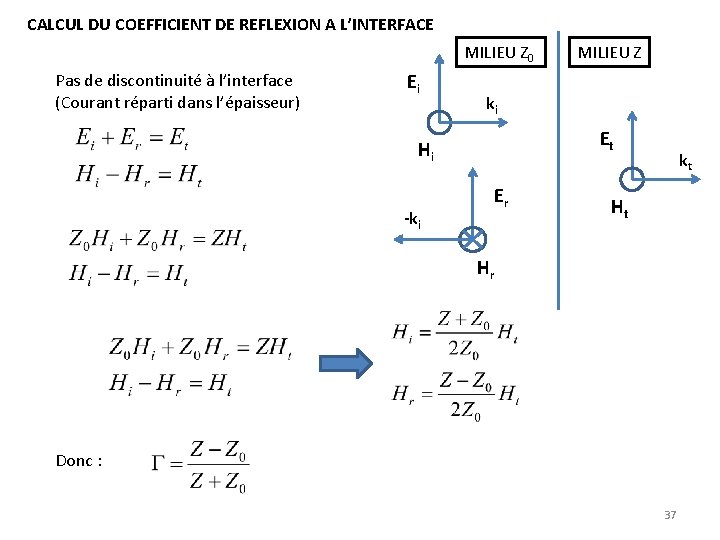
CALCUL DU COEFFICIENT DE REFLEXION A L’INTERFACE MILIEU Z 0 Pas de discontinuité à l’interface (Courant réparti dans l’épaisseur) Ei ki Et Hi -ki MILIEU Z Er kt Ht Hr Donc : 37

Cas général : onde incidente non normale J. P. Bérenger, J. Comput. Phys. 114, 185 (1994) Séparer les composantes du champ parallèle à la couche absorbante en 2 morceaux (ici, la couche absorbante en perpendiculaire à z) Quand σ=σ*=0, on retrouve les équations dans le milieu physique. Seule les morceaux en z (cad correspondant à une propagation en z) sont modifiés. La propagation en x, y est inchangée. 38

Dans la pratique, il faut considérer des murs perpendiculaires à x, y , z. …et il faut augmenter progressivement les conductivités, par exemple : 39

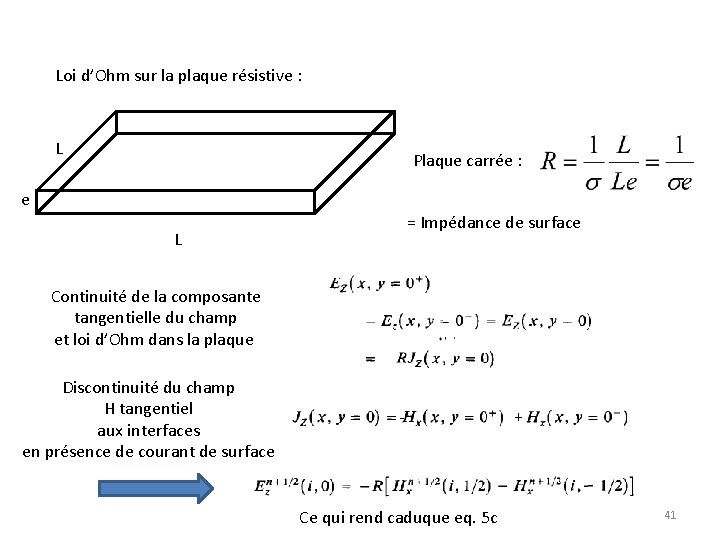
Plaques minces : cas 2 D (pour simplifier) L. K. Wu et L. T. Han, IEEE Transactions on Antennas and Propagation, vol. 40, 628, 1992 On ne veut pas mailler l’épaisseur de la plaque, cela conduirait à des maillages énormes ! On remplace la plaque par une résistance équivalente modèle basse fréquence (pas d’effet de peau = pas d’induction) Pas de dépendance en z Question : S 1, S 2 ? 40

Loi d’Ohm sur la plaque résistive : L Plaque carrée : e = Impédance de surface L Continuité de la composante tangentielle du champ et loi d’Ohm dans la plaque Discontinuité du champ H tangentiel aux interfaces en présence de courant de surface - Ce qui rend caduque eq. 5 c + 41

Algorithme initial Algorithme modifié sur la plaque 2 R En supposant une dépendance linéaire en temps autour de n+1/2 42

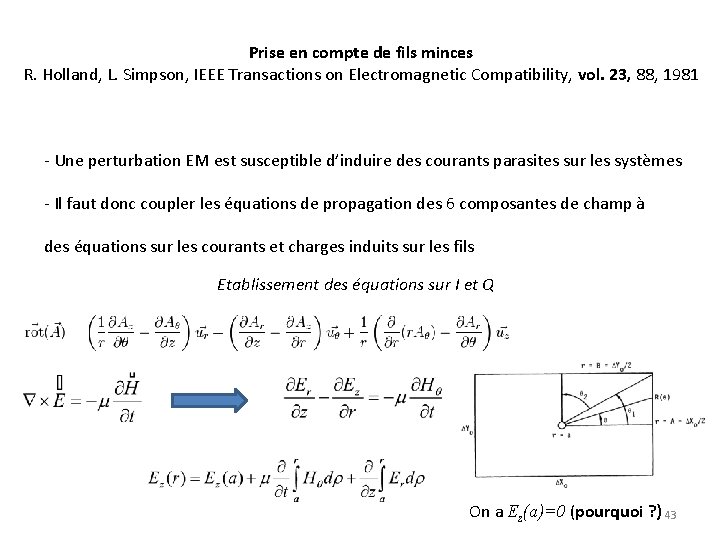
Prise en compte de fils minces R. Holland, L. Simpson, IEEE Transactions on Electromagnetic Compatibility, vol. 23, 88, 1981 - Une perturbation EM est susceptible d’induire des courants parasites sur les systèmes - Il faut donc coupler les équations de propagation des 6 composantes de champ à des équations sur les courants et charges induits sur les fils Etablissement des équations sur I et Q On a Ez(a)=0 (pourquoi ? ) 43

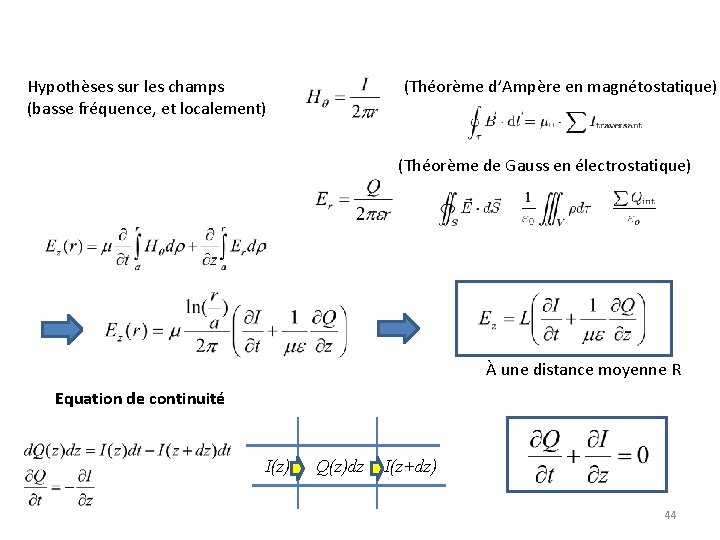
Hypothèses sur les champs (basse fréquence, et localement) (Théorème d’Ampère en magnétostatique) (Théorème de Gauss en électrostatique) À une distance moyenne R Equation de continuité I(z) Q(z)dz I(z+dz) 44

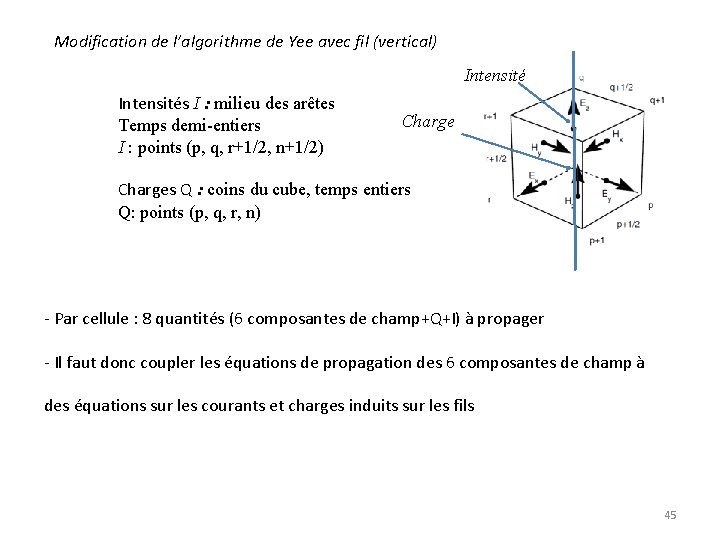
Modification de l’algorithme de Yee avec fil (vertical) Intensités I : milieu des arêtes Temps demi-entiers I : points (p, q, r+1/2, n+1/2) Charges Q : coins du cube, temps entiers Q: points (p, q, r, n) - Par cellule : 8 quantités (6 composantes de champ+Q+I) à propager - Il faut donc coupler les équations de propagation des 6 composantes de champ à des équations sur les courants et charges induits sur les fils 45

Modification de l’algorithme de Yee avec fils 1. Calculer I au temps n+1/2, à partir de I au temps n-1/2 et de E et de Q au temps n 2. Calculer H au temps n+1/2, à partir de H au temps n-1/2 et de E au temps n 3. Calculer E au temps n+1, à partir de E au temps n et de H et de I au temps n+1/2 Yee sans changement Yee avec rajout du courant du fil 46 4. Calculer Q au temps n+1, à partir de Q au temps n et de I au temps n+1/2