Section VII The Standard Model The Standard Model






























- Slides: 48

Section VII The Standard Model

The Standard Model Spin ½ Fermions Charge (units of e) -1 0 LEPTONS QUARKS 2/3 -1/3 PLUS antileptons and antiquarks. Spin 1 Bosons Gluon Photon W and Z Bosons g g W , Z 0 Mass (Ge. V/c 2) 0 0 91. 2/80. 3 STRONG EM WEAK The Standard Model also predicts the existence of a spin 0 HIGGS BOSON which gives all particles their masses via its interactions. 201

Theoretical Framework Slow Macroscopic Classical Mechanics Fast Special Relativity Microscopic Quantum Mechanics Quantum Field Theory The Standard Model is a collection of related GAUGE THEORIES which are QUANTUM FIELD THEORIES that satisfy LOCAL GAUGE INVARIANCE. ELECTROMAGNETISM: QUANTUM ELECTRODYNAMICS (QED) 1948 Feynman, Schwinger, Tomonaga (1965 Nobel Prize) ELECTROMAGNETISM: ELECTROWEAK UNIFICATION +WEAK 1968 Glashow, Weinberg, Salam (1979 Nobel Prize) STRONG: QUANTUM CHROMODYNAMICS (QCD) 1974 Politzer, Wilczek, Gross (2004 Nobel Prize) 202

ASIDE : Relativistic Kinematics ØLow energy nuclear reactions take place with typical kinetic energies of order 10 Me. V << nucleon rest energies ) non-relativistic formulae OK. ØIn particle physics kinetic energy is of O (100 Ge. V) >> rest mass energies so relativistic formulae usually essential. § Always treat -decay relativisticly (me ~ 0. 5 Me. V < 1. 3 Me. V ~ mn-mp). ØWE WILL ASSUME UNDERSTANDING OF FOUR VECTORS and FOUR MOMENTA from the Part II Relativity Electrodynamics and Light course. . . in natural units: § Definitions: mass = m velocity= v = βc(= β) mom = p § Consequences: 203

ASIDE cont: (Decay example) Consider decay of charged pion at rest in the lab frame Conservation of Energy and Momentum says: Appropriate choice of axes gives, and noting pion is at rest (pπ=0) gives: So have two simultaneous equations in two unknowns & . Once you know p you know E etc via etc …. (Simplify by taking mν=0 ) 204

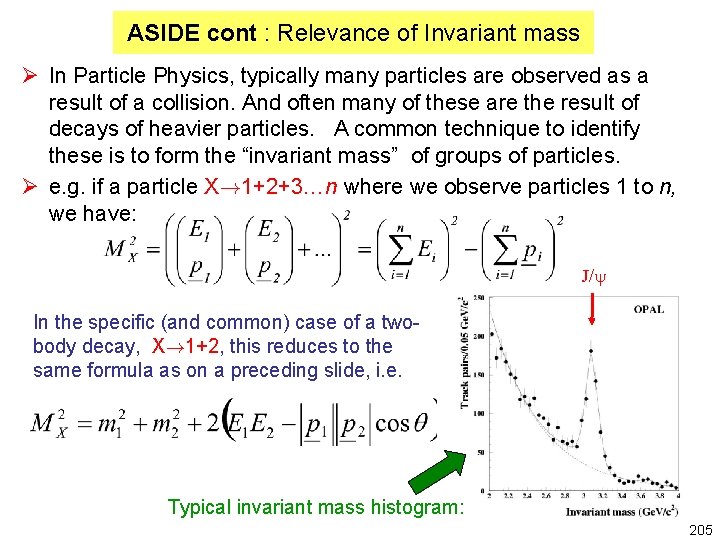
ASIDE cont : Relevance of Invariant mass Ø In Particle Physics, typically many particles are observed as a result of a collision. And often many of these are the result of decays of heavier particles. A common technique to identify these is to form the “invariant mass” of groups of particles. Ø e. g. if a particle X!1+2+3…n where we observe particles 1 to n, we have: J/y In the specific (and common) case of a twobody decay, X!1+2, this reduces to the same formula as on a preceding slide, i. e. Typical invariant mass histogram: 205

ASIDE cont : Colliders and √s Consider the collision of two particles: The invariant quantity is the angle between the momentum three-vectors is the energy in the zero momentum (centre-of-mass) frame; It is the amount of energy available to the interaction e. g. in particleantiparticle annihilation it is the maximum energy/mass of particle(s) that can be produced 206

Fixed Target Collision For e. g. 450 Ge. V proton hitting a proton at rest: Collider Experiment For then and = e. g. 450 Ge. V proton colliding with a 450 Ge. V proton: In a fixed target experiment most of the proton’s energy is wasted providing forward momentum to the final state particles rather than being available for conversion into interesting particles. 207

ASIDE over Back to the main topic of combining Quantum Mechanics with Special Relativity…. . 208

Problems with Non-Relativistic Schrodinger Equation To describe the fundamental interactions of particles we need a theory of RELATIVISTIC QUANTUM MECHANICS. Schrodinger Equation for a free particle comes from classical or equivalently promoted to an operator equation using energy and momentum operators: giving ħ =1 natural units which has plane wave solutions: Schrodinger Equation: Ø 1 st Order in time derivative Not Lorentz Invariant! nd Ø 2 Order in space derivatives Schrodinger equation cannot be used to describe the physics of relativistic particles. 209

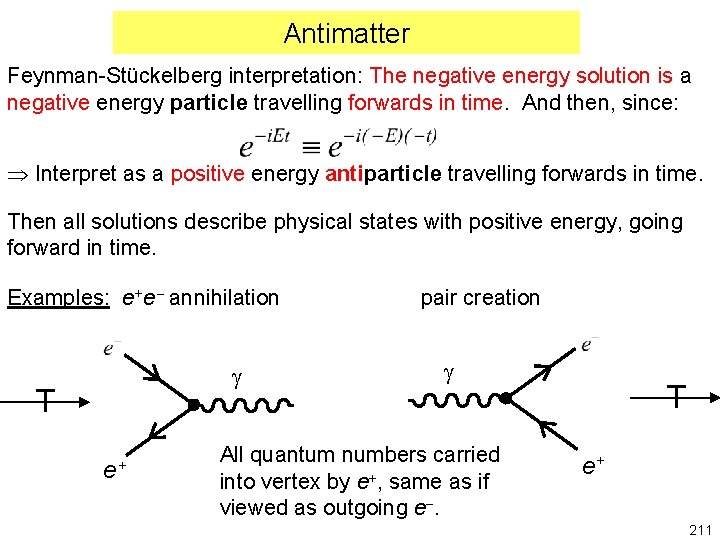
Klein-Gordon Equation (relativistic) From Special Relativity: From Quantum Mechanics: Combine to give: KLEIN-GORDON EQUATION Second order in both space and time derivatives and hence Lorentz invariant. Again plane wave solutions but this time requiring allowing Negative energy solutions required to form complete set of eigenstates ANTIMATTER 210

Antimatter Feynman-Stückelberg interpretation: The negative energy solution is a negative energy particle travelling forwards in time. And then, since: Interpret as a positive energy antiparticle travelling forwards in time. Then all solutions describe physical states with positive energy, going forward in time. Examples: e+e annihilation g T e+ pair creation g All quantum numbers carried into vertex by e+, same as if viewed as outgoing e-. T e+ 211

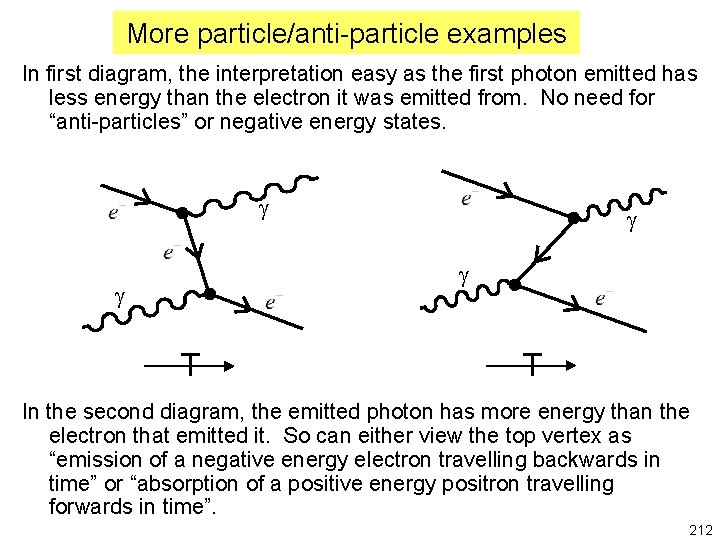
More particle/anti-particle examples In first diagram, the interpretation easy as the first photon emitted has less energy than the electron it was emitted from. No need for “anti-particles” or negative energy states. g g T T In the second diagram, the emitted photon has more energy than the electron that emitted it. So can either view the top vertex as “emission of a negative energy electron travelling backwards in time” or “absorption of a positive energy positron travelling forwards in time”. 212

Normalization Can show solutions of Schrodinger Equation (non-relativistic) satisfy: and solutions of Klein-Gordon Equation (relativistic) satisfy: Both are of the form: and the divergence theorem tells us that this means that D is conserved, where: If we interpret D as number of particles, and as number of particles per unit volume, then: For plane wave of arbitrary normalization find that: Non-relativistic: particles per unit volume. Relativistic: particles per unit volume. 213

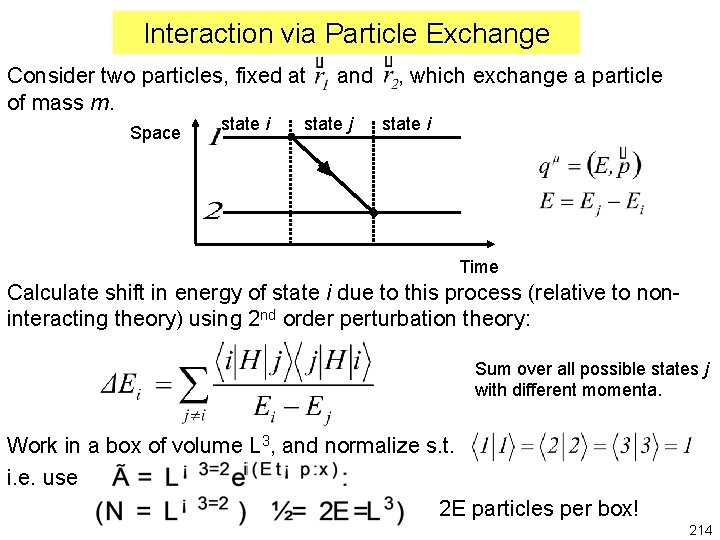
Interaction via Particle Exchange Consider two particles, fixed at of mass m. Space state i and state j , which exchange a particle state i Time Calculate shift in energy of state i due to this process (relative to noninteracting theory) using 2 nd order perturbation theory: Sum over all possible states j with different momenta. Work in a box of volume L 3, and normalize s. t. i. e. use 2 E particles per box! 214

Consider ( transition from i to j by emission of m at ) Original 2 particles represents a free particle with Let g be the “strength” of the emission at Similarly . Then: is the transition from j to i at and is Substituting these in, we see the shift in energy state is 215

Normalization of source strength “g” for relativistic situations Previously normalized wave-functions to 1 particle in a box of side L. In relativity, the box will be Lorentz contracted by a factor g Rest frame 1 particle per V Lab. frame 1 particle per V/g i. e. particles per volume V. (Proportional to 2 E particles per unit volume as we already saw a few slides back) Need to adjust “g” with energy (next year you will see “g” is “lorentz invariant” matrix element for interaction) Conventional choice: (square root as g always occurs squared) Source “appears” lorentz contracted to particles of high energy, and effective coupling must decrease to compensate. The presence of the E is important. The presence of the 2 is just convention. The absence of the m (in gamma) is just a convention to keep g dimensionless here. 216

Beginning to put it together Different states j have different momenta an integral over all momenta: . Therefore sum is actually And so energy change: 217

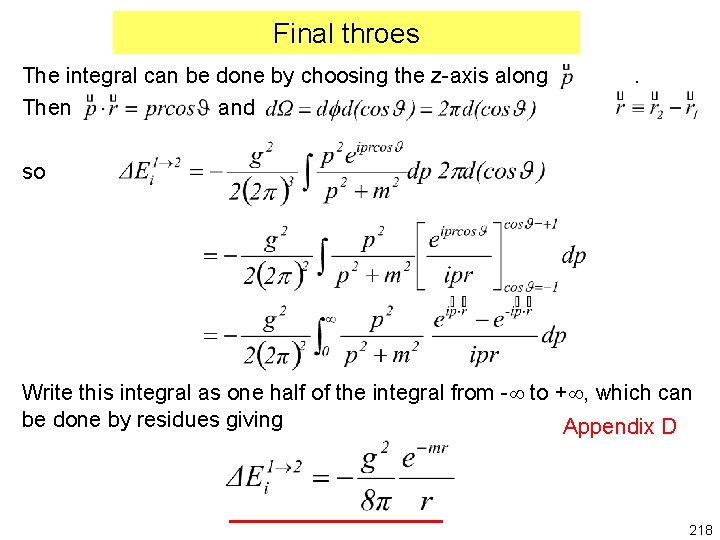
Final throes The integral can be done by choosing the z-axis along Then and . so Write this integral as one half of the integral from - to + , which can be done by residues giving Appendix D 218

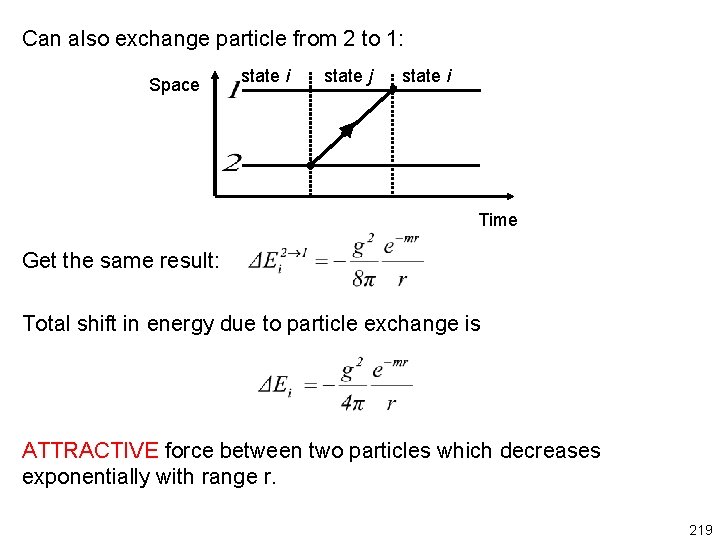
Can also exchange particle from 2 to 1: Space state i state j state i Time Get the same result: Total shift in energy due to particle exchange is ATTRACTIVE force between two particles which decreases exponentially with range r. 219

Yukawa Potential YUKAWA POTENTIAL Ø Characteristic range = 1/m (Compton wavelength of exchanged particle) Ø For m 0, Hideki Yukawa 1949 Nobel Prize infinite range Yukawa potential with m = 139 Me. V/c 2 gives good description of long range interaction between two nucleons and was the basis for the prediction of the existence of the pion. 220

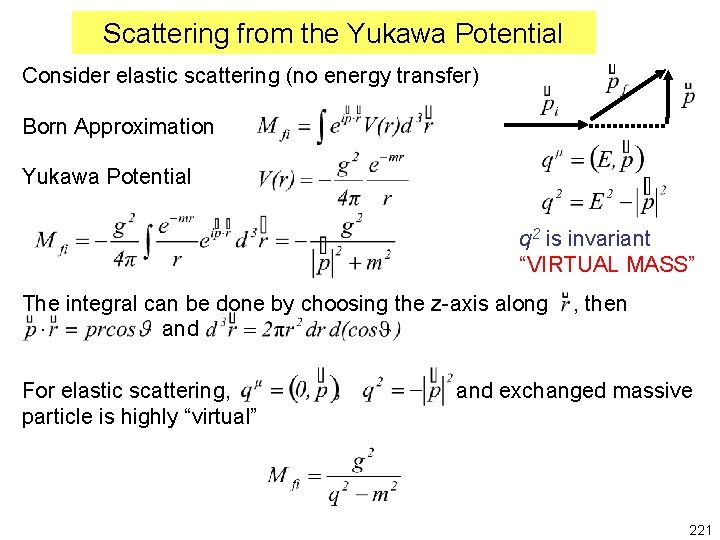
Scattering from the Yukawa Potential Consider elastic scattering (no energy transfer) Born Approximation Yukawa Potential q 2 is invariant “VIRTUAL MASS” The integral can be done by choosing the z-axis along and For elastic scattering, particle is highly “virtual” , then and exchanged massive 221

Virtual Particles Forces arise due to the exchange of unobservable VIRTUAL particles. Ø The mass of the virtual particle, q 2, is given by and is not the physical mass m, i. e. it is OFF MASS-SHELL. Ø The mass of a virtual particle can by +ve, -ve or imaginary. Ø A virtual particle which is off-mass shell by amount Dm can only exist for time and range ħ =c=1 natural units Ø If q 2 = m 2, then the particle is real and can be observed. 222

For virtual particle exchange, expect a contribution to the matrix element of where COUPLING CONSTANT STRENGTH OF INTERACTION PHYSICAL (On-shell) mass VIRTUAL (Off-shell) mass PROPAGATOR Qualitatively: the propagator is inversely proportional to how far the particle is off-shell. The further off-shell, the smaller the probability of producing such a virtual state. Ø For m 0 ; e. g. single g exchange Ø q 2 0, very low energy transfer EM scattering 223

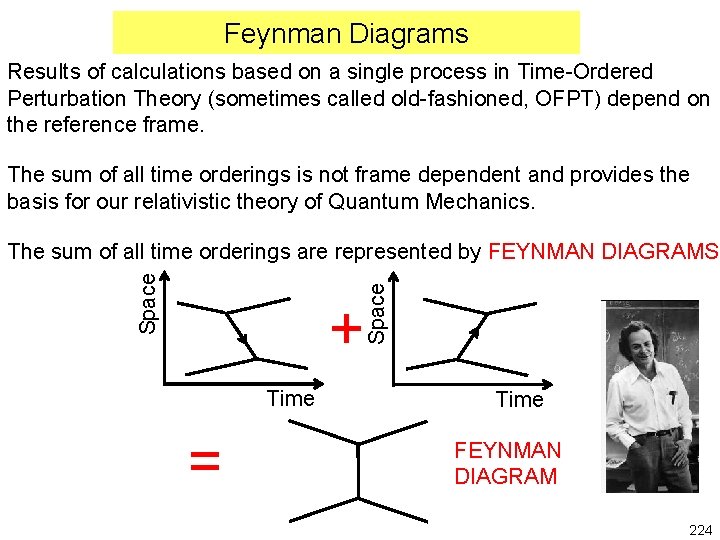
Feynman Diagrams Results of calculations based on a single process in Time-Ordered Perturbation Theory (sometimes called old-fashioned, OFPT) depend on the reference frame. The sum of all time orderings is not frame dependent and provides the basis for our relativistic theory of Quantum Mechanics. Space The sum of all time orderings are represented by FEYNMAN DIAGRAMS. + Time = Time FEYNMAN DIAGRAM 224

Feynman diagrams represent a term in the perturbation theory expansion of the matrix element for an interaction. Normally, a matrix element contains an infinite number of Feynman diagrams. Total amplitude Total rate Fermi’s Golden Rule But each vertex gives a factor of g, so if g is small (i. e. the perturbation is small) only need the first few. Example: QED 225

Anatomy of Feynman Diagrams Feynman devised a pictorial method for evaluating matrix elements for the interactions between fundamental particles in a few simple rules. We shall use Feynman diagrams extensively throughout this course. Represent particles (and antiparticles): Spin ½ Quarks and Leptons Spin 1 g, W and Z 0 g and their interaction point (vertex) with a “ “. Each vertex gives a factor of the coupling constant, g. 226

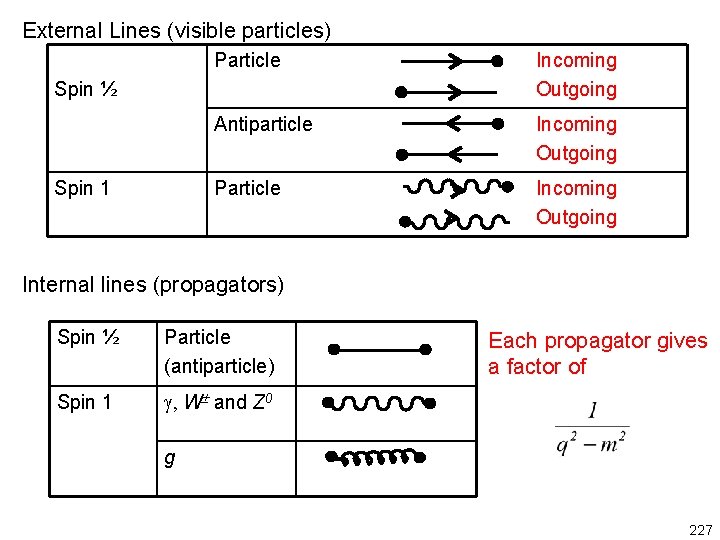
External Lines (visible particles) Particle Incoming Outgoing Antiparticle Incoming Outgoing Particle Incoming Outgoing Spin ½ Spin 1 Internal lines (propagators) Spin ½ Particle (antiparticle) Spin 1 g, W and Z 0 Each propagator gives a factor of g 227

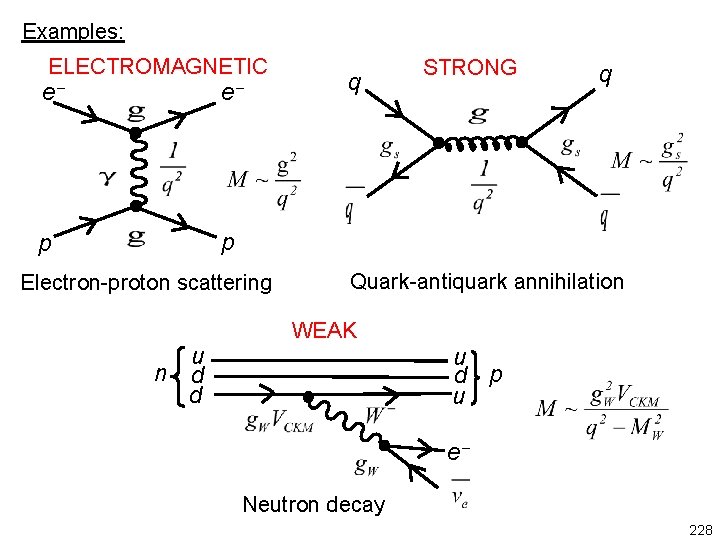
Examples: ELECTROMAGNETIC e e p p Electron-proton scattering u n d d q STRONG q Quark-antiquark annihilation WEAK u d p u e Neutron decay 228

Summary Ø Relativistic mechanics necessary for most calculations involving Particle Physics and the Standard Model § Anti-particles arise from requiring wave equation be relativistically invariant Ø Calculating Matrix Elements from Perturbation Theory from first principles is a pain – so we don’t usually use it! § Need to do time-ordered sums of (on mass shell) particles whose production and decay does not conserve energy and momentum ! Ø Feynman Diagrams / Rules manage to represent the maths of Perturbation Theory (to arbitrary order, if couplings are small enough) in a very simple way – so we use them to calculate matrix elements! § Approx size of matrix element may be estimated from the simplest valid Feynman Diagram for given process. § Full matrix element requires infinite number of diagrams. § Now only need one exchanged particle, but it is now off mass shell, however production/decay now conserves energy and momentum. 229

Section VIII QED

QED QUANTUM ELECTRODYNAMICS is the gauge theory of electromagnetic interactions. Consider a non-relativistic charged particle in an EM field: given in term of vector and scalar potentials Maxwell’s Equations g Change in state of e- requires change in field Interaction via virtual g emission 231

Schrodinger equation is invariant under the gauge transformation Appendix E LOCAL GAUGE INVARIANCE requires a physical GAUGE FIELD (photon) and completely specifies the form of the interaction between the particle and field. Ø Photons (all gauge bosons) are intrinsically massless (though gauge bosons of the Weak Force evade this requirement by “symmetry breaking”) Ø Charge is conserved – the charge q which interacts with the field must not change in space or time. DEMAND that QED be a GAUGE THEORY 232

The Electromagnetic Vertex All electromagnetic interactions can be described by the photon propagator and the EM vertex: g STANDARD MODEL ELECTROMAGNETIC VERTEX +antiparticles Ø The coupling constant, g, is proportional to the fermion charge. Ø Energy, momentum, angular momentum and charge always conserved. Ø QED vertex NEVER changes particle type or flavour i. e. but not or Ø QED vertex always conserves PARITY 233

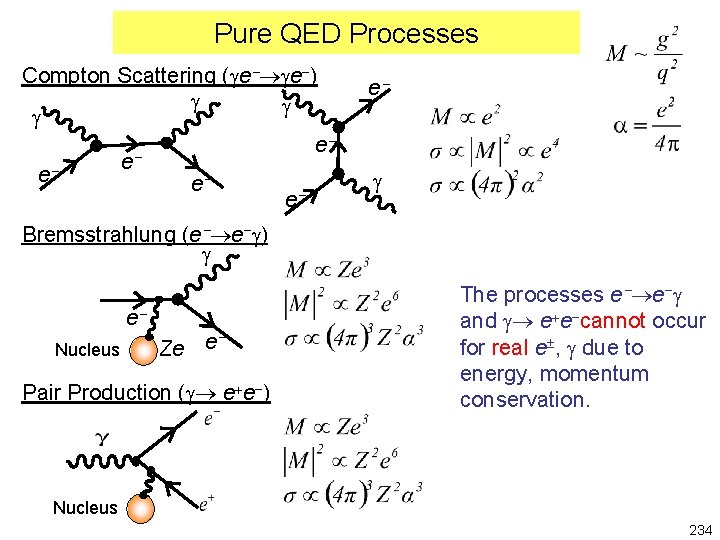
Pure QED Processes Compton Scattering (ge ge-) g g g e e e e g Bremsstrahlung (e e-g) g e Nucleus e Ze Pair Production (g e+e-) The processes e e-g and g e+e-cannot occur for real e , g due to energy, momentum conservation. Nucleus 234

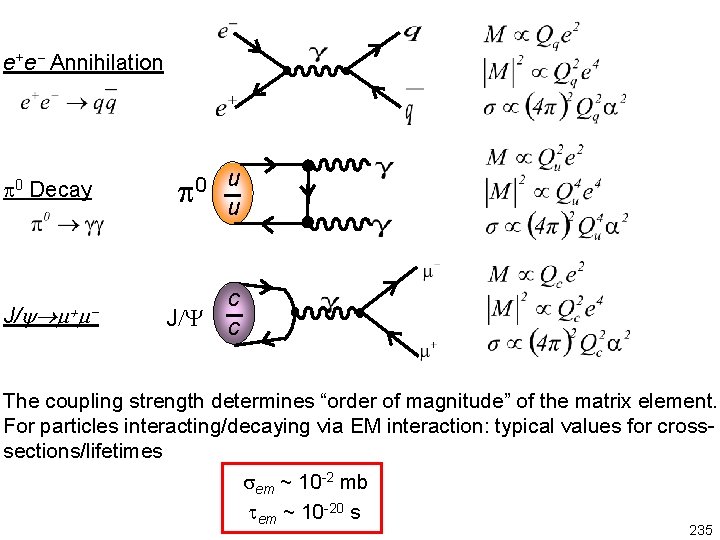
e+e Annihilation 0 Decay J/ + u 0 u J/Y c c The coupling strength determines “order of magnitude” of the matrix element. For particles interacting/decaying via EM interaction: typical values for crosssections/lifetimes sem ~ 10 -2 mb tem ~ 10 -20 s 235

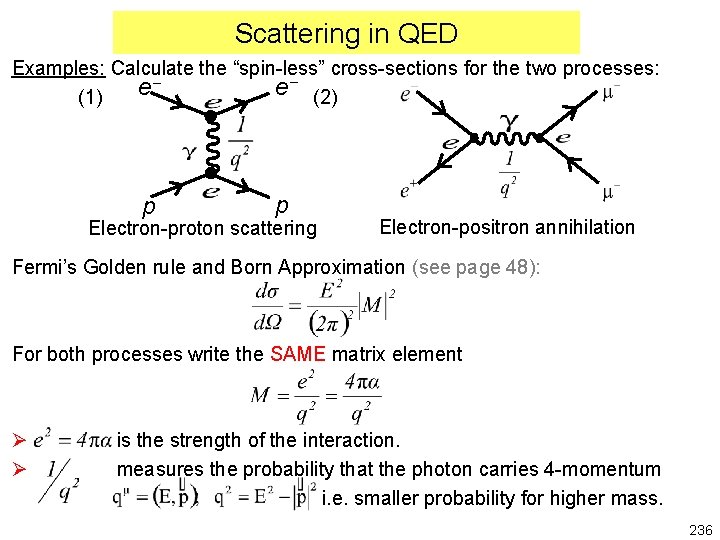
Scattering in QED Examples: Calculate the “spin-less” cross-sections for the two processes: e e (1) (2) p p Electron-proton scattering Electron-positron annihilation Fermi’s Golden rule and Born Approximation (see page 48): For both processes write the SAME matrix element Ø Ø is the strength of the interaction. measures the probability that the photon carries 4 -momentum i. e. smaller probability for higher mass. 236

(1) “Spin-less” e-p Scattering e e p p q 2 is the four-momentum transfer: e e Neglecting electron mass: i. e. and Therefore for ELASTIC scattering RUTHERFORD SCATTERING 237

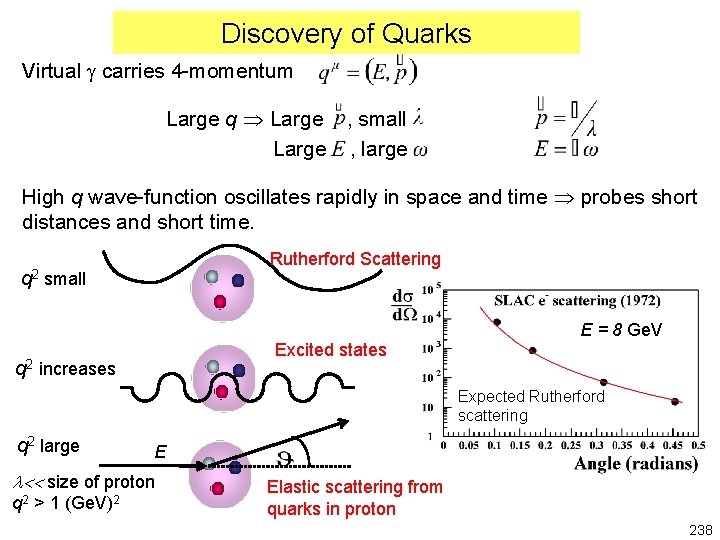
Discovery of Quarks Virtual g carries 4 -momentum Large q Large , small Large , large High q wave-function oscillates rapidly in space and time probes short distances and short time. q 2 Rutherford Scattering small Excited states q 2 increases E = 8 Ge. V Expected Rutherford scattering q 2 large E l<< size of proton q 2 >1 (Ge. V)2 Elastic scattering from quarks in proton 238

(2) “Spin-less” e+e- Annihilation Same formula, but different 4 -momentum transfer: Assuming we are in the centre-of-mass system Integrating gives total cross-section: 239

This is not quite correct, because we have neglected spin. The actual cross-section (using the Dirac equation) is Example: Cross-section at Ge. V (i. e. 11 Ge. V electrons colliding with 11 Ge. V positrons) 240

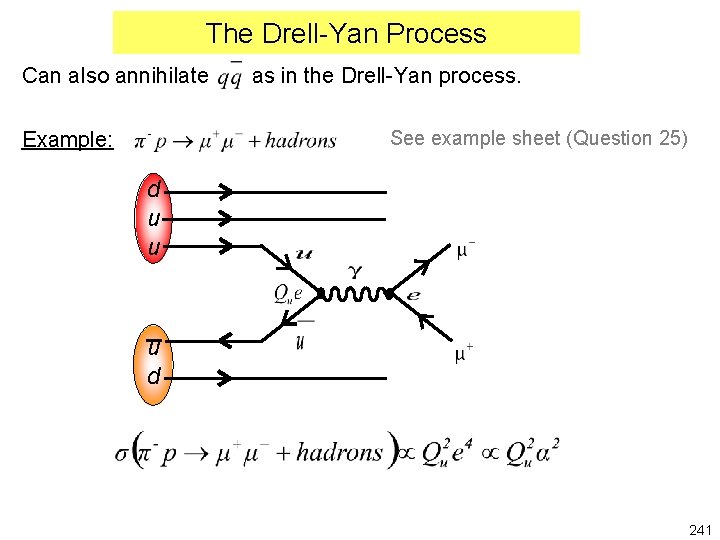
The Drell-Yan Process Can also annihilate as in the Drell-Yan process. See example sheet (Question 25) Example: d u u u d 241

Experimental Tests of QED is an extremely successful theory tested to very high precision. Example: Ø Magnetic moments of e , : Ø For a point-like spin ½ particle: Dirac Equation However, higher order terms introduce an anomalous magnetic moment i. e. g not quite 2. v v O(1) O( ) O( 4) 12672 diagrams 242

O( 3) Experiment Theory Ø Agreement at the level of 1 in 108. Ø QED provides a remarkable precise description of the electromagnetic interaction ! 243

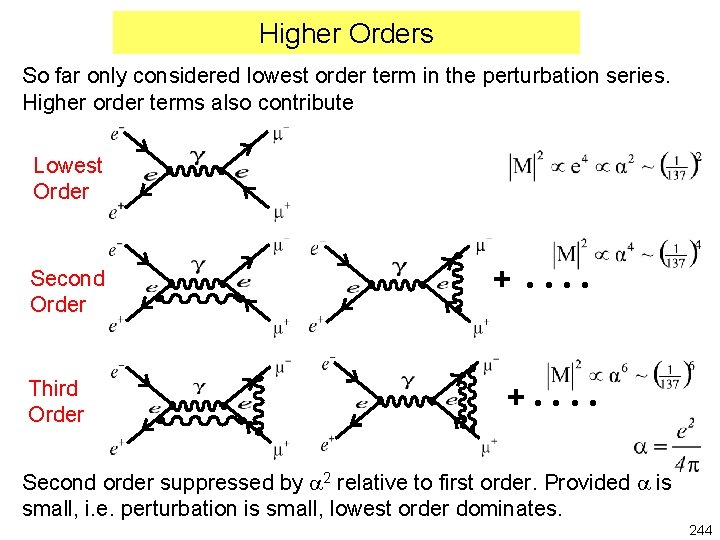
Higher Orders So far only considered lowest order term in the perturbation series. Higher order terms also contribute Lowest Order Second Order Third Order + + Second order suppressed by 2 relative to first order. Provided is small, i. e. perturbation is small, lowest order dominates. 244

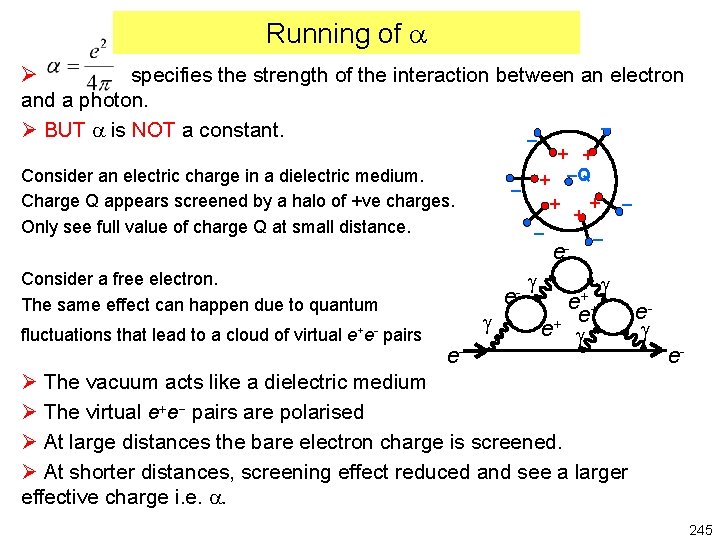
Running of Ø specifies the strength of the interaction between an electron and a photon. Ø BUT is NOT a constant. + + + -Q + + + - Consider an electric charge in a dielectric medium. Charge Q appears screened by a halo of +ve charges. Only see full value of charge Q at small distance. - e Consider a free electron. The same effect can happen due to quantum fluctuations that lead to a cloud of virtual e+e- pairs g e- e- g e+ e+ g eg e- Ø The vacuum acts like a dielectric medium Ø The virtual e+e- pairs are polarised Ø At large distances the bare electron charge is screened. Ø At shorter distances, screening effect reduced and see a larger effective charge i. e. . 245

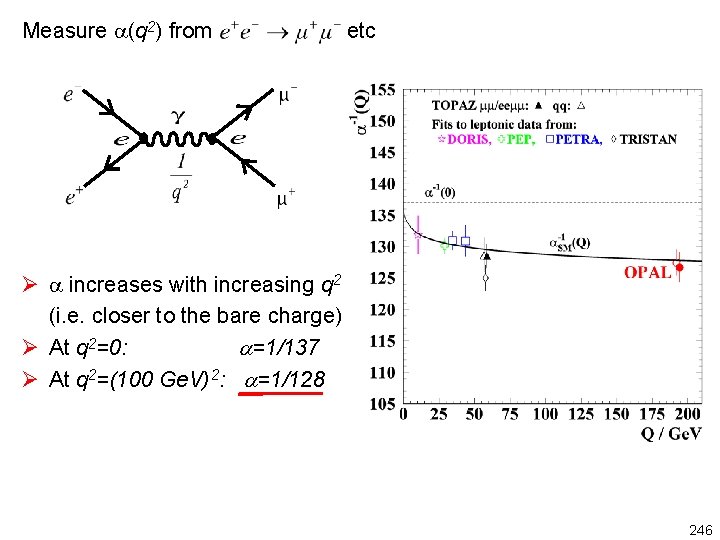
Measure (q 2) from etc Ø increases with increasing q 2 (i. e. closer to the bare charge) Ø At q 2=0: a=1/137 Ø At q 2=(100 Ge. V)2: a=1/128 246

Summary Ø QED is the physics of the photon + “charged particle” vertex: g Ø Every Feynman vertex has: § § § An arrow going in (lepton or quark) An arrow going out (lepton or quark) And a photon Does not change the type of lepton or quark “passing through” Conserves charge, energy and momentum. Ø The coupling α “runs”, and is proportional to the electric charge of the lepton or quark Ø QED has been tested at the level of 1 part in 108. 247
 Hexacarbon decahydride formula
Hexacarbon decahydride formula Fernando vii
Fernando vii Reach annex vii testing
Reach annex vii testing O vino iar in al meu brat
O vino iar in al meu brat Pedagogika tarixi pdf
Pedagogika tarixi pdf Light bulb types
Light bulb types Pasari acarenate
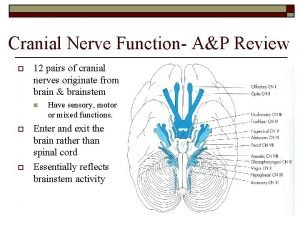
Pasari acarenate Cranial nerves smile
Cranial nerves smile Cn 8 test
Cn 8 test Henryk vii tudor
Henryk vii tudor Inmultirea la animale
Inmultirea la animale Monarchs of england
Monarchs of england Henry viii family tree
Henry viii family tree 100 people surveyed
100 people surveyed Lettera vii platone
Lettera vii platone Nerf 7 bis
Nerf 7 bis Song vii by rabindranath tagore
Song vii by rabindranath tagore 6/1996. (vii. 16.) müm rendelet
6/1996. (vii. 16.) müm rendelet Article xi of the code of ethics for professional teacher
Article xi of the code of ethics for professional teacher 10/2015 (vii. 30) hm
10/2015 (vii. 30) hm Fernando vii absolutismo
Fernando vii absolutismo Ecuacion indicial
Ecuacion indicial Relatii trofice in ecosisteme
Relatii trofice in ecosisteme Keputusan menteri kesehatan ri nomor 829/menkes/sk/vii/1999
Keputusan menteri kesehatan ri nomor 829/menkes/sk/vii/1999 Hikayat hang tuah bab 3
Hikayat hang tuah bab 3 Rima vii becquer comentario
Rima vii becquer comentario Pearson vii
Pearson vii Canto vii inferno
Canto vii inferno Soarele de dupa vii isi arata fata
Soarele de dupa vii isi arata fata Vii meaning
Vii meaning Te har
Te har Rima vii
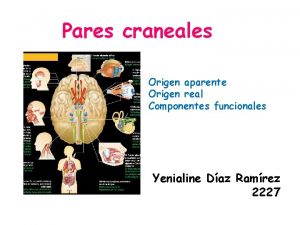
Rima vii Origen aparente del nervio trigemino
Origen aparente del nervio trigemino Title vii of the civil rights act
Title vii of the civil rights act Cranial vii
Cranial vii Title vii of the civil rights act
Title vii of the civil rights act Nerf facial
Nerf facial Sulcus bulbopontinus nedir
Sulcus bulbopontinus nedir Spotkanie w canossie
Spotkanie w canossie Cq bw contest
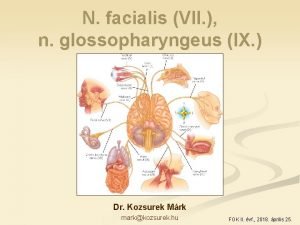
Cq bw contest N.facialis
N.facialis F cl br
F cl br Vii. a skupina
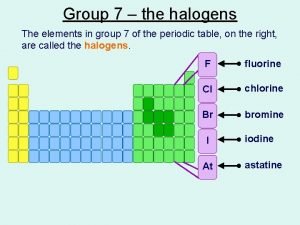
Vii. a skupina Group 7 halogens
Group 7 halogens Vii s
Vii s Vii informe foessa
Vii informe foessa Odpalanie palnika acetylenowo-tlenowego
Odpalanie palnika acetylenowo-tlenowego Hamlet act iv scene iii
Hamlet act iv scene iii Canto 7 paradiso parafrasi
Canto 7 paradiso parafrasi