Regionlis elemzsek mdszerei dr Jeney Lszl egyetemi adjunktus

Regionális elemzések módszerei dr. Jeney László egyetemi adjunktus jeney@elte. hu Regionális elemzések módszerei II. Gazdasági és vidékfejlesztési agrármérnök alapszak (BSc) 2016/2017, I. félév BCE Gazdaságföldrajz és Jövőkutatás Tanszék

Regionális elemzések módszerei n Tematika: területi statisztikai elemzési módszerek Excelben – Adatbázis kezelés, területi egyenlőtlenségi mutatók, földrajzi összefüggés elemzések n Számonkérés: – Félévvégi zh (100 %) – vizsgaidőszakban – Zárthelyi dolgozat tartalma: n Számítógépes gyakorlati feladatok a tanult elemzési módszerek segítségével

Felhasználható irodalom n n n A felkészüléshez elsősorban a gyakorló feladatsor és a Power. Point anyag ajánlott Gyakorló feladatsor letölthető lesz: http: //jeney. web. elte. hu Nemes Nagy, J. (szerk. ) 2005: Regionális elemzési módszerek. – Regionális Tudományi Tanulmányok, 11. – Budapest: ELTE Regionális Földrajzi Tanszék – MTA– ELTE Regionális Tudományi Kutatócsoport, 284 p. Letölthető: http: //geogr. elte. hu/old/REF/Kiadva nyok/REF_11_PDF/RTT-11 tartalom. htm#RTT-11

A regionális elemzések információs forrásai, adatbázisai

Adattípusok

Statisztikai fogalmak n Sokaság: n Ismérvek: n Területi elemzések: legalább 2 ismérv n Adatok jól csoportosíthatók az összehasonlíthatóságuk szerint mérési (vagy adat) skálák rendszere – A megismerni kívánt, megfigyelt egységek halmaza – A sokaság jellemzésére, részekre bontására alkalmas vizsgálati szempontok – Területi ismérv – Változók: időbeli, mennyiségi, minőségi ismérvek

Adatsorok 2 fő típusa: nem fajlagos és fajlagos mutatók n Nem fajlagos (abszolút) mutatók n Fajlagos mutatók (relatív vagy származtatott mutatók) – Pl. népességszám, GDP, személygépkocsik száma, terület, városlakók száma – Jelölése: xi azaz x abszolút mutató értéke adott „i” régióban – Pl. egy főre jutó GDP, ezer lakosra jutó személygépkocsik, népsűrűség, városlakók aránya – Lehet százalékos részesedés is: pl. városlakók aránya – Jelölése: yi azaz y fajlagos mutató értéke adott „i” régióban – Általában 2 nem fajlagos mutató hányadosa, pl. GDP és népesség (ritkán 2 fajlagos mutató hányadosa, pl. megyei GDP/fő az országos átlagos GDP/fő %-ában) – Esetükben súlyozni kell (pl. súlyozott átlag, súlyozott szórás) – A súly a fajlagos mutató képletének nevezőjében van, jelölése fi azaz f súly értéke adott „i” régióban – Súly gyakran népességszám, de nem mindig

Nem fajlagos – fajlagos mutatók valamint a súly közötti átszámítások n Ha a nem fajlagos mutató (GDP) és a súly (népességszám) ismert – A fajlagos mutató (GDP/fő): a nem fajlagos mutató és a súly hányadosa n Ha a nem fajlagos (GDP) és a fajlagos mutató ismert (GDP/fő) – A súly (népesség): a nem fajlagos és a fajlagos mutató hányadosa n Ha a fajlagos mutató (GDP/fő) és a súly (népesség) ismert – Nem fajlagos mutató (GDP): a fajlagos mutató és a súly szorzata

Adatsorok jellegadó értékei

Adatsorok jellegadó értékei n Középértékek – Számtani átlag / súlyozott számtani átlag – Mértani átlag – Helyzeti középértékek (módusz, medián) n Szélső értékek – Maximum – Minimum n Adatsor terjedelme és szórása (átvezet a területi egyenlőtlenségi mutatók felé) – Terjedelem-típusú mutatók – Szórás-típusú mutatók

Középértékek: átlagok n Számtani átlag – Az eredeti számok helyébe helyettesítve azok összege változatlan – n db adat (xi) – Excel fx= ÁTLAG() n Súlyozott számtani átlag – n db fajlagos adat (yi) – Súly (fi): a fajlagos mutató nevezőjében szereplő adat n Mértani átlag – Az eredeti számok helyébe helyettesítve azok szorzata változatlan – n db adat (xi)

Helyzeti középértékek n Medián – Az az érték, aminél kisebb és nagyobb adatok száma egyenlő (felező pont) – Extrém adatokat tartalmazó adatsorok esetében érdemes használni – Kvantilisek: kvartilis (negyedelő), kvintilis (ötödölő), decilis (tizedelő), percentilis (századoló) – Medián/átlag: egyenlőtlenségi mutató (minél kisebb, annál nagyobb az egyenlőtlenség) – Excel fx= MEDIÁN() n Módusz („divatos érték”) – A legtöbbször előforduló érték – Lehet többmóduszú (többcsúcsú) adatsor is – Excel fx= MÓDUSZ()

A szélső értékek és a terjedelem típusú egyenlőtlenségi mutatók n Maximum – Az adatsor legnagyobb értéke (xmax) – Excel fx= MAX() n Minimum – Az adatsor legkisebb értéke (xmin) – Excel fx= MIN() n Alapja a terjedelem típusú egyenlőtlenségi mutatóknak – Range (szóródás terjedelme) – Range-arány (adatsor terjedelme) – Relatív range

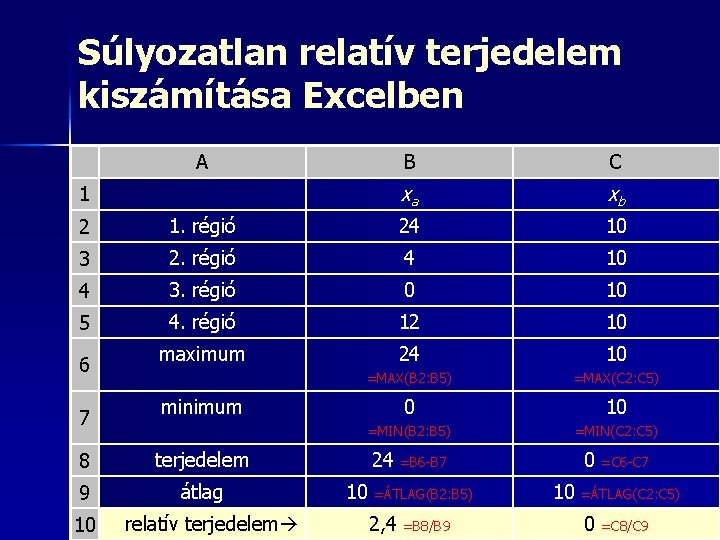
Súlyozatlan relatív terjedelem kiszámításának lépései (abszolút mutatóknál) 1. 2. 3. 4. 5. Ki kell számítani az adatsor maximumát (függvényvarázsló: max) Ki kell számítani az adatsor minimumát (függvényvarázsló: min) Ki kell vonni a maximális értékből a minimálist (ez a terjedelem) Ki kell számítani az adatsor (sima) átlagát (függvényvarázsló: átlag) El kell osztani a terjedelmet az átlaggal

Súlyozatlan relatív terjedelem kiszámítása Excelben A 1 B C xa xb 2 1. régió 24 10 3 2. régió 4 10 4 3. régió 0 10 5 4. régió 12 10 maximum 24 10 =MAX(B 2: B 5) =MAX(C 2: C 5) 0 10 =MIN(B 2: B 5) =MIN(C 2: C 5) 6 7 minimum 8 terjedelem 9 átlag 10 relatív terjedelem 24 10 =ÁTLAG(B 2: B 5) 2, 4 0 =B 6 -B 7 =B 8/B 9 10 =C 6 -C 7 =ÁTLAG(C 2: C 5) 0 =C 8/C 9

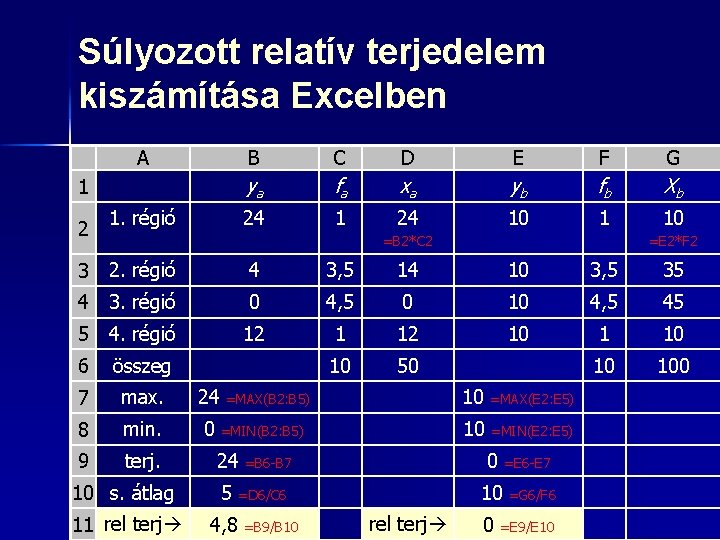
Súlyozott relatív terjedelem kiszámításának lépései (fajlagos mutatóknál) 1. 2. 3. 4. 5. Ki kell számítani az adatsor maximumát (függvényvarázsló: max) Ki kell számítani az adatsor minimumát (függvényvarázsló: min) Ki kell vonni a maximális értékből a minimálist (ez a terjedelem) Ki kell számítani az adatsor súlyozott átlagát El kell osztani a terjedelmet a súlyozott átlaggal

Súlyozott relatív terjedelem kiszámítása Excelben A 1 2 1. régió B C D E F G ya fa xa yb fb Xb 24 10 1 10 =B 2*C 2 =E 2*F 2 3 2. régió 4 3, 5 14 10 3, 5 35 4 3. régió 0 4, 5 0 10 4, 5 45 5 4. régió 12 10 1 10 6 összeg 10 50 10 100 7 max. 24 8 min. 0 9 terj. =MAX(B 2: B 5) =MIN(B 2: B 5) 24 10 s. átlag 5 11 rel terj 4, 8 =MAX(E 2: E 5) 10 =MIN(E 2: E 5) 0 =B 6 -B 7 =E 6 -E 7 10 =D 6/C 6 =B 9/B 10 10 rel terj 0 =G 6/F 6 =E 9/E 10

A szórás típusú egyenlőtlenségi mutatók

Szórás-típusú egyenlőtlenségi mutatók n n n Nem fajlagos (abszolút) mutatók (xi): (súlyozatlan) szórás Fajlagos mutatók (yi): súlyozott szórás A valódi egyenlőtlenségeket a relatív szórással mérhetjük – Nem fajlagos: (súlyozatlan) relatív szórás (szórás az átlag %ában) – Fajlagos mutatók: súlyozott relatív szórás (súlyozott szórás a súlyozott átlag %-ában)

(Súlyozatlan) szórás: nem fajlagos mutatók esetében n n Adatsorok egyes értékeinek (xi) az átlagtól való négyzetes eltérésének az átlaga Képlete – Xi = abszolút mutató i régióban – n = elemszám n Kiszámítása – Excel: fx= SZÓRÁSP() ( és nem SZÓRÁS) – Angol nyelvű Excel fx= STDEVP() n Értékkészlete: 0 ≤ σ ≤ ∞ – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség n Mértékegysége: mint az eredeti értékek (Xi) mértékegysége

(Súlyozatlan) relatív szórás: nem fajlagos mutatók esetében n A valódi egyenlőtlenségeket a relatív szórással mérhetjük Relatív szórás: abszolút mutatók esetében Képlete: – σ = Xi adatsor szórása – x = Xi adatsor átlaga n Kiszámítása – a szórás értékeket elosztjuk az átlaggal és megszorozzuk 100 -zal (a szórás értékeit az átlag százalékában fejezzük ki) n Értékkészlete: 0 ≤ v ≤ ∞ – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség n Mértékegysége: %

Súlyozott szórás: fajlagos mutatók esetében n Fajlagos mutatók (yi) esetében Adatsorok egyes értékeinek (yi) az átlagtól való négyzetes eltérésének az átlaga Képlete – yi = fajlagos mutató i régióban – fi = súly (fajlagos mutató nevezője) n Értékkészlete: 0 ≤ σ ≤ ∞ – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség n Mértékegysége: mint az eredeti értékek (yi) mértékegysége

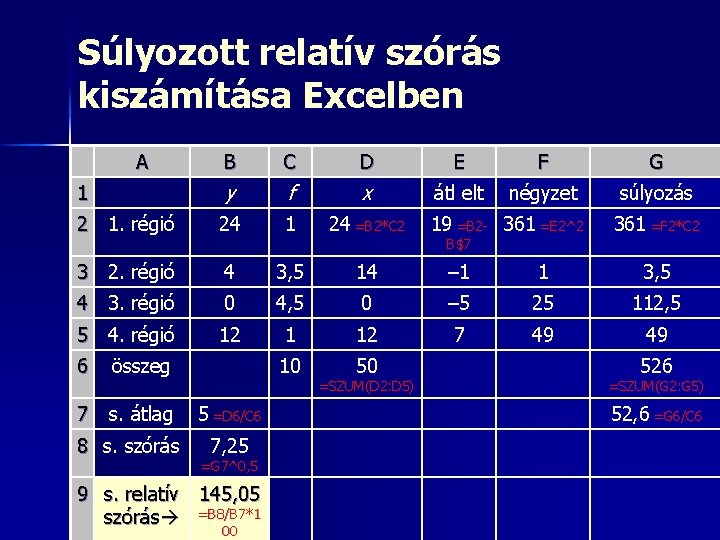
Súlyozott szórás kiszámításának lépései 1. 2. 3. 4. Kiszámítom a fajlagos mutató súlyozott átlagát Minden térség esetében kiszámítom a vizsgált fajlagos mutató értékeinek eltérését a súlyozott átlagtól (Excel $) Minden térség esetében a kapott különbségeket négyzetre emelem (Excel jobb oldali Alt+3 együtt, majd 2 = ^2) Minden térség esetében a kapott értékeket megszorzom a térséghez tartozó súllyal – 2– 4. lépések egy oszlopban is megoldhatók 5. 6. 7. Az így kapott szorzatokat összegzem Ezt az összeget elosztom a súlyok összegével Ennek a hányadosnak a négyzetgyökét veszem (^0, 5)

Súlyozott relatív szórás: fajlagos mutatók esetében n A valódi egyenlőtlenségeket a relatív szórással mérhetjük – Fajlagos mutatók esetében: súlyozott relatív szórással n Képlete: – σ = yi adatsor súlyozott szórása – y = yi adatsor súlyozott átlaga n Kiszámítása – A súlyozott szórás értékeket elosztjuk a súlyozott átlaggal és megszorozzuk 100 -zal (a súlyozott szórás értékeit a súlyozott átlag százalékában fejezzük ki) n Értékkészlete: 0 ≤ v ≤ ∞ – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség n Mértékegysége: %

Súlyozott relatív szórás kiszámítása Excelben A B C D E F G 1 y f x átl elt négyzet súlyozás 2 1. régió 24 1 24 =B 2*C 2 19 =B 2 - 361 =E 2^2 361 =F 2*C 2 3 2. régió 4 3, 5 14 – 1 1 3, 5 4 3. régió 0 4, 5 0 – 5 25 112, 5 5 4. régió 12 1 12 7 49 49 10 50 6 összeg 7 s. átlag 8 s. szórás 5 =D 6/C 6 7, 25 =G 7^0, 5 9 s. relatív 145, 05 szórás =B 8/B 7*1 00 =SZUM(D 2: D 5) B$7 526 =SZUM(G 2: G 5) 52, 6 =G 6/C 6

A területi koncentráció mérése: Hirschman–Herfindahl index

Területi egyenlőtlenségek mérésére szolgáló statisztikai eszközök n Területi egyenlőtlenségi indexek, leggyakrabban használtak: – A területi polarizáltság mérőszámai n n Relatív terjedelem/Relatív range (Q) Duál mutató/Éltető–Frigyes index (D) – Szórás-típusú területi egyenlőtlenségi indexek n Súlyozott relatív szórás (V) – Területi eloszlást mérő egyenlőtlenségi indexek n n Hirschman–Herfindahl index (K) Hoover-index/Krugman-index (H) – Területi egyenlőtlenségek összetettebb mérési módszerei n n n Gini együttható (G) Távolságfüggvények Korrelációs mérőszámok

Hirschman–Herfindahl index n n n Egy jelenség földrajzi koncentrációjának mérésére használt mutatószám Csak összegezhető (nem fajlagos) mutatóra számítható Képlete – Xi = nem fajlagos mutató i régióban – Σxi = nem fajlagos mutató a teljes régióban n Értékkészlete: 1/n ≤ K ≤ 1 – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség – Előfordulhat, hogy alacsonyabb területi szinten csökken az értéke n Mértékegysége: nincs

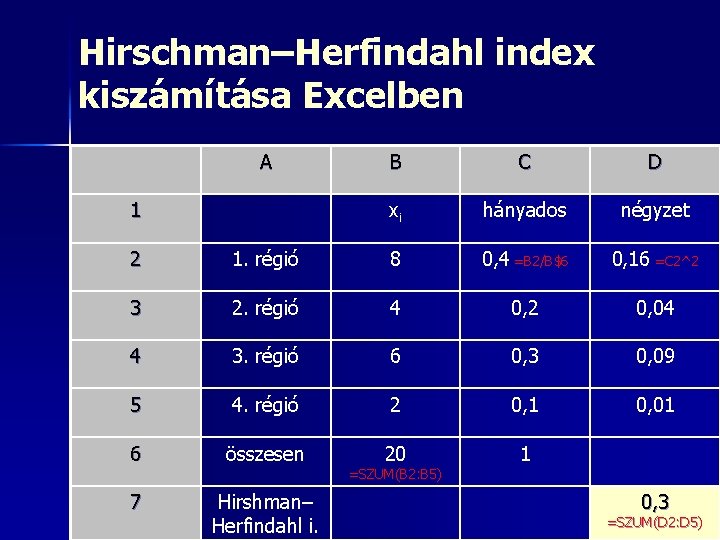
Hirschman–Herfindahl index kiszámításának lépései 1. 2. 3. Összegezzük a vizsgált adatsort Minden térség esetében elosztom az adott térség értékét az előbb kiszámított összeggel (Excel $) Minden térség esetében a kapott hányadosokat négyzetre emelem (Excel jobb oldali Alt+3 együtt, majd 2 = ^2) – 2– 3. lépések egy oszlopban is megoldhatók 4. Az így kapott értékeket összegzem

Hirschman–Herfindahl index kiszámítása Excelben A 1 B C D xi hányados négyzet 2 1. régió 8 0, 4 =B 2/B$6 0, 16 =C 2^2 3 2. régió 4 0, 2 0, 04 4 3. régió 6 0, 3 0, 09 5 4. régió 2 0, 1 0, 01 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 0, 3 =SZUM(D 2: D 5)

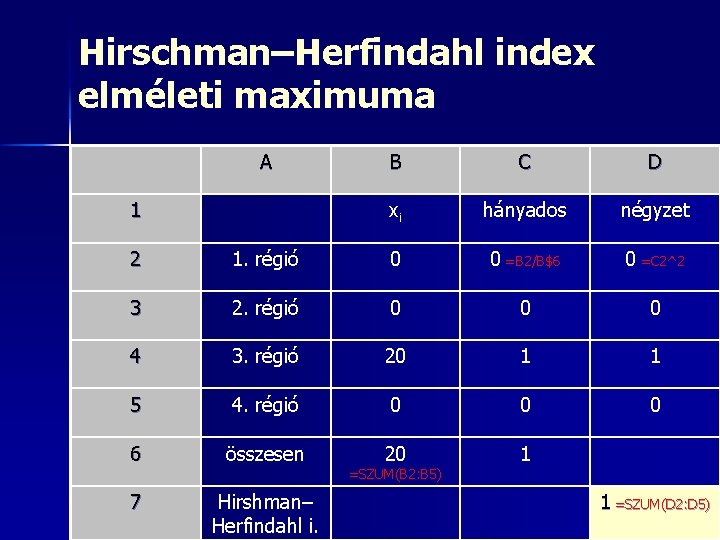
Hirschman–Herfindahl index elméleti maximuma A 1 B C D xi hányados négyzet 2 1. régió 0 0 =B 2/B$6 0 =C 2^2 3 2. régió 0 0 0 4 3. régió 20 1 1 5 4. régió 0 0 0 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 1 =SZUM(D 2: D 5)

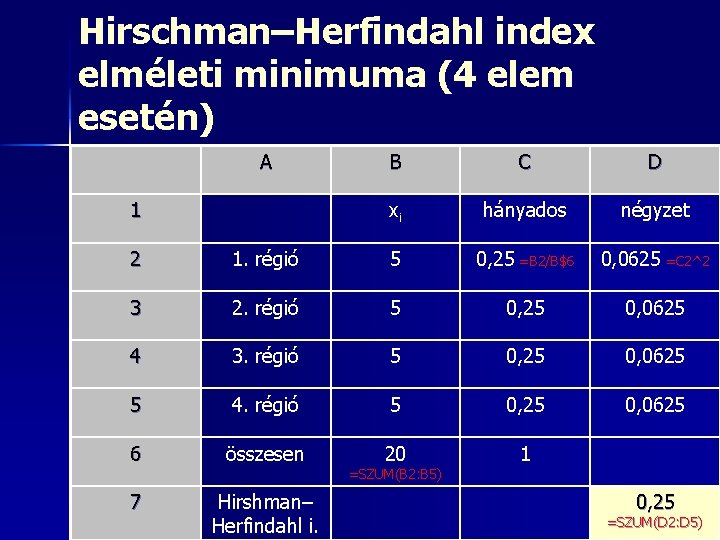
Hirschman–Herfindahl index elméleti minimuma (4 elem esetén) A 1 B C D xi hányados négyzet 2 1. régió 5 0, 25 =B 2/B$6 0, 0625 =C 2^2 3 2. régió 5 0, 25 0, 0625 4 3. régió 5 0, 25 0, 0625 5 4. régió 5 0, 25 0, 0625 6 összesen 20 1 7 Hirshman– Herfindahl i. =SZUM(B 2: B 5) 0, 25 =SZUM(D 2: D 5)

Területi eloszlások összevetése: Hoover index

Hoover index n n Egyik legelterjedtebb, legáltalánosabban használt területi egyenlőtlenségi index Két mennyiségi ismérv területi megoszlásának eltérését méri – Az egyik ismérv, társadalmi-gazdasági jelenség mennyiségének hány százalékát kell a területi egységek között átcsoportosítani ahhoz, hogy területi megoszlása a másik jellemzőével azonos legyen – Területi kutatásokban leggyakrabban a népesség területi eloszlásával vetjük össze más társadalmi-gazdasági ismérvével n n 1941: E. M. Hoover, amerikai agrárközgazdász Használja a földrajz, szociológia, közgazdaságtan, ökológia is

Hoover index n Két nem fajlagos mutató területi megoszlása közötti eltérést mérhetjük vele – Egy fajlagos mutató számlálója és nevezője között is lehet n Képlete: n xi és yi: két megoszlási viszonyszám, melyekre fennállnak – xi = i régió részesedése x nem fajlagos mutatóból – yi = i régió részesedése y nem fajlagos mutatóból az alábbi összefüggések – Σxi = 100 – Σyi = 100 n A mutató szimmetrikus, a két összevetett megoszlás (xi és yi) szerepe, sorrendje felcserélhető Értékkészlete: 0 ≤ H ≤ 100 n Mértékegysége: % n – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség

Hoover index kiszámításának lépései 1. 2. 3. 4. Mindkét nem fajlagos mutató adatsorának értékeit összegezzük Minden térség esetében kiszámítjuk az adott térség százalékos részesedését az összes mennyiségből (mindkét mutató esetében) Minden térség esetében kivonjuk az egyik mutató szerinti százalékos részesedésből a másik mutató szerinti százalékos részesedést Minden térség esetében az így kapott különbségek abszolút értékét vesszük (ABS) – 2– 4. lépések egy oszlopban is megoldhatók 5. 6. Az abszolút értékeket összegzem A kapott összeg értékét megfelezem

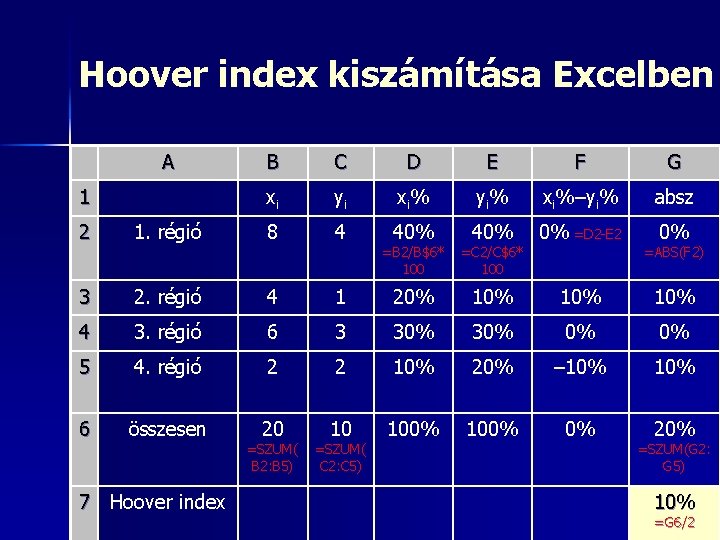
Hoover index kiszámítása Excelben A 1 B C D E F G xi yi xi% yi% xi%–yi% absz 40% =B 2/B$6* 100 40% =C 2/C$6* 100 0% =D 2 -E 2 0% 2 1. régió 8 4 3 2. régió 4 1 20% 10% 10% 4 3. régió 6 3 30% 0% 0% 5 4. régió 2 2 10% 20% – 10% 6 összesen 20 10 100% 0% 20% 7 Hoover index =SZUM( B 2: B 5) =SZUM( C 2: C 5) =ABS(F 2) =SZUM(G 2: G 5) 10% =G 6/2

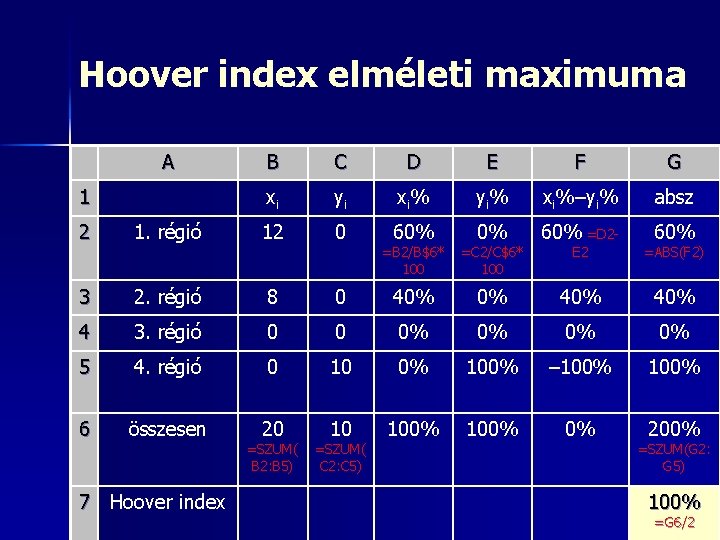
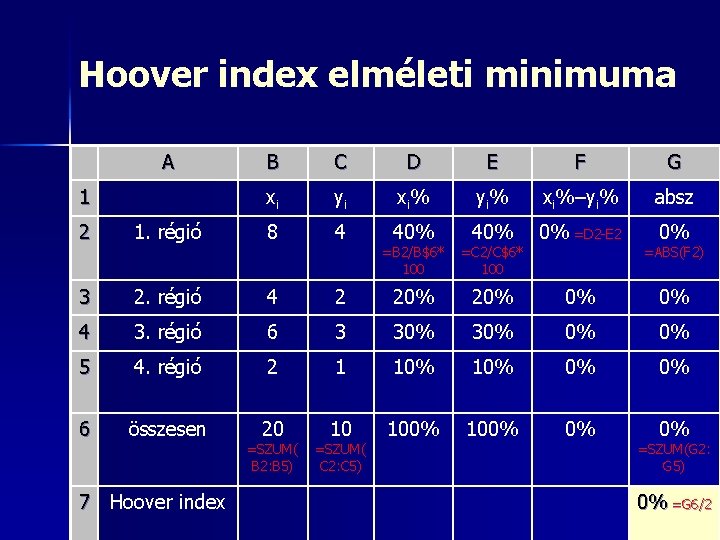
Hoover index elméleti maximuma A 1 B C D E F G xi yi xi% yi% xi%–yi% absz 60% =B 2/B$6* 100 0% =C 2/C$6* 100 60% =D 2 E 2 60% =ABS(F 2) 2 1. régió 12 0 3 2. régió 8 0 40% 0% 40% 4 3. régió 0 0 0% 0% 5 4. régió 0 10 0% 100% – 100% 6 összesen 20 10 100% 0% 200% 7 Hoover index =SZUM( B 2: B 5) =SZUM( C 2: C 5) =SZUM(G 2: G 5) 100% =G 6/2

Hoover index elméleti minimuma A 1 B C D E F G xi yi xi% yi% xi%–yi% absz 40% =B 2/B$6* 100 40% =C 2/C$6* 100 0% =D 2 -E 2 0% 2 1. régió 8 4 3 2. régió 4 2 20% 0% 0% 4 3. régió 6 3 30% 0% 0% 5 4. régió 2 1 10% 0% 0% 6 összesen 20 10 100% 0% 0% 7 Hoover index =SZUM( B 2: B 5) =SZUM( C 2: C 5) =ABS(F 2) =SZUM(G 2: G 5) 0% =G 6/2

„Pszeudo-egymutatós” egyenlőtlenségi index n Két nem fajlagos mutató területi eloszlása közötti eltérés mérése – Pl. nép-jöv, kisebbség-egész társadalom stb. n Egy fajlagos mutató területi egyenlőtlenségének mérése – Pl. Jöv/fő, kisebbségek aránya

Hoover index használhatósága n Egyik legjobban interpretálható eredményt adja a területi egyenlőtlenségi indexek közül – Értékei 0– 100 között mozognak: a 100 magas, a 0 alacsony érték (szórás-típusú területi egyenlőtlenségi mutatóknak nincs maximuma) – H = 33% az egyik mutató 33 %-át kell a régiók között átcsoportosítani ahhoz, hogy a területi megoszlása megegyezzen a másikéval

Hoover index más neveken n Robin Hood index („Rózsa Sándor” index) n Dinamikus értelmezés (itt lehet az egy évre jutó változást is mérni, ha 2 helyett 2 t-vel osztunk) – Népesség és jövedelem között – Korábbi és későbbi állapotok között n (Településszociológiában Duncan&Duncan házaspár) n Egyes változatoknál nem százalékban fejezzük ki, ekkor értékkészlete: 0 ≤ H ≤ 1 Krugman index (Földrajz és kereskedelem c. könyv, 1993. ) n – Disszimilaritási index: rész–rész viszonylatban – Szegregációs index: rész–egész viszonylatban, vagy rész–többi rész viszonylatban – Ha nem osztjuk el 2 -vel (nehezebben értelmezhető) – 0 ≤ H ≤ 200 (vagy 0 ≤ H ≤ 2)

Hoover index vizsgálati lehetőségei n n Magyarország 2005 jöv-nép megyei szint Egy számítás önmagában általában kevés összehasonlítás kell: – – – Területek között: pl. Szlovákiára is Időbeni állapotok között: pl. 1990 -re is Mutatók között: pl. személygépkocsi és a népesség között is – Területi szinteken (Hoover-index specialitása): pl. települési szinten is

Különböző területi szintek egyenlőtlenségek eltérő alakulása n Az adóköteles jövedelmek területi egyenlőtlenségeinek változása különböző területi szinteken, Robin Hood index, 1998 – 2002

Területi egyenlőtlenségek összetettebb mérési módszere: Gini együttható

Gini együttható n Elnevezés: Corrado Gini – Olasz statisztikus, demográfus, társadalomkutató, közgazdász n n n 1912. : Variabilità e mutabilità Általában a jövedelem és a jólét egyenlőtlenségének mérésére használják Használja az egészségügy, ökológia, vegyészet is

Súlyozatlan Gini együttható n n Csak abszolút mutatóra számítható Képlete – – – n n n xi = abszolút mutató i régióban xj = abszolút mutató j régióban n = elemszám (régiók száma) Értékkészlete: 0 ≤ G ≤ 1– 1/n Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség Mértékegysége: nincs (dimenziótlan)

Súlyozatlan Gini együttható kiszámításának lépései 1. Mátrix készítése: felső és (bal) oldalsó keretében a vizsgált abszolút mutató – Fejléc: másolás irányított beillesztés transzponálás értéket 2. Mátrix belsejének kitöltése: fejléc és oldalléc értékeinek egymásból kivonása, különbség abszolút értékbe tétele – $ megfelelő használata: fejlécnél sorazonosító szám elé, oldallécnél oszlopazonosító betű elé) – Ha jó mátrix átlójában 0 értékek szerepelnek 3. 4. 5. Mátrix összes elemének összegzése Abszolút adatsor átlagának kiszámítása (függvényvarázsló - átlag) Mátrix összegének elosztása a vizsgált adatsor ("sima") átlagával, az elemszám négyzetével, és 2 -vel

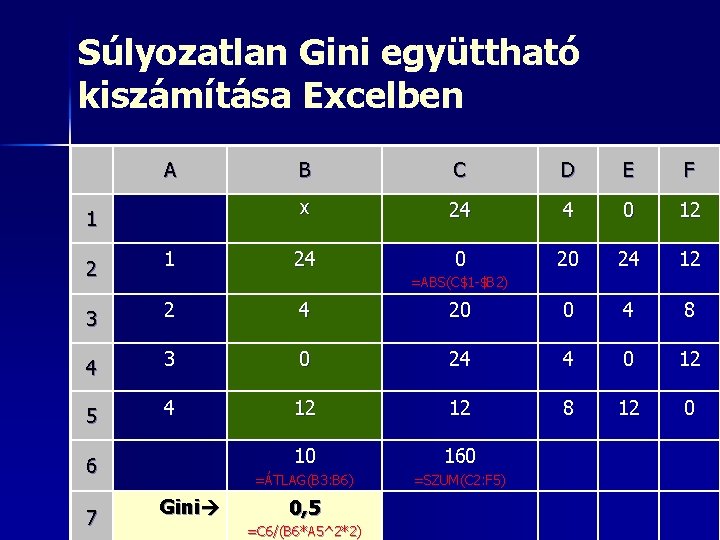
Súlyozatlan Gini együttható kiszámítása Excelben A 1 2 1 B C D E F x 24 4 0 12 24 0 20 24 12 =ABS(C$1 -$B 2) 3 2 4 20 0 4 8 4 3 0 24 4 0 12 5 4 12 12 8 12 0 10 160 =ÁTLAG(B 3: B 6) =SZUM(C 2: F 5) 6 7 Gini 0, 5 =C 6/(B 6*A 5^2*2)

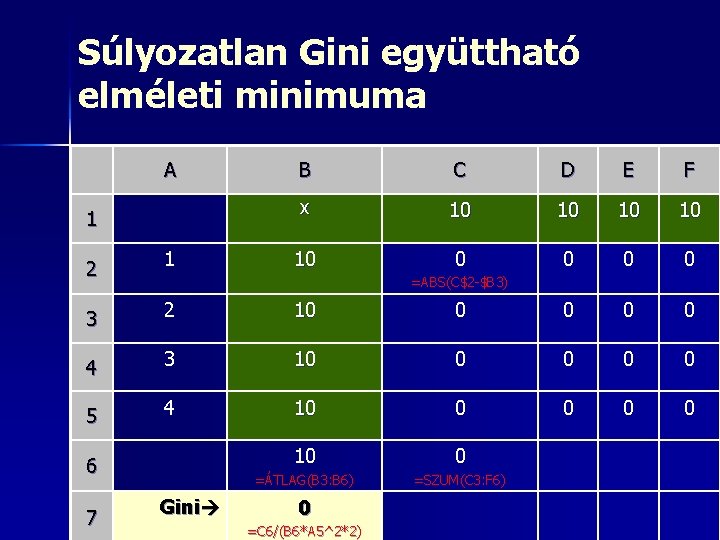
Súlyozatlan Gini együttható elméleti minimuma A 1 2 1 B C D E F x 10 10 10 0 0 =ABS(C$2 -$B 3) 3 2 10 0 0 4 3 10 0 0 5 4 10 0 0 10 0 =ÁTLAG(B 3: B 6) =SZUM(C 3: F 6) 6 7 Gini 0 =C 6/(B 6*A 5^2*2)

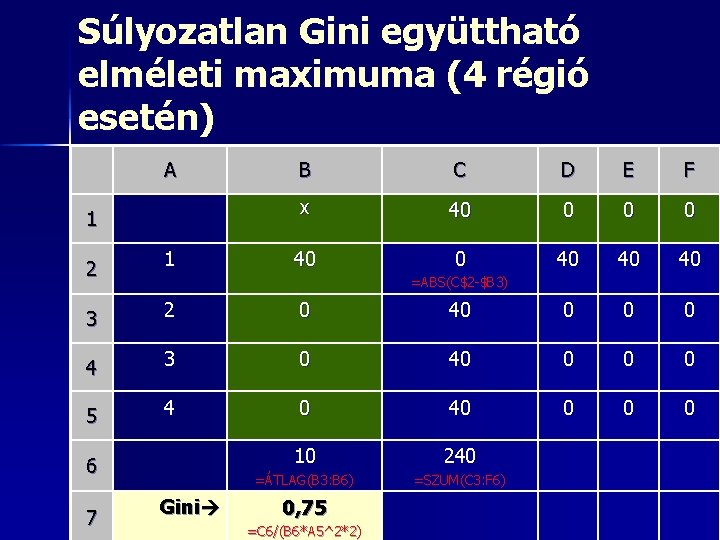
Súlyozatlan Gini együttható elméleti maximuma (4 régió esetén) A 1 2 1 B C D E F x 40 0 40 40 40 =ABS(C$2 -$B 3) 3 2 0 40 0 4 3 0 40 0 5 4 0 40 0 10 240 =ÁTLAG(B 3: B 6) =SZUM(C 3: F 6) 6 7 Gini 0, 75 =C 6/(B 6*A 5^2*2)

Súlyozott Gini együttható n n Csak fajlagos mutatóra számítható Képlete – – n yi = fajlagos mutató i régióban yj = fajlagos mutató j régióban fi = súly i régióban fj = súly j régióban Értékkészlete: 0 ≤ Gs ≤ 1–Σf/fymax – Minél nagyobb az értéke, annál nagyobb az egyenlőtlenség n Mértékegysége: nincs (dimenziótlan)

Súlyozott Gini együttható kiszámításának lépései 1. Mátrix készítése: 2 felső és 2 (bal) oldalsó keretében a vizsgált fajlagos mutató és a hozzátartozó súly – Fejléc: másolás irányított beillesztés transzponálás értéket 2. Mátrix belsejének kitöltése: fejléc és oldalléc fajlagos értékeinek egymásból kivonása, különbség abszolút értékbe tétele, majd ennek megszorozása a fejlécben és az oldallécben szereplő súlyokkal – $ megfelelő használata: fejlécnél sorazonosító szám elé, oldallécnél oszlopazonosító betű elé) – Ha jó mátrix átlójában 0 értékek szerepelnek 3. 4. 5. Mátrix összes elemének összegzése Fajlagos adatsor súlyozott átlagának kiszámítása Mátrix összegének elosztása a vizsgált adatsor súlyozott átlagával, a súlyok összegének négyzetével, és 2 -vel

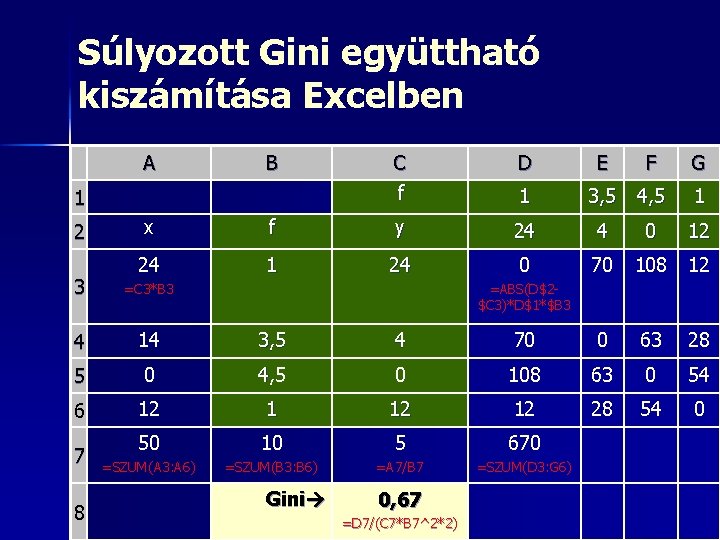
Súlyozott Gini együttható kiszámítása Excelben A B 1 2 C f D 1 E F 3, 5 4, 5 G 1 x f y 24 4 0 12 24 1 24 0 70 108 12 3 =C 3*B 3 4 14 3, 5 4 70 0 63 28 5 0 4, 5 0 108 63 0 54 6 12 12 28 54 0 50 10 5 670 =SZUM(A 3: A 6) =SZUM(B 3: B 6) =A 7/B 7 =SZUM(D 3: G 6) 7 8 =ABS(D$2$C 3)*D$1*$B 3 Gini 0, 67 =D 7/(C 7*B 7^2*2)

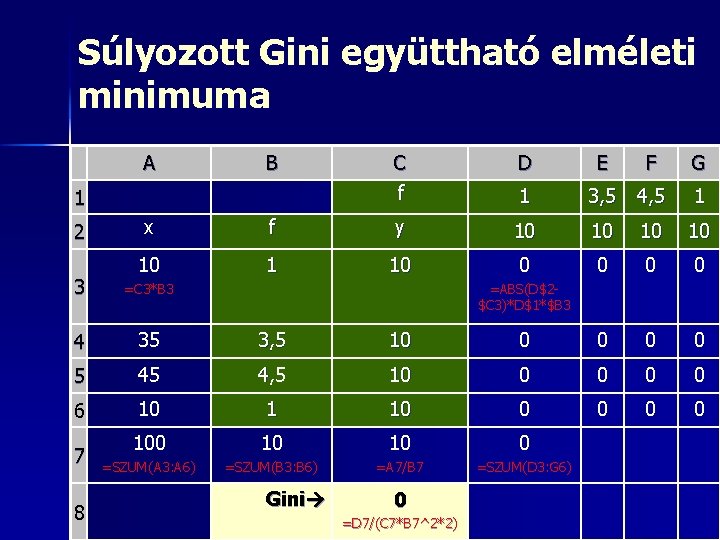
Súlyozott Gini együttható elméleti minimuma A B 1 2 C f D E F G 1 3, 5 4, 5 1 x f y 10 10 10 1 10 0 0 3 =C 3*B 3 4 35 3, 5 10 0 0 5 45 4, 5 10 0 0 6 10 1 10 0 0 10 10 0 =SZUM(A 3: A 6) =SZUM(B 3: B 6) =A 7/B 7 =SZUM(D 3: G 6) 7 8 =ABS(D$2$C 3)*D$1*$B 3 Gini 0 =D 7/(C 7*B 7^2*2)

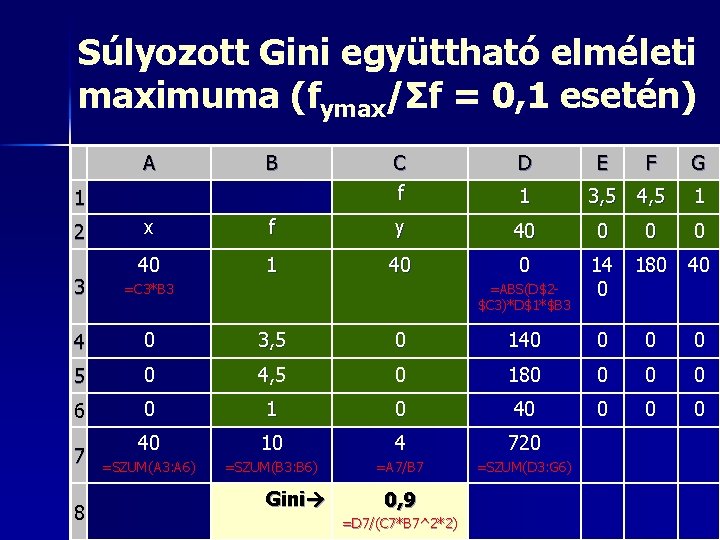
Súlyozott Gini együttható elméleti maximuma (fymax/Σf = 0, 1 esetén) A B 1 2 C f D 1 E F 3, 5 4, 5 G 1 x f y 40 0 40 1 40 0 14 0 180 40 3 =C 3*B 3 4 0 3, 5 0 140 0 5 0 4, 5 0 180 0 6 0 1 0 40 10 4 720 =SZUM(A 3: A 6) =SZUM(B 3: B 6) =A 7/B 7 =SZUM(D 3: G 6) 7 8 =ABS(D$2$C 3)*D$1*$B 3 Gini 0, 9 =D 7/(C 7*B 7^2*2)

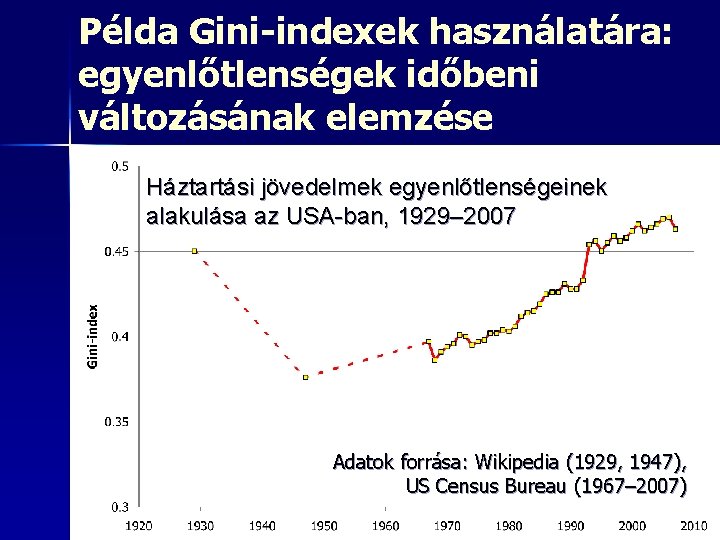
Példa Gini-indexek használatára: egyenlőtlenségek időbeni változásának elemzése Háztartási jövedelmek egyenlőtlenségeinek alakulása az USA-ban, 1929– 2007 Adatok forrása: Wikipedia (1929, 1947), US Census Bureau (1967– 2007)

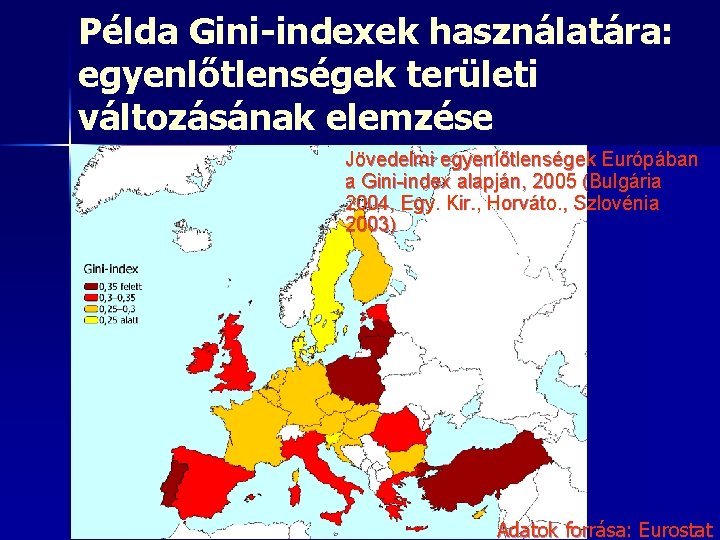
Példa Gini-indexek használatára: egyenlőtlenségek területi változásának elemzése Jövedelmi egyenlőtlenségek Európában a Gini-index alapján, 2005 (Bulgária 2004, Egy. Kir. , Horváto. , Szlovénia 2003) Adatok forrása: Eurostat

Példa Gini-indexek használatára: egyenlőtlensége területi változásának elemzése World Bank (World Development Indicators): 0– 100 között ENSZ (UNDP) is hivatkozik rá – http: //hdrstats. undp. org/en/indicators/ – Namíbia: 74, 3%, Dánia 24, 7% CIA World Factbook: „distribution in family income”: – Namíbia (2003): 70, 7%, Svédország (2005): 23%

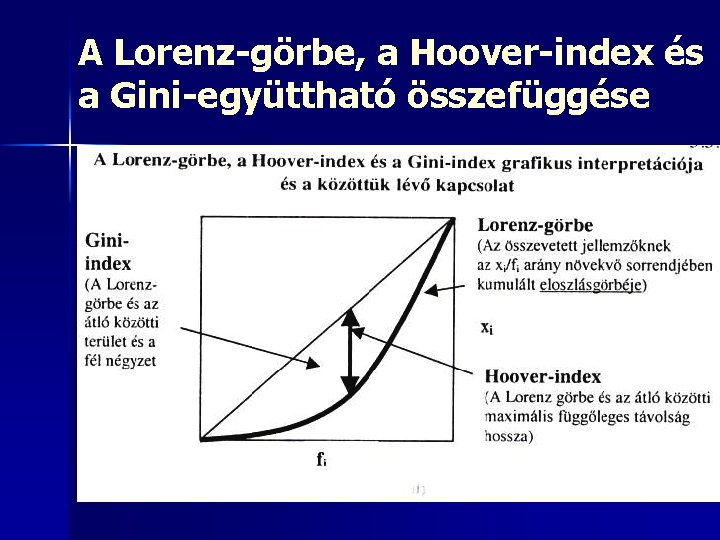
A Lorenz-görbe, a Hoover-index és a Gini-együttható összefüggése

Földrajzi összefüggések elemzése: sztochasztikus módszerek

Társadalmi jelenségek együttmozgása n n Földrajzi összefüggések elemzése: sztochasztikus módszerek Tagoltság vizsgálata: szinte sohasem szűkül le egy-egy jelenség (mutatószám) térbeli eloszlásának elemzésére – Már a fajlagos adatok egyenlőtlenségeinek mérésekor is 2 jelenséget kapcsolunk össze n n Térbeli együttmozgások elemzése: kifejezetten területi kölcsönhatások (néha ok-okozati kapcsolatok) is megjelennek Összefüggések mérése: korreláció- és regressziószámítás – Erősség: milyen erős az összefüggés – Irány: egyenes (+) vagy fordított (–) arányosság

Szignifikancia n n n Megbízható (szignifikáns) összefüggés: ha viszonylag nagy elemszámú mintából, hosszú adatsorból számítjuk Erős szignifikancia: megfigyelési egységek körét véletlenszerűen újabbakkal bővítve, nagy valószínűséggel nem változik az összefüggés iránya és szorossága Meghatározza: – – n Elemszámtól (1000 vagy 10 területi egységre mérünk) Kapcsolat szorossági szintje (korreláció absz. 0, 9 vagy 0) Szignifikancia-tesztek: pl. SPSS

Korreláció

Korreláció n Jelzőszámok közötti kapcsolat szorosságának meghatározására szolgáló eljárás (egyfajta sajátos egyenlőtlenségi mutató – Egy mutatószámmal (r): korrelációs együttható n Korreláció típusai területi elemzésekben – Lineáris korreláció azonos megfigyelési egységekre vonatkozó két adatsor között – Autokorreláció – Keresztkorreláció n n Ugyanígy lehet autoregresszió és keresztregresszió is Értékkészlete: – 1 ≤ r ≤ 1 Mértékegysége nincs Súlyozás problémája a korrelációszámításban

A korrelációs-együtthatók értékeinek értelmezése r értéke r=1 kapcsolat jellege 0, 7 ≤ r < 1 Szoros kapcsolat, egyirányú együttmozgás 0, 3 ≤ r < 0, 7 Közepes erősségű kapcsolat, egyirányú együttmozgás 0 < r < 0, 3 Gyenge kapcsolat, egyirányú együttmozgás r=0 Nincs lineáris kapcsolat, a két jellemző korrelálatlan – 0, 3 < r < 0 Gyenge kapcsolat, ellentétes irányú együttmozgás Lineáris függvénykapcsolat, egyenes arányosság van a két jellemző között – 0, 7 < r ≤ – 0, 3 Közepes erősségű kapcsolat, ellentétes irányú együttmozgás – 1 < r ≤ – 0, 7 Szoros kapcsolat, ellentétes irányú együttmozgás r = – 1 Lineáris függvénykapcsolat, fordított arányosság van a két jellemző között

Lineáris korreláció n Lineáris korreláció azonos megfigyelési egységekre vonatkozó két adatsor között – r = corr (xi yi) n n Legismertebb: Pearson-féle korrelációs együttható Egyfajta sajátos egyenlőtlenségi mutató

Lineáris korrelációs együtthatók n Pearson-féle lineáris korreláció együttható – Excel fx= KORREL() – Angol nyelvű Excel fx= CORREL() n Spearman-féle rangkorreláció – Ordinális (sorrendi) adatskála esetén – di: összetartozó rangszámok különbségei

Korrelációs mátrix n n n f(x) függvényvarázsló segítségével számítható A mátrixban szereplő adatsorok egymás mellé rendezése úgy, hogy üres oszlop és egyéb adat ne legyen benne! Mátrix keretének elkészítése a fejléc átmásolása vízszintesen és függőlegesen, a bal fölső cella üres) Minden sorból egy korrelációs együttható kiszámítása, a sorban állandó jelzőszám tömbjének betűjeli lerögzítendők! (További egyszerűsítés is végezhető, de teljesen automatikusan nem lehet kitölteni minden cellát!) Ellenőrzés: átlóban 1 -esek szerepelnek, a mátrix az átlóra szimmetrikus

Keresztkorreláció n n Két adatsor különböző (időben eltolt vagy térben szomszédos) megfigyelési egységekre vonatkozó értékei közötti kapcsolat Időbeli keresztkorreláció – r = corr (xi yi–k) n Területi keresztkorreláció – r = corr (xi ys(i))

Autokorreláció n n Egyazon adatsor különböző (időben eltolt vagy térben szomszédos) megfigyelési egységekre vonatkozó értékei közötti kapcsolat Időbeni autokorreláció: minden i-edik időponthoz tartozó xi értékhez ugyanezen x változónak egy k évvel eltolt (k évvel korábbi) adatát rendelve számítjuk adatsor hossza k évvel csökken – r = corr (xi xi–k) n Területi autokorreláció: i-edik megfigyelési területegység xi adatához a vele szomszédos területegységek értékeit (átlagát) számítjuk – r = corr (xi xs(i))

Regresszió-elemzés

Regressziószámítás a regionális elemzésekben n n Változókapcsolatokat valószínűségi (sztochasztikus) függvénykapcsolatként értelmezi Függő és független (vagy magyarázó) változók – Független: x tengely, fajlagos mutató nevezője, bal oszlop – Függő: y tengely, fajlagos mutató számlálója, jobb oszlop n Típusai: – Lineáris vagy nem lineáris – Két- vagy többváltozós n Alkalmas becslésre, előrejelzésre

Kétváltozós lineáris regresszió n y = a + bx – x: magyarázó (független) változó – b: regressziós együttható (regressziós koefficiens): az egyenes meredekségét vagy dőlését jelöli (az x értékének egységnyi növekedése y értékének mekkora mértékű és milyen irányú változását vonja maga után – a: regressziós állandó (konstans): értéke megegyezik az egyenes y tengelyen tapasztalt metszéspontjával (a értéke egyenlő y értékével x=0 helyen) – y: a függő változó regressziós egyenlet alapján becsült értéke n Determinációs együttható (R 2) itt a Pearson-féle lineáris korrelációs együttható négyzete

Kétváltozós lineáris regresszó számítása Excelben 1. 2. 3. 4. 5. 6. A két adatsor egymás mellé rendezése úgy, hogy a bal oldalon az x tengelyre kerülő változó legyen. Szórásdiagram készítése (pontdiagram) Formázási műveletek Jobb klikk valamely pontra: trendvonal felvétele Egyenlet és r négyzet látszik Számítás

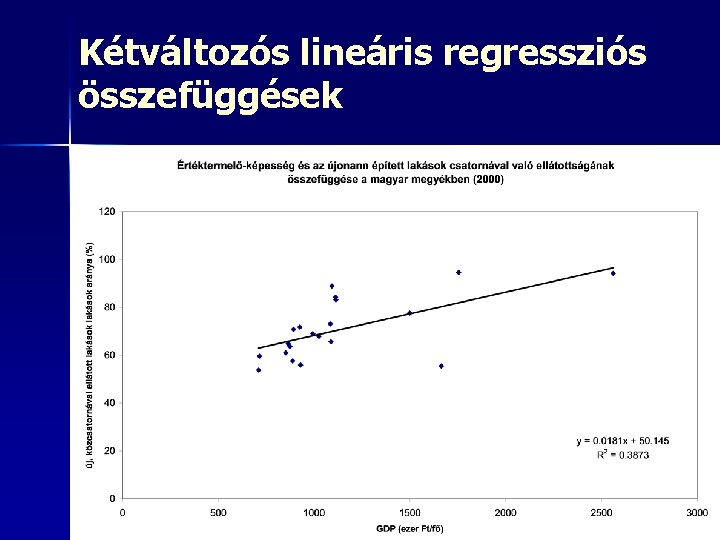
Kétváltozós lineáris regressziós összefüggések

Nem lineáris összefüggések n Nem lineáris regressziós egyenletek alaptípusai n Determináció együttható (R 2)dönti el, melyik írja le legjobban az adott összefüggést – – – Logaritmikus: y = a + (b*lnx) Polinomiális: y = a + (b 1*x) + (b 2*x 2) + … + (bn*xn) Exponenciális y = a*bx Hiperbolikus y =a +b/x Hatványkitevős y = a*xb – Azt a trendvonaltípust érdemes választani, amelynél magasabb az R 2 értéke n n Elemzésük és értelmezésük nehézkesebb, mint a lineáris egyenleteké Idősorok elemzésénél, trendszámításban gyakrabban használják mint a területi adatok keresztmetszeti vizsgálatában

Nem lineáris összefüggések n Nem lineáris regressziós egyenletek alaptípusai – – – n n n Logaritmikus: y = a + (b*lnx) Polinomiális: y = a + (b 1*x) + (b 2*x 2) + … + (bn*xn) Exponenciális y = a*bx Hiperbolikus y =a +b/x Hatványkitevős y = a*xb Determináció együttható dönti el, melyik írja le legjobban az adott öszefüggést Elemzésük és értelmezésük nehézkesebb, mint a lineáris egyenleteké Idősorok elemzésénél, trendszámításban gyakrabban használják mint a területi adatok keresztmetszeti vizsgálatában

Idősorok elemzése

Idősorok elemzése n n n Idősorok típusai: állapot és tartam idősorok Idősorok összetevői: trend, ingadozások, törések Trendelemzés előre- vagy visszajelzés Időbeli mozgóátlag Bázisindex, láncindex Évi átlagos növekedési ráta

Idősorok típusai: állapot és tartam idősorok n Tartam idősorok: – Pl. csapadék, vándorlás, természetes szaporodás, külföldi működő-tőke beáramlása, turista-érkezések – Adatsor tagjai összegezhetők (pl. napi csapadékok � havi csapadék) – Adatsor tagjai csoportosíthatók (pl. minden év januári vendégforgalma) n Állapot idősorok: – Pl. népességszám, GDP, munkanélküliek, személygépkocsik – Adatsor tagjai nem összegezhetők (max átlagolhatók) n Mindkét idősortípusra igaz: – Tagok sorrendje kötött, fel nem cserélhető, időrend (területi adatsor esetén ilyen nincs)

Analitikus trendelemzés n Regresszió segítségével – Független változó: vízszintes (x) tengely t tengely – Függő változó: függőleges y tengely n n Trendvonal mutatja az idősor fő tendenciáját Trendvonallal becsülni is lehet: adott t időpontban mekkora y érték valószínűsíthető a trend alapján – – – n Trendvonal meghosszabbítása előre: előrejelzés (prognózis) Trendvonal meghosszabbítása hátra: visszajelzés a múltra Az idősor ismert időtartalmán belüli, „közbülső” t időpontban becslés y értékére Előre-vagy visszajelzés: annyival lehet előre- vagy visszajelezni, amilyen hosszú ismert idősorunk van

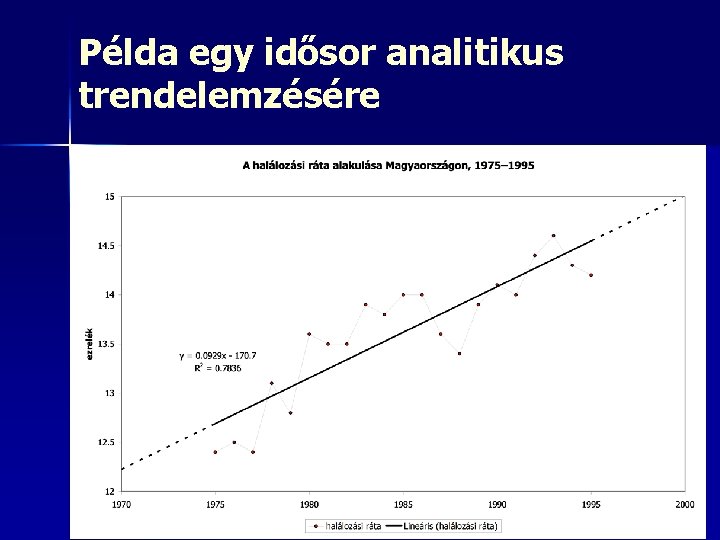
Példa egy idősor analitikus trendelemzésére

Időbeli mozgóátlag n Idősor tagjainak eredeti értéke helyett az idősorban szomszédjaival közös tagjainak átlagértékét vesszük figyelembe – Átlagolásba 3, 5, 7 vagy több tag is bevonható (minél több annál inkább rövidül az adatsor) – A mozgóátlagolás többször is megismételhető: az átlagértékeket is lehet tovább átlagolni (minél többször, annál inkább rövidül az adatsor) n Előnye: – Egyszerűbb matematikai háttér (csak átlagolni kell) n Hátránya: – Rövidül az idősor csak hosszú idősorok esetén érdemes alkalmazni n Nem lehet vele előrejelzést készíteni

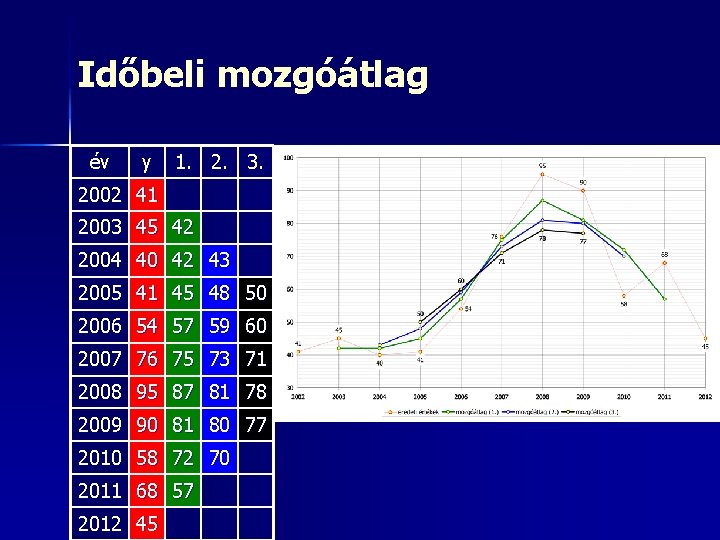
Időbeli mozgóátlag év y 1. 2. 3. 2002 41 2003 45 42 2004 40 42 43 2005 41 45 48 50 2006 54 57 59 60 2007 76 75 73 71 2008 95 87 81 78 2009 90 81 80 77 2010 58 72 70 2011 68 57 2012 45

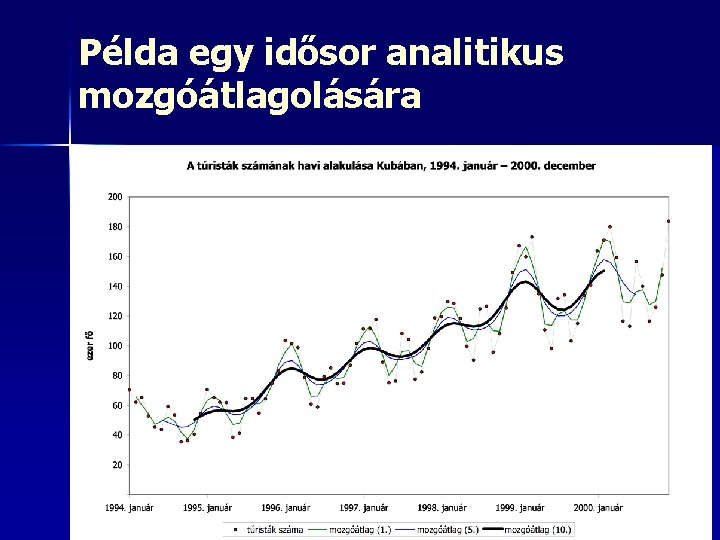
Példa egy idősor analitikus mozgóátlagolására