RazumovStroganov Vincent Pasquier Service de Physique Thorique C






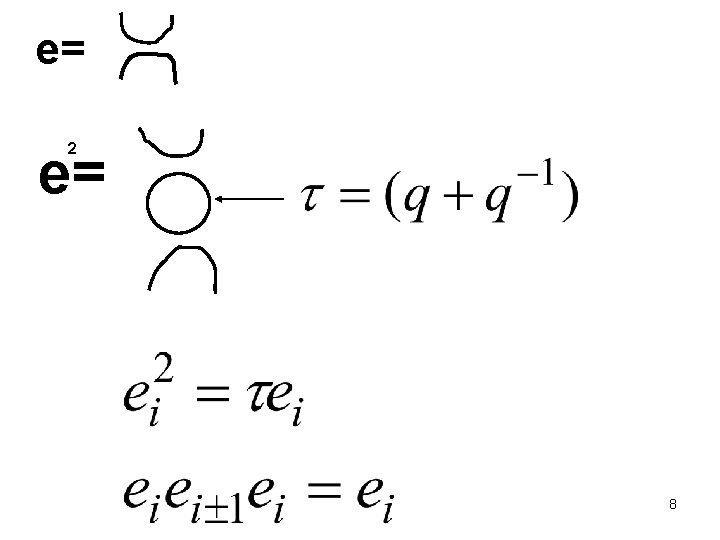




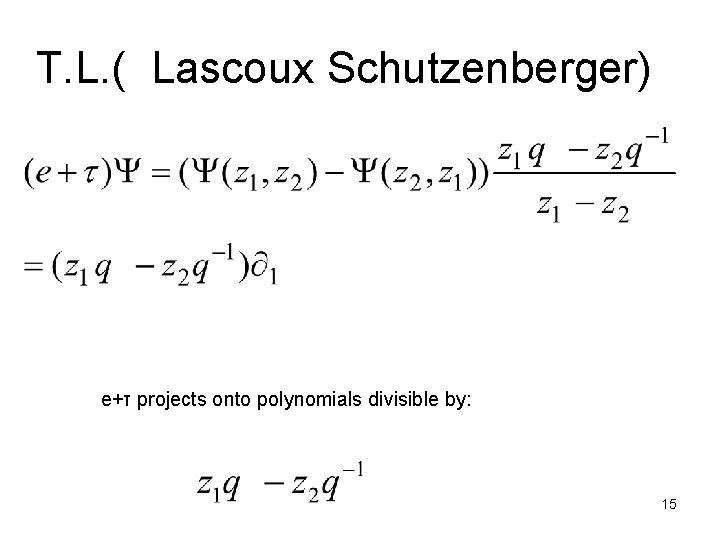
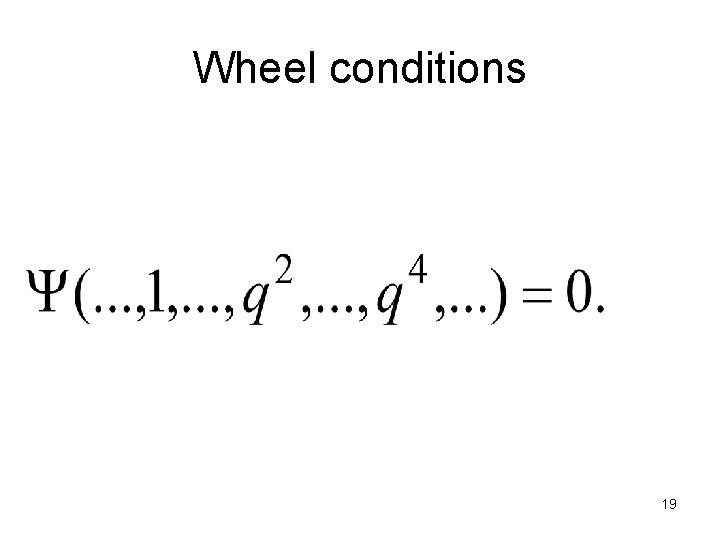














- Slides: 40

Razumov-Stroganov Vincent Pasquier Service de Physique Théorique C. E. A. Saclay France 1

Alternating sign matrices 2
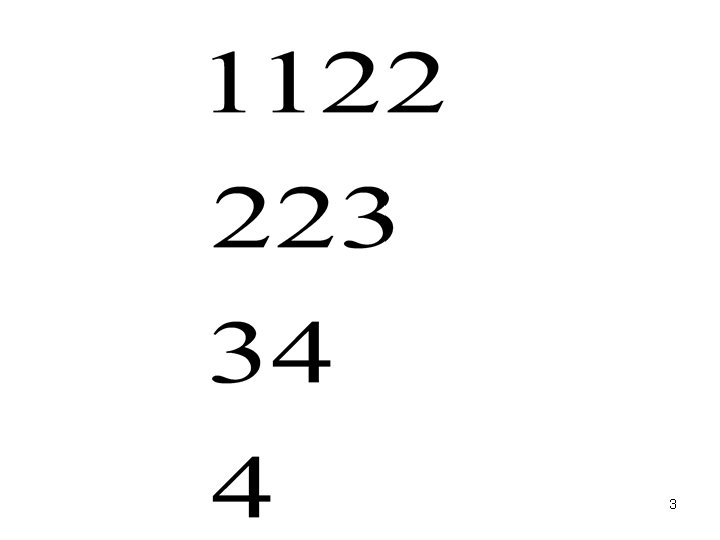
3

6 vertex model • • Replace the 0 by type a, b vertices. Replace +1, -1 by c vertices. Put apropriate boundary conditions. Give weight 1 to all vertices. 4

Can be computed exactly • Gaudin Izergin-Korepin determinant 5

In the case q =-1 3 • Partition function is symmetric in the variables qx, y. • Can be expressed as a Schur function • 00112233…. Wheel condition z, q 2 z 6

Evaluate Schur function at z=1: 7
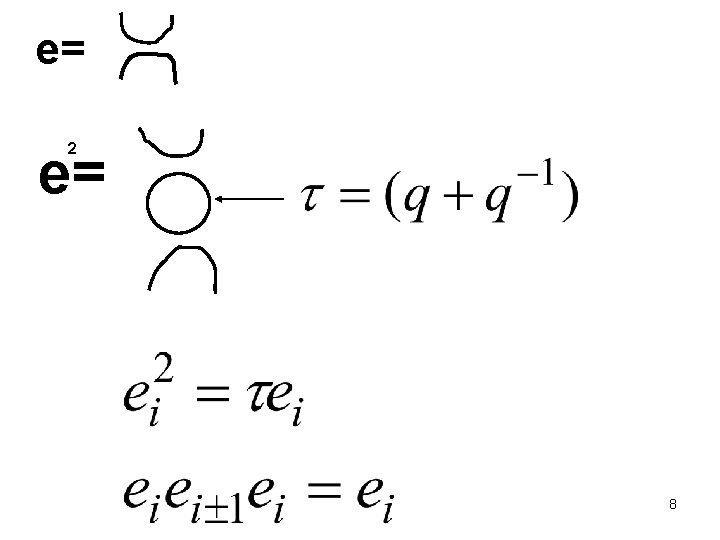
e= e= 2 8

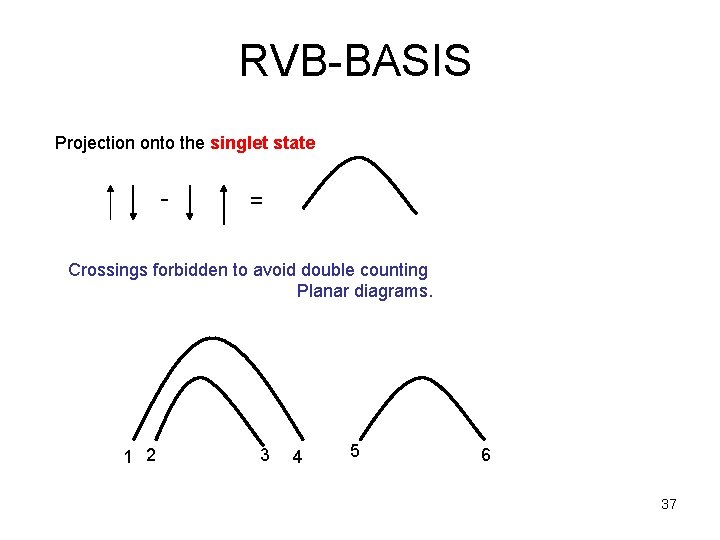
RVB basis: Projection onto the singlet state 9

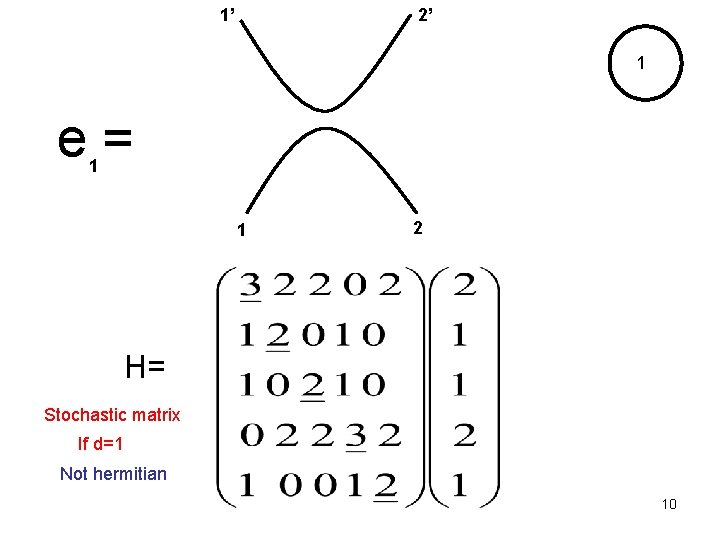
1’ 2’ 1 e= 1 1 2 H= Stochastic matrix If d=1 Not hermitian 10

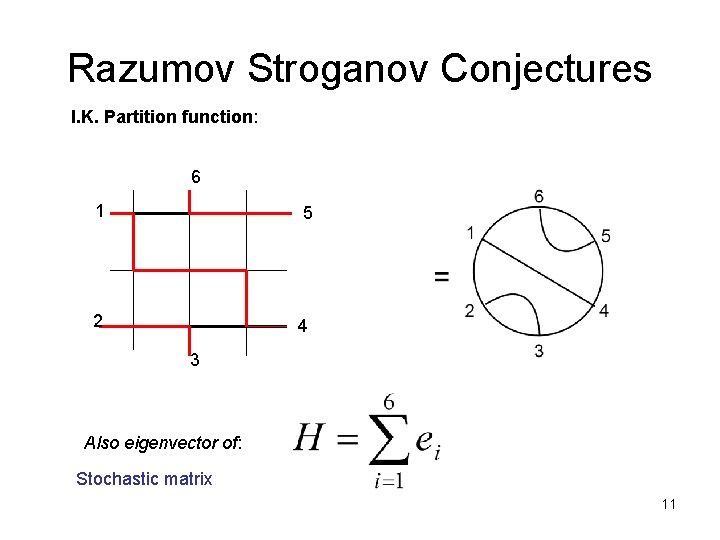
Razumov Stroganov Conjectures I. K. Partition function: 6 1 5 2 4 3 Also eigenvector of: Stochastic matrix 11

Transfer Matrix Consider inhomogeneous transfer matrix: L= + 12

Transfer Matrix Di Francesco Zinn-justin. 13

Vector indices are patterns, entries are polynomials in z , …, z 1 n Bosonic condition 14
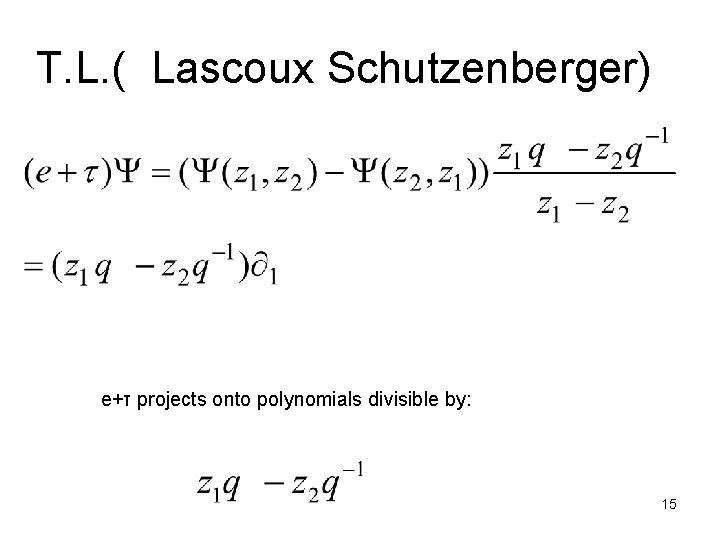
T. L. ( Lascoux Schutzenberger) e+τ projects onto polynomials divisible by: 15

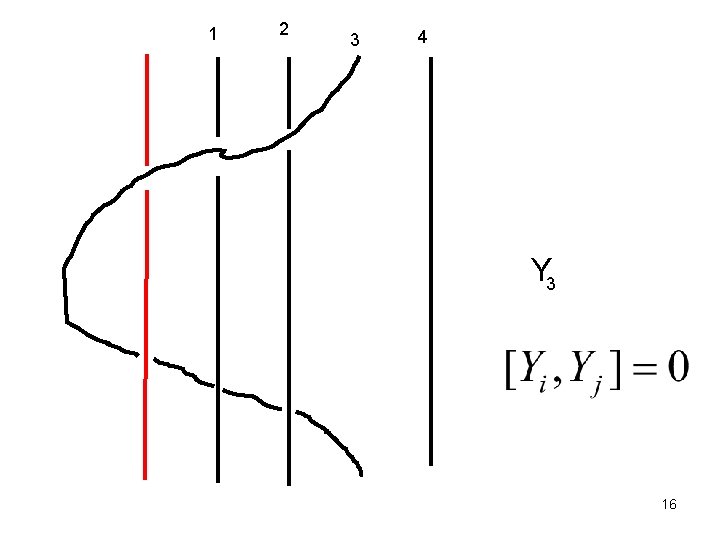
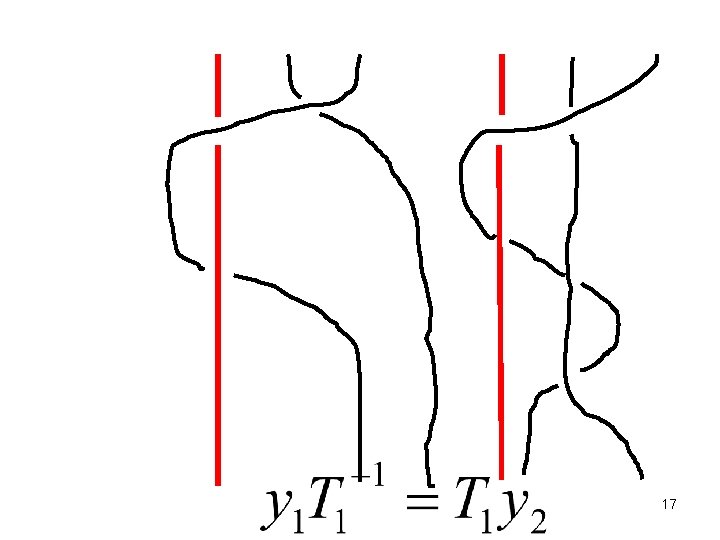
1 2 3 4 Y 3 16

17

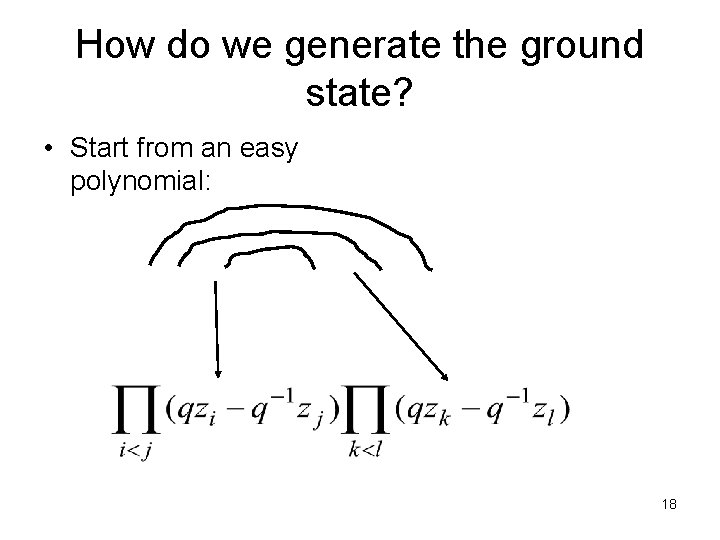
How do we generate the ground state? • Start from an easy polynomial: 18
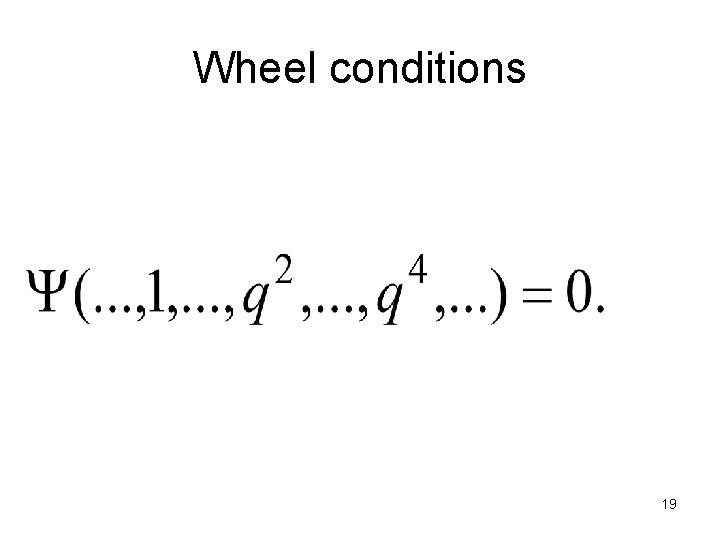
Wheel conditions 19

Evaluation? 20

Conjectures generalizing R. S. • Evaluation of these polynomials at z=1 have positive integer coefficients in d: 21

q-deformation • RVB basis has a natural q-deformation known as the Kazhdan Lusztig basis. • Jack polynomials have a natural deformation Macdonald polynomials. • Evaluation at z=1 of Macdonald polynomials in the KL basis have mysterious positivity properties. 22

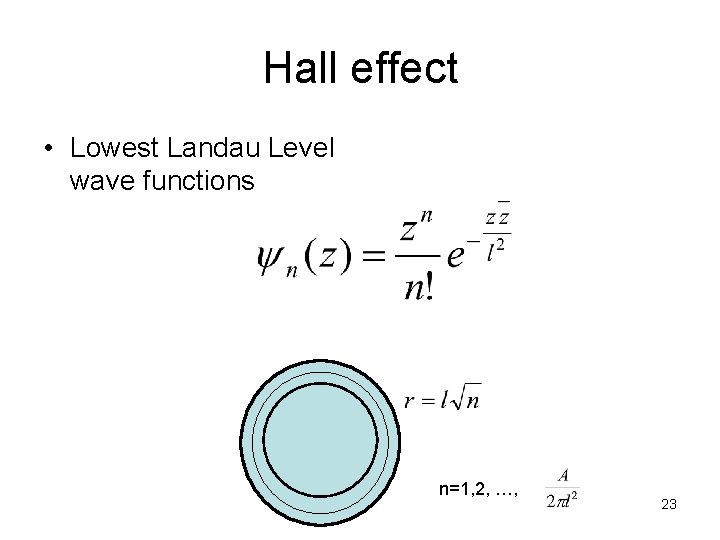
Hall effect • Lowest Landau Level wave functions n=1, 2, …, 23

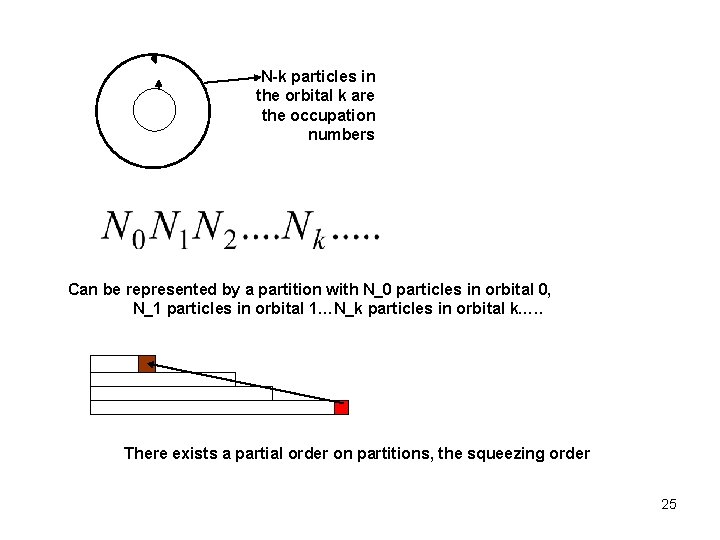
Number of available cells also the maximal degree in each variable Is a basis of states for the system Labeled by partitions 24

N-k particles in the orbital k are the occupation numbers Can be represented by a partition with N_0 particles in orbital 0, N_1 particles in orbital 1…N_k particles in orbital k…. . There exists a partial order on partitions, the squeezing order 25

Interactions translate into repulsion between particles. m universal measures the strength of the interactions. Competition between interactions which spread electrons apart and high compression which minimizes the degree n. Ground state is the minimal degree symmetric polynomial compatible with the repulsive interaction. 26

Laughlin wave function occupation numbers: Keeping only the dominant weight of the expansion 1 particle at most into m orbitals (m=3 here). 27

Important quantum number with a topological interpretation • Filling factor equal to number of particles per unit cell: • Number of variables Degree of polynomial In the preceding case. 28

Jack Polynomials: Jack polynomials are eigenstates of the Calogero. Sutherland Hamiltonian on a circle with 1/r^2 potential interaction. 29

Jack polynomials at Feigin-Jimbo-Miwa-Mukhin Generate ideal of polynomials“vanishing as the r power of the Distance between particles ( difference Between coordinates) as k+1 particles come together. 30

Exclusion statistics: • No more than k particles into r consecutive orbitals. For example when k=r=2, the possible ground states (most dense packings) are given by: 2020…. 1111…. . 0202…. . Filling factor is 31

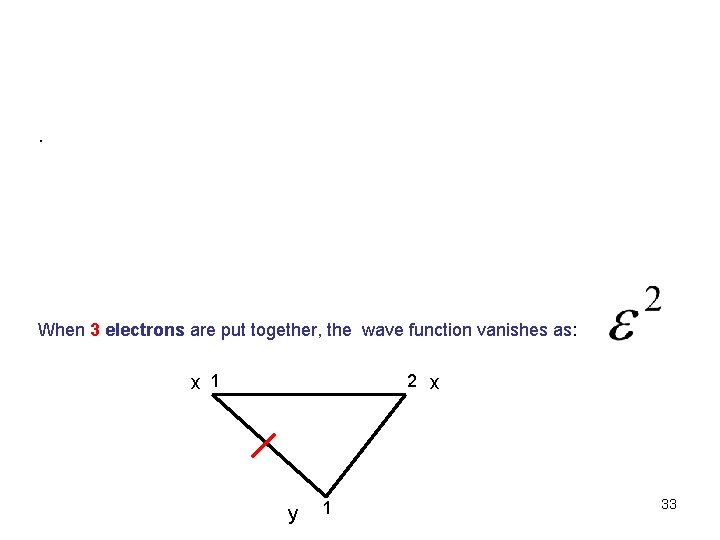
Moore Read (k=r=2) When 3 electrons are put together, the wave function vanishes as: 32

. When 3 electrons are put together, the wave function vanishes as: x 1 2 x y 1 33

Non symmetric polynomials • When additional degrees of freedom are present like spin, it is necessary to consider nonsymmetric polynomials. • A theory of nonsymmetric Jack polynomials exists with similar vanishing conditions. 34

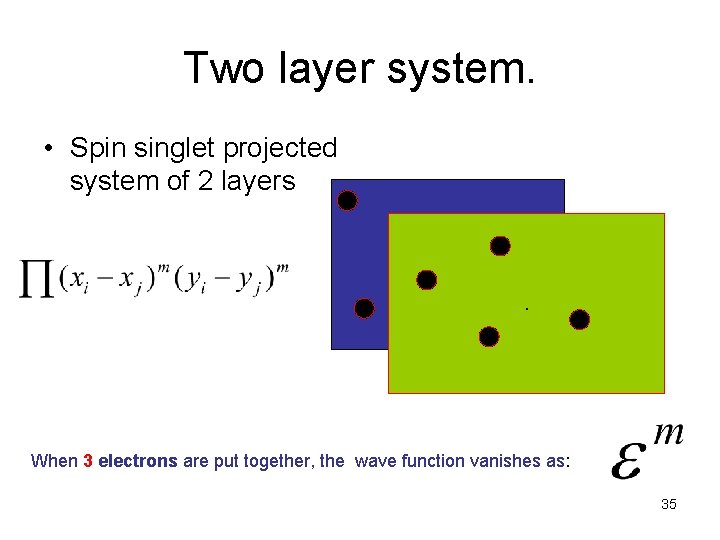
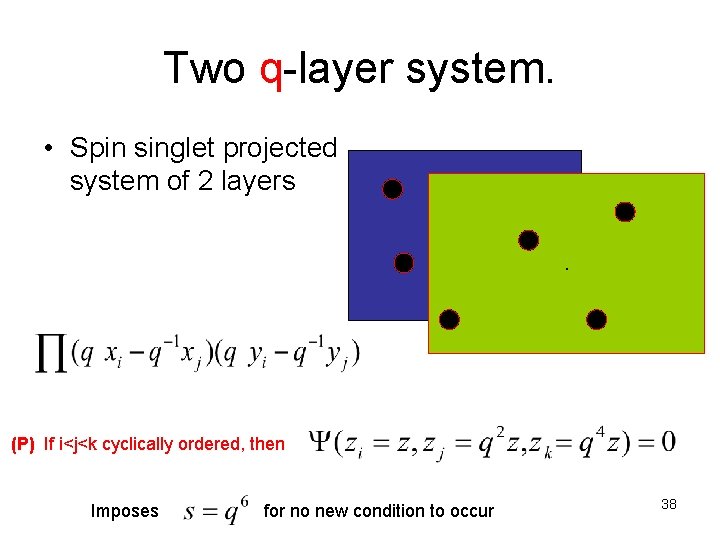
Two layer system. • Spin singlet projected system of 2 layers . When 3 electrons are put together, the wave function vanishes as: 35

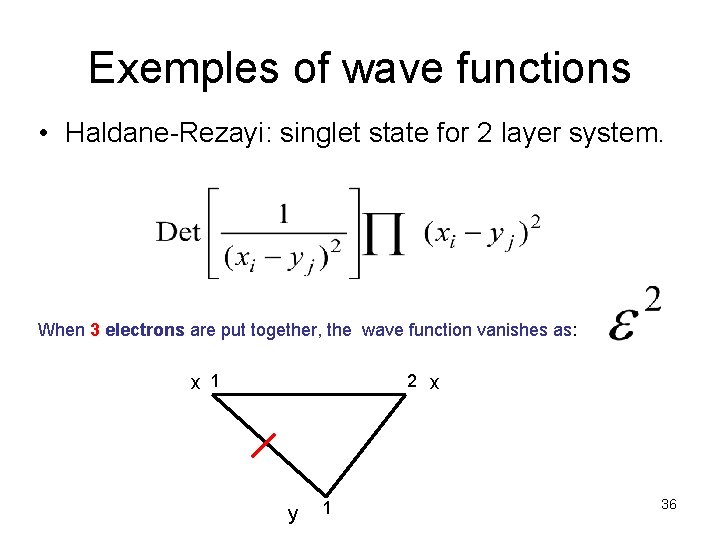
Exemples of wave functions • Haldane-Rezayi: singlet state for 2 layer system. When 3 electrons are put together, the wave function vanishes as: x 1 2 x y 1 36

RVB-BASIS Projection onto the singlet state - = Crossings forbidden to avoid double counting Planar diagrams. 1 2 3 4 5 6 37

Two q-layer system. • Spin singlet projected system of 2 layers. (P) If i<j<k cyclically ordered, then Imposes for no new condition to occur 38

Other generalizations • q-Haldane-Rezayi Generalized Wheel condition, Gaudin Determinant Related in some way to the Izergin-Korepin partition function? Fractional hall effect Flux ½ electron 39

Conclusions • T. Q. F. T. realized on q-deformed wave functions of the Hall effect. • All connected to Razumov-Stroganov type conjectures. • Relations with works of Feigin, Jimbo, Miwa, Mukhin and Kasatani on polynomials obeying wheel condition. • Understand excited states (higher degree polynomials) of the Hall effect. 40
 Christelle pasquier
Christelle pasquier Marjolaine pasquier
Marjolaine pasquier Physique chimie
Physique chimie 6 transformation physique
6 transformation physique Physique
Physique Les types de muscles
Les types de muscles Le portrait physique
Le portrait physique Musique chimie
Musique chimie Physique chimie terminale
Physique chimie terminale Transceivers ethernet à couche physique
Transceivers ethernet à couche physique Programme première sti2d physique-chimie
Programme première sti2d physique-chimie Physique chimie
Physique chimie Calcul de la productivite
Calcul de la productivite Dr rezzan khan
Dr rezzan khan Agent antimicrobien physique exemple
Agent antimicrobien physique exemple Physique
Physique Pfs physique
Pfs physique Transceivers ethernet à couche physique
Transceivers ethernet à couche physique Acromégalie célébrités
Acromégalie célébrités Mouvement de masse
Mouvement de masse Grandeur physique vectorielle
Grandeur physique vectorielle Les types de servuction
Les types de servuction Filiere tpc
Filiere tpc Types de forces physique
Types de forces physique Harfang des neiges description physique
Harfang des neiges description physique Iz pronunciation
Iz pronunciation Physique chimie
Physique chimie Grandeurs fondamentales
Grandeurs fondamentales Physique
Physique Les 5 composantes de la condition physique
Les 5 composantes de la condition physique Physique
Physique Exercice physique descente en rappel
Exercice physique descente en rappel Couche physique osi
Couche physique osi Transceivers ethernet à couche physique
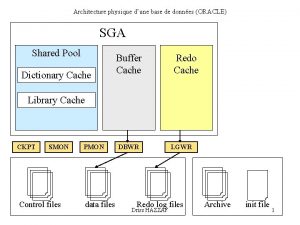
Transceivers ethernet à couche physique Oracle smon
Oracle smon Préparation physique patinage artistique
Préparation physique patinage artistique Manifestation physique
Manifestation physique Carte physique
Carte physique Oem physique
Oem physique Physique chimie
Physique chimie Besoin physique
Besoin physique