QHE ASM Vincent Pasquier Service de Physique Thorique














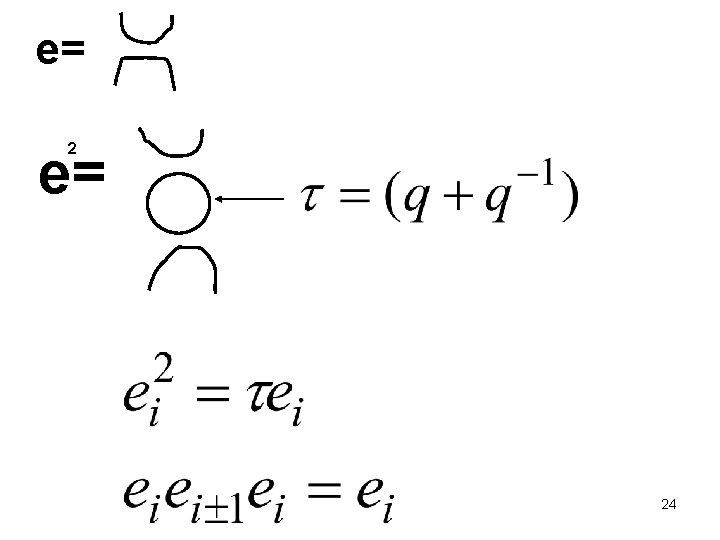








- Slides: 35

QHE, ASM Vincent Pasquier Service de Physique Théorique C. E. A. Saclay France 1

From the Hall Effect to integrability 1. Hall effect. 2. Annular algebras. 3. deformed Hall effect and ASM. 2

Most striking occurrence of a quantum macroscopic effect in the real word • In presence of of a magnetic field, the conductivity is quantized to be a simple fraction up to • Important experimental fractions for electrons are: • Theorists believe for bosons: • Fraction called filling factor. 3

Hall effect • Lowest Landau Level wave functions n=1, 2, …, 4

Number of available cells also the maximal degree in each variable Is a basis of states for the system Labeled by partitions 5

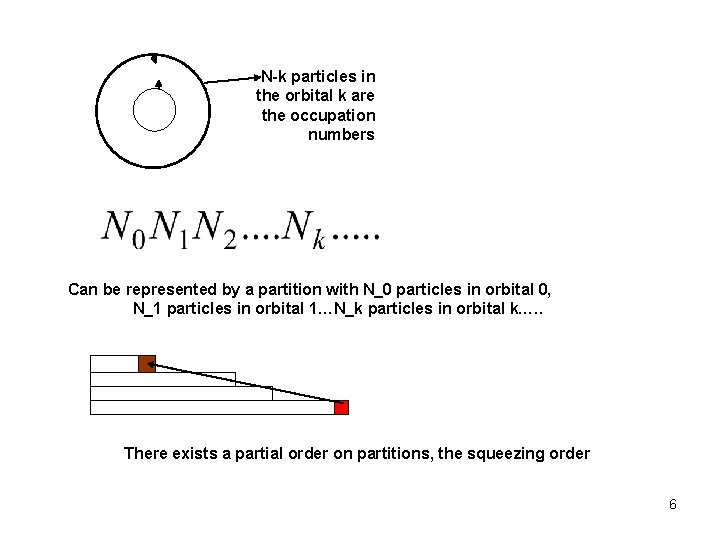
N-k particles in the orbital k are the occupation numbers Can be represented by a partition with N_0 particles in orbital 0, N_1 particles in orbital 1…N_k particles in orbital k…. . There exists a partial order on partitions, the squeezing order 6

Interactions translate into repulsion between particles. m universal measures the strength of the interactions. Competition between interactions which spread electrons apart and high compression which minimizes the degree n. Ground state is the minimal degree symmetric polynomial compatible with the repulsive interaction. 7

Laughlin wave function occupation numbers: Keeping only the dominant weight of the expansion 1 particle at most into m orbitals (m=3 here). 8

Important quantum number with a topological interpretation • Filling factor equal to number of particles per unit cell: • Number of variables Degree of polynomial In the preceding case. 9

Jack Polynomials: Jack polynomials are eigenstates of the Calogero. Sutherland Hamiltonian on a circle with 1/r^2 potential interaction. 10

Jack polynomials at Feigin-Jimbo-Miwa-Mukhin Generate ideal of polynomials“vanishing as the r power of the Distance between particles ( difference Between coordinates) as k+1 particles come together. 11

Exclusion statistics: • No more than k particles into r consecutive orbitals. For example when k=r=2, the possible ground states (most dense packings) are given by: 2020…. 1111…. . 0202…. . Filling factor is 12

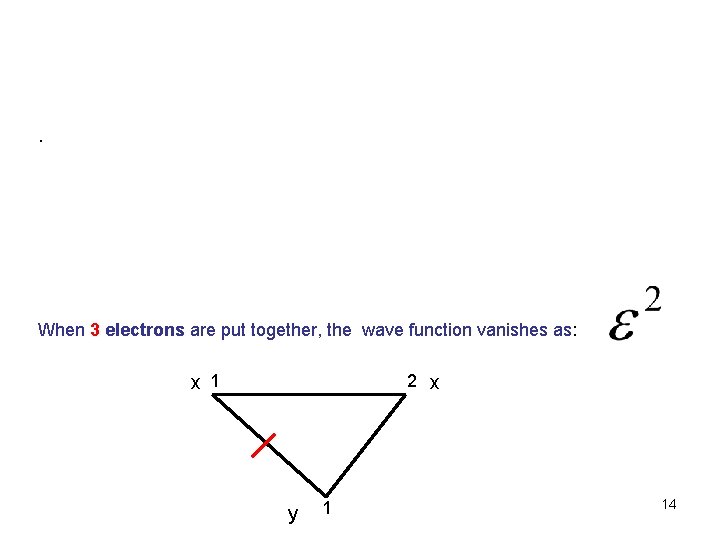
Moore Read (k=r=2) When 3 electrons are put together, the wave function vanishes as: 13

. When 3 electrons are put together, the wave function vanishes as: x 1 2 x y 1 14

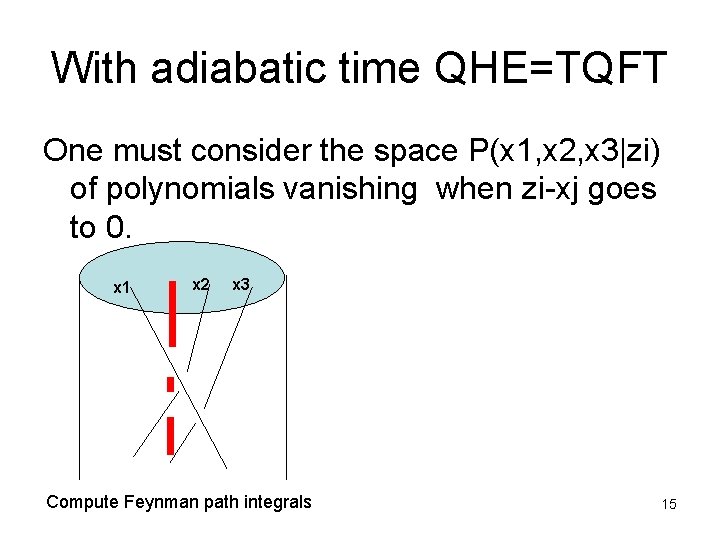
With adiabatic time QHE=TQFT One must consider the space P(x 1, x 2, x 3|zi) of polynomials vanishing when zi-xj goes to 0. x 1 x 2 x 3 Compute Feynman path integrals 15

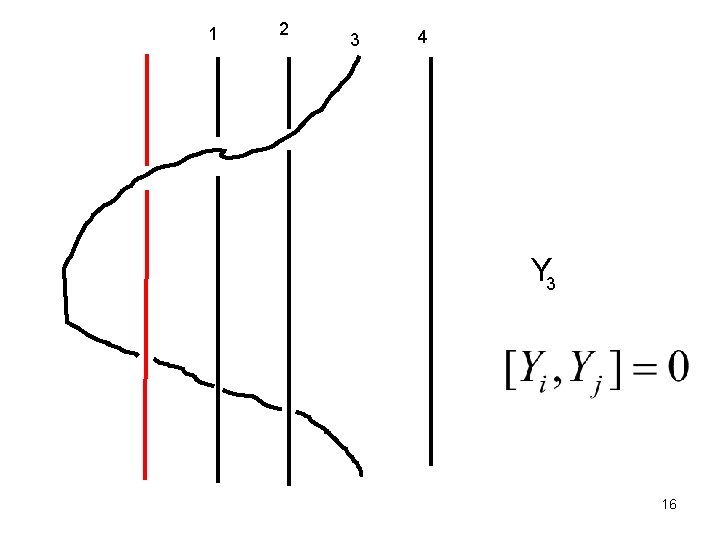
1 2 3 4 Y 3 16

17

Non symmetric polynomials • When additional degrees of freedom are present like spin, it is necessary to consider nonsymmetric polynomials. • A theory of nonsymmetric Jack polynomials exists with similar vanishing conditions. 18

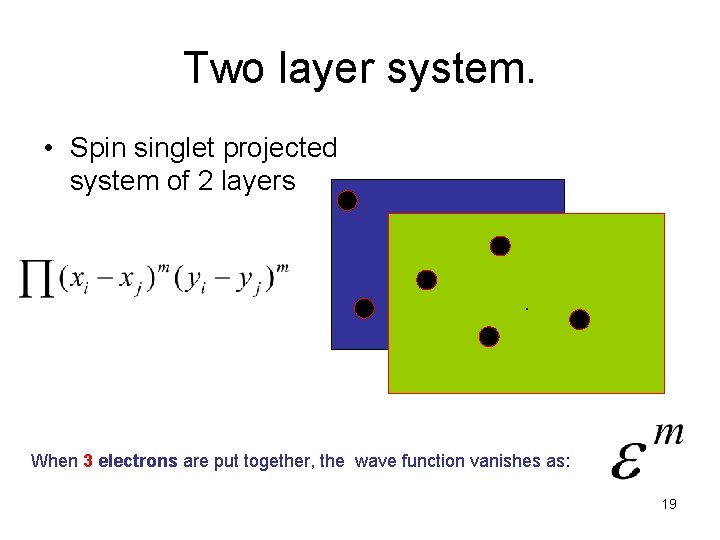
Two layer system. • Spin singlet projected system of 2 layers . When 3 electrons are put together, the wave function vanishes as: 19

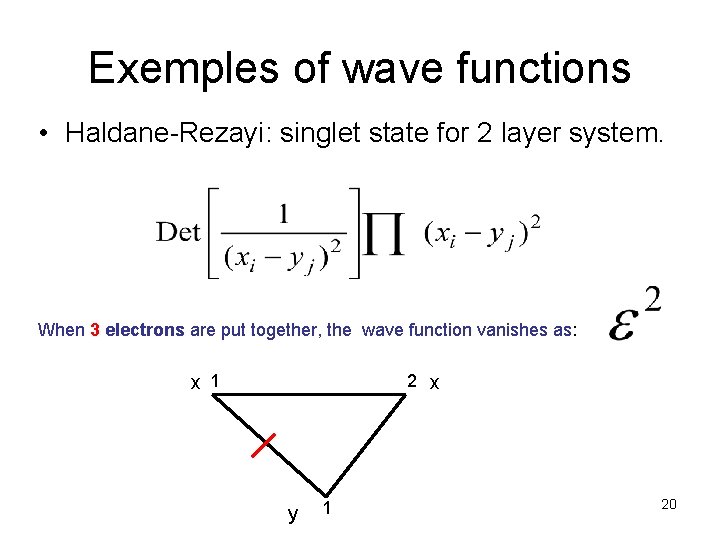
Exemples of wave functions • Haldane-Rezayi: singlet state for 2 layer system. When 3 electrons are put together, the wave function vanishes as: x 1 2 x y 1 20

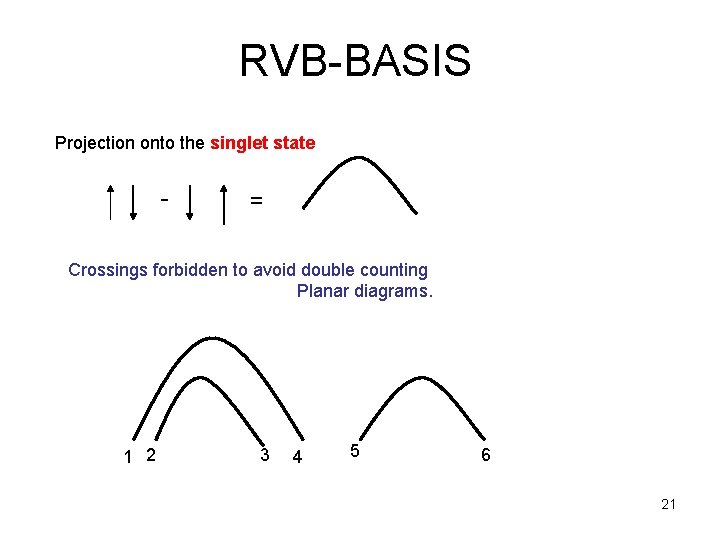
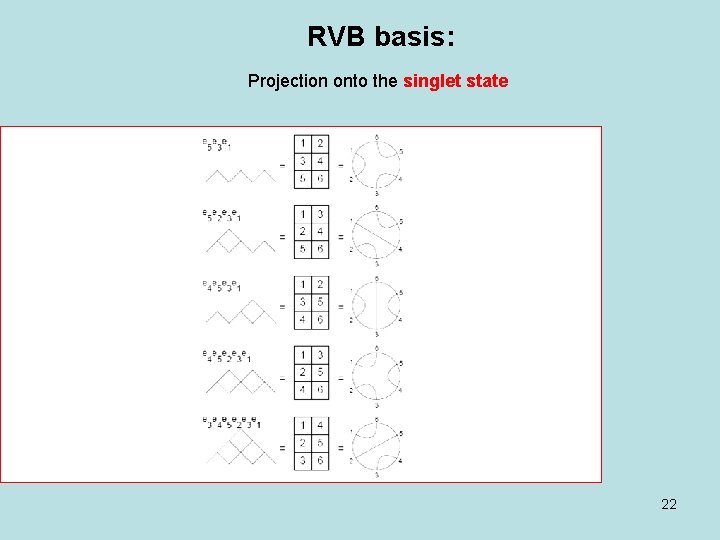
RVB-BASIS Projection onto the singlet state - = Crossings forbidden to avoid double counting Planar diagrams. 1 2 3 4 5 6 21

RVB basis: Projection onto the singlet state 22

q-deformation • RVB basis has a natural q-deformation known as the Kazhdan Lusztig basis. • Jack polynomials have a natural deformation Macdonald polynomials. • Evaluation at z=1 of Macdonald polynomials in the KL basis have mysterious positivity properties. 23
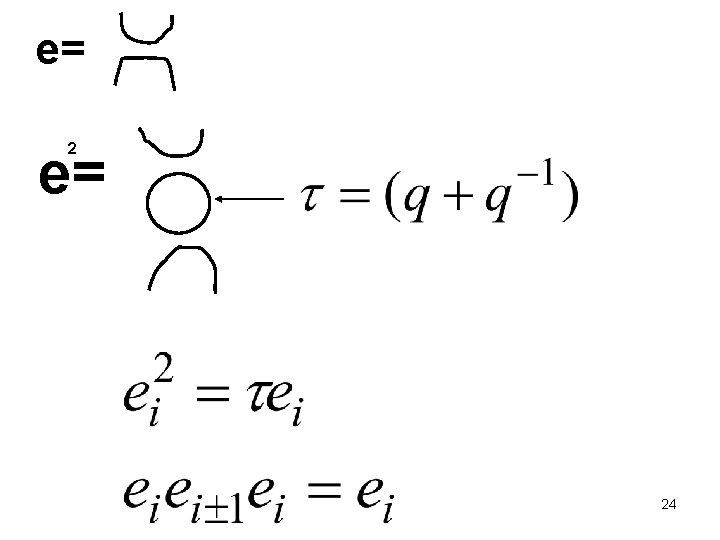
e= e= 2 24

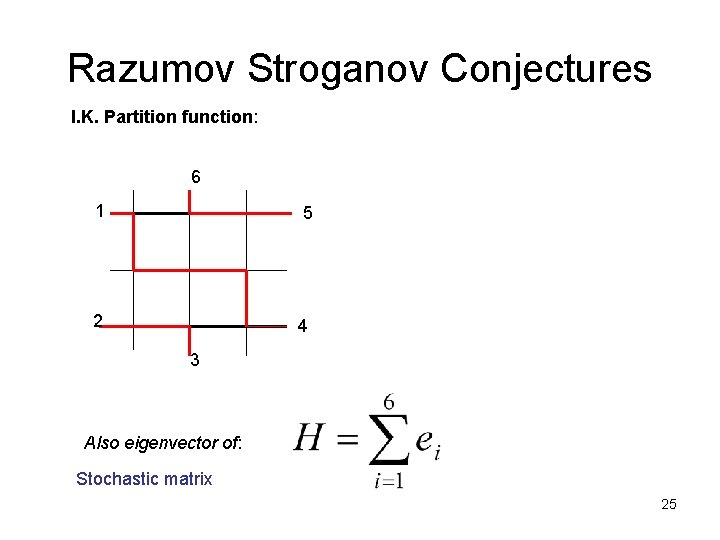
Razumov Stroganov Conjectures I. K. Partition function: 6 1 5 2 4 3 Also eigenvector of: Stochastic matrix 25

1’ 2’ 1 e= 1 1 2 H= Stochastic matrix If d=1 Not hermitian 26

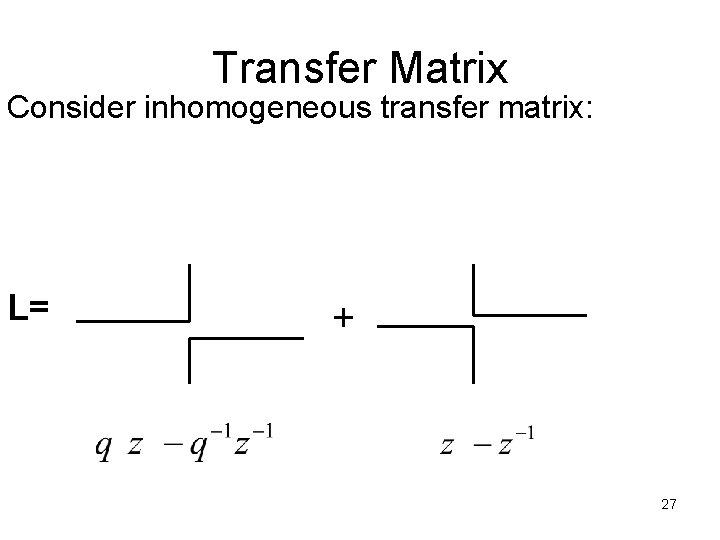
Transfer Matrix Consider inhomogeneous transfer matrix: L= + 27

Transfer Matrix Di Francesco Zinn-justin. 28

Vector indices are patterns, entries are polynomials in z , …, z 1 n Bosonic condition 29

T. L. ( Lascoux Schutzenberger) e+τ projects onto polynomials divisible by: e Measures the Amplitude for 2 electrons to be In the same layer 30

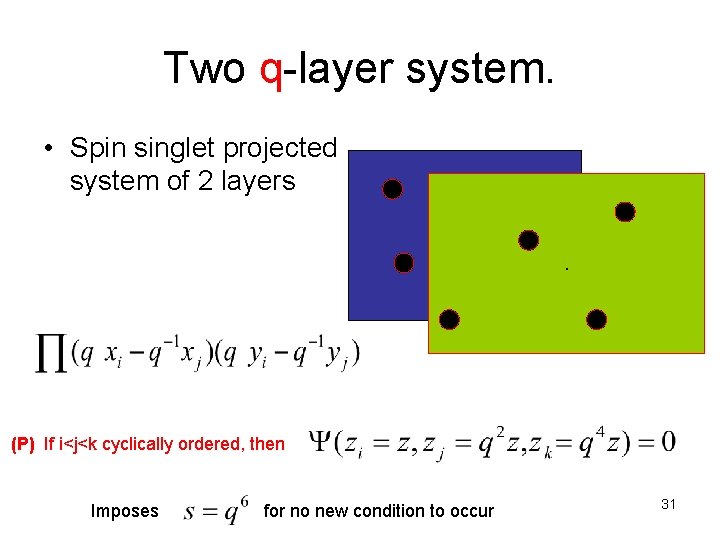
Two q-layer system. • Spin singlet projected system of 2 layers. (P) If i<j<k cyclically ordered, then Imposes for no new condition to occur 31

Conjectures generalizing R. S. • Evaluation of these polynomials at z=1 have positive integer coefficients in d: 32

Other generalizations • q-Haldane-Rezayi Generalized Wheel condition, Gaudin Determinant Related in some way to the Izergin-Korepin partition function? Fractional hall effect Flux ½ electron 33

Moore-Read • Property (P) with s arbitrary. • Affine Hecke replaced by Birman-Wenzl. Murakami, . • R. S replaced by Nienhuis De Gier in the symmetric case. 34

Conclusions • T. Q. F. T. realized on q-deformed wave functions of the Hall effect. • All connected to Razumov-Stroganov type conjectures. • Relations with works of Feigin, Jimbo, Miwa, Mukhin and Kasatani on polynomials obeying wheel condition. • Understand excited states (higher degree polynomials) of the Hall effect. 35
 Asm
Asm Jainendra k. jain
Jainendra k. jain Qhe
Qhe Qhe
Qhe Marjolaine pasquier
Marjolaine pasquier Christelle pasquier
Christelle pasquier Jason laberge
Jason laberge ä34
ä34 Asm and
Asm and Asm microbelibrary.org
Asm microbelibrary.org Orimux
Orimux Asm division
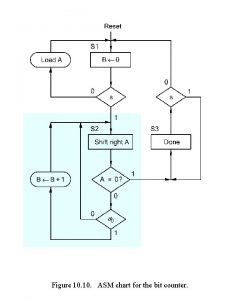
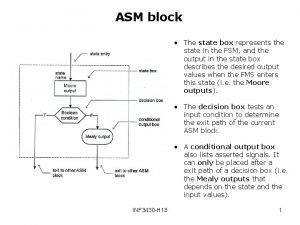
Asm division An asm chart of mealy model
An asm chart of mealy model Asm chart
Asm chart Mul asm
Mul asm Plusportals/asm
Plusportals/asm Asm basics
Asm basics Streptococcus pyogenes morphology
Streptococcus pyogenes morphology Bacterial capsul
Bacterial capsul Alt asm lean framework
Alt asm lean framework Facial expression recognition
Facial expression recognition Mult.asm
Mult.asm Asm chart is composed of
Asm chart is composed of Asm encoder
Asm encoder Ipam windows server 2008
Ipam windows server 2008 One flip flop per state method
One flip flop per state method Aircraft reliability program manual
Aircraft reliability program manual Search photos by face
Search photos by face Continues
Continues Asm chart
Asm chart Asm
Asm Mealy asm chart
Mealy asm chart State box of asm chart represents
State box of asm chart represents Asm 11
Asm 11 Addsub.asm
Addsub.asm Asm microbelibrary
Asm microbelibrary