R G NAZMITDINOV Elements of Random Matrix Theory

R. G. NAZMITDINOV Elements of Random Matrix Theory and chaos-order transition in finite quantum systems 1

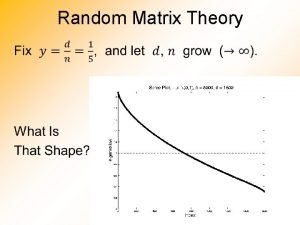
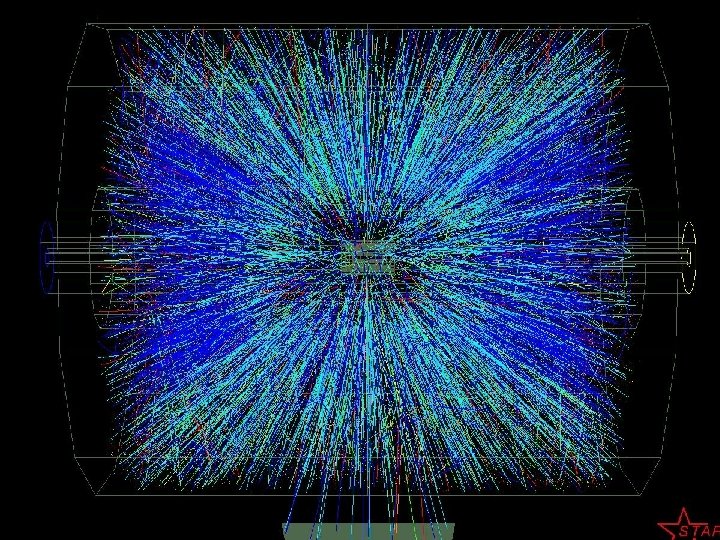
1. Motivation When we pass from hadron-light nucleus, light nucleus-light nucleus collisions at low, middle and high energies to relativistic and ultrarelativistic heavy ion collisions we get the new and unequal possibility: to create the high density and high temperature hadronic matter and to get the information on the properties of the matter under extreme conditions. In such new situation the volume of information increases sharply as well as the background information. The Figure illustrates how the volume of the information increase with energy and the mass of beams. Some time the background information From hadron-light nucleus, light nucleus-light nucleus collisions at low, medium and high energies to relativistic and ultrarelativistic heavy ion collisions we create a hadronic matter at high extreme conditions. In such new situation the volume of information increases drastically. A natural question arises as to how identify the useful signal that would be unambiguously associated with a certain physical process ? , p +p, A Pb+Pb √s. NN = 17. 3 Ge. V NA 49 SPS CERN Au+Au √s. NN = 200 Ge. V STAR RHIC BNL Pb. Pb √s. NN= 5. 5 Te. V Alice LHC CERN

3

• Statistical approach: recent theoretical analyses of the multiplicity fluctuations demonstrate that corresponding results are different in different ensembles and it is sensitive to conservation laws obeyed by a statistical system. • Transport theory: the underlying concept of transport models is based on numerical solution of the Boltzmann equation. However, exact numerical solutions, for example, of the BUU equation are very difficult to obtain and, therefore, various approximate treatments have been developed. The only proof is that numerical solutions provide the asymptotic limit at equilibrium, which can be deduced from the Boltzmann equation (the BUU equation without potential and Pauli-blocking factor)

• Equation of motion of the Brownian particle

Brownian motion model for the matrix H • Suppose that (Dyson, 1962) • We require that each H be a random variable

Standard statistical mechanics One considers an ensemble of identical physical systems, all governed by the same Hamiltonian but differing in initial conditions, and calculates thermo-dynamic functions by averaging over this ensemble. Wigner proposed to consider ensembles of dynamic systems governed by different Hamiltonians with some common symmetry property. A New Statistical Mechanics This novel statistical approach focuses attention on the generic properties which are common to all members of the ensemble and determined by the underlying fundamental symmetries. Each of the elements is a random variable. They are statistically independent of each other.

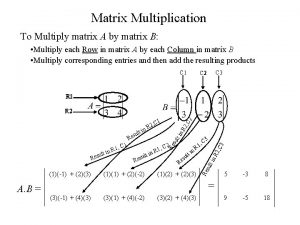
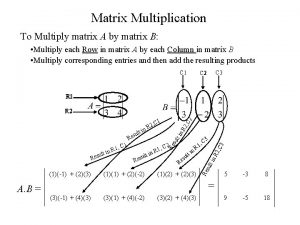
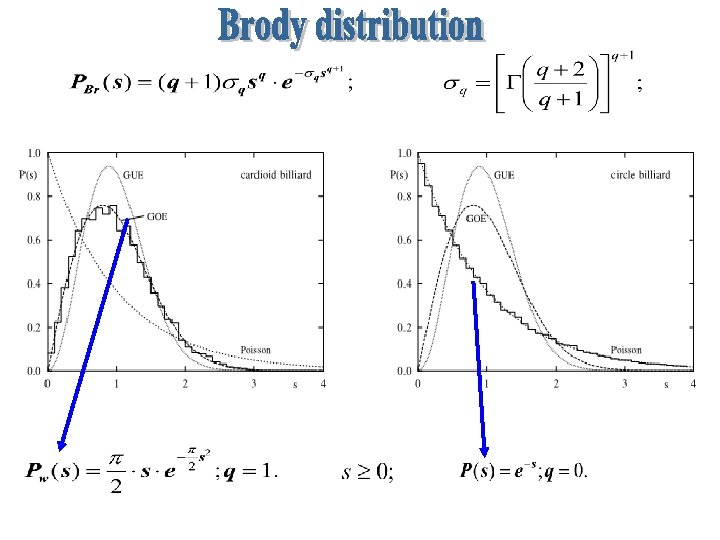
Joint probability of the independent matrix elements Joint probability of the eigen-values There are several useful statistical measures of spectral fluctuations. Among the most popular are nearest-neighbor spacing distributions P(s). Their asymptotic forms for large N cannot be written in a simple form, but they are surprisingly well approximated by the simple expressions obtained for N=2.

For A=0

Wigner distribution

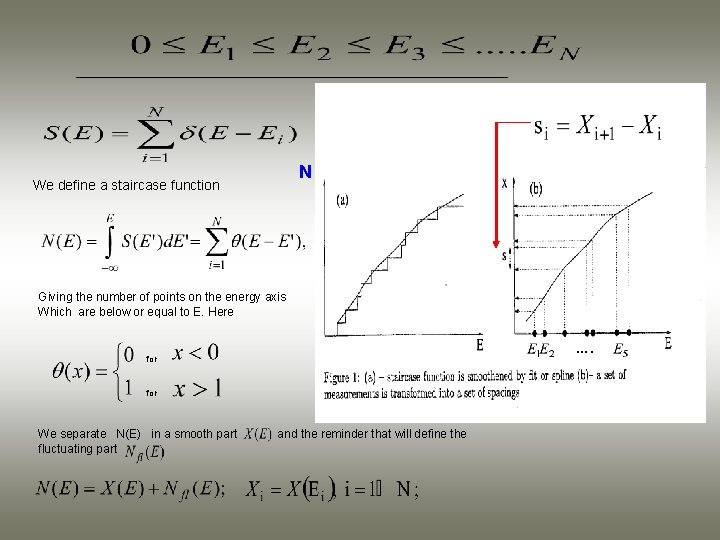
N We define a staircase function Giving the number of points on the energy axis Which are below or equal to E. Here …. for We separate N(E) in a smooth part fluctuating part and the reminder that will define the

Quantum chaos: the matrix is the Hamiltonian. Though the Hamiltonian is not random (it is given), it is observed and conjectured (but not understood) that (when the corresponding classical mechanical problem is chaotic), its spectrum has the same distribution as the spectrum of a random matrix. Random Hamiltonians belong to Gaussian ensembles, like GUE, GOE or GSE depending on their symmetries Disordered systems: the matrix is the Hamiltonian. It is naturally a random matrix due to disorder. We average over samples or over variations of an external parameter (a magnetic field). Again, the Hamiltonian can belong to Gaussian ensembles, like GUE, GOE or GSE depending on their symmetries

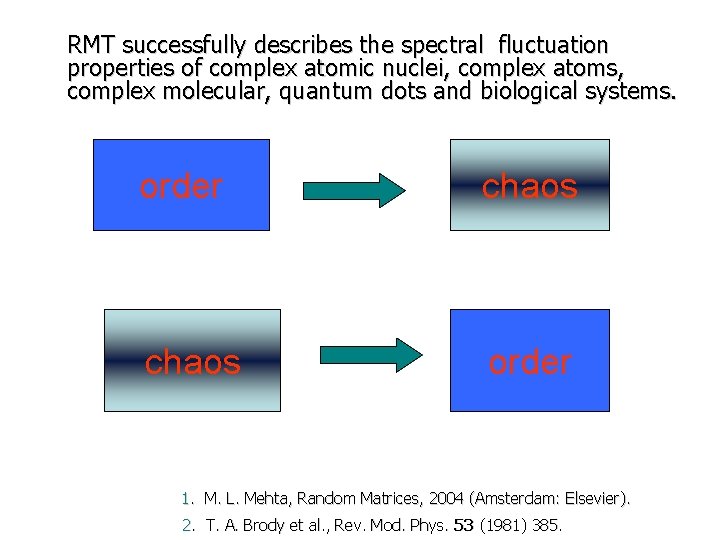
RMT successfully describes the spectral fluctuation properties of complextoatomic nuclei, complex atoms, complex molecular, quantum dots and biological systems. to order chaos order 1. M. L. Mehta, Random Matrices, 2004 (Amsterdam: Elsevier). 2. T. A. Brody et al. , Rev. Mod. Phys. 53 (1981) 385.

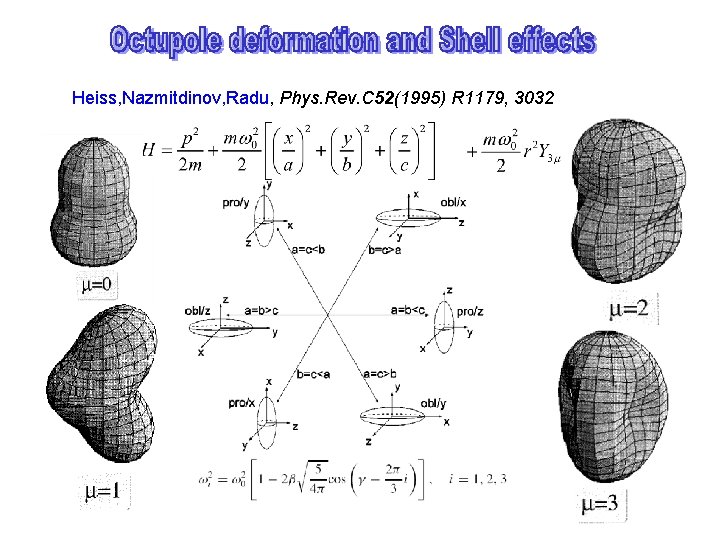
Heiss, Nazmitdinov, Radu, Phys. Rev. C 52(1995) R 1179, 3032

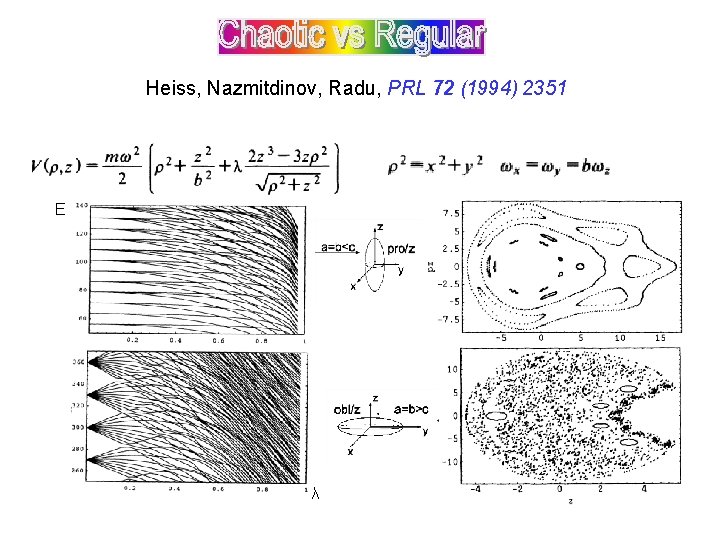
Heiss, Nazmitdinov, Radu, PRL 72 (1994) 2351 E λ

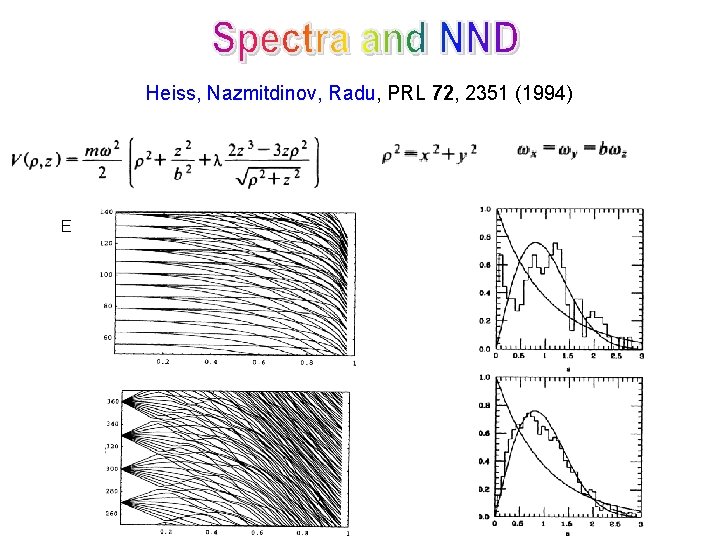
Heiss, Nazmitdinov, Radu, PRL 72, 2351 (1994) E λ

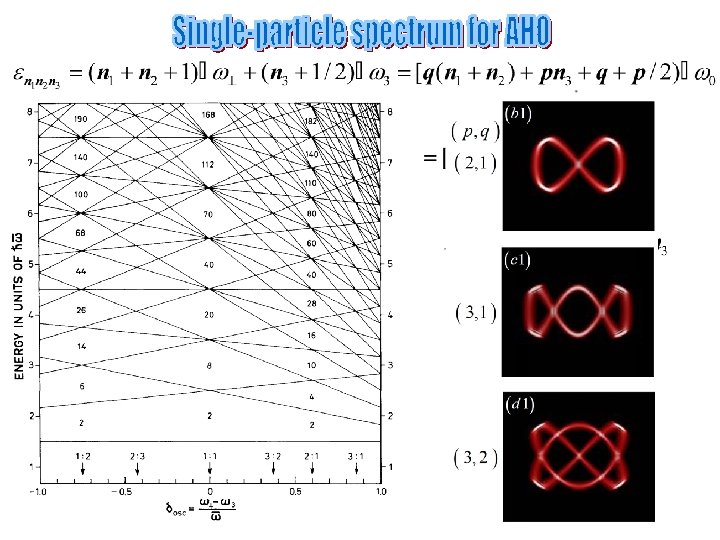
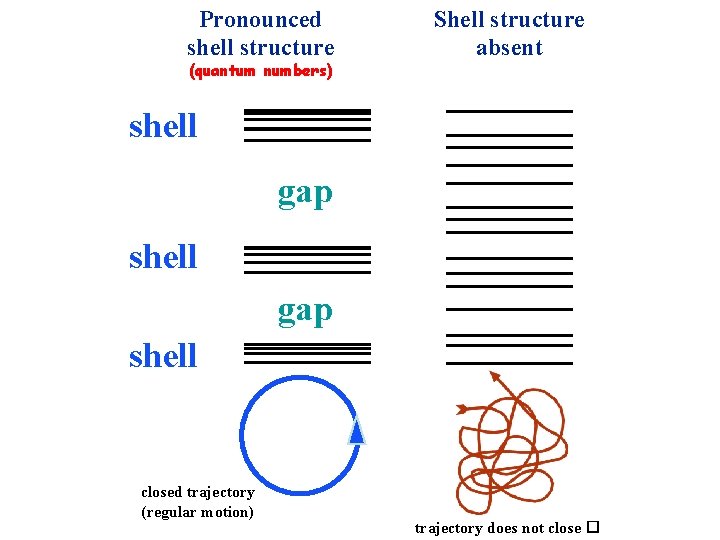
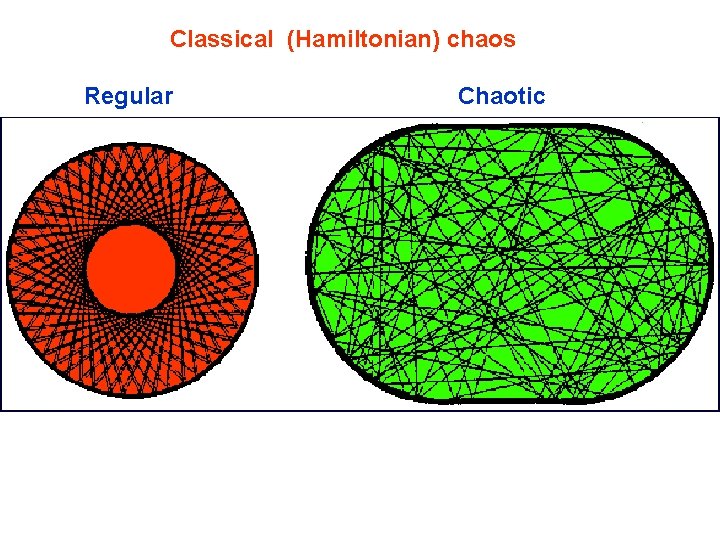
Pronounced shell structure (quantum numbers) Shell structure absent shell gap shell closed trajectory (regular motion) trajectory does not close �

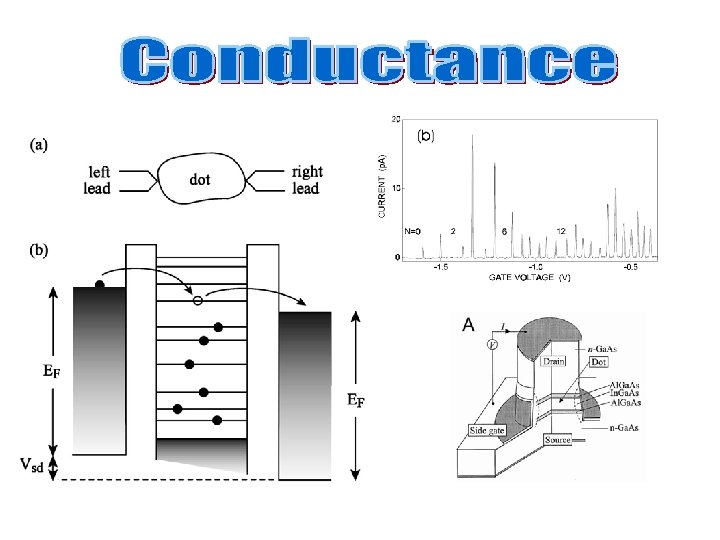
Quantum dots (QD) are small boxes (2 – 10 nm on a side, corresponding to 10 to 50 atoms in diameter), contained in semiconductor, and holding a number of electrons. If the carrier motion in a solid is limited in a layer of a thickness of the order of the carrier de Broglie wavelength (λ), one will observe effects of size quantization One can consider the QD as a tiny laboratories in which quantum and classical effects of electron-electron interaction can be studied. Mesoscopic system: quantum fluctuations are very important !

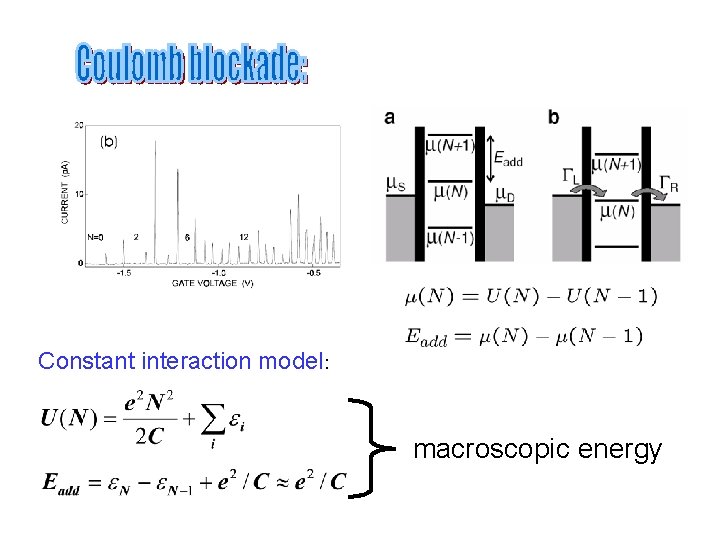
Constant interaction model: macroscopic energy

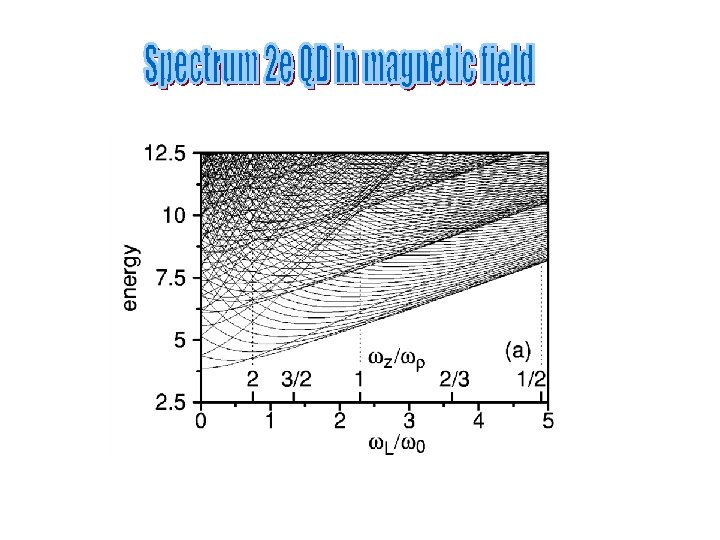
Dineykhan & Nazmitdinov, Phys. Rev. B 55 (1997) 13707 The Hamiltonian for the axially symmetric ( x = y 0) two-electron quantum dot in magnetic field reads

Introducing the relative r = r 1 - r 2 and center-of-mass R = (r 1+ r 2)/2 coordinates; the conjugated momenta P = M* d. R/dt, p = dr/dt, where M* = 2 m* and = m*/2, the Hamiltonian separates into the center-of-mass and relative-motion terms For a perpendicular magnetic field B|| z we choose the gauge and obtain where is the Larmor frequency.

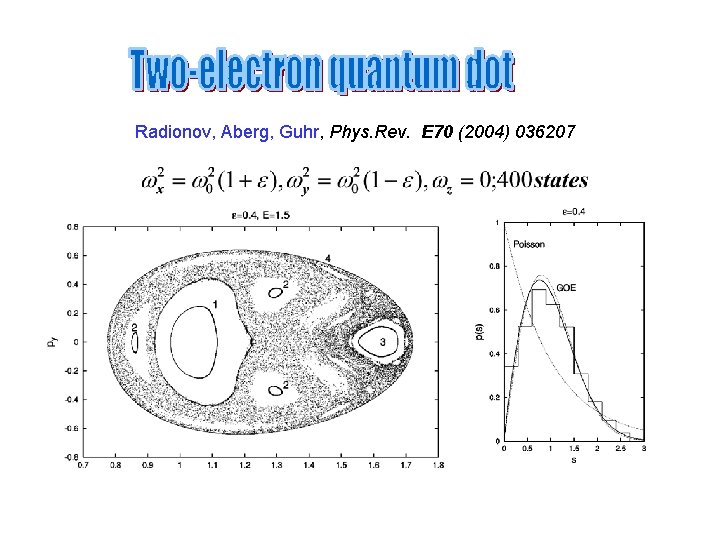
Radionov, Aberg, Guhr, Phys. Rev. E 70 (2004) 036207

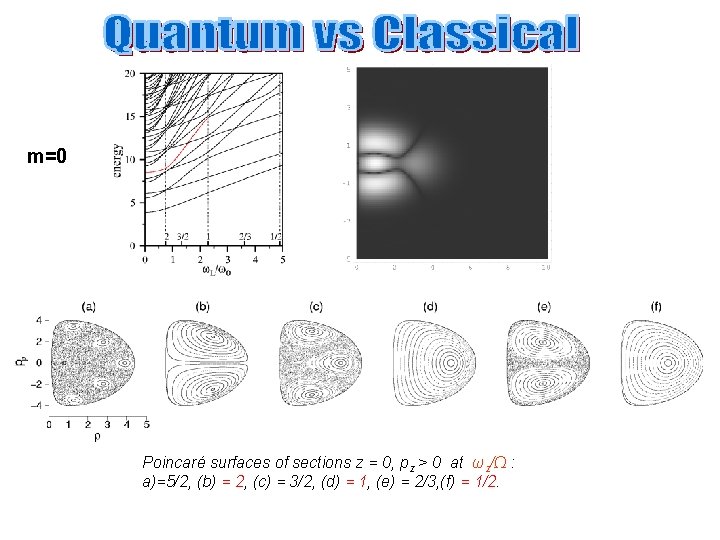
Simonović and Nazmitdinov, PRB 67 (2003) 041305(R) Poincaré surfaces of sections z = 0, pz > 0 of the classical relative motion of two electrons in an axially symmetric QD with: (a) ωz/Ω = 5/2, (b) ωz/Ω = 2, (c) ωz/Ω = 3/2, (d) ωz/Ω = 1, (e) ωz/Ω = 2/3 and (f) ωz/Ω = 1/2. The sections (b), (c) and (f) indicate that for the corresponding ratios ωz/Ω the system is integrable.

m=0 Poincaré surfaces of sections z = 0, pz > 0 at ωz/Ω : a)=5/2, (b) = 2, (c) = 3/2, (d) = 1, (e) = 2/3, (f) = 1/2.

Coulomb problem: V. A. Fock, Zs. f. Physik 98, 145 (1935)

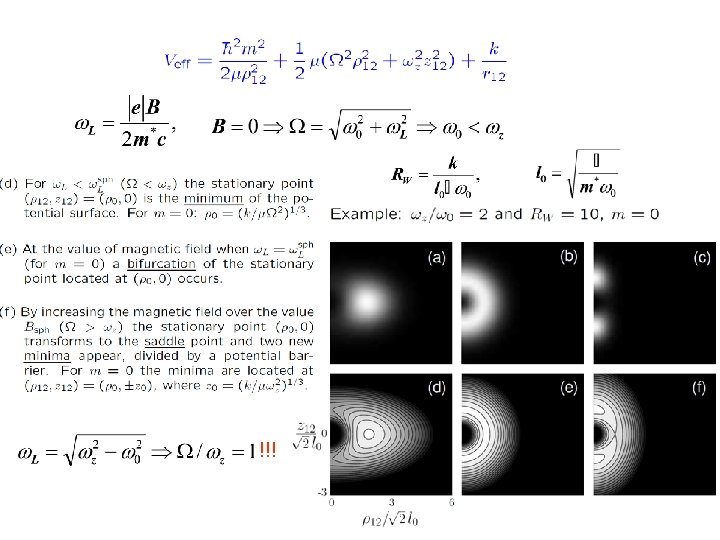
Simonović and Nazmitdinov, PRB 67 (2003) 041305(R) - For specific values of the ratio ωz/Ω the Hamiltonian Hrel (in the 3 D approach) becomes integrable !!! Beside the energy and , the additional integral of motion is and the problem has a spherical symmetry, O(3). New integrals of motion similar to Runge-Lentz vector are found at these specific values of magnetic field !

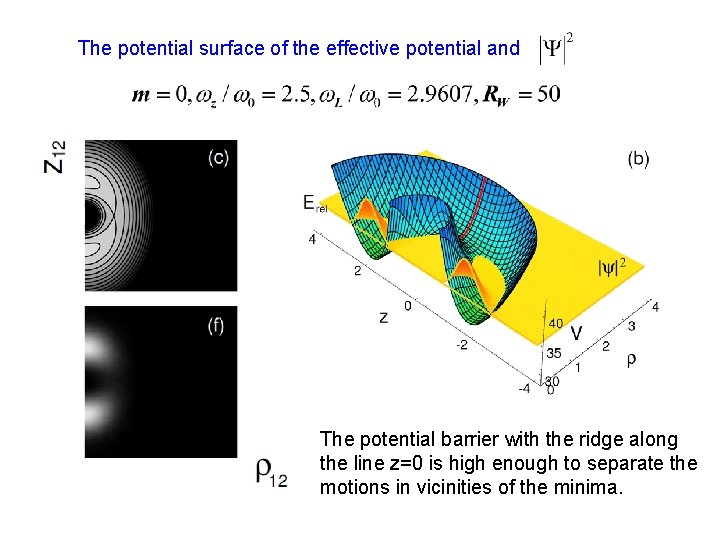
The potential surface of the effective potential and The potential barrier with the ridge along the line z=0 is high enough to separate the motions in vicinities of the minima.

Birman, Nazmitdinov, Yukalov, Phys. Rep. 526(2013)1

• QDs, as functioning elements for electronics or spintronics, should be able to carry through electrical and, possibly, spin current. Therefore, QD should be opened ! • Electronics, as well as future quantum computers are based on transmission and transformation (correction) of the shape of signals. This means that one has to be able to create the devices with predictable ability to transform non-linear characteristics. • The sensitivity of the dots to external magnetic field, can be made very different by making use of different shape (depth and width) of the confining potential.

Classical (Hamiltonian) chaos Regular Chaotic

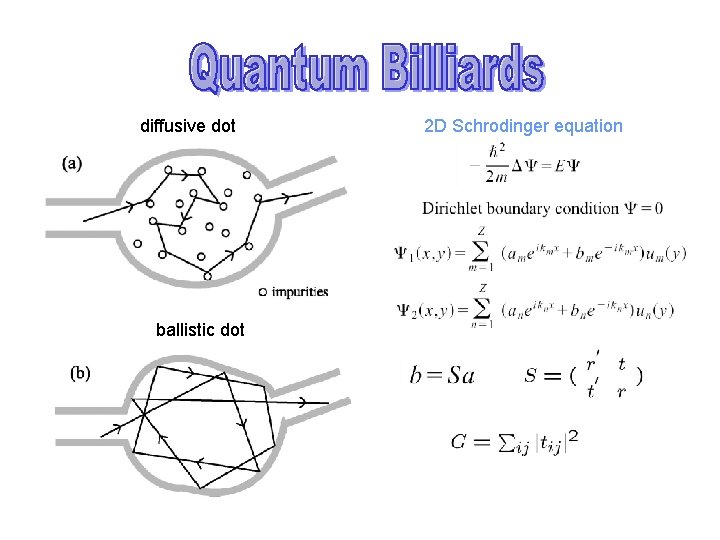
diffusive dot ballistic dot 2 D Schrodinger equation

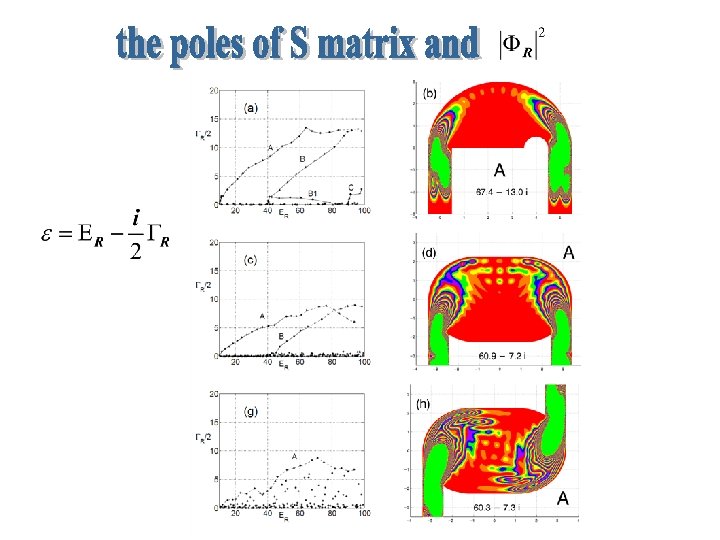
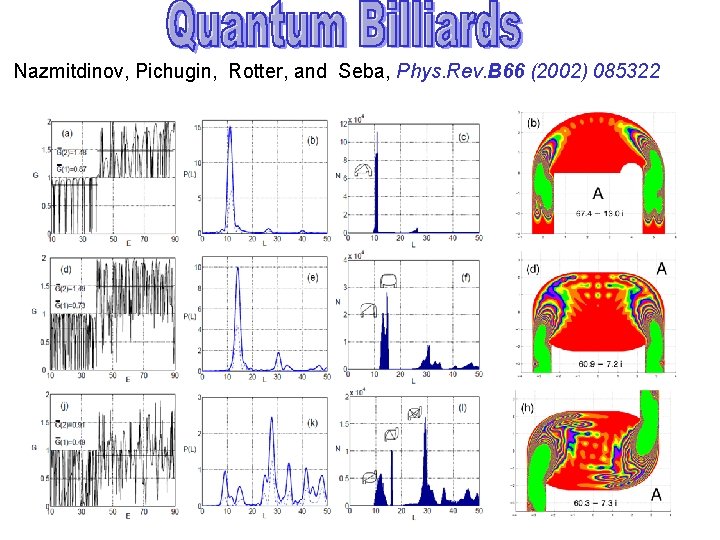
Nazmitdinov, Pichugin, Rotter, and Seba, Phys. Rev. B 66 (2002) 085322

Study of quantum correlations in finite quantum systems under external fields provide answers on fundamental aspects: symmetry breaking phenomena, stability of these systems, link between quantum and clasical description and nature of quantum coherence in transport. The RMT approach is free from various assumptions concerning the background of the measurements and it provides reliable information about correlations induced by external or internal perturbations