Pronsticos Series de Tiempo y Regresin Captulo 3

Pronósticos, Series de Tiempo y Regresión Capítulo 3: Regresión Lineal Simple 1

Temas o Modelo de Regresión Lineal Simple o Estimaciones puntuales de los mínimos o o o cuadrados Estimaciones puntuales y predicciones puntuales Suposiciones del modelo y el error estándar Prueba de la significancia de la pendiente y la ordenada al origen Intervalos de confianza y de predicción Coeficientes de determinación y correlación simples Una prueba F para el modelo 2

Modelo de Regresión Lineal Simple o Supuesto básico: la relación entre la variable dependiente (y) y la variable independiente (x) es aproximadamente una linea recta. 3

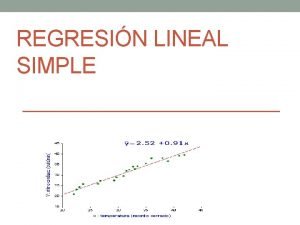
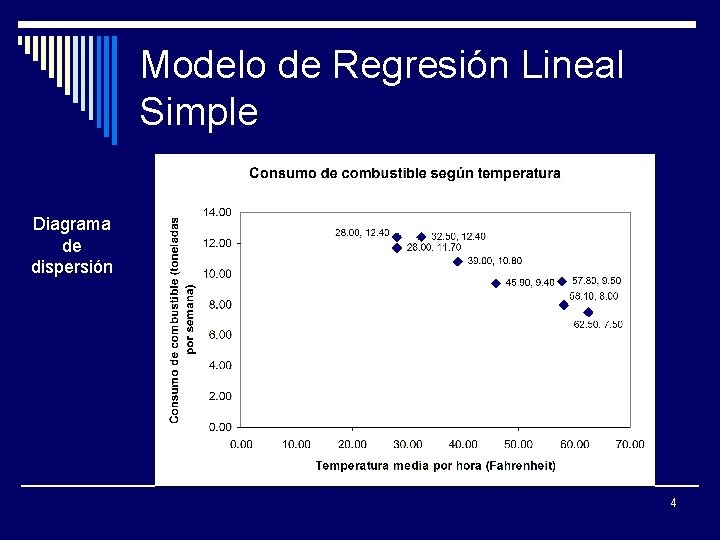
Modelo de Regresión Lineal Simple Diagrama de dispersión 4

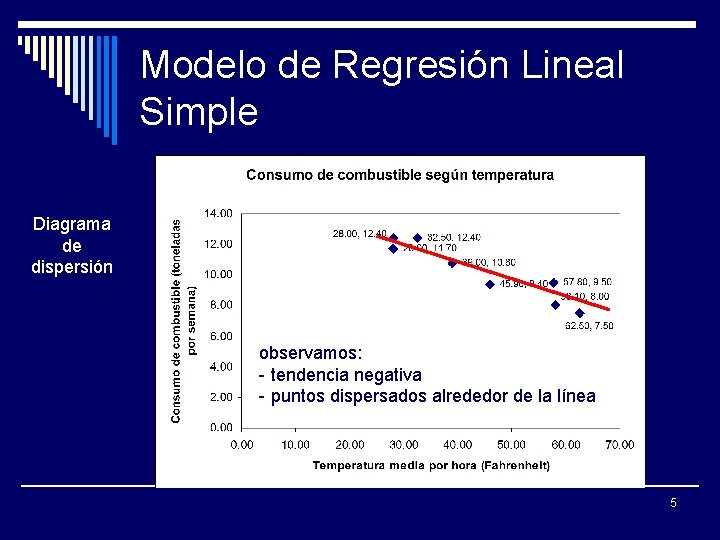
Modelo de Regresión Lineal Simple Diagrama de dispersión observamos: - tendencia negativa - puntos dispersados alrededor de la línea 5

Modelo de Regresión Lineal Simple y = μy|x + = β 0 + β 1 x + o Donde n μy|x = β 0 + β 1 x es el valor medio de la variable dependiente y cuando el valor de la variable independiente es x. n β 0 = ordenada al origen (valor medio de y cuando x = 0) n β 1 = pendiente ( valor medio de y cuando x una unidad) n es un término de error: describe los efectos de todos los factores no incluidos en el modelo 6

Modelo de Regresión Lineal Simple β 0 = 15. 77 y β 1 = -0. 1281, entonces cuando la temperatura x = 28, el valor medio de consumo de combustible que observamos es o Si μy|x = β 0 + β 1 x = 15. 77 – 0. 1281(28) = 12. 1832 MMcf de gas natural. 7

Modelo de Regresión Lineal Simple β 0 = 15. 77 y β 1 = -0. 1281, entonces cuando la temperatura x = 29, el valor medio de consumo de combustible que observamos es o Si μy|x = β 0 + β 1 x = 15. 77 – 0. 1281(29) = 12. 0551 MMcf de gas natural. La diferencia = 12. 0551 - 12. 1832 = -0. 1281 8

Modelo de Regresión Lineal Simple o β 0 y β 1 se llaman parámetros de regresión. o Ya que no conocemos los valores reales de β 0 y β 1 , debemos estimarlos con los datos de la muestra. o (Nota: la interpretación de β 0 a veces no es aplicable. ) o Importante: observamos que estas variables se mueven juntas, mas no podemos deducir una relación causa-efecto. 9

Estimaciones puntuales de los mínimos cuadrados o estimación puntual de los mínimos cuadrados de la pendiente β 1 10

Estimaciones puntuales y predicciones puntuales o Estimación puntual del valor medio de la variable dependiente cuando el valor de la variable independiente es x 0 o se predice =0 11

Estimaciones puntuales y predicciones puntuales o Se puede demostrar que estas estimaciones puntuales dan un valor de la suma de los residuos cuadráticos (SSE) que es menor que la que se obtiene con cualesquiera otros valores de b 0 y b 1. Se les llaman estimaciones puntuales de los mínimos cuadrados. o la recta se llama recta de regresión de mínimos cuadrados o la ecuación se llama ecuación de prediccción de mínimos cuadrados. 12

Suposiciones del modelo y el error estándar o Suposiciones 1. 2. 3. 4. A cualquier valor dado de x, la media de la población de los valores potenciales del término error es igual a cero. Suposición de la varianza constante. A cualquier valor dado de x, tiene una varianza que no depende del valor de x. Suposición de la normalidad. A cualquier valor dado de x, tiene una distribución normal. Suposición de la independencia. Cualquier valor del término error es estadísticamente independiente de cualquier otro valor de . 13

Suposiciones del modelo y el error estándar o En otras palabras, n n n dado un valor de x, la población de valores potenciales del término de error tiene una distribución normal, con valor medio 0 y varianza σ2 que no depende de x. La población de valores potenciales de y|x tiene distribución normal con valor medio de β 0 + β 1 x y varianza σ2 que no depende de x. Es más probable que la suposición de independencia se viole cuando se utilizan series temporales en un estudio de regresión. 14

Suposiciones del modelo y el error estándar o Error cuadrático medio = estimación puntual de σ2 vary|x o error estándar = estimación puntual de σ 15

Prueba de la significancia de la pendiente y la ordenada al origen o Hipótesis nula: β 1 = 0 o nivel de significancia α (0. 10, 0. 05, 0. 01) o los valores p se basan en n-2 grados de libertad o Se rechaza la hipótesis nula si se cumple la condición de punto de rechazo de alguna de las hipótesis alternativas, o si p<α 16

Prueba de la significancia de la pendiente y la ordenada al origen o Si se cumplen los supuestos de la regresión, entonces la población de todos los valores posibles de b 1 es normalmente distribuida con valor medio β 1 y desviación estándar o cuya estimación puntual es 17

Prueba de la significancia de la pendiente y la ordenada al origen o y la población de todos los valores posibles de la estadística de prueba t o tiene una distribución t con n – 2 grados de libertad. 18

Prueba de la significancia de la pendiente y la ordenada al origen Hipótesis alternativa Condición de punto de rechazo Valor p Ha : β 1 ≠ 0 2 (área bajo la curva t a la derecha de |t|) Ha : β 1 > 0 área bajo la curva t a la derecha de t Ha : β 1 < 0 área bajo la curva t a la izquierda de t 19

Intervalos de confianza y de predicción o Si se cumplen las suposiciones de la regresión, un intervalo de confianza de 100(1 -α)% para la pendiente verdadera β 1 es 20

Intervalos de confianza y de predicción o Si se cumplen las suposiciones de la regresión, un valor de distancia (v. d. ) para un valor particular x 0 de x (para la regresión lineal simple) es 21

Intervalos de confianza y de predicción o Si se cumplen las suposiciones de la regresión, un intervalo de confianza de 100(1 -α)% para el valor medio de y cuando la variable independiente es x 0 es 22

Intervalos de confianza y de predicción o La población de todos los errores posibles de predicción está normalmente distribuida con media cero y desviación estándar σ√ 1 + valor de distancia o La estimación puntual es s√ 1 + valor de distancia Se llama error estándar del error de predicción 23

Intervalos de confianza y de predicción o Si se cumplen las suposiciones de la regresión, un intervalo de predicción 100(1 -α)% para un valor individual de y cuando la variable independiente es x 0 es 24

Intervalos de confianza y de predicción o Nótese que el intervalo de predicción es mayor que el intervalo de confianza: mayor incertidumbre acerca del término de error. o Entre más alejado del valor medio es xi, mayores son los intervalos de confianza y de predicción. 25

Coeficientes de determinación y correlación simples o 1. 2. 3. 4. 5. 6. En el caso del modelo de regresión lineal simple, Variación total = Σ(yi-y)2 Variación explicada = Σ(yi-y)2 Variación inexplicada = Σ(yi-yi)2 Variación total = Variación explicada + Variación inexplicada El coeficiente de determinación simple es r 2 = (variación explicada)/(variación total) El r 2 es la proporción de la variación total en los n valores observados de la variable dependiente que explica el modelo de regresión lineal simple 26

Coeficientes de determinación y correlación simples Coeficiente de correlación simple (r) entre y y x o si b 1 > 0 o si b 1 < 0 o donde b 1 es la pendiente de la recta de mínimos cuadrados que relaciona y con x. Este coeficiente de correlación mide la fuerza de la relación lineal entre y y x. 27

Coeficientes de determinación y correlación simples o También se puede calcular mediante la fórmula 28

Coeficientes de determinación y correlación simples o La correlación de la población de todas las combinaciones posibles de valores observados de x e y se denomina ρ o Para probar la hipótesis nula H 0: ρ = 0, utilizamos la estadística de prueba 29

Una prueba F para el modelo o estadística F global F(modelo) = Variación inexplicada (Variación explicada)/(n-2) o Podemos rechazar H 0: β 1=0 y aceptar Ha: β 1≠ 0 en el nivel de significancia α si se cumple alguna de: o F(modelo)>F[α] o Valor p < α o En el punto F[α] se basa en 1 grado de libertad para el numerador y n-2 grados de libertad para el denominador. 30