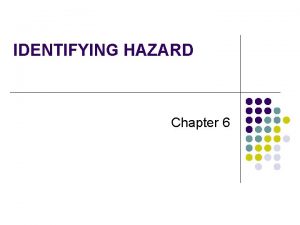
Probabilistic Seismic Hazard Analysis Overview History 1969 Allin
Probabilistic Seismic Hazard Analysis Overview History 1969 - Allin Cornell BSSA paper Rapid development since that time

Probabilistic Seismic Hazard Analysis Overview Deterministic (DSHA) Assumes a single “scenario” Select a single magnitude, M Select a single distance, R Assume effects due to M, R Ground motion parameters Probabilistic (PSHA) Assumes many scenarios Consider all magnitudes Consider all distances Consider all effects Ground motion parameters

Probabilistic Seismic Hazard Analysis Overview Why? Because we don’t know when earthquakes will occur, we don’t know where they will occur, and we don’t know how big they will be Probabilistic (PSHA) Assumes many scenarios Consider all magnitudes Consider all distances Consider all effects Ground motion parameters

Probabilistic Seismic Hazard Analysis Consists of four primary steps: 1. Identification and characterization of all sources 2. Characterization of seismicity of each source 3. Determination of motions from each source 4. Probabilistic calculations PSHA characterizes uncertainty in location, size, frequency, and effects of earthquakes, and combines all of them to compute probabilities of different levels of ground shaking
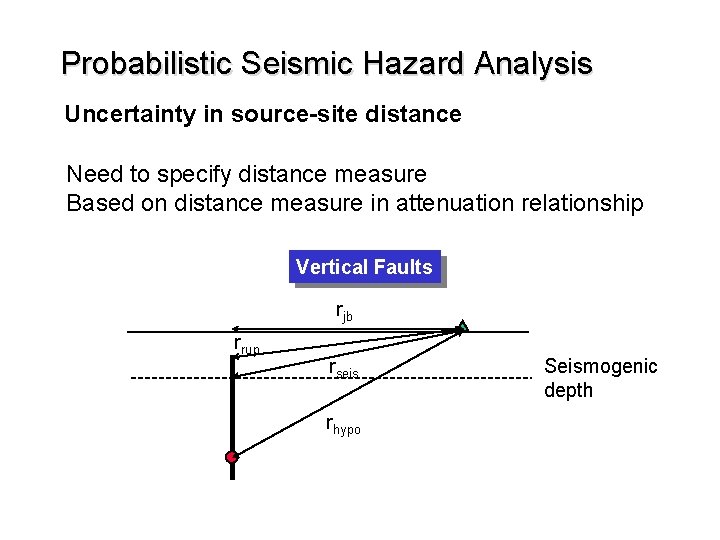
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Need to specify distance measure Based on distance measure in attenuation relationship Vertical Faults rjb rrup rseis rhypo Seismogenic depth
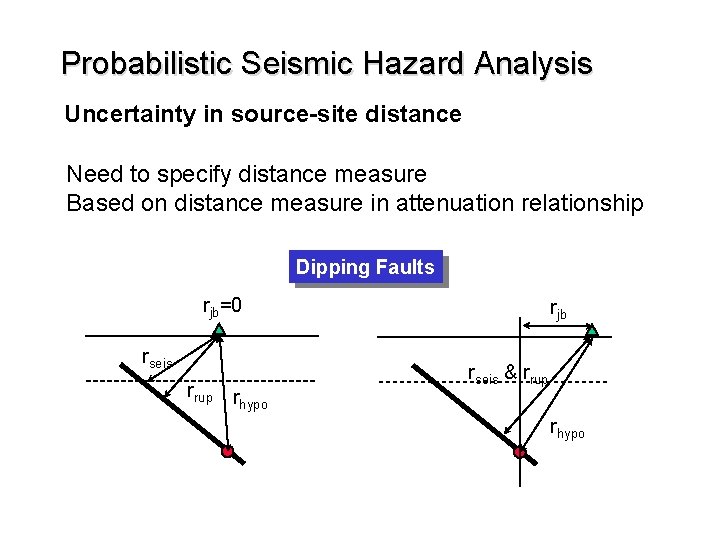
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Need to specify distance measure Based on distance measure in attenuation relationship Dipping Faults rjb=0 rseis rrup r hypo rjb rseis & rrup rhypo
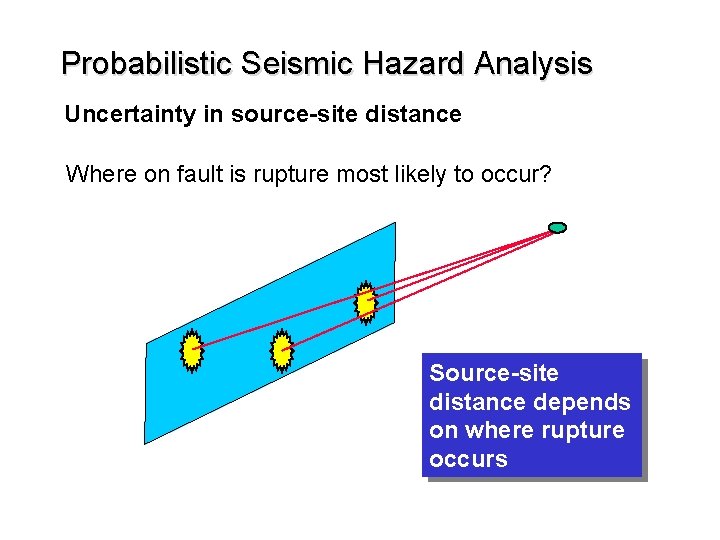
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Where on fault is rupture most likely to occur? Source-site distance depends on where rupture occurs
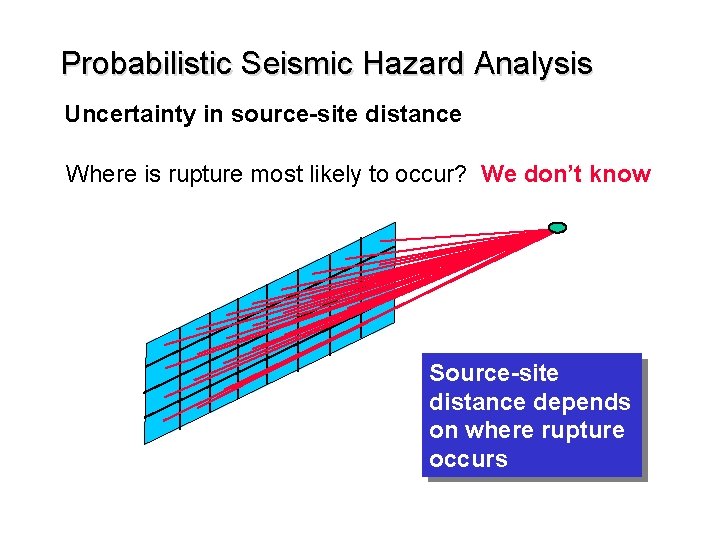
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Where is rupture most likely to occur? We don’t know Source-site distance depends on where rupture occurs
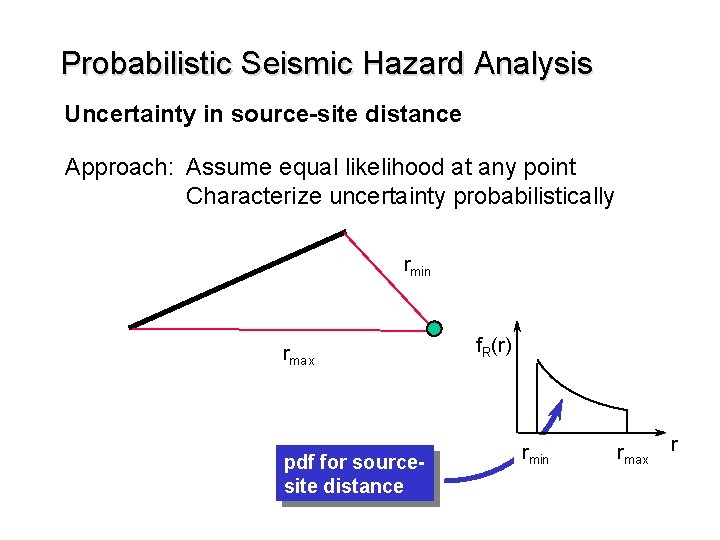
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Approach: Assume equal likelihood at any point Characterize uncertainty probabilistically rmin rmax pdf for sourcesite distance f. R(r) rmin rmax r
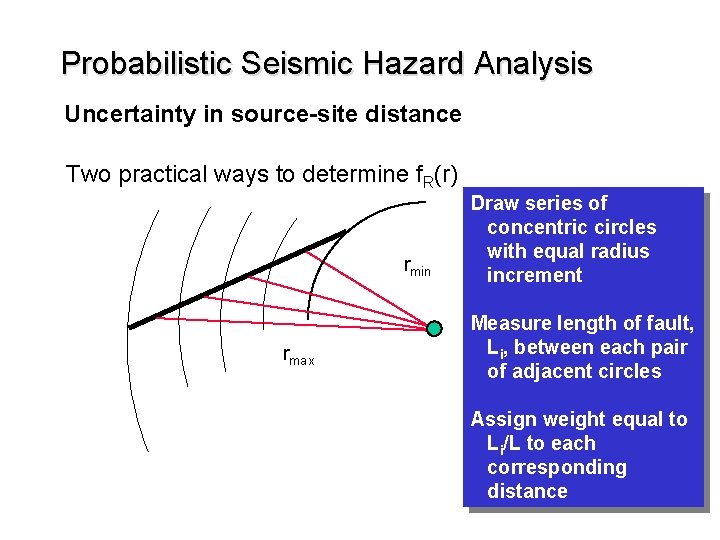
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Two practical ways to determine f. R(r) rmin rmax Draw series of concentric circles with equal radius increment Measure length of fault, Li, between each pair of adjacent circles Assign weight equal to Li/L to each corresponding distance
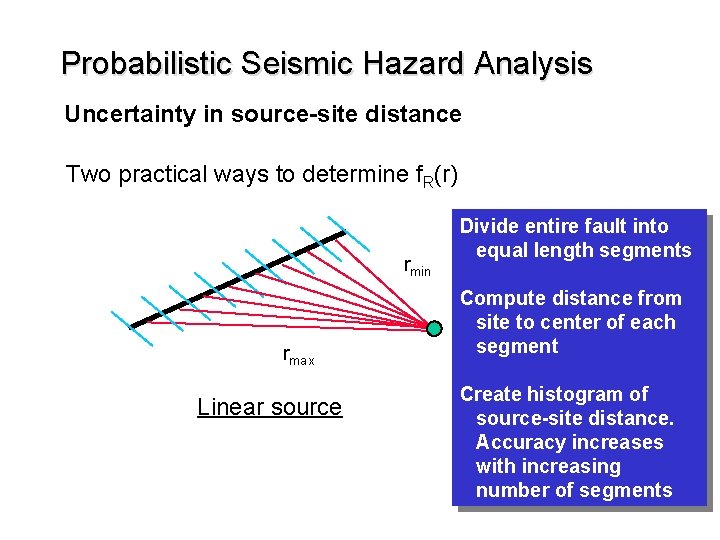
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Two practical ways to determine f. R(r) rmin rmax Linear source Divide entire fault into equal length segments Compute distance from site to center of each segment Create histogram of source-site distance. Accuracy increases with increasing number of segments
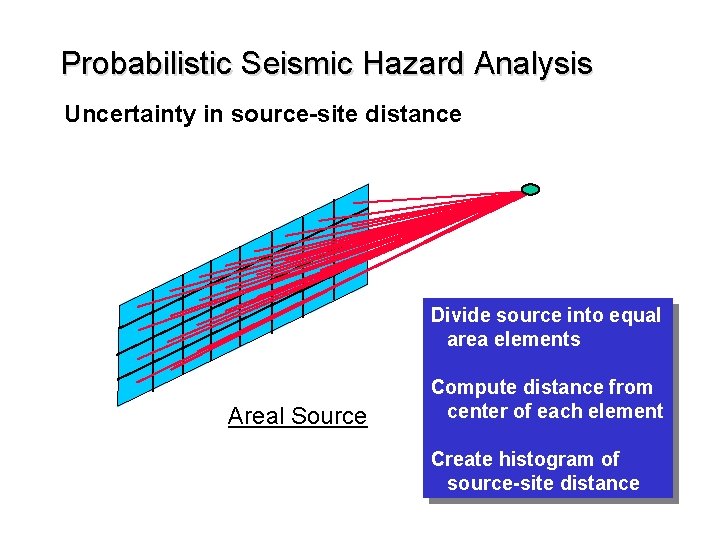
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Divide source into equal area elements Areal Source Compute distance from center of each element Create histogram of source-site distance
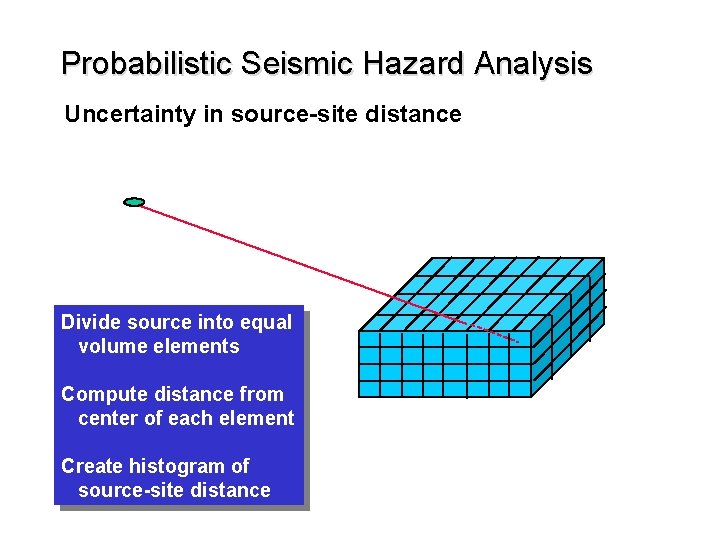
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Divide source into equal volume elements Compute distance from center of each element Create histogram of source-site distance
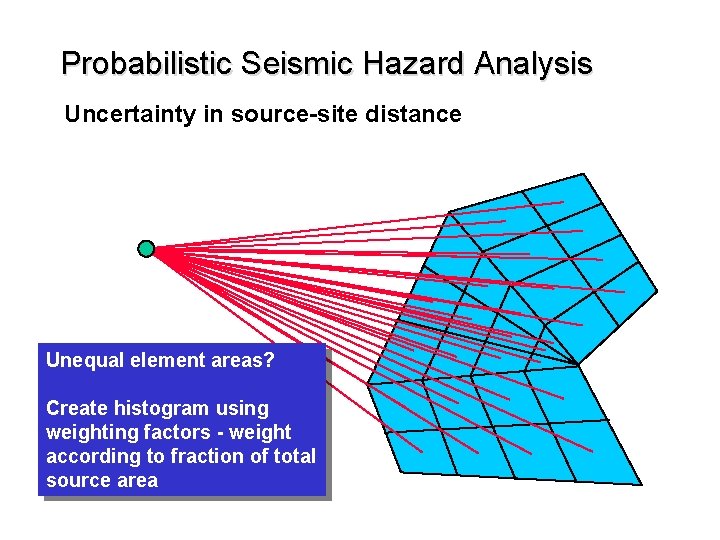
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Unequal element areas? Create histogram using weighting factors - weight according to fraction of total source area
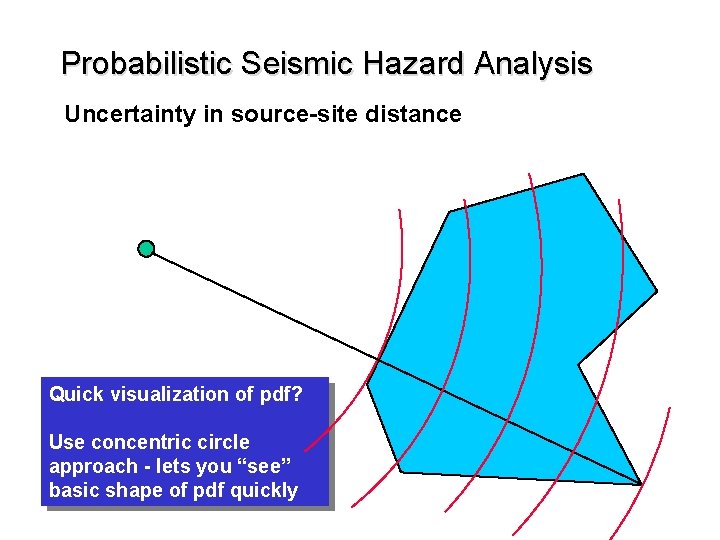
Probabilistic Seismic Hazard Analysis Uncertainty in source-site distance Quick visualization of pdf? Use concentric circle approach - lets you “see” basic shape of pdf quickly

Probabilistic Seismic Hazard Analysis Characterization of maximum magnitude Determination of Mmax - same as for DSHA Empirical correlations Rupture length correlations Rupture area correlations Maximum surface displacement correlations “Theoretical” determination Slip rate correlations Also need to know distribution of magnitudes

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Given source can produce different earthquakes Low magnitude - often Large magnitude - rare Gutenberg-Richter Southern California earthquake data - many faults Counted number of earthquakes exceeding different magnitude levels over period of many years
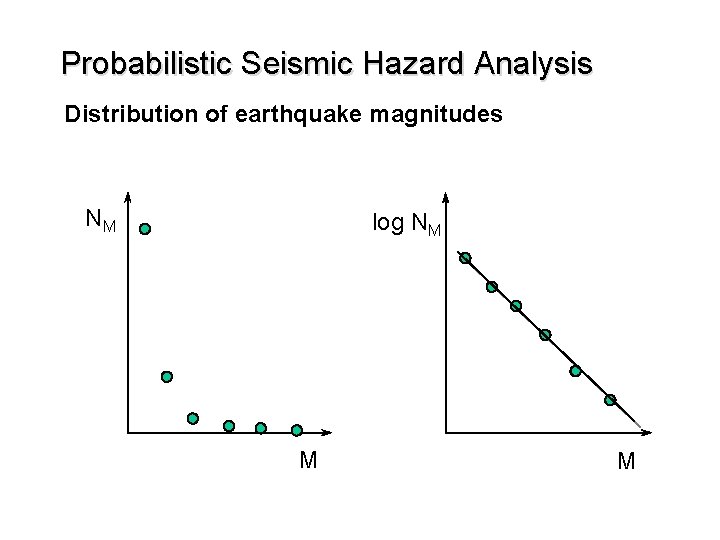
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes NM log NM M M
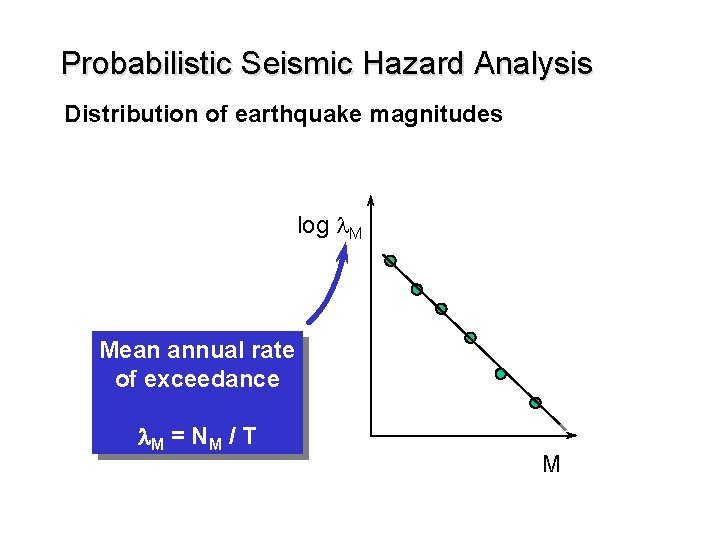
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes log l. M Mean annual rate of exceedance l. M = N M / T M
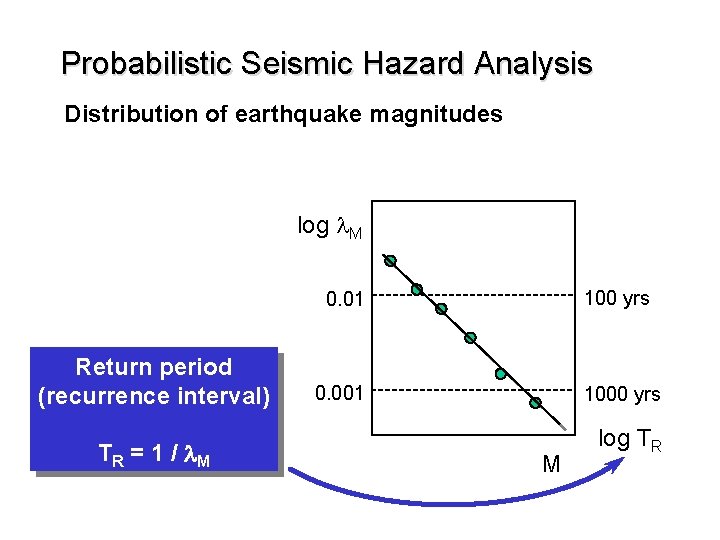
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes log l. M Return period (recurrence interval) TR = 1 / l. M 0. 01 100 yrs 0. 001 1000 yrs M log TR
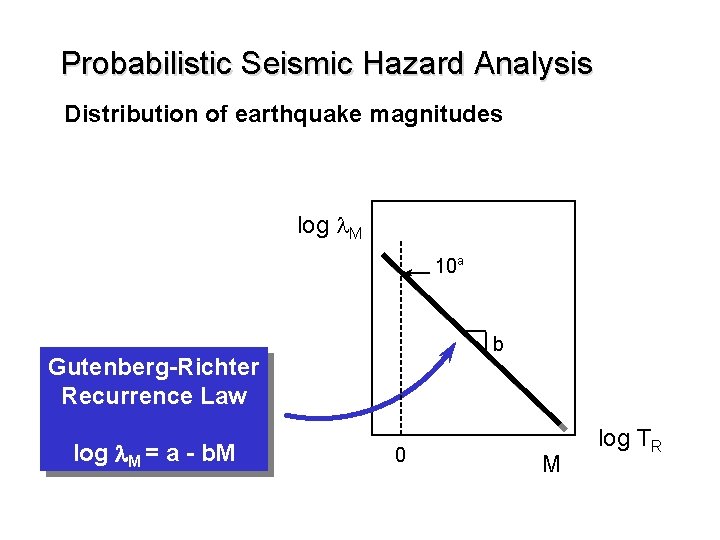
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes log l. M 10 a b Gutenberg-Richter Recurrence Law log l. M = a - b. M 0 M log TR

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Gutenberg-Richter Recurrence Law log l. M = a - b. M Implies that earthquake magnitudes are exponentially distributed (exponential pdf) Can also be written as ln l. M = a - b. M

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Then l. M = 10 a - b. M = exp[a - b. M] where a = 2. 303 a and b = 2. 303 b. For an exponential distribution, f. M(m) = b e-b m

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Neglecting events below minimum magnitude, mo lm = n exp[a - b(m - mo)] where n = exp[a - b mo]. Then, f. M(m) = b e-b (m-mo) m > mo

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes For worldwide data (Circumpacific belt), log lm = 7. 93 - 0. 96 M M=6 lm = 148 /yr TR = 0. 0067 yr M=7 lm = 16. 2 TR = 0. 062 M=8 lm = 1. 78 TR = 0. 562 M = 12 lm = 0. 437 TR = 2. 29 M > 12 every two years?

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Every source has some maximum magnitude Distribution must be modified to account for Mmax Bounded G-R recurrence law
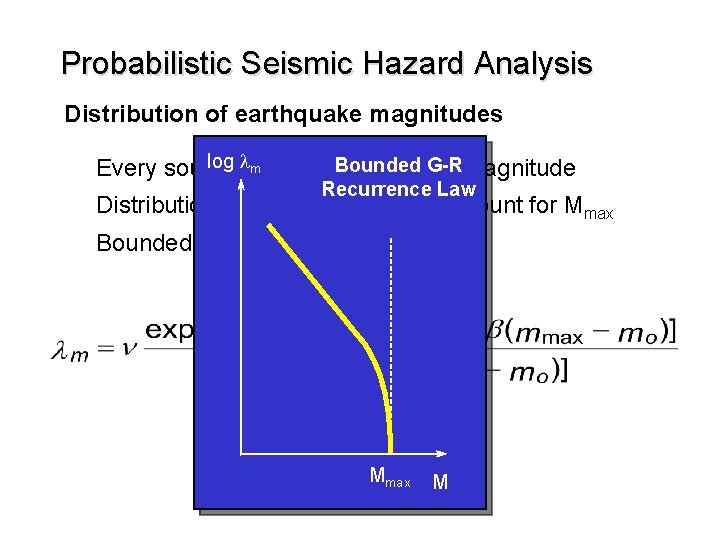
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes log lhas Bounded G-R magnitude m Every source some maximum Recurrence Law Distribution must be modified to account for Mmax Bounded G-R recurrence law Mmax M

Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes Characteristic Earthquake Recurrence Law Paleoseismic investigations Show similar displacements in each earthquake Inividual faults produce characteristic earthquakes Characteristic earthquake occur at or near Mmax Could be caused by geologic constraints More research, field observations needed
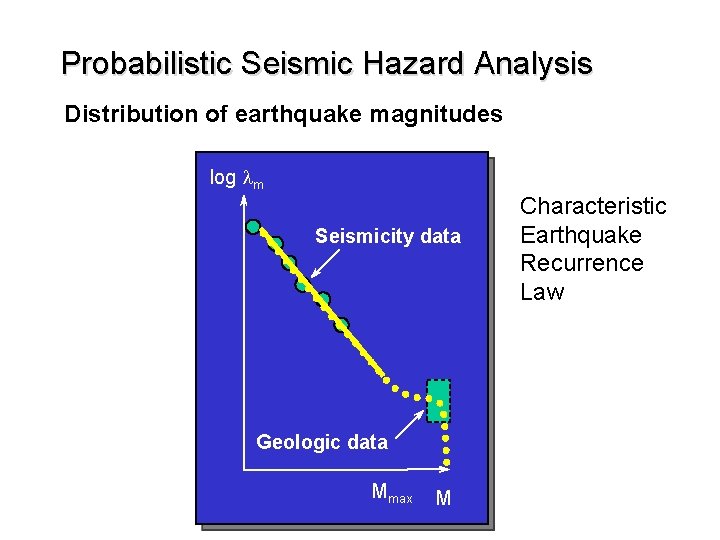
Probabilistic Seismic Hazard Analysis Distribution of earthquake magnitudes log lm Seismicity data Geologic data Mmax M Characteristic Earthquake Recurrence Law
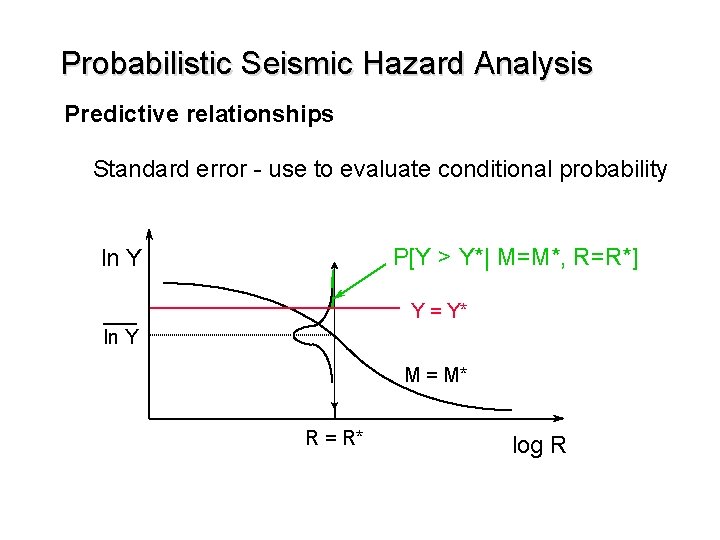
Probabilistic Seismic Hazard Analysis Predictive relationships Standard error - use to evaluate conditional probability log lm P[Y > Y*| M=M*, R=R*] ln Y Y = Y* ln Y M = M* R = R* log R Mmax M
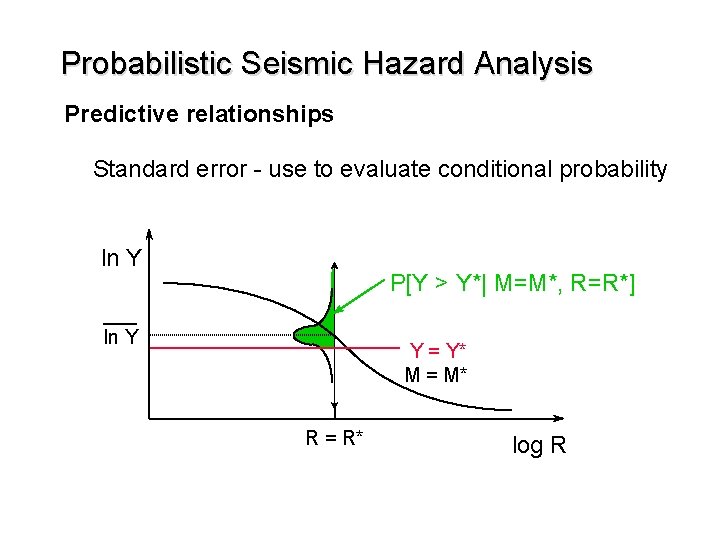
Probabilistic Seismic Hazard Analysis Predictive relationships Standard error - use to evaluate conditional probability ln Y P[Y > Y*| M=M*, R=R*] ln Y Y = Y* M = M* R = R* log R M

Probabilistic Seismic Hazard Analysis Temporal uncertainty Poisson process - describes number of occurrences of an event during a given time interval or spatial region. 1. The number of occurrences in one time interval are independent of the number that occur in any other time interval. 2. Probability of occurrence in a very short time interval is proportional to length of interval. 3. Probability of more than one occurrence in a very short time interval is negligible.

Probabilistic Seismic Hazard Analysis Temporal uncertainty Poisson process where n is the number of occurrences and m is the average number of occurrences in the time interval of interest.

Probabilistic Seismic Hazard Analysis Temporal uncertainty Poisson process Letting m = lt Then

Probabilistic Seismic Hazard Analysis Temporal uncertainty Poisson process Consider an event that occurs, on average, every 1, 000 yrs. What is the probability it will occur at least once in a 100 yr period? l = 1/1000 = 0. 001 P = 1 - exp[-(0. 001)(100)] = 0. 0952

Probabilistic Seismic Hazard Analysis Temporal uncertainty What is the probability it will occur at least once in a 1, 000 yr period? P = 1 - exp[-(0. 001)(1000)] = 0. 632 Solving for l,

Probabilistic Seismic Hazard Analysis Temporal uncertainty Then, the annual rate of exceedance for an event with a 10% probability of exceedance in 50 yrs is The corresponding return period is TR = 1/l = 475 yrs. For 2% in 50 yrs, l = 0. 000404/yr TR = 2475 yrs

Probabilistic Seismic Hazard Analysis Summary of uncertainties Location f. R(r) Source-site distance pdf Size f. M(m) Magnitude pdf Effects P[Y > Y*| M=M*, R=R*] Timing P = 1 - e-lt Poisson model Attenuation relationship including standard error
![Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations U B 1] + P[A Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations U B 1] + P[A](http://slidetodoc.com/presentation_image_h/374ea3c9bd0d94d277c22c688194e4d1/image-39.jpg)
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations U B 1] + P[A B 2] + … + P[A U U P[A] = P[A B N] P[A] = P[A|B 1]P[B 1] + P[A|B 2]P[B 2] + … + P[A|BN]P[BN] B 2 B 1 A B 4 B 3 B 5 Total Probability Theorem

Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations Applying total probability theorem, where X is a vector of parameters. We assume that M and R are the most important parameters and that they are independent. Then,

Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations Above equation gives the probability that y* will be exceeded if an earthquake occurs. Can convert probability to annual rate of exceedance by multiplying probability by annual rate of occurrence of earthquakes. where n = exp[a - bmo]

Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations If the site of interest is subjected to shaking from more than one site (say Ns sites), then For realistic cases, pdfs for M and R are too complicated to integrate analytically. Therefore, we do it numerically.

Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations Dividing the range of possible magnitudes and distances into NM and NR increments, respectively This expression can be written, equivalently, as
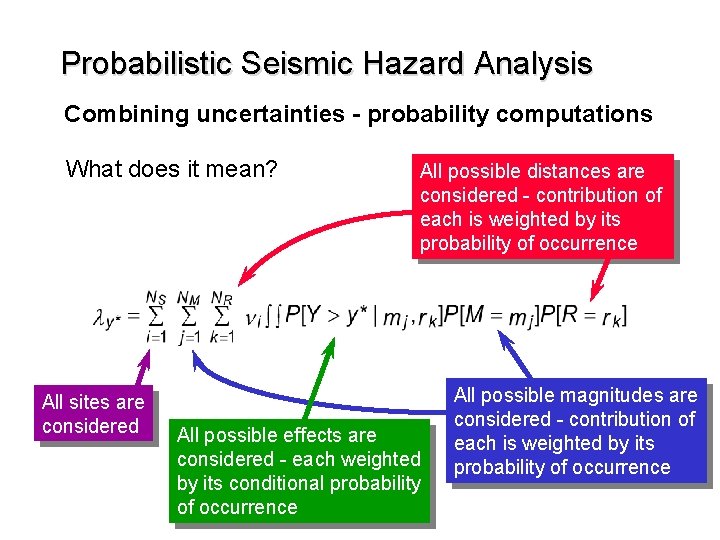
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations What does it mean? All sites are considered All possible distances are considered - contribution of each is weighted by its probability of occurrence All possible effects are considered - each weighted by its conditional probability of occurrence All possible magnitudes are considered - contribution of each is weighted by its probability of occurrence
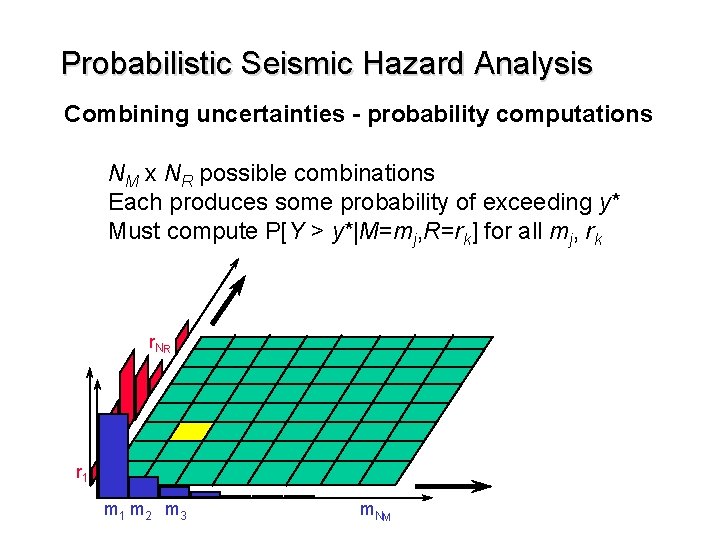
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations NM x NR possible combinations Each produces some probability of exceeding y* Must compute P[Y > y*|M=mj, R=rk] for all mj, rk r. N R r 1 m 2 m 3 m. N M
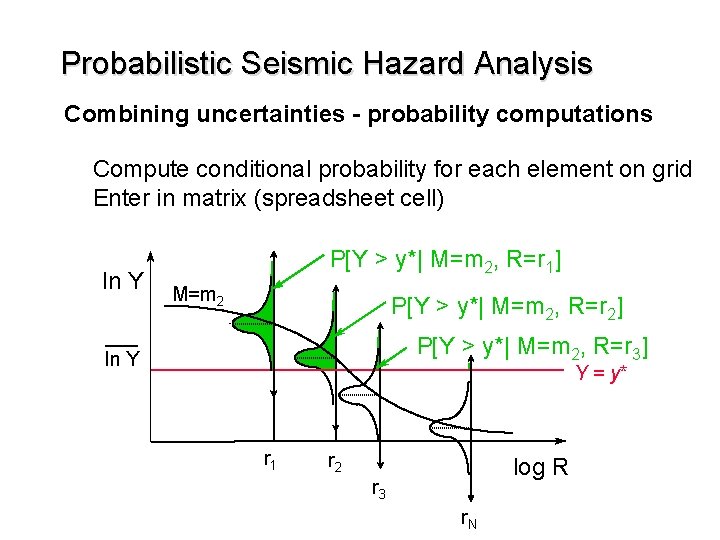
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations Compute conditional probability for each element on grid Enter in matrix (spreadsheet cell) ln Y P[Y > y*| M=m 2, R=r 1] M=m 2 P[Y > y*| M=m 2, R=r 2] P[Y > y*| M=m 2, R=r 3] ln Y Y = y* r 1 r 2 log R r 3 r. N
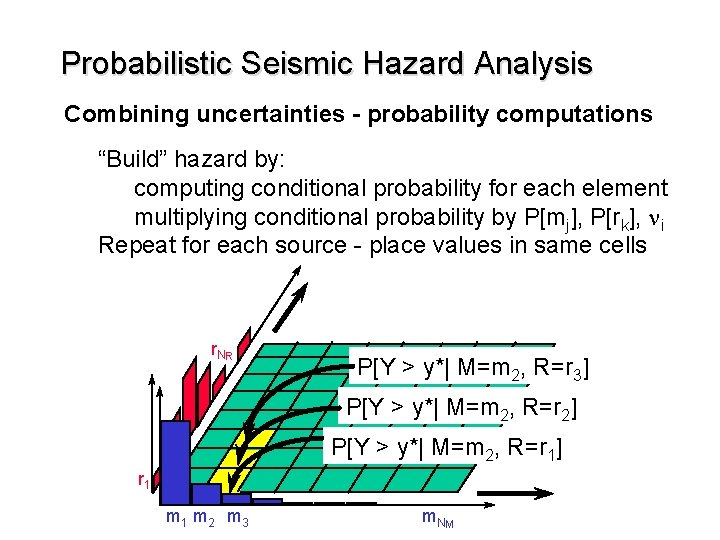
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations “Build” hazard by: computing conditional probability for each element multiplying conditional probability by P[mj], P[rk], ni Repeat for each source - place values in same cells r. N R P[Y > y*| M=m 2, R=r 3] P[Y > y*| M=m 2, R=r 2] P[Y > y*| M=m 2, R=r 1] r 1 m 2 m 3 m. N M
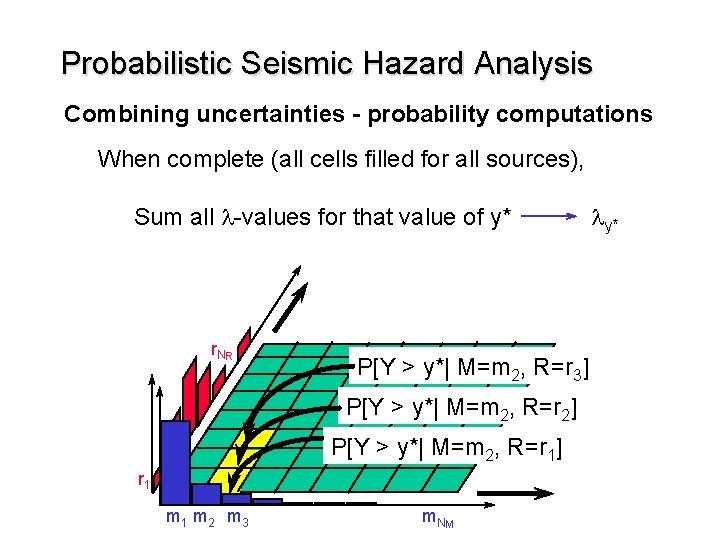
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations When complete (all cells filled for all sources), Sum all l-values for that value of y* r. N R P[Y > y*| M=m 2, R=r 3] P[Y > y*| M=m 2, R=r 2] P[Y > y*| M=m 2, R=r 1] r 1 m 2 m 3 m. N M ly*
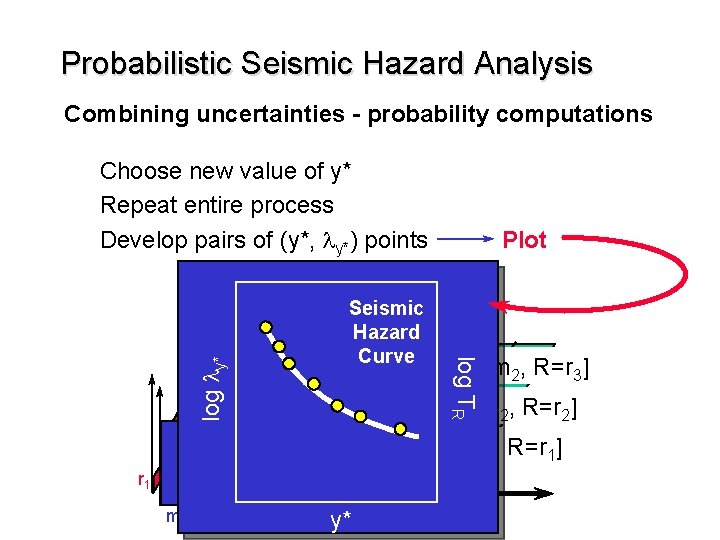
Probabilistic Seismic Hazard Analysis Combining uncertainties - probability computations Choose new value of y* Repeat entire process Develop pairs of (y*, ly*) points log ly* P[Y > y*| M=m 2, R=r 3] log TR r. N R Seismic Hazard Curve Plot P[Y > y*| M=m 2, R=r 2] P[Y > y*| M=m 2, R=r 1] r 1 m 2 m 3 y* m. N M
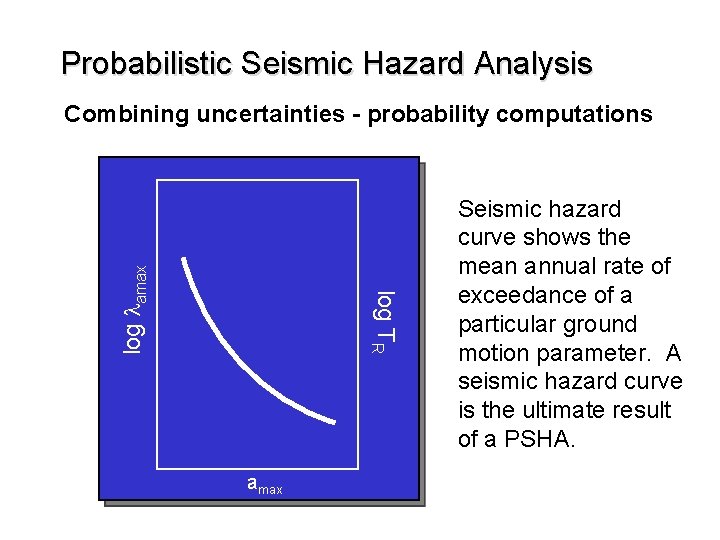
Probabilistic Seismic Hazard Analysis log ly* amax y* Seismic hazard curve shows the mean annual rate of exceedance of a particular ground motion parameter. A seismic hazard curve is the ultimate result of a PSHA. log TR log lamax Combining uncertainties - probability computations
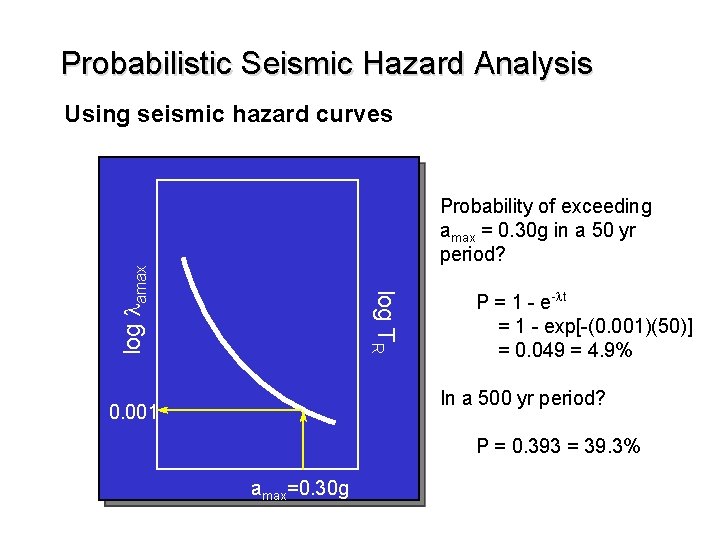
Probabilistic Seismic Hazard Analysis Using seismic hazard curves log TR log lamax Probability of exceeding amax = 0. 30 g in a 50 yr period? P = 1 - e-lt = 1 - exp[-(0. 001)(50)] = 0. 049 = 4. 9% In a 500 yr period? 0. 001 P = 0. 393 = 39. 3% amax=0. 30 g
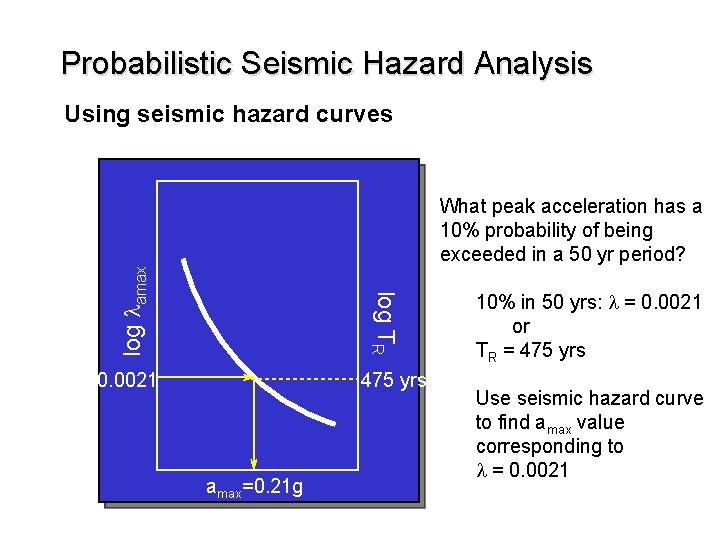
Probabilistic Seismic Hazard Analysis Using seismic hazard curves log TR log lamax What peak acceleration has a 10% probability of being exceeded in a 50 yr period? 0. 0021 475 yrs amax=0. 21 g 10% in 50 yrs: l = 0. 0021 or TR = 475 yrs Use seismic hazard curve to find amax value corresponding to l = 0. 0021
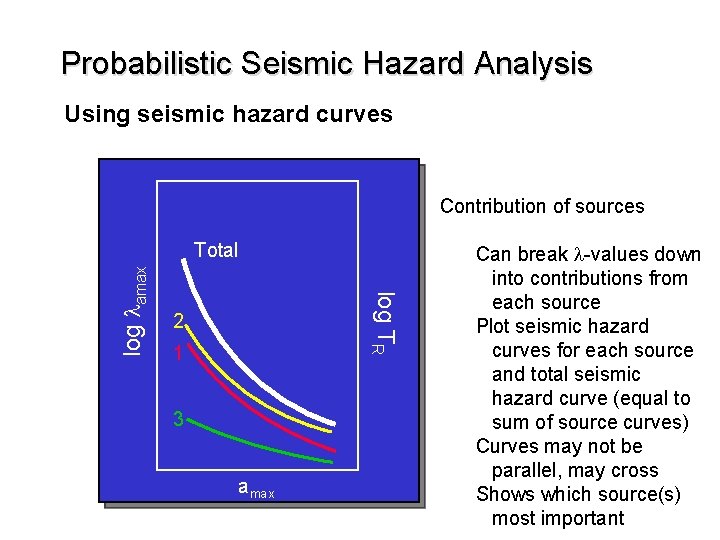
Probabilistic Seismic Hazard Analysis Using seismic hazard curves Contribution of sources log TR log lamax Total 2 1 3 amax Can break l-values down into contributions from each source Plot seismic hazard curves for each source and total seismic hazard curve (equal to sum of source curves) Curves may not be parallel, may cross Shows which source(s) most important
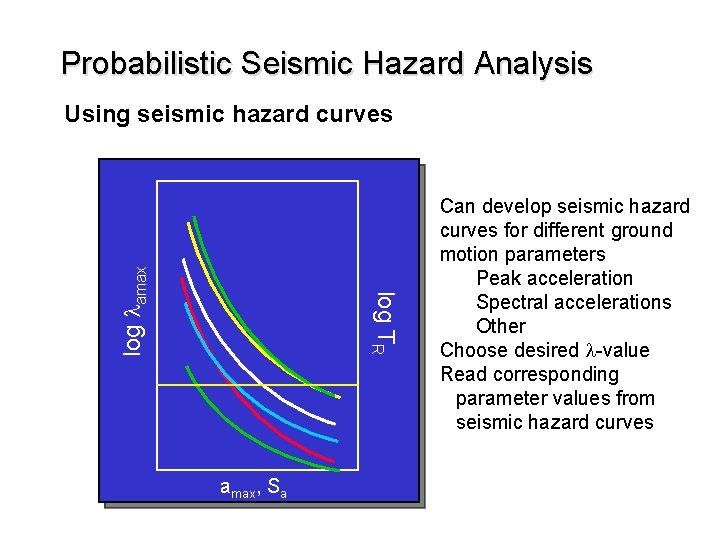
Probabilistic Seismic Hazard Analysis log TR log lamax Using seismic hazard curves amax, Sa Can develop seismic hazard curves for different ground motion parameters Peak acceleration Spectral accelerations Other Choose desired l-value Read corresponding parameter values from seismic hazard curves
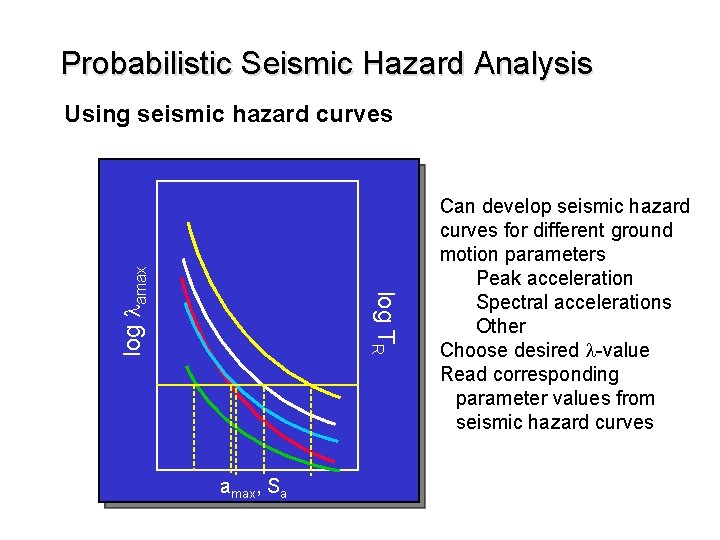
Probabilistic Seismic Hazard Analysis log TR log lamax Using seismic hazard curves amax, Sa Can develop seismic hazard curves for different ground motion parameters Peak acceleration Spectral accelerations Other Choose desired l-value Read corresponding parameter values from seismic hazard curves
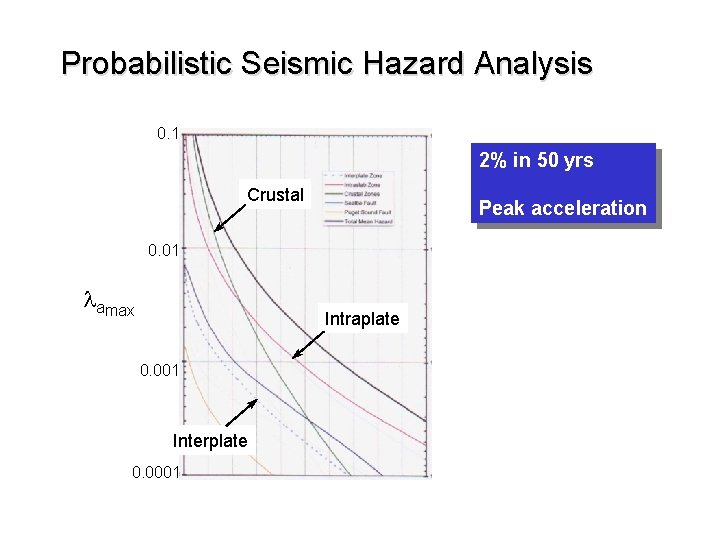
Probabilistic Seismic Hazard Analysis 0. 1 2% in 50 yrs Crustal Peak acceleration 0. 01 lamax Intraplate 0. 001 Interplate 0. 0001
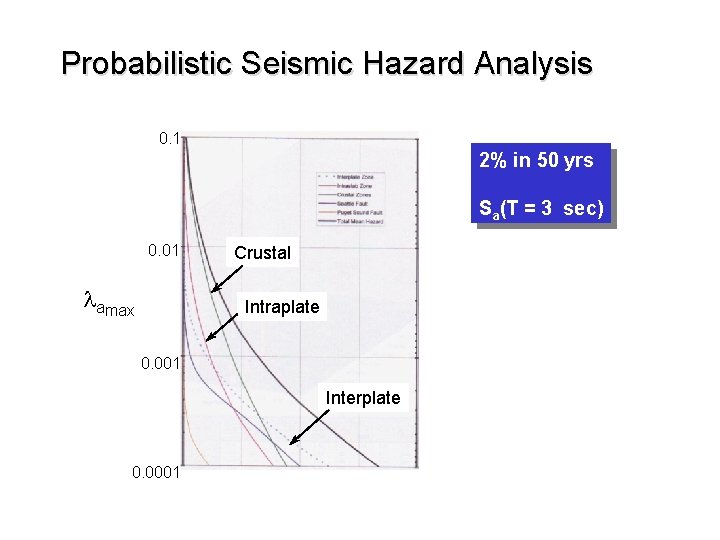
Probabilistic Seismic Hazard Analysis 0. 1 2% in 50 yrs Sa(T = 3 sec) 0. 01 lamax Crustal Intraplate 0. 001 Interplate 0. 0001
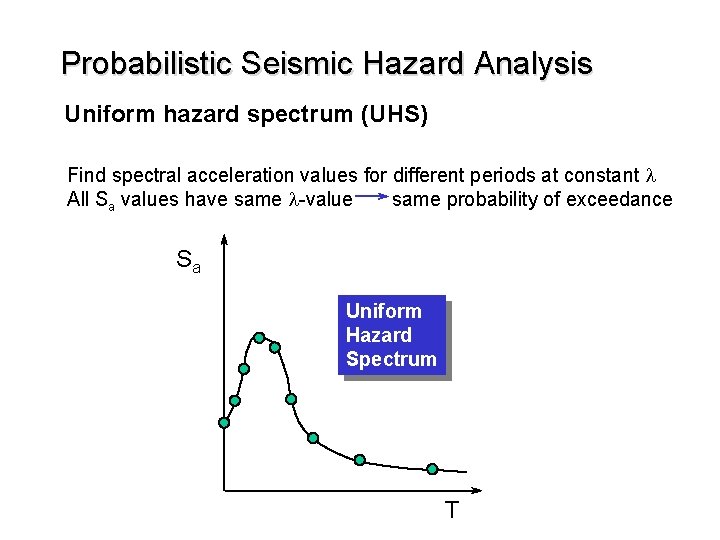
Probabilistic Seismic Hazard Analysis Uniform hazard spectrum (UHS) Find spectral acceleration values for different periods at constant l All Sa values have same l-value same probability of exceedance Sa Uniform Hazard Spectrum T

Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) Common question: What magnitude & distance does that amax value correspond to? 5. 0 5. 5 6. 0 6. 5 7. 0 7. 5 8. 0 8. 5 25 km 0. 01 0. 02 0. 03 0. 02 0. 01 50 km 0. 02 0. 03 0. 04 0. 05 0. 04 0. 03 0. 02 75 km 0. 03 0. 05 0. 06 0. 09 0. 06 0. 05 0. 02 100 km 0. 03 0. 05 0. 08 0. 05 0. 02 125 km 0. 02 0. 03 0. 04 0. 05 0. 03 0. 02 0. 01 150 km 0. 01 0. 02 0. 03 0. 05 0. 02 0. 01 0. 00 175 km 0. 00 0. 01 0. 03 0. 01 0. 00 200 km 0. 00 0. 01 0. 00 Total hazard includes contributions from all combinations of M & R.
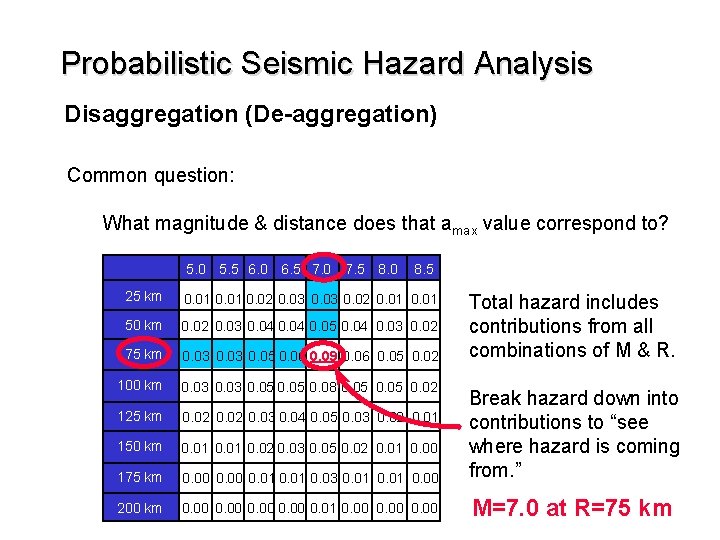
Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) Common question: What magnitude & distance does that amax value correspond to? 5. 0 5. 5 6. 0 6. 5 7. 0 7. 5 8. 0 8. 5 25 km 0. 01 0. 02 0. 03 0. 02 0. 01 50 km 0. 02 0. 03 0. 04 0. 05 0. 04 0. 03 0. 02 75 km 0. 03 0. 05 0. 06 0. 09 0. 06 0. 05 0. 02 100 km 0. 03 0. 05 0. 08 0. 05 0. 02 125 km 0. 02 0. 03 0. 04 0. 05 0. 03 0. 02 0. 01 150 km 0. 01 0. 02 0. 03 0. 05 0. 02 0. 01 0. 00 175 km 0. 00 0. 01 0. 03 0. 01 0. 00 Break hazard down into contributions to “see where hazard is coming from. ” 200 km 0. 00 0. 01 0. 00 M=7. 0 at R=75 km Total hazard includes contributions from all combinations of M & R.
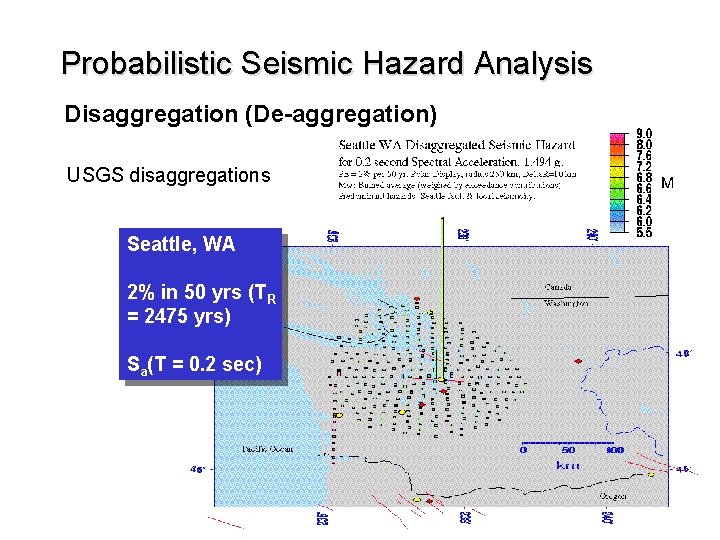
Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) USGS disaggregations Seattle, WA 2% in 50 yrs (TR = 2475 yrs) Sa(T = 0. 2 sec)
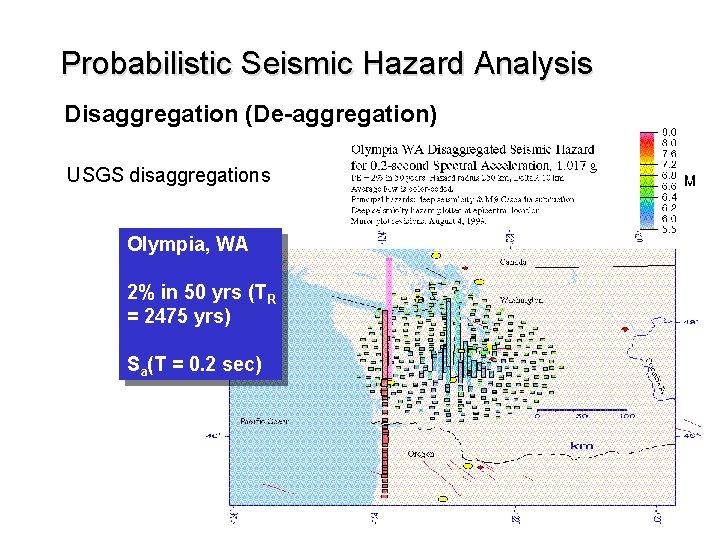
Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) USGS disaggregations Olympia, WA 2% in 50 yrs (TR = 2475 yrs) Sa(T = 0. 2 sec)
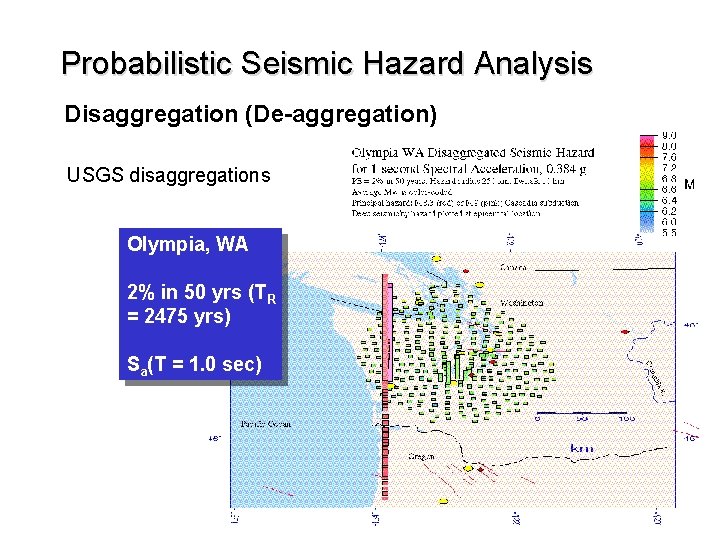
Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) USGS disaggregations Olympia, WA 2% in 50 yrs (TR = 2475 yrs) Sa(T = 1. 0 sec)
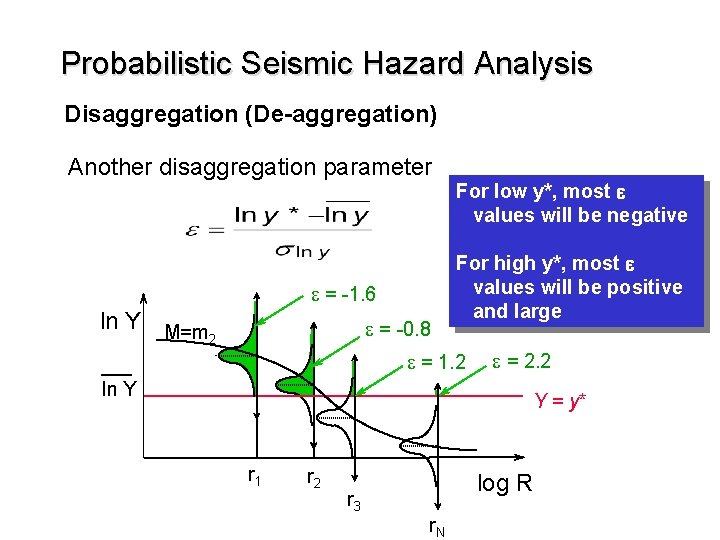
Probabilistic Seismic Hazard Analysis Disaggregation (De-aggregation) Another disaggregation parameter e = -1. 6 ln Y M=m 2 e = -0. 8 For low y*, most e values will be negative For high y*, most e values will be positive and large e = 1. 2 e = 2. 2 ln Y Y = y* r 1 r 2 r 3 log R r. N

Probabilistic Seismic Hazard Analysis Logic tree methods Not all uncertainty can be described by probability distributions Most appropriate model may not be clear • Attenuation relationship • Magnitude distribution • etc. Experts may disagree on model parameters • Fault segmentation • Maximum magnitude • etc.
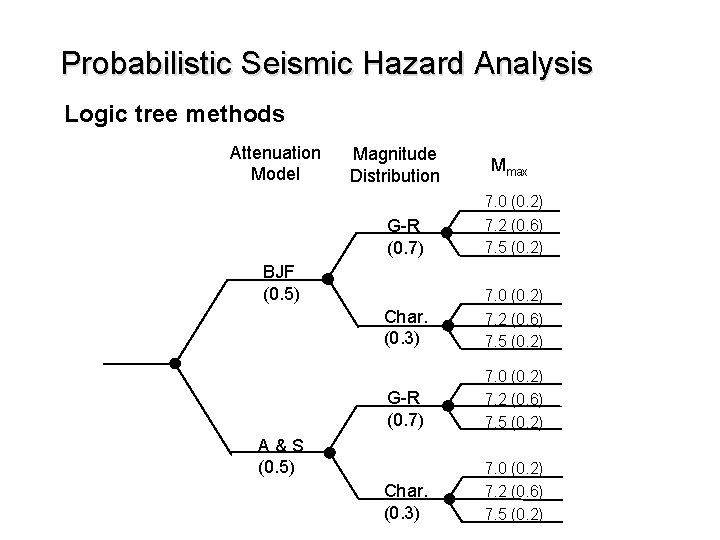
Probabilistic Seismic Hazard Analysis Logic tree methods Attenuation Model Magnitude Distribution Mmax G-R (0. 7) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) Char. (0. 3) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) BJF (0. 5) A&S (0. 5)
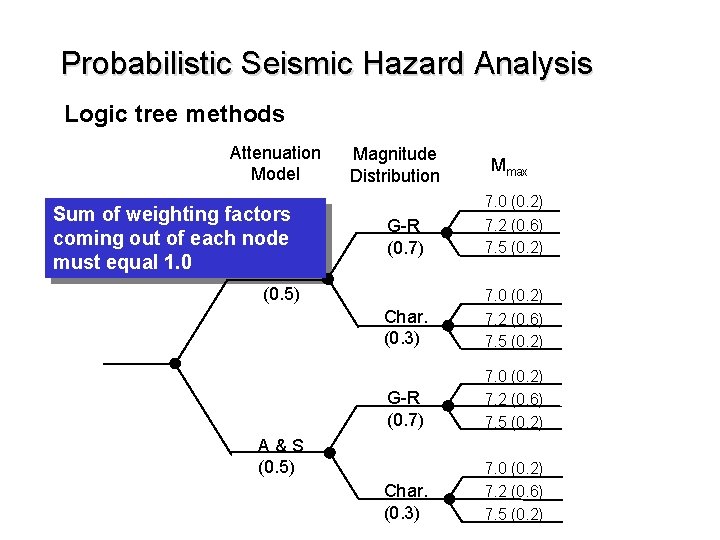
Probabilistic Seismic Hazard Analysis Logic tree methods Attenuation Model Sum of weighting factors coming out of each node must equal 1. 0 BJF Magnitude Distribution Mmax G-R (0. 7) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) Char. (0. 3) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) (0. 5) A&S (0. 5)
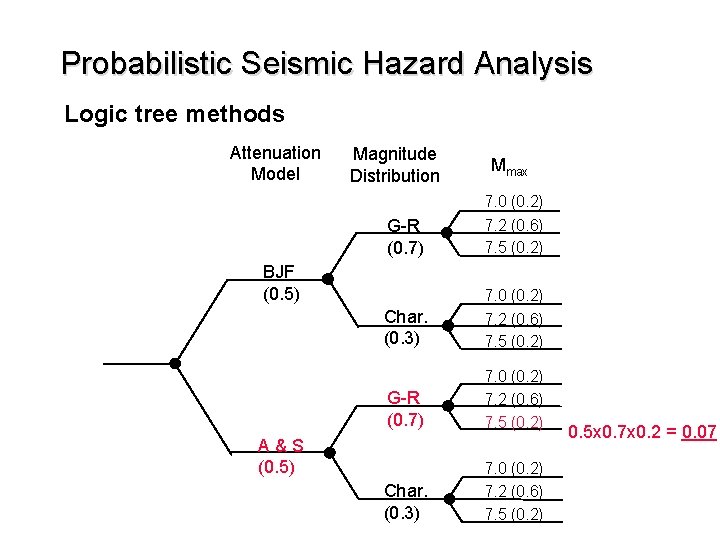
Probabilistic Seismic Hazard Analysis Logic tree methods Attenuation Model Magnitude Distribution Mmax G-R (0. 7) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) Char. (0. 3) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) BJF (0. 5) A&S (0. 5) 0. 5 x 0. 7 x 0. 2 = 0. 07
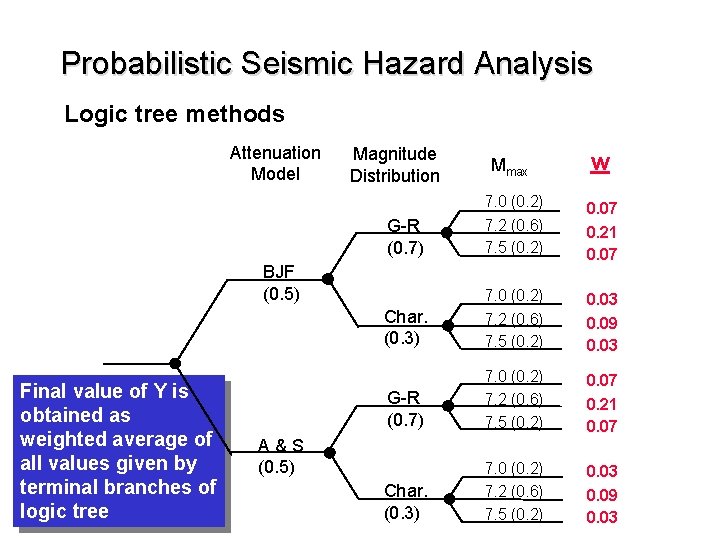
Probabilistic Seismic Hazard Analysis Logic tree methods Attenuation Model Magnitude Distribution Mmax w G-R (0. 7) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) 0. 07 0. 21 0. 07 Char. (0. 3) 7. 0 (0. 2) 7. 2 (0. 6) 7. 5 (0. 2) 0. 03 0. 09 0. 03 BJF (0. 5) Final value of Y is obtained as weighted average of all values given by terminal branches of logic tree A&S (0. 5)

Probabilistic Seismic Hazard Analysis Logic tree methods Recent PSHA logic tree included: Cascadia interplate 2 attenuation relationships 2 updip boundaries 3 downdip boundaries 2 return periods 4 segmentation models 2 maximum magnitude approaches 192 terminal branches

Probabilistic Seismic Hazard Analysis Logic tree methods Recent PSHA logic tree included: Cascadia intraplate 2 intraslab geometries 3 maximum magnitudes 2 a-values 2 b-values 24 terminal branches

Probabilistic Seismic Hazard Analysis Logic tree methods Recent PSHA logic tree included: Seattle Fault and Puget Sound Fault 2 attenuation relationships 3 activity states 3 maximum magnitudes 2 recurrence models 2 slip rates 72 terminal branches for Seattle Fault 72 terminal branches for Puget Sound Fault

Probabilistic Seismic Hazard Analysis Logic tree methods Recent PSHA logic tree included: Crustal areal source zones 7 source zones 2 attenuation relationships 3 maximum magnitudes 2 recurrence models 3 source depths 252 terminal branches Total PSHA required analysis of 612 combinations
- Slides: 73