Private Information Retrieval Yuval Ishai Computer Science Department

Private Information Retrieval Yuval Ishai Computer Science Department Technion

Talk Overview • Intro to PIR – Motivation and problem definition – Toy examples – State of the art • Relation with other primitives – Locally Decodable Codes – (Oblivious Transfer, CRHF) • Constructions • Open problems

Private Information Retrieval (PIR) [CGKS 95] • Goal: allow a user to access a database while hiding what she is after. • Motivation: patent databases, web searches, etc. • Paradox(? ) : imagine buying in a store without the seller knowing what you buy. Note: Encrypting requests is useful against third parties; not against server holding the data.

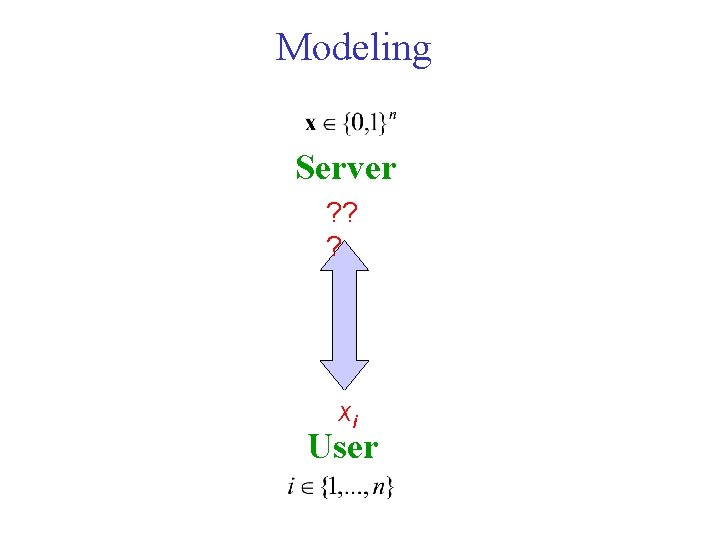
Modeling Server ? ? ? xi User

Some “solutions” 1. User downloads entire database. Drawback: n communication bits (vs. logn+1 w/o privacy). Main research goal: minimize communication complexity. 2. User masks i with additional random indices. Drawback: gives a lot of information about i. 3. Enable anonymous access to database. Addresses a different concern: hides identity of user, not the fact that xi is retrieved. Fact: PIR as described so far requires (n) communication bits.

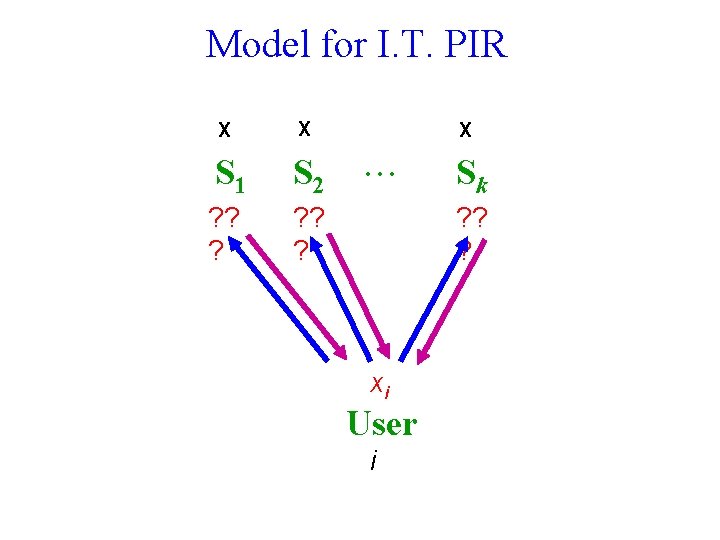
Two Approaches Computational PIR [KO 97, CMS 99, . . . ] Computational privacy, based on cryptographic assumptions. Information-Theoretic PIR [CGKS 95, Amb 97, . . . ] Replicate database among k servers. Unconditional privacy against t servers. Default: t=1

Model for I. T. PIR X X S 1 S 2 ? ? ? X Sk ? ? ? xi User i

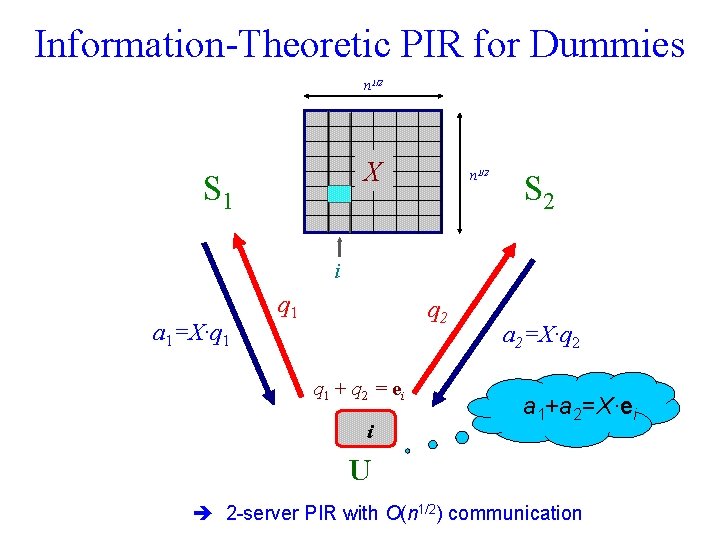
Information-Theoretic PIR for Dummies n 1/2 X S 1 n 1/2 S 2 i a 1=X·q 1 q 2 q 1 + q 2 = ei i a 2=X·q 2 a 1+a 2=X·ei U 2 -server PIR with O(n 1/2) communication

Computational PIR for Dummies Tool: homomorphic encryption a b Protocol: = a+b • User sends E(ei) E(0) E(1) E(0) (=c 1 c 2 c 3 c 4) X= n 1/2 0110 1 1 1 0 n 1/2 1100 0001 • Server replies with E(X·ei) c 2 c 3 c 1 c 2 c 4 • User recovers ith column of X i PIR with ~ O(n 1/2) communication

Bounds for Computational PIR servers comm. assumption [CG 97] 2 O(n ) [KO 97] 1 O(n ) one-way function homomorphic QRA / encryption [CMS 99] 1 polylog(n) -hiding … DCRA [Lipmaa] [KO 00] 1 n-o(n) trapdoor permutation

Bounds for I. T. PIR Upper bounds: – O(log n / loglog n) servers, polylog(n) [BF 90, BFKR 91, CGKS 95] – 2 servers, O(n 1/3); k servers, O(n 1/k) [CGKS 95] – k servers, O(n 1/(2 k-1)) [Amb 97, Ito 99, IK 99, BI 01, WY 05] • t-private, O(nt/(2 k-1)) [BI 01, WY 05] – k servers, O(ncloglogk /(klogk)) [BIKR 02]. BIKR “dirty” AMB CGKS “clean” inefficient IK BI WY efficient Lower bounds: – log n +1 (no privacy) – 2 servers, ~5 log n ; k servers, ck log n – Better for restricted 2 -server protocols [Man 98, Wd. W 04] [CGKS 95, GKST 02, BFG 02, Kd. W 03, Wd. W 04]

Why Information-Theoretic PIR? Cons: • Requires multiple servers • Privacy against limited collusions • Worse asymptotic complexity (with const. k): O(nc) vs. polylog(n) Pros: • • • Neat question Unconditional privacy Better “real-life” efficiency Allows very short queries or very short answers (+apps [DIO 98, BIM 99] ) Closely related to a natural coding problem [KT 00]

Locally Decodable Codes [KT 00] x y i Requirements: • High fault-tolerance • Local decoding Recover from m faults… … with ½+ probability Question: how large should m(n) be in a k-query LDC? k=2: 2 (n) k=3: 2 O(n^ 0. 5) (n 2)

From I. T. PIR to LDC k-server PIR with -bit queries and -bit answers k-query LDC of length 2 over ={0, 1} y[q]=Answer(x, q) • Converse relation also holds. • Binary LDC PIR with one answer bit per server • Best known LDC are obtained from PIR protocols. – const. q: m=exp(nc loglogq / qlogq)

A Question about MPC Ben-Or, Goldwasser, Wigderson, 1988 Chaum, Crépeau, Damgård, 1988 Information-theoretic MPC is feasible! Beaver, Micali, Rogaway, 1990 B. , Feigenbaum, Kilian, R. , 1990 Open question: k 3 players can compute any function f of their inputs with total work = poly(circuit-size) Can k computationally unbounded players compute an arbitrary f with communication = poly(input-length)? … or with work = poly(formula-size) and constant rounds [BB 89, …] Can this be done using a constant number of rounds?

Question Reformulated Is the communication complexity of MPC strongly correlated with the computational complexity of the function being computed? All functions efficiently computable functions = communication-efficient MPC = no communication-efficient MPC

Connecting MPC and LDC [IK 04] 1990 [KT 00] 1995 2000 • The three problems are “essentially equivalent” – up to considerable deterioration of parameters

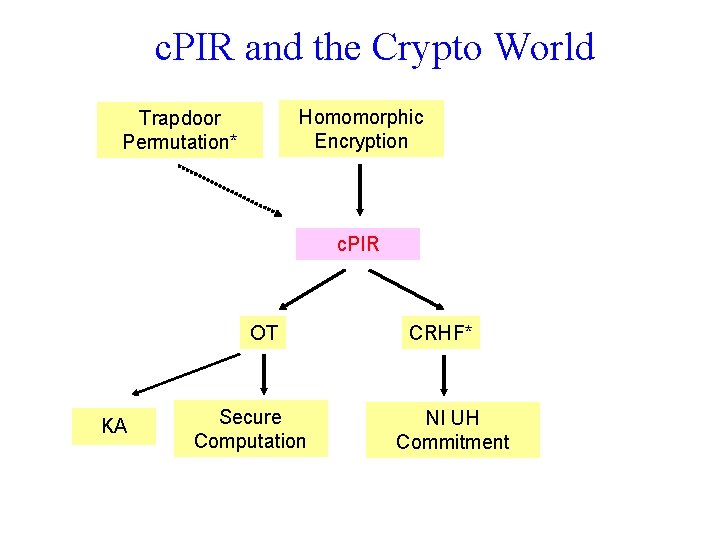
c. PIR and the Crypto World Homomorphic Encryption Trapdoor Permutation* c. PIR OT KA Secure Computation CRHF* NI UH Commitment

PIR as a Building Block • Private storage [OS 98] • Sublinear-communication secure computation – – – 1 -out-of-n Oblivious Transfer (SPIR) [GIKM 98, NP 99, …] Keyword search [CGN 99, FIPR 05] Statistical queries ]CIKRRW 01[ Approximate distance ]FIMNSW 01, IW 04[ Communication-preserving secure function evaluation [NN 01]

Time Complexity of PIR Focus so far: communication complexity Obstacle: time complexity • Server/s must spend at least linear time. Workarounds: • Preprocessing [BIM 00] • Amortization [BIM 00, IKOS 04] Non-adaptive Adaptive Single user ? Multiple users ? ?

Protocols

• High level structure of all known protocols – User maps i into a point z Fm – User secret-shares z between servers using some t-threshold LSSS over F – Server j responds with a linear function of x determined by its share of z. • Two types of protocols: – Polynomial-based [BF 90, BFKR 91, CGKS 95, …, WY 05] • LSSS = Shamir • Scale well with k, t – Replication-based • • [IK 99, BI 01, BIKR 02] LSSS = CNF Do not scale well with k, t - involve (k choose t) replication overhead However, dominate over polynomial-based up to (k choose t) factor [CDI 05] Best known protocols for constant k

Polynomial-Based Protocols • Step 1: Arithmetization – Fix a degree parameter d (will be determined by k) • Goal: Communication = O(n 1/d) – User maps i [n] into a weight-d vector z of length m=O(n 1/d). • 1 11100…. 0 2 11010… 0 n 00… 0111 – Servers view x as a degree-d m-variate polynomial P(Z 1, …, Zm)= x 1 Z 1 Z 2 Z 3 + x 2 Z 1 Z 2 Z 4 + … + xn. Zm-2 Zm-1 Zm – Privately retrieving i-th bit of x privately evaluating P on z.

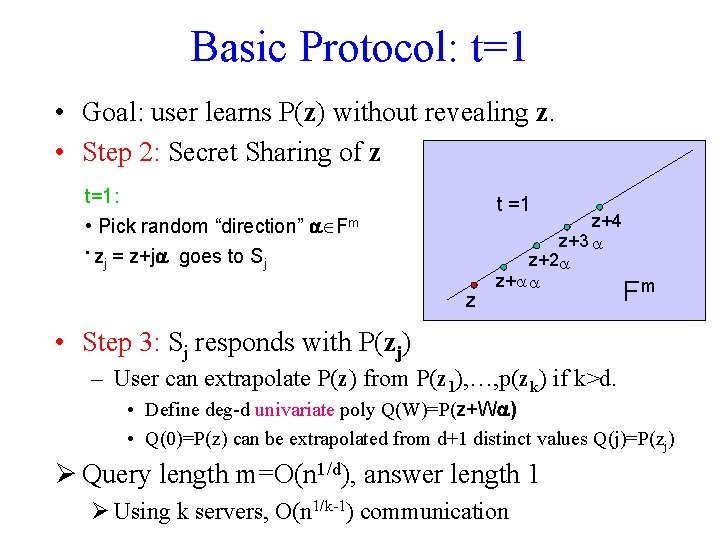
Basic Protocol: t=1 • Goal: user learns P(z) without revealing z. • Step 2: Secret Sharing of z t=1: • Pick random “direction” Fm • z = z+j goes to S j j t =1 z z+4 z+3 z+2 z+ Fm • Step 3: Sj responds with P(zj) – User can extrapolate P(z) from P(z 1), …, p(zk) if k>d. • Define deg-d univariate poly Q(W)=P(z+W ) • Q(0)=P(z) can be extrapolated from d+1 distinct values Q(j)=P(zj) Ø Query length m=O(n 1/d), answer length 1 Ø Using k servers, O(n 1/k-1) communication

Basic Protocol: General t • Goal: user learns P(z) without revealing z. • Step 2: Secret Sharing of z General t: • zj = z+j 1+j 2 2+…+jt t • Step 3: Sj responds with P(zj) z Fm – User can extrapolate P(z) from P(z 1), …, P(zk) if k>dt. • Define deg-dt univariate poly Q(W)=P(z+W 1+W 2 2+…+Wt t) • P(z)=Q(0) can be extrapolated from dt+1 distinct values q(j) Ø O(n 1/d) communication using k=dt+1 servers.

Improved Variant [WY 05] • Goal: user learns P(z) without revealing z. • Step 2: Secret Sharing of z General t: • zj = z+j 1+j 2 2+…+jt t • Step 3: Sj responds with P(zj) along with all m partial derivatives of P evaluated at zj – User can extrapolate P(z) if k>dt/2. • Define deg-dt univariate poly Q(W)=P(z+W 1+W 2 2+…+Wt t) • P(z)=Q(0) can be extrapolated from 2 k>dt distinct values Q(j), Q’(j) • Complexity: O(m) communication both ways Ø Same communication using half as many servers!

Breaking the O(n 1/(2 k-1)) Barrier [BIKR 02] k=2 k=3 k=4 k=5 k=6

Arithmetization • As before, except that now F=GF(2) – Fix a degree parameter d (will be determined by k) • Goal: Communication = O(n 1/d) – User maps i [n] into a weight-d vector z of length m=O(n 1/d). • 1 11100…. 0 2 11010… 0 n 00… 0111 – Servers view x as a degree-d m-variate polynomial P(Z 1, …, Zm)= x 1 Z 1 Z 2 Z 3 + x 2 Z 1 Z 2 Z 4 + … + xn. Zm-2 Zm-1 Zm – Privately retrieving i-th bit of x privately evaluating P on z.

Effect of Degree Reduction degree d, m variables degree d/c, m variables size n size O(n 1/c)

Degree Reduction Using Partial Information ]BKL 95, BI 01] P S 1 P S 2 P Sk P(z) User z z is hidden from servers Q S 1 Q S 2 Q Sk Q(y) User y Each entry of y is known to all but one server.

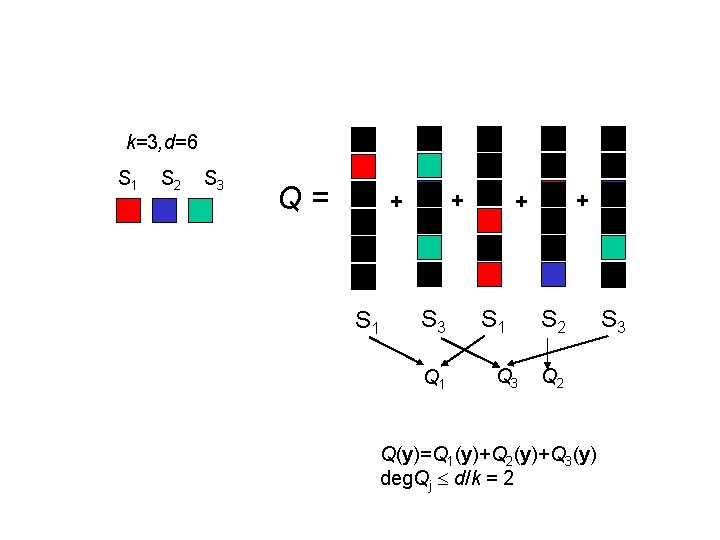
k=3, d=6 S 1 S 2 S 3 Q= + + S 1 S 3 Q 1 + + S 1 Q 3 S 2 Q(y)=Q 1(y)+Q 2(y)+Q 3(y) deg. Qj d/k = 2 S 3

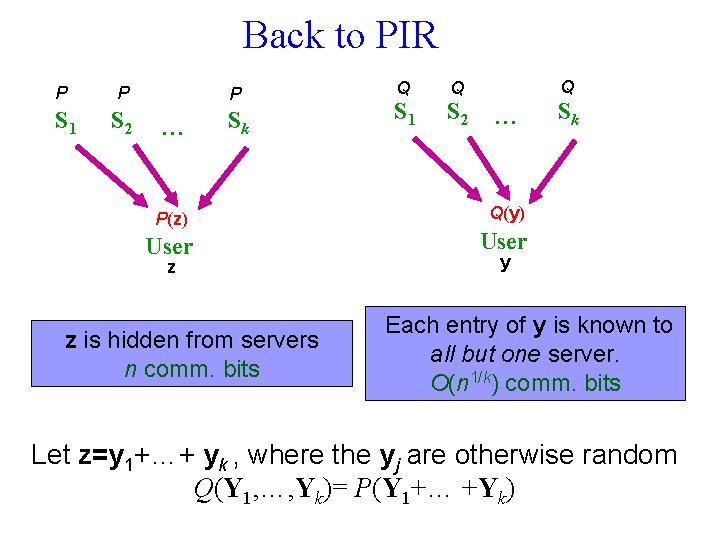
Back to PIR P P P S 1 S 2 Sk P(z) User z z is hidden from servers n comm. bits Q S 1 Q Q S 2 Sk Q(y) User y Each entry of y is known to all but one server. O(n 1/k) comm. bits Let z=y 1+…+ yk , where the yj are otherwise random Q(Y 1, …, Yk)= P(Y 1+… +Yk)

Initial Protocol O(m) = O(n 1/d) O(n 1/k) • User picks random y 1, …, yk s. t. y 1+…+ yk= z, and sends to Sj all y’s except yj. • Servers define an mk-variate degree-d polynomial Q(Y 1, …, Yk)= P(Y 1+… +Yk). • Each Sj computes degree-(d/k) poly. Qj , such that Q(y)= Q 1(y)+…+Qk(y). • Sj sends a description of Qj to User. • User computes Qj(y)=xi.

A Closer Look • M Sj missing at most d/k variables. deg Qj d/k Best previous binary PIR Best previous PIR Useful parameters: • d=k-1 query length O(n 1/(k-1)) d/k =0 answer length 1 • d=2 k-1 query length O(n 1/(2 k-1)) d/k =1 answer length O(n 1/(2 k-1))

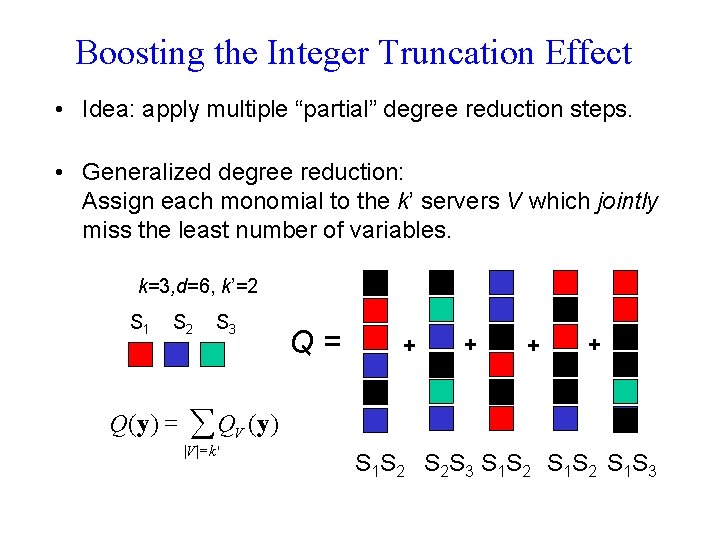
Boosting the Integer Truncation Effect • Idea: apply multiple “partial” degree reduction steps. • Generalized degree reduction: Assign each monomial to the k’ servers V which jointly miss the least number of variables. k=3, d=6, k’=2 S 1 S 2 Q(y ) = S 3 Q= + + å QV (y ) |V | = k ' S 1 S 2 S 2 S 3 S 1 S 2 S 1 S 3

replication reduction k k’ reduction k” reduction … 1 degree d size n d’ n’=O(n d’/d) n”=O(n’ d ”/d’) … d” … n d/k /d d/k The missing operator: k conversion k d d’ n n #vars m m’=O(md/d’) Additional cost: re-distribute new point y’

Example: k=3 replication reduction 3 2 conversion 2 reduction 1 degree #vars 7 O(n 1/7) 4 O(n 1/7) 3 O(n 4/21) 1 O(n 4/21) Queries O(n 4/21) size n O(n 4/7) O(n 4/21) Answers communication

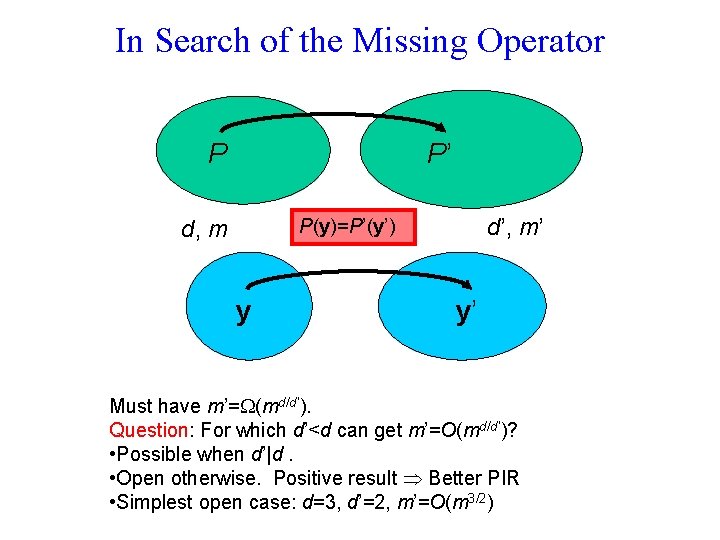
In Search of the Missing Operator P P’ d’, m’ P(y)=P’(y’) d, m y y’ Must have m’= (md/d’). Question: For which d’<d can get m’=O(md/d’)? • Possible when d’|d. • Open otherwise. Positive result Better PIR • Simplest open case: d=3, d’=2, m’=O(m 3/2)

A Workaround • Can’t solve the polynomial conversion problem in general. • … but easy to solve given the promise weight(y)=const. • Stronger degree reduction: • Main technical lemma: good parameters for strong degree reduction.

Open Problems • Better upper bounds – Known: O(ncloglogk /(klogk)) – What is the true limit of our technique? • Generalize best upper bound to t>1 • Tight bounds for polynomial conversion • Lower bounds – Known: clogn – Simplest cases: • k=2 • k=3, single answer bit per server