Randomization Techniques for Multiparty Computation Yuval Ishai Technion

Randomization Techniques for Multiparty Computation Yuval Ishai Technion 0

Lesson • “Unconditionally secure cryptography” is useful! – … even if you don’t care about unconditional security – … even if you don’t care about cryptography • Today: randomization techniques parallel crypto • Tomorrow: PIR locally decodable codes 1

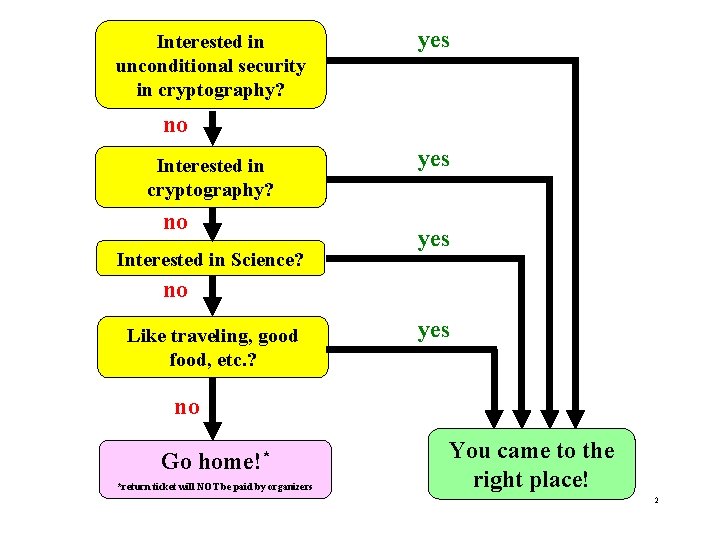
Interested in unconditional security in cryptography? yes no Interested in cryptography? no Interested in Science? yes no Like traveling, good food, etc. ? yes no Go home!* *return ticket will NOT be paid by organizers You came to the right place! 2

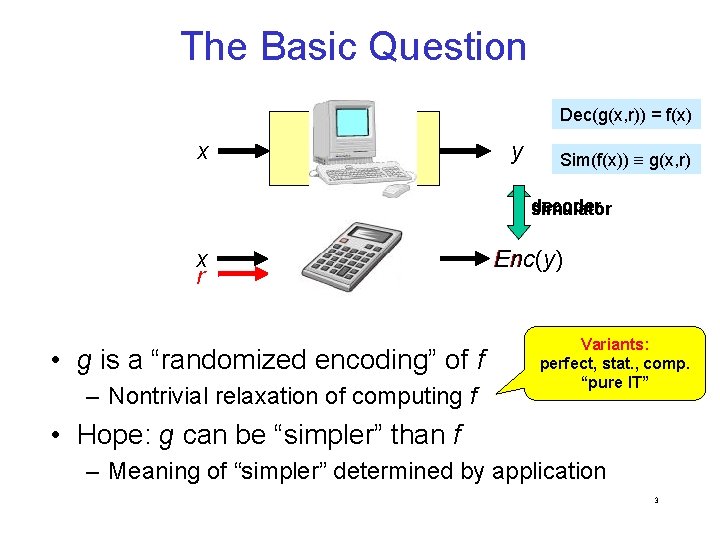
The Basic Question Dec(g(x, r)) = f(x) x f y Sim(f(x)) g(x, r) decoder simulator x r g • g is a “randomized encoding” of f – Nontrivial relaxation of computing f Enc(y) Variants: perfect, stat. , comp. “pure IT” • Hope: g can be “simpler” than f – Meaning of “simpler” determined by application 3

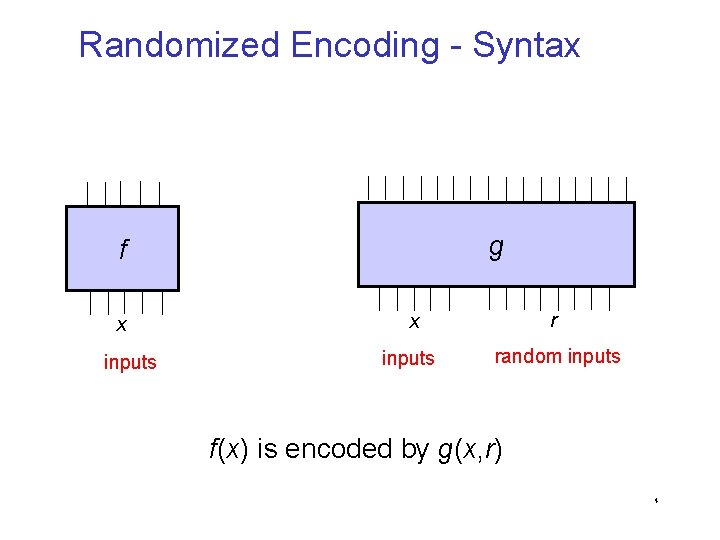
Randomized Encoding - Syntax g f x inputs x r inputs random inputs f(x) is encoded by g(x, r) 4

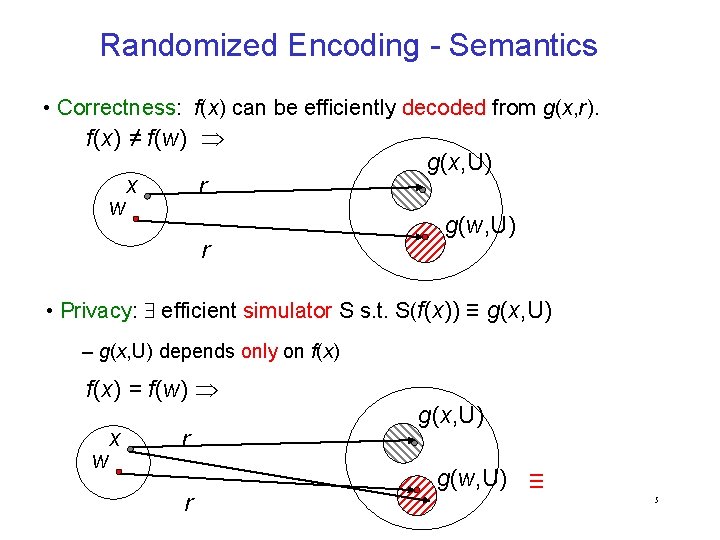
Randomized Encoding - Semantics • Correctness: f(x) can be efficiently decoded from g(x, r). f(x) ≠ f(w) w x r r g(x, U) g(w, U) • Privacy: efficient simulator S s. t. S(f(x)) ≡ g(x, U) – g(x, U) depends only on f(x) = f(w) w x r r g(x, U) g(w, U) ≡ 5

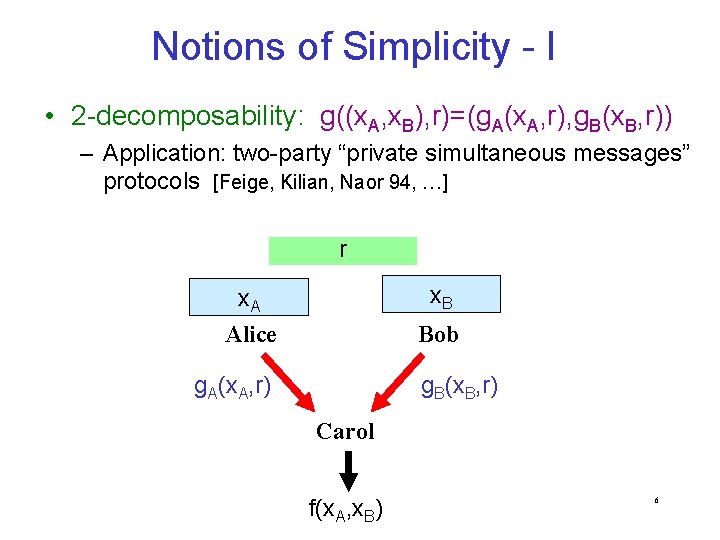
Notions of Simplicity - I • 2 -decomposability: g((x. A, x. B), r)=(g. A(x. A, r), g. B(x. B, r)) – Application: two-party “private simultaneous messages” protocols [Feige, Kilian, Naor 94, …] r x. A x. B Alice Bob g. A(x. A, r) g. B(x. B, r) Carol f(x. A, x. B) 6

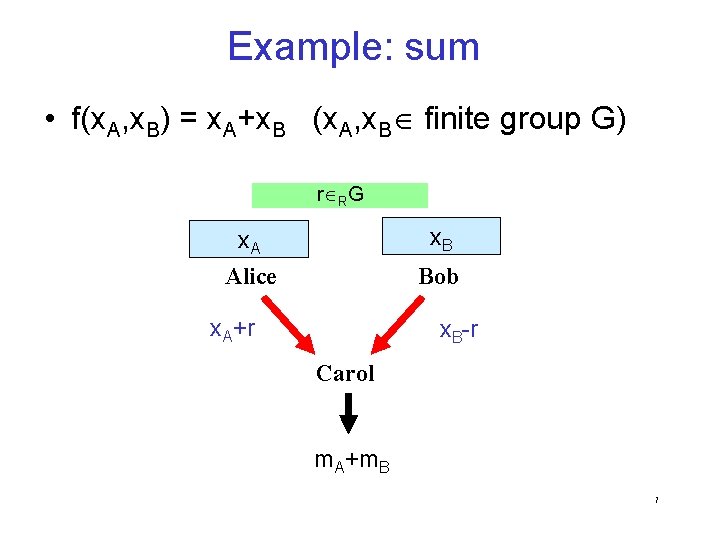
Example: sum • f(x. A, x. B) = x. A+x. B (x. A, x. B finite group G) r RG x. A x. B Alice Bob x. A+r x. B-r Carol m. A+m. B 7

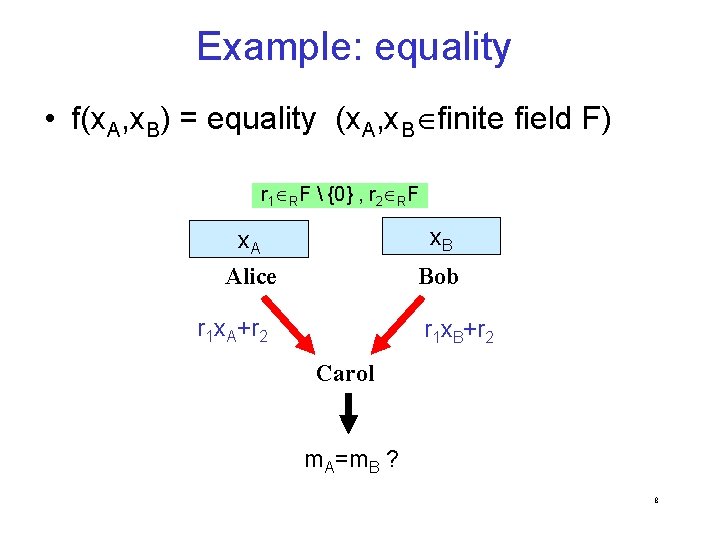
Example: equality • f(x. A, x. B) = equality (x. A, x. B finite field F) r 1 RF {0} , r 2 RF x. A x. B Alice Bob r 1 x. A+r 2 r 1 x. B+r 2 Carol m. A = m. B ? 8

Example: ANY function • f(x. A, x. B) = x. A x. B (x. A, x. B {0, 1}) – Reduction to equality: x. A 1/0, x. B 2/0 • General boolean f: write as disjoint 2 -DNF – f(x. A, x. B) = (a, b): f(a, b)=1 (x. A=a x. B=b) = t 1 t 2 … tm t 1 s ts+1 t 2. . . tts-1 m Exponential complexity 000000 0 00000100000 1 9

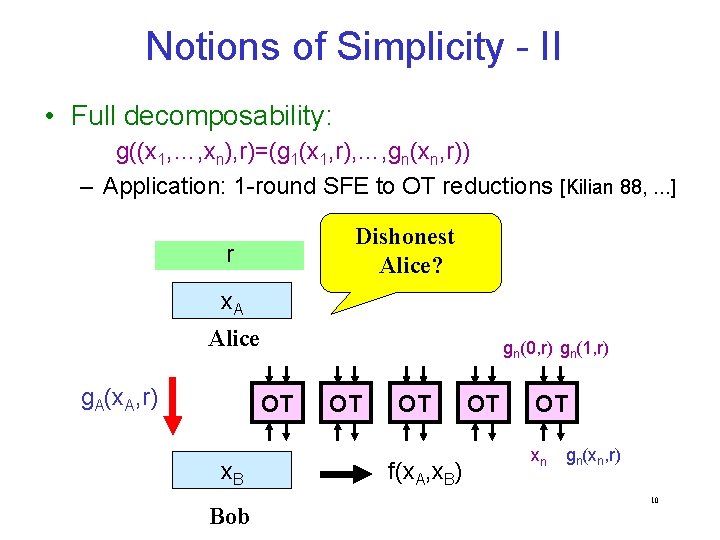
Notions of Simplicity - II • Full decomposability: g((x 1, …, xn), r)=(g 1(x 1, r), …, gn(xn, r)) – Application: 1 -round SFE to OT reductions [Kilian 88, . . . ] Dishonest Alice? r x. A Alice g. A(x. A, r) gn(0, r) gn(1, r) OT x. B Bob OT OT f(x. A, x. B) OT OT xn gn(xn, r) 10

Example: iterated group product • Abelian case – f(x 1, …, xn)=x 1+x 2+…+xn – g(x, (r 1, …, rn-1)) = x 1+r 1 x 2+r 2 … xn-1+rn-1 xn-r 1 -…-rn-1 • General case [Kil 88] – f(x 1, …, xn)=x 1 x 2 …xn – g(x, (r 1, …, rn-1)) = x 1 r 1 r 1 -1 x 2 r 2 r 2 -1 x 2 r 3 … rn-2 -1 xn-1 rn-1 -1 xn 11

Example: iterated group product Thm [Barrington 86] Every boolean f NC 1 can be computed by a poly-length, width-5 branching program. 1 r 1 r 1 -1 2 r 2 rm-1 -1 m f(x 1, …, xn) reduces to 1 2 … m where: • i S 5 f Each i depends on a single xj • • g distinct 0, 1 S 5 s. t. 1 2 … m = f(x) x 1 x 2 … xn r 1 r 2 . . … rm-1 Encoding iterated group product -1 r on -1 ra single -1 of x output bit of g depends just bit • 1 Every … r r r … r 2 3 m 1 1 1 2 2 2 3 3 m-1 m Ø Efficient fully decomposable encoding for every f NC 1 12

Notions of Simplicity - III • Low degree: g(x, r) = vector of degree-d poly in x, r over F – aka “Randomizing Polynomials” [I, Kushilevitz 00, …] – Application: round-efficient MPC • Motivating observation: Low-degree functions are easy to distribute! – Round complexity of MPC protocols [BGW 88, CCD 88, CDM 00, …] • Semi-honest model – t<n/d 2 rounds – t<n/2 multiplicative depth + 1 = log d +1 rounds • Malicious model – Optimal t O(log d) rounds – Randomized func. g reduces to a deterministic degree-d func. g’ • g’((x 1, r 1), … , (xn, rn)) = g((x 1, …, xn), (r 1+…+rn)) • Security of reduction is “model independent” 13

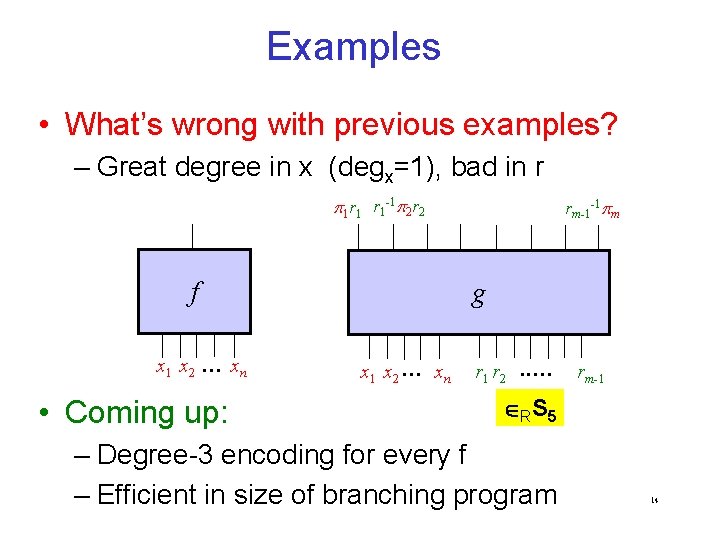
Examples • What’s wrong with previous examples? – Great degree in x (degx=1), bad in r 1 r 1 r 1 -1 2 r 2 f x 1 x 2 … xn • Coming up: rm-1 -1 m g x 1 x 2 … xn r 1 r 2 . . … rm-1 RS 5 – Degree-3 encoding for every f – Efficient in size of branching program 14

Notions of Simplicity - IV • Small locality: x r – Application: parallel cryptography! [Applebaum, I, Kushilevitz 04, …] • Coming up: encodings with locality 4 – degree 3, fully decomposable – efficient in size of branching program 15

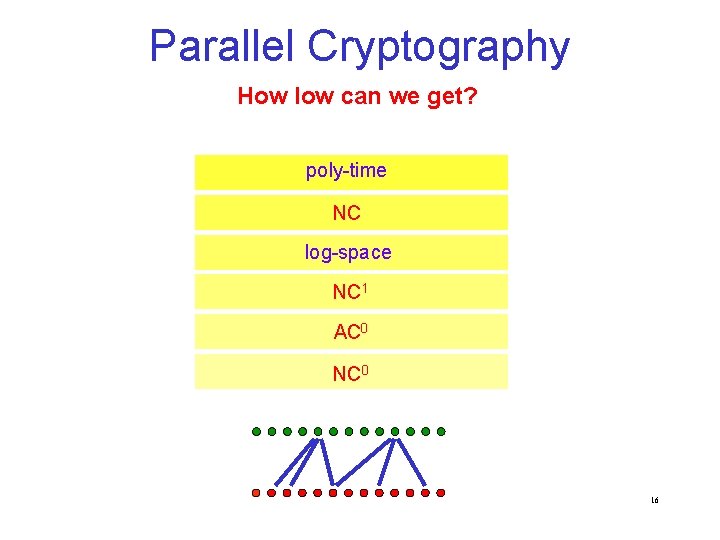
Parallel Cryptography How low can we get? poly-time NC log-space NC 1 AC 0 NC 0 16

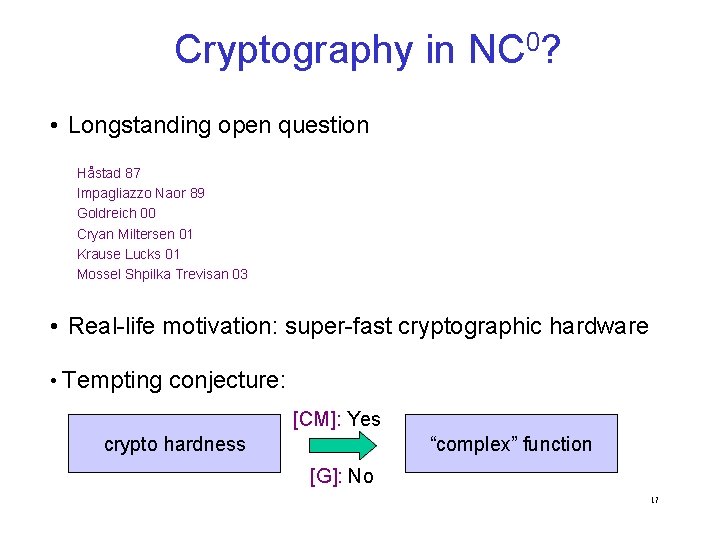
Cryptography in NC 0? • Longstanding open question Håstad 87 Impagliazzo Naor 89 Goldreich 00 Cryan Miltersen 01 Krause Lucks 01 Mossel Shpilka Trevisan 03 • Real-life motivation: super-fast cryptographic hardware • Tempting conjecture: [CM]: Yes crypto hardness “complex” function [G]: No 17

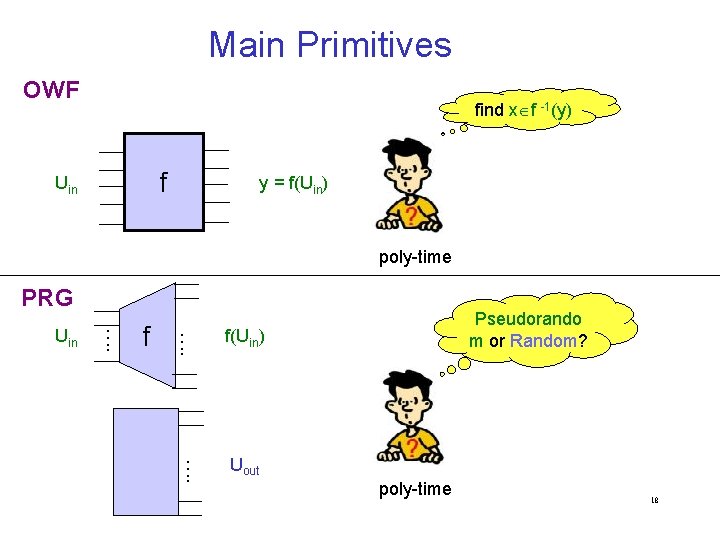
Main Primitives OWF find x f -1(y) f Uin y = f(Uin) poly-time PRG f …. Uin Pseudorando m or Random? f(Uin) …. Uout poly-time 18

Surprising Positive Result [AIK 04] Compile primitives in a “relatively high” complexity class (e. g. , NC 1, NL/poly, L/poly) into ones in NC 0. NC 1 cryptography implied by factoring, discrete-log, lattices… locality 4 essentially settles open question OWF factoring, discrete-log, lattices, … subset-sum impossible low stretch NC 1 TC 0 AC 0 NC 04 open NC 04 NC 03 NC 02 PRG OWF open 19

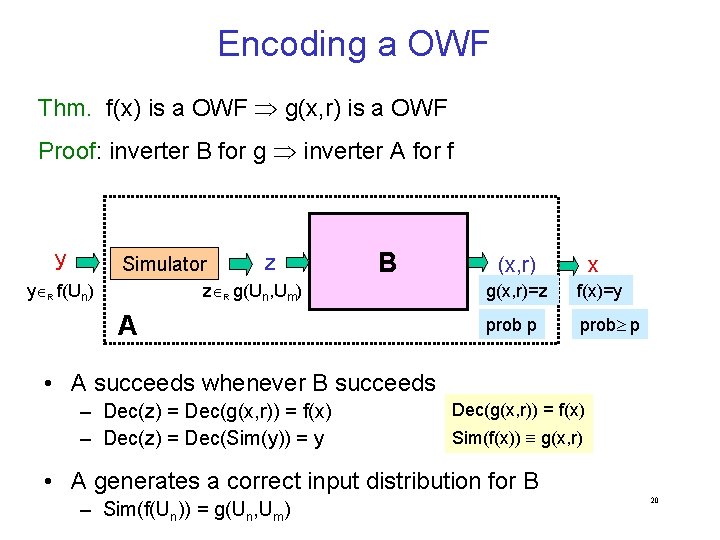
Encoding a OWF Thm. f(x) is a OWF g(x, r) is a OWF Proof: inverter B for g inverter A for f y Simulator y R f(Un) z B z R g(Un, Um) A x (x, r) g(x, r)=z f(x)=y prob p • A succeeds whenever B succeeds – Dec(z) = Dec(g(x, r)) = f(x) – Dec(z) = Dec(Sim(y)) = y Dec(g(x, r)) = f(x) Sim(f(x)) g(x, r) • A generates a correct input distribution for B – Sim(f(Un)) = g(Un, Um) 20

Encoding a PRG • Want: f(x) is a PRG g(x, r) is a PRG • Problems: – output of g may not be pseudorandom – g may shrink its input • Solution: “perfect” randomized encoding – respects pseudorandomness, additive stretch, … – stretch of g is typically sublinear even if that of f is superlinear – most (not all) known constructions give perfectness for free 21

Additional Cryptographic Primitives • General compiler also applies to: – – – one-way / trapdoor permutations collision-resistant hashing public key / symmetric encryption signatures / MACs commitments … • Caveat: decryption / verification not in NC 0… – … But: can commit in NC 0 with decommit in NC 0[AND] – Applications: coin-flipping, zero-knowledge, … 22

Non-cryptographic PRGs • ε-biased generators [Mossel Shpilka Trevisan 03]: superlinear stretch in NC 05 – Current work: linear stretch in NC 03 • optimal locality, stretch • PRGs for space-bounded computation 23

Remaining Challenge Coming up… 0 How to encode “complex” f by g NC ? • Observation: enough to obtain const. degree encoding • Locality Reduction: degree 3 poly over GF(2) locality 4 rand. encoding f(x) = g(x, r, s) = T 1(x) + T 2(x) + … + Tk(x) T 1(x)+r 1 T 2(x)+r 2 … Tk(x)+rk –r 1+s 1 –r 2 +s 2 … –sk-1–rk 24

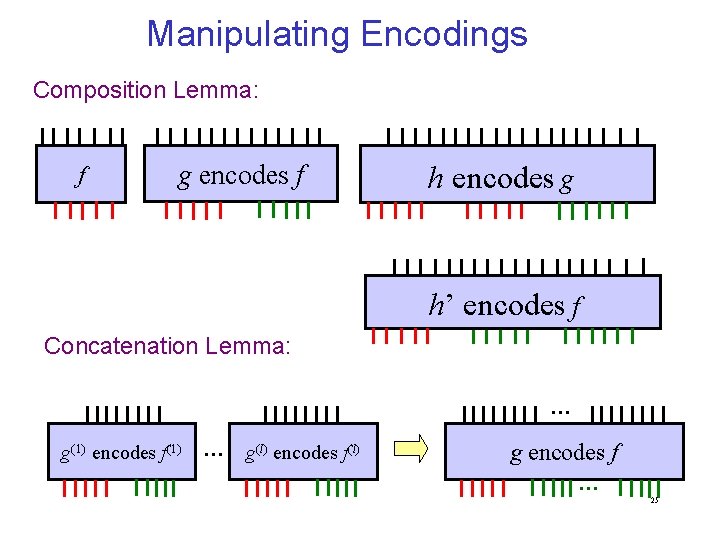
Manipulating Encodings Composition Lemma: f g encodes f h encodes g h’ encodes f Concatenation Lemma: … g(1) encodes f(1) … g(l) encodes f(l) g encodes f … 25

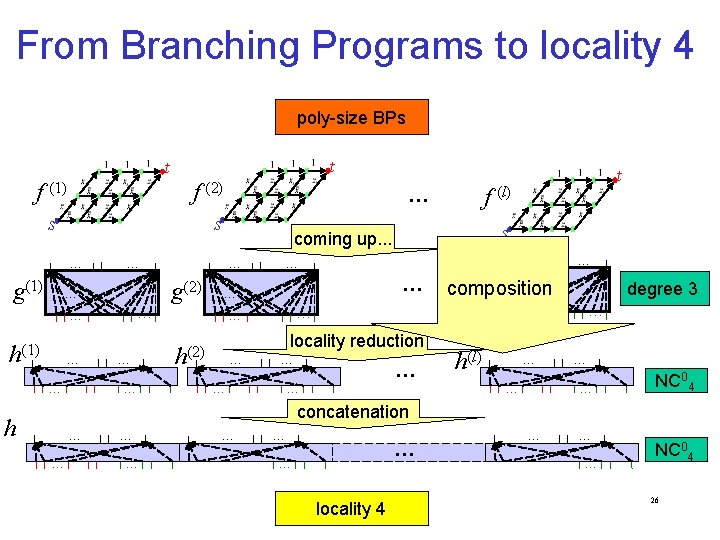
From Branching Programs to locality 4 poly-size BPs t t s … g(1) … … h(1) … … … g(2) s … … … locality reduction h(2) … … … t f (l) coming up. . . … s … f (2) … … … composition g(l) … degree 3 … … h(l) … … NC 04 concatenation h … … … … f (1) … locality 4 … … NC 04 26

3 Ways to Degree 3 1. Degree-3 encoding using a circuit representation y 3 y 1 x 2 y 2 x 3 x 4 x 5 f(x)=1 y 1 , y 2 , y 3 y 1=NAND(x 1 , x 2)= x 1(1 -x 2)+(1 -x 1)x 2+(1 -x 1)(1 -x 2) y 2=NAND(x 3 , x 4) y 3=NAND(y 1 , y 2) 1 =NAND(y 3 , x 5) Note: ! y 1, y 2 , y 3 27

Using circuit representation (contd. ) q 1(x, y)=0 q 2(x, y)=0. . . qk(x, y)=0 deg. -2 p(x, y, r)= ri qi(x, y) deg. -3 f(x)=0 P(x) is uniform f(x)=1 P(x) 0 given y=y 0, otherwise it is uniform Statistical distance amplified to 1/2 by 2 (k) repetitions. • works over any field • complexity exponential in circuit size 28

2. Degree-3 encoding using quadratic characters Fact from number theory: • Let N=2 n, b = length-N truth-table of f, F=GF(q) • Define p(x 1, …, xn, r) = • one polynomial • huge field size 29

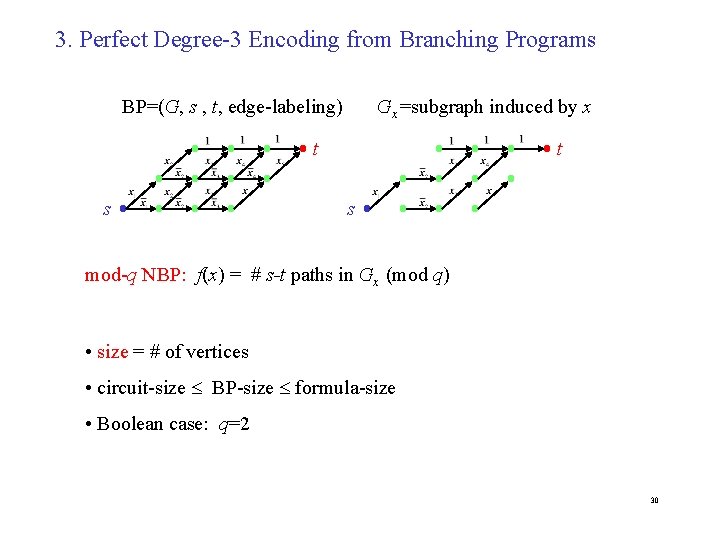
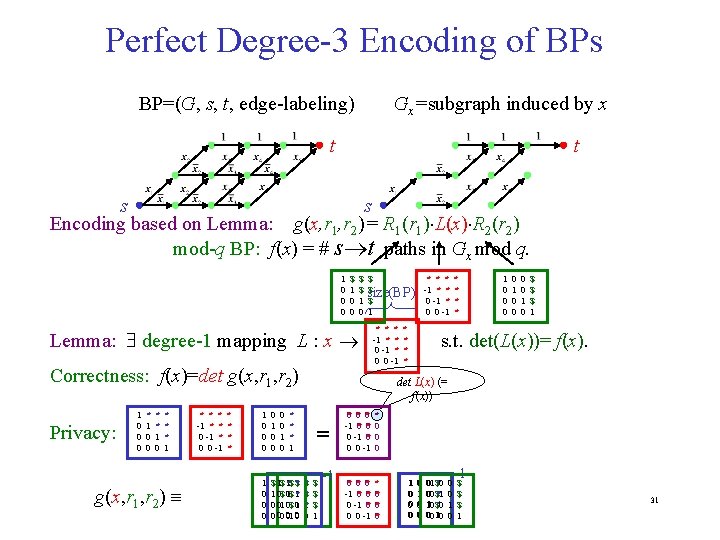
3. Perfect Degree-3 Encoding from Branching Programs BP=(G, s , t, edge-labeling) Gx=subgraph induced by x t t s s mod-q NBP: f(x) = # s-t paths in Gx (mod q) • size = # of vertices • circuit-size BP-size formula-size • Boolean case: q=2 30

Perfect Degree-3 Encoding of BPs BP=(G, s, t, edge-labeling) Gx=subgraph induced by x t t s s Encoding based on Lemma: g(x, r 1, r 2)= R 1(r 1) L(x) R 2(r 2) mod-q BP: f(x) = # s t paths in Gx mod q. 1 0 0 0 $ 1 0 0 $ $ 1 0 $ * * * $ -1 size(BP ) 0 -1* ** $ 1 0 0 -1 Lemma: degree-1 mapping L : x Correctness: f(x)=det g(x, r 1, r 2) Privacy: 1 0 0 0 * 1 0 0 * * 1 0 * * * 1 g(x, r 1, r 2) * * * -1 * * 0 -1 * 0 0 -1 * * 1 0 0 0 0 1 0 0 0 $ 1$ *$ 1 0$ 10$ *1 0 01 0$ 10 0 00 01 0 * * * -1 * * 0 -1 * 0 0 -1 * * * * 1 0 0 0 0 1 0 $ $ $ 1 s. t. det(L(x))= f(x). det L(x) (= f(x)) * * * 1 = *$ *$ *1 10 $ $ $ 1 -1 0* 0* 0* -1 0* 0* 0 -1 0* 0 0 -1 * 0 0* *0 *0 -1 *0 *0 0 -1 *0 0 0 -1 * *0 *0 *0 11 00 00 001 $*0 000 $*1 110 $*0 000 110 0 0 1 0 -1 $ $ $ 1 31

Proof of Lemma: degree-1 mapping L : x * * * -1 * * 0 -1 * 0 0 -1 * * s. t. det(L(x))= f(x). Proof: A(x)= adjacancy matrix of Gx (over F=GF(q)) A* = I+A+A 2+… = (I-A)-1 A*s, t = (-1)s+t det (I-A)|t, s / det (I-A) = det (A-I)|t, s L(x)= (A(x)-I)|t, s s s L= A t 0 * -1 0 0 0 0 t * * * 0 -1 * * 0 0 -1 * 0 0 -1 0 32

Thm. size-s BP degree 3 encoding of size O(s 2) • perfect encoding for mod-q BP (capturing L/poly for q=2) ü large q: useful for (comp. -secure) two-party computation • imperfect for nondeterministic BP (capturing NL/poly) 33

The secure evaluation of an arbitrary functionality can be reduced to the secure evaluation of degree-3 polynomials. Q: How many rounds? • How many rounds for maximal privacy? 3 rounds suffice • How much privacy in 2 rounds? t<k/3 suffices • perfect privacy + correctness • complexity O(BP-size 2) 34

Is 3 minimal? Thm. [IK 00] A boolean function f admits a perfectly private degree-2 encoding over F if and only if either: • f or its negation test for a linear condition Ax=b over F; • f admits standard representation by a degree-2 polynomial over F. 35

Computationally Private Encodings [AIK 05] • Known: f L encoding in NC 0 • Goal: f P encoding in NC 0 • Idea: relax encoding requirement x r comp g Enc(y) • Respects security of most primitives • Thm: f P computational encoding in NC 04 assuming “easy PRG” (min-PRG L) ü “Easy PRG” can be based on factoring, discrete-log, lattices 36

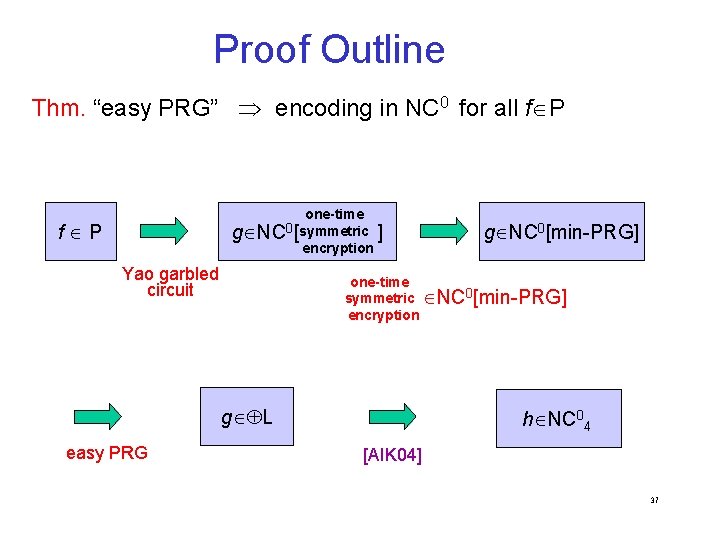
Proof Outline Thm. “easy PRG” encoding in NC 0 for all f P one-time g NC 0[symmetric ] encryption f P Yao garbled circuit one-time symmetric NC 0[min-PRG] encryption g L easy PRG g NC 0[min-PRG] h NC 04 [AIK 04] 37

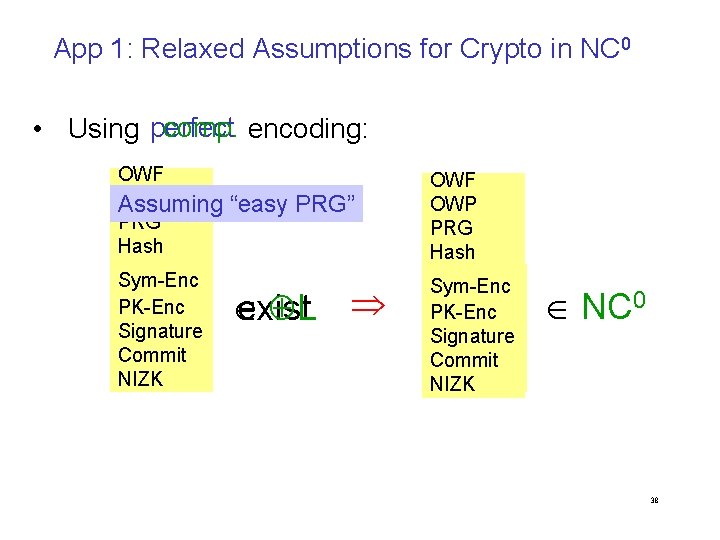
App 1: Relaxed Assumptions for Crypto in NC 0 comp. encoding: • Using perfect OWF OWP Assuming PRG Hash Sym-Enc PK-Enc Signature Commit NIZK “easy PRG” exist L OWF OWP PRG Hash Sym-Enc PK-Enc Signature Commit NIZK NC 0 38

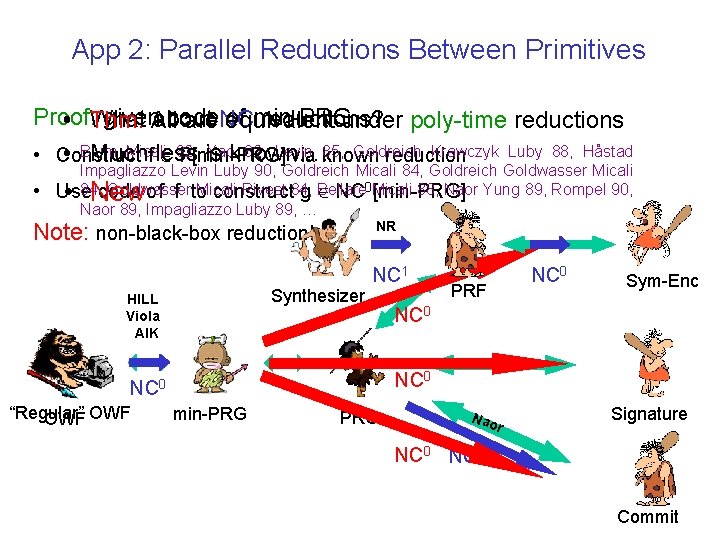
App 2: Parallel Reductions Between Primitives Proof: given. All code of min-PRG What about reductions? • Thm. are. NC equivalent under poly-time reductions Micali Yaoknown…. 82, Levin 85, Goldreich Krawczyk Luby 88, Håstad • Blum Much is • Construct f less 82, P[min-PRG] via known reduction • Impagliazzo Levin Luby 90, Goldreich Micali 84, Goldreich Goldwasser Micali 84, code Goldwasser Micali Rivest 84, Bellare 88, Naor Yung 89, Rompel 90, Use of f to construct g NC 0 Micali [min-PRG] Naor 89, Impagliazzo Luby 89, … • New NR Note: non-black-box reduction! NC 1 Synthesizer HILL Viola AIK PRF Sym-Enc NC 0 “Regular” OWF NC 0 min-PRG Nao r Signature NC 0 39 Commit

App 3: Secure Multiparty Computation In case you don’t insist on unconditional security… • Secure computatoin of every func. f efficiently reduces to deg-3 poly … asuming “easy PRG” • In particular: Protocols desribed by Ivan imply const. round computationally secure MPC for every f (Known assuming any PRG [BMR 90, DI 05]; however, current approach is conceptually simpler. ) 40

Summary • Different flavors of randomized encoding – Motivated by different applications • Round-efficient secure computation • Parallel cryptography • “Simplest” encodings: outputs of form xirjrk+rh – Efficient for various “intermediate complexity” classes (NC 1, NL/poly, modq. L/poly) • Algebraic approach • “Combinatorial” approach: information-theoretic garbled circuit – Computationally private encodings: efficient for all P (assuming “Easy PRG”) 41

Open Questions Randomized encoding Unconditionally secure MPC poly-size NC 0 encoding for every f P? efficient constantround protocol for every f P? locality 3 for every f? better encodings? maximal privacy with minimal interaction? better const-round protocols? Parallel crypto OWF in NC 0? OWF in NC 1 OWF in NC 03? practical hardware? 42