Forms of Retrieval Sequential Retrieval TwoStep Retrieval Retrieval

Forms of Retrieval • Sequential Retrieval • Two-Step Retrieval • Retrieval with Indexed Cases

Retrieval with Indexed Cases Sources: –Textbook, Chapter 7 –Davenport & Prusack’s book on Advanced Data Structures –Samet’s book on Data Structures

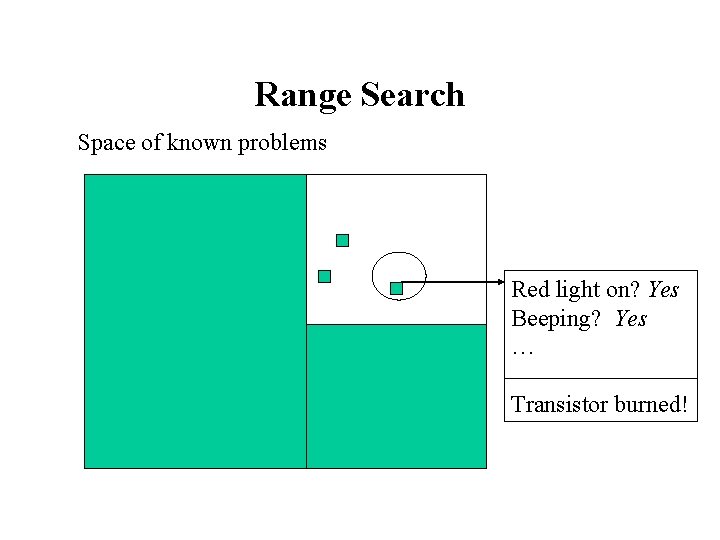
Range Search Space of known problems Red light on? Yes Beeping? Yes … Transistor burned!

k-d Trees • Idea: Partition of the case base in smaller fragments • Representation of a k-dimensional space in a binary tree • Similar to a decision tree: comparison with nodes • During retrieval: ØSearch for a leaf, but ØUnlike decision trees backtracking may occur

Definition: k-d Trees • Given: ØK types: T 1, …, Tk for the attributes A 1, …, Ak ØA case base CB containing cases in T 1 … Tk ØA parameter b (size of bucket) • A K-D tree T(CB) for a case base CB is a binary tree defined as follows: ØIf |CB| < b then T(CB) is a leaf node (a bucket) ØElse T(CB) defines a tree such that: §The root is marked with an attribute Ai and a value v in Ai and §The 2 k-d trees T({c CB: c. i-attribute < v}) and T({c CB: c. i-attribute v}) are the left and right subtrees of the root

BWB-Check • Ball-With in-Bounds check: Ø Suppose that algorithm reaches a leave node M (with at most b cases) while searching for the most similar case to P Ø Let c be a case in B such that dist(c, P) is the smallest Ø Then c is a candidate NN for P Ø For each boundary B of M, dist(P, B) > dist(c, P) then c is the NN Ø But if for any boundary B of M, if dist(P, B) < dist(c, P) then the algorithm needs to backtrack and check if in the regions of B, there is a better candidate Ø For computing distance, simply use: f-1 be the inverse of the distance-similarity compatible function: Ø distance(P, C) = f-1(sim(P, C))

BOB-Check • Ball-Out of-Bounds check: Ø Used during backtracking Ø Checks if for the boundary B defined in the node: dist(P, B) < dist(c, P) q. Where c is our current candidate for best case (e. g. , the closest case to P in the initial bucket) Ø If the condition is true, The algorithm needs to check if in those boundary’s regions, there is a better candidate

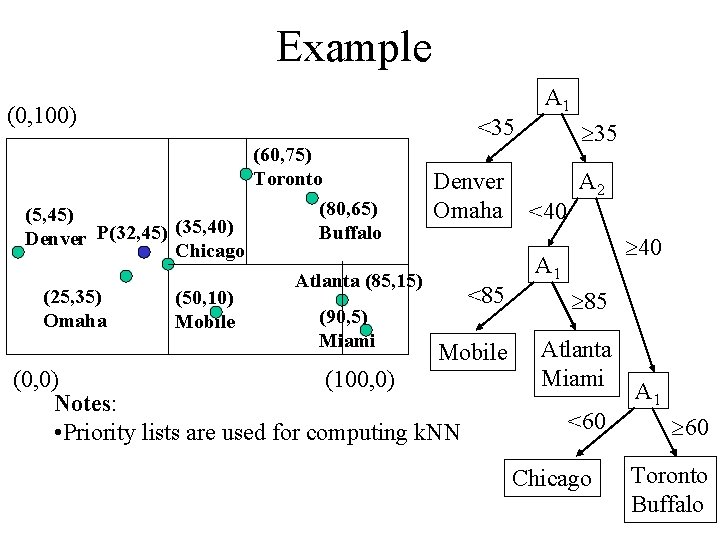
Example (0, 100) (60, 75) Toronto (80, 65) (5, 45) (35, 40) Buffalo Denver P(32, 45) Chicago Atlanta (85, 15) (25, 35) (50, 10) (90, 5) Omaha Mobile Miami <35 Denver Omaha <85 Mobile (0, 0) (100, 0) Notes: • Priority lists are used for computing k. NN A 1 35 <40 A 2 40 A 1 85 Atlanta Miami <60 Chicago A 1 60 Toronto Buffalo

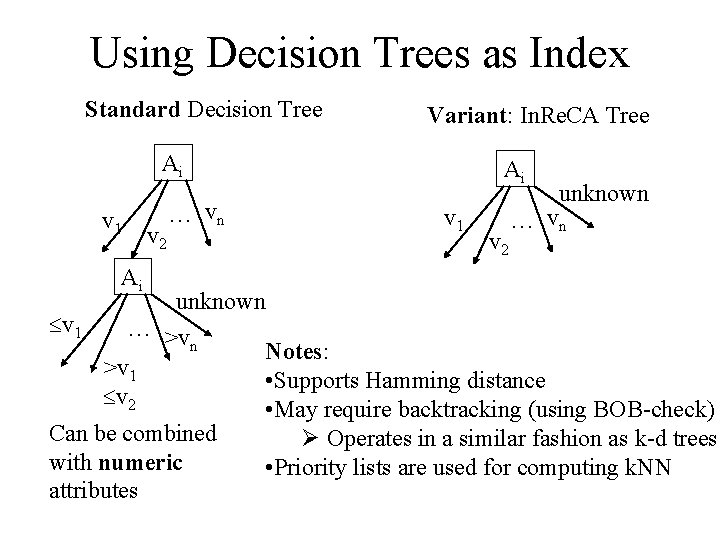
Using Decision Trees as Index Standard Decision Tree Variant: In. Re. CA Tree Ai v 1 Ai v 2 … vn Ai v 1 v 2 unknown … vn unknown v 1 … >v n Notes: >v 1 • Supports Hamming distance v 2 • May require backtracking (using BOB-check) Can be combined Ø Operates in a similar fashion as k-d trees with numeric • Priority lists are used for computing k. NN attributes

Properties of Retrieval with Indexed Cases • Advantage: ØEfficient retrieval ØIncremental: don’t need to rebuild index again every time a new case is entered Ø -error does not occur • Disadvantages: ØCost of construction is high ØOnly work for monotonic similarity relations