Priority Queue Heap CSCI 3110 Nan Chen Priority

Priority Queue & Heap CSCI 3110 Nan Chen

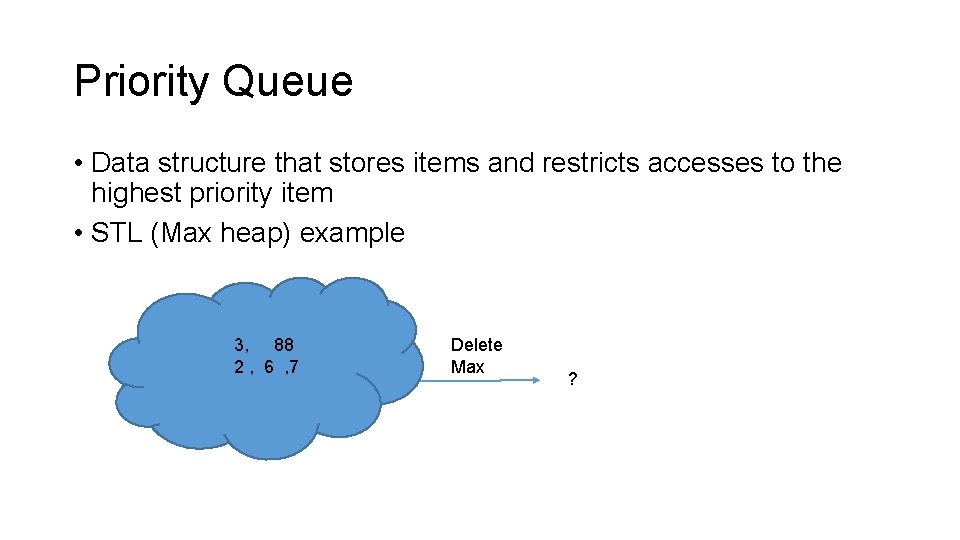
Priority Queue • Data structure that stores items and restricts accesses to the highest priority item • STL (Max heap) example 3, 88 2 , 6 , 7 Delete Max ?

Applications of priority queue • Solve 0/1 Knapsack Problem (Branch and Bound ) …

Implementation of Priority Queue • Linked list: Insert O(1) , top/pop(N) • Sorted Linked list: Insert O(N) , top/pop(1) • Search Tree: Overkill (supports many operations that we don't need) and issues

Problem of Binary Search Tree Imp. • Pop( ) What if we have many items to pop from the heap Repeatedly removing a node that is in the right subtree would seem to hurt the balance of the tree by making the left subtree heavy. • The natural implementation for a priority queue is a (binary) heap

(Binary) Heaps • Structure property: Complete binary tree • (Max) Heap order property: Value of a node >= value of children (Min) Heap order property: Value of a node <= value of children

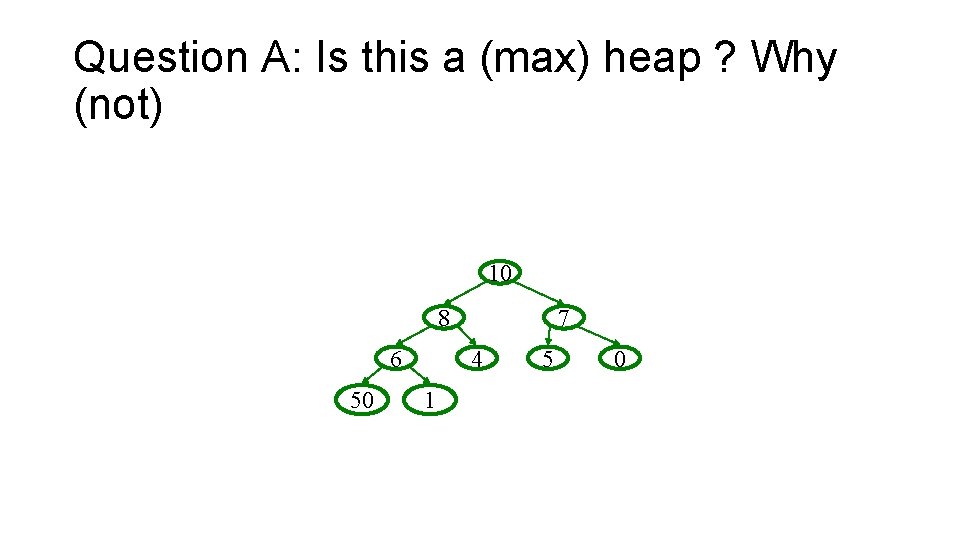
Question A: Is this a (max) heap ? Why (not) 10 8 6 50 7 4 1 5 0

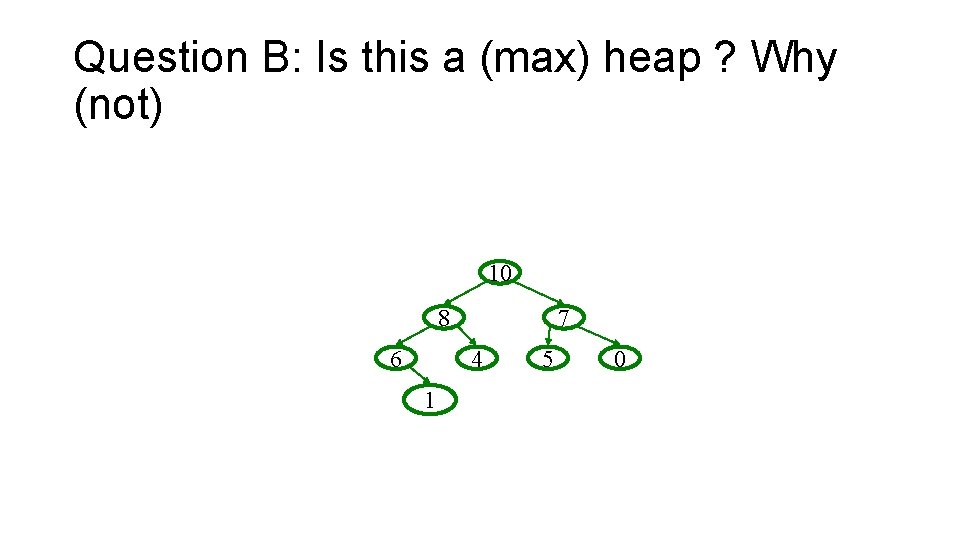
Question B: Is this a (max) heap ? Why (not) 10 8 6 7 4 1 5 0

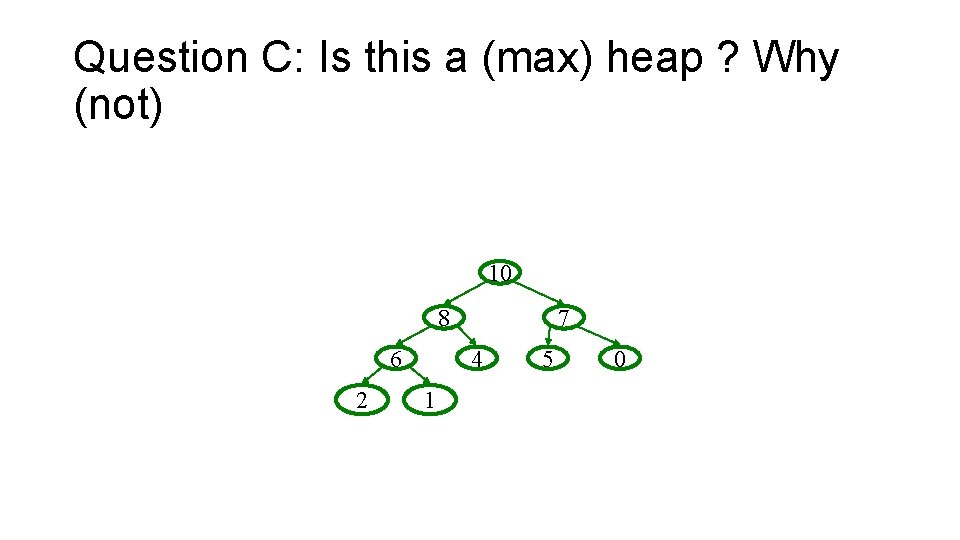
Question C: Is this a (max) heap ? Why (not) 10 8 6 2 7 4 1 5 0

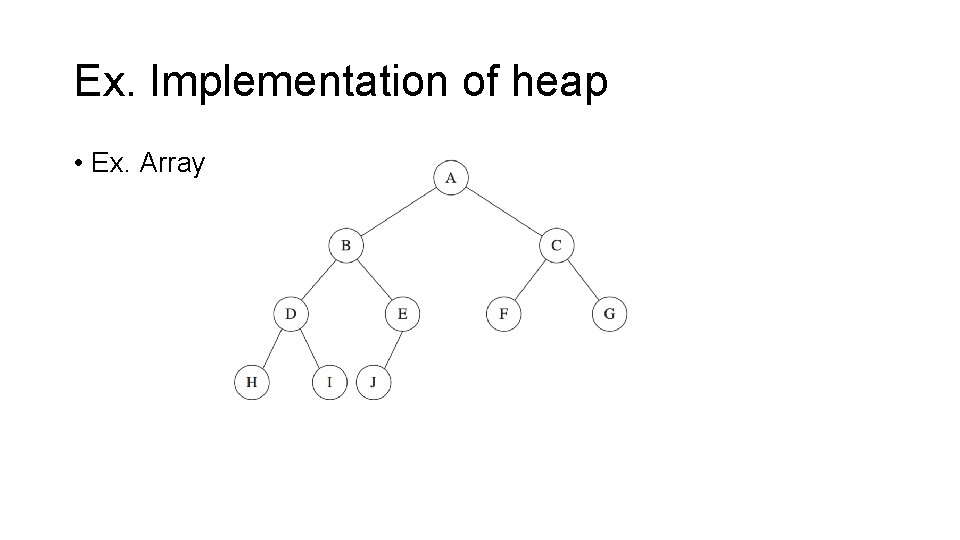
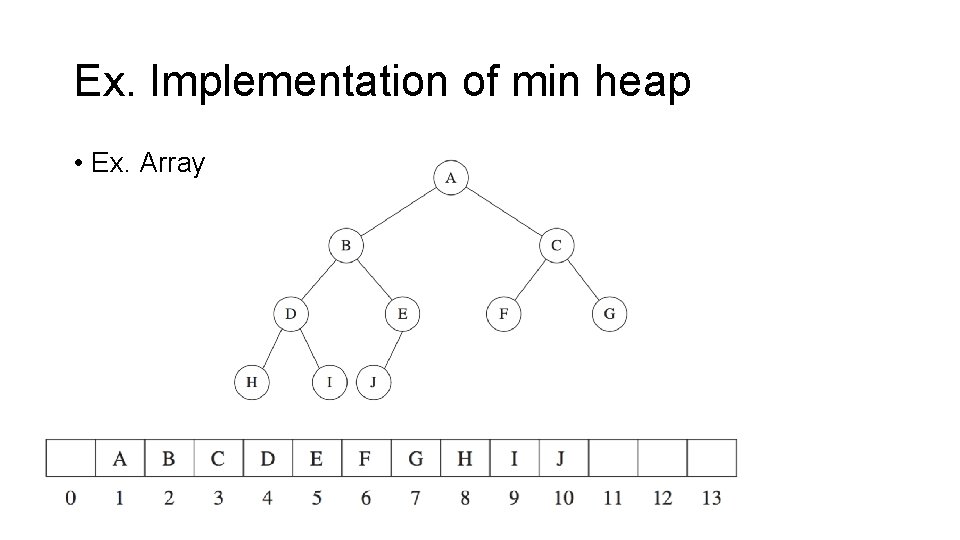
Ex. Implementation of heap • Ex. Array

Ex. Implementation of min heap • Ex. Array

Index mapping between parent and childen • If the parent is the i th position in an array Left child : 2 i Right child : 2 i+1 • If child is at i th position in an array Parent : Floor ( i / 2)

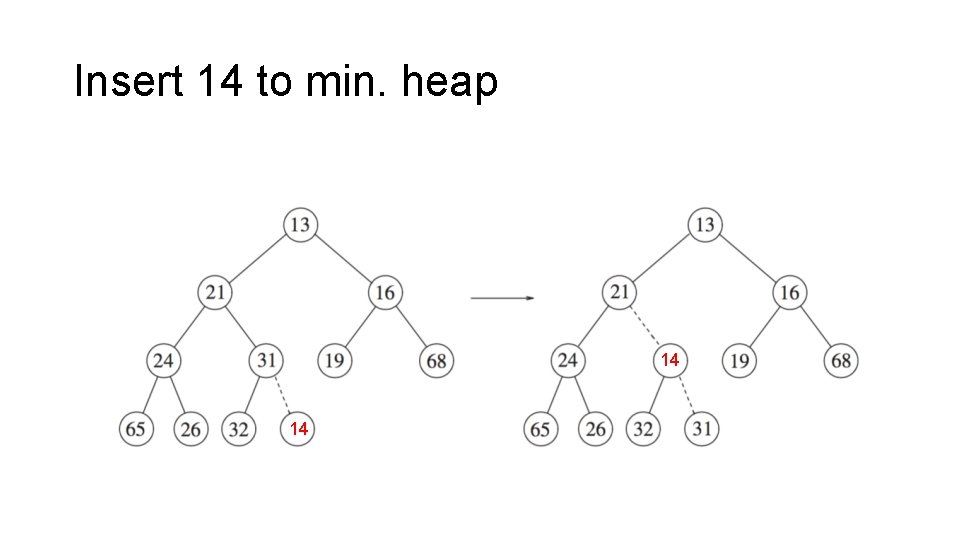
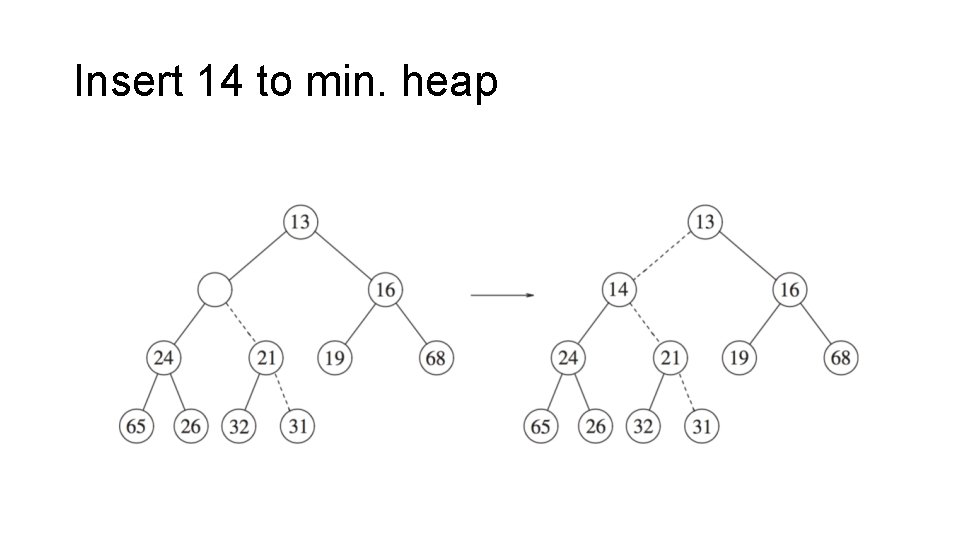
Insert (inserts an item) to heap 1) Add to last index in array (resize if necessary) -> If X can be placed in the hole without violating heap order, done -> other wise (add X violates heap order , go to step 2 ) 2) Bubble up ( percolate up )

Insert 14 to min. heap 14 14

Insert 14 to min. heap

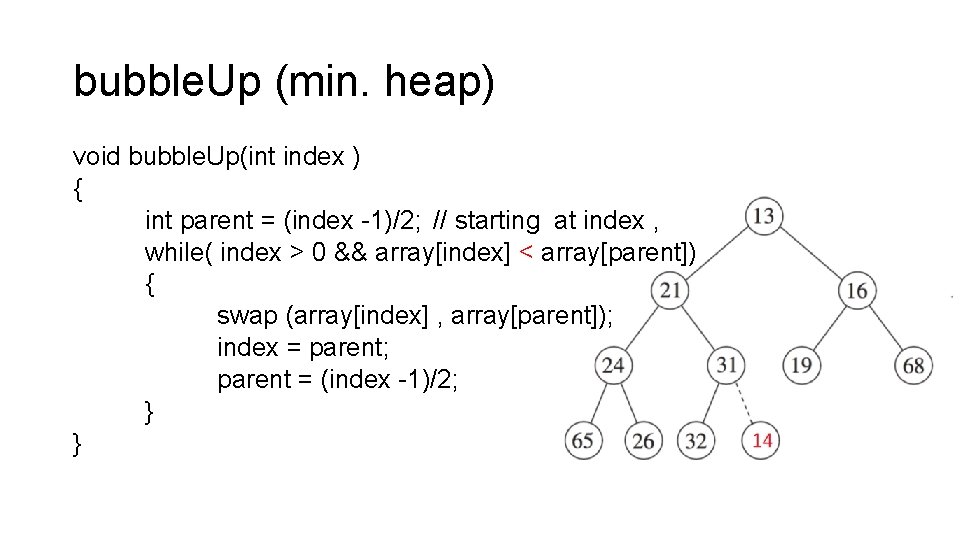
bubble. Up (min. heap) void bubble. Up(int index ) { int parent = (index -1)/2; // starting at index , while( index > 0 && array[index] < array[parent]) { swap (array[index] , array[parent]); index = parent; parent = (index -1)/2; } }

Time complexity of insertion in heap • Worst case of single insert: as much as O(log N) • Best case : O(1) • Average case : 2. 607 comparisons -> O(1) • Worst case of N inserts: as much as O(N*log N)

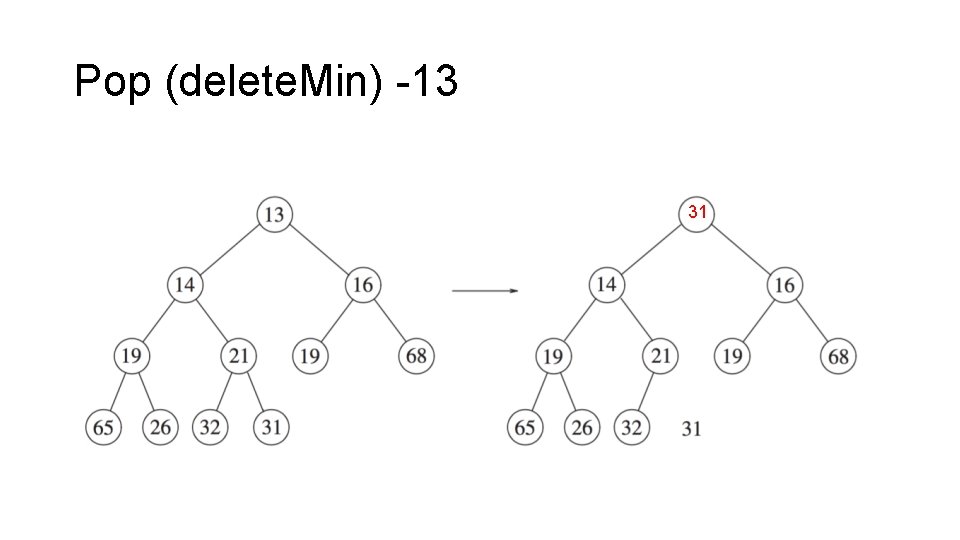
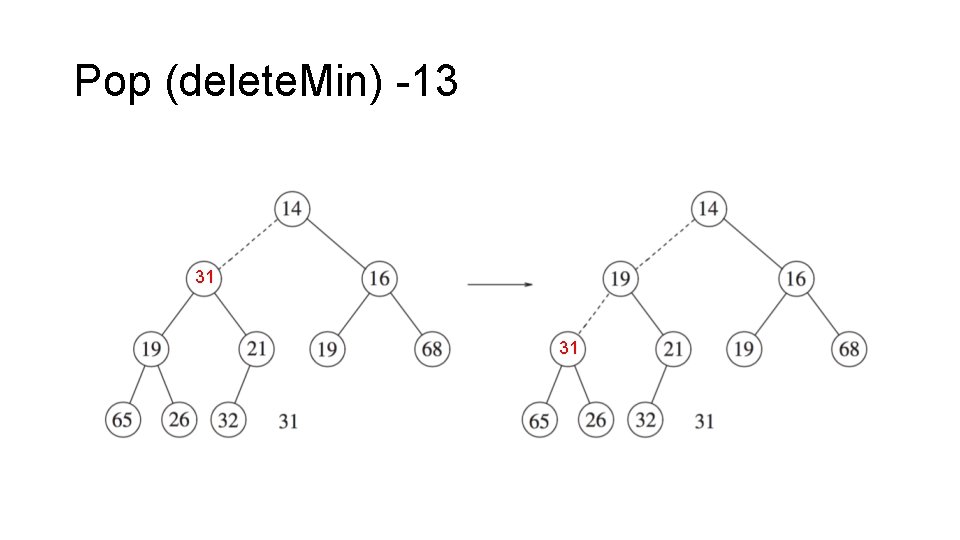
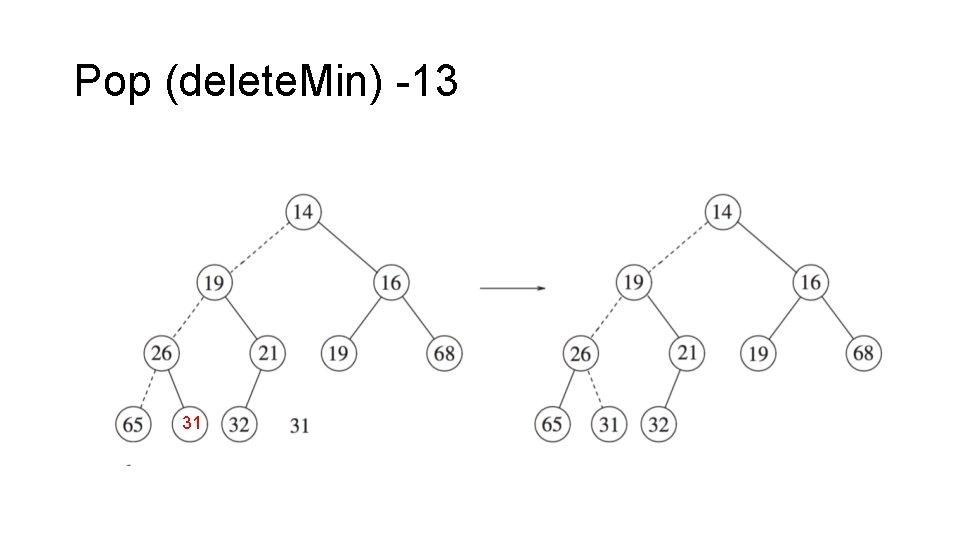
Pop • Top is easy, after pop , there is a “hole”at the root of the heap • When the minimum (or maximum) is removed, a hole is created at the root, swap the hole with the smaller of its children, thus pushing the hole down one level. 1) Overwrite 1 st item with the last item in the array 2) Bubble down ( percolate down )

Pop (delete. Min) -13 31

Pop (delete. Min) -13 31 31

Pop (delete. Min) -13 31

Pseudo code of bubble. Down (max. heap) void bubble. Down(int index ) { // while index is not at the last level // set child to node with the larger value // if index is smaller than child // swap index with child // else // done // update index and child }

Time complexity of bubble down • Worst case : as much as O(log N) • Average case : O(log N)

Heap is not a good choice when • Searching for random element (not minimum or maximum) • Finding an item which is not the highest priority

Build heap algorithm outline: 1) Take an (unsorted array) of values and assume that it's a complete binary tree -> Fulfils structure property requirement 2) Heapify : Call bubble. Down (percolate down) for each non-leaf node (starting at the lowest level) -> Fulfils heap-order property requirement

Two ways to build a heap • 1) Given N elements, build heap by N successive inserts Worst case -> O(N*log. N) • 2) Given N elements (assume) in a complete binary tree , What is the time complexity to turn the complete BT to a heap ? Is it possible to get better time complexity than O(N*log. N) ?

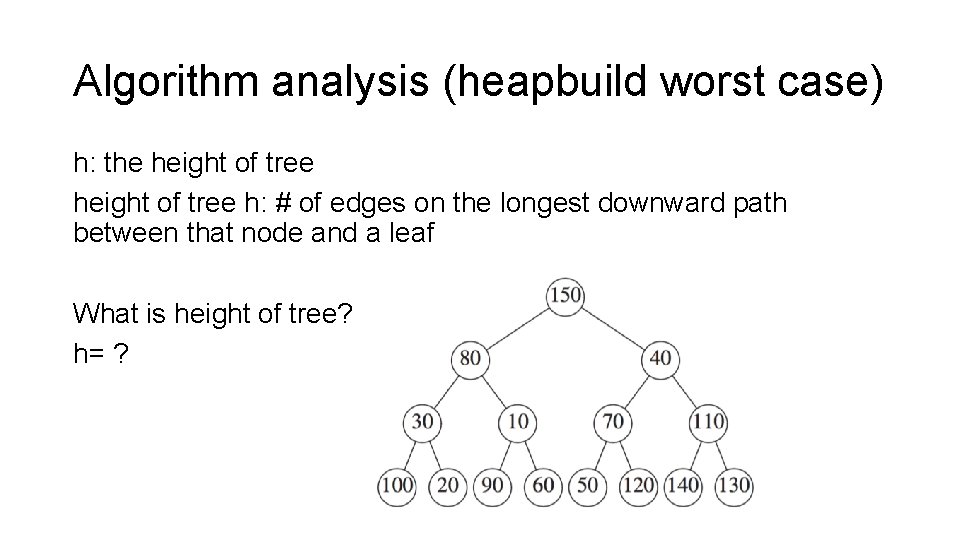
Algorithm analysis (heapbuild worst case) h: the height of tree h: # of edges on the longest downward path between that node and a leaf What is height of tree? h= ?

Observation from the binary tree Height (h) , # of bubble down ops. of each nodes Max Number of nodes at h 3=h 1 2=h-1 2 1=h-2 h-i …. . 22 2 i …. .

Ex. Summation of geometric sequence a 1=2 q=2

Ex. Summation of geometric sequence Sn=2(1 -2 n)/(1 -2)=2(2 h-1) a 1=2 q=2 S=-h+Sn=-h+2(2 h-1) and h=log. N S=-h+Sn=-h+2(2 h-1)=-log. N+2(2 log. N-1) after Canceling exponentials =log. N+2(N-1) , after ignoring lower order terms and constants =O(N)

Algorithm analysis (heapbuild worst case) • O(N) for worst-case and average-case • O(N) is better than O(N*log. N) in solution #1 , when N is large