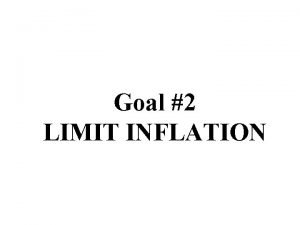Primordial NonGaussianities and QuasiSingle Field Inflation Xingang Chen

Primordial Non-Gaussianities and Quasi-Single Field Inflation Xingang Chen Center for Theoretical Cosmology, DAMTP, Cambridge University X. C. , 1002. 1416, a review on non-G; X. C. , Yi Wang, 0909. 0496; 0911. 3380

CMB and WMAP (WMAP website)

Temperature Fluctuations (WMAP website)

What sources these fluctuations?

CMB and WMAP (WMAP website)

Generic Predictions of Inflationary Scenario Density perturbations that seed the large scale struture are • Primordial (seeded at super-horizon size) • Approximately scale-invaraint • Approximately Gaussian

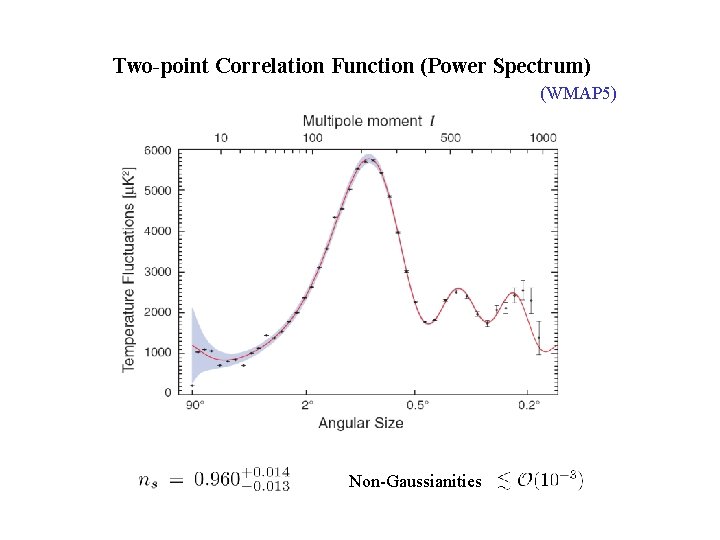
Two-point Correlation Function (Power Spectrum) (WMAP 5) Non-Gaussianities

Is this enough?

Experimentally: Information is Compressed • Amplitude and scale-dependence of the power spectrum (2 pt) contain 1000 numbers for WMAP • But we have pixels in WMAP temperature map This compression of information is justified only if the primordial fluctuations is perfectly Gaussian. Can learn much more from the non-Gaussian components.

Theoretically: From Paradigm to Explicit Models • What kind of fields drive the inflation? • What are the Lagrangian for these fields? • Alternative to inflation? • Quantum gravity

Non-G components: Primordial Interactions • Two-point correlation Free propagation of inflaton in inflationary bkgd • Three or higher-point correlations (non-Gaussianities) Interactions of inflatons or curvatons “LHC” for Early Universe!

What we knew theoretically about the non-Gaussianities

Simplest inflation models predict unobservable non-G. (Maldacena, 02; Acquaviva et al, 02) Ø Single field Ø Canonical kinetic term Ø Always slow-roll Ø Bunch-Davies vacuum Ø Einstein gravity Experimentally:

Inflation Model Building Examples of simplest slow-roll potentials: The other conditions in the no-go theorem also needs to be satisfied.

Much more complicated in realistic model building ……

Inflation Model Building A landscape of potentials

Inflation Model Building Warped Calabi-Yau

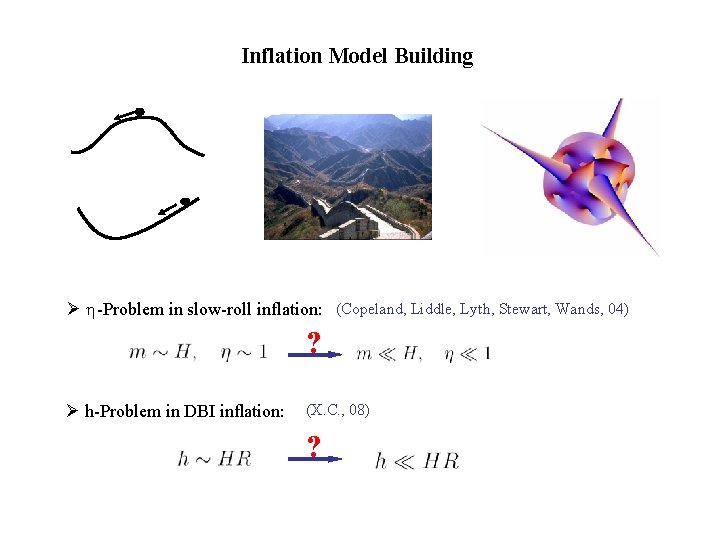
Inflation Model Building Ø h-Problem in slow-roll inflation: (Copeland, Liddle, Lyth, Stewart, Wands, 04) ? Ø h-Problem in DBI inflation: (X. C. , 08) ?

Ø Field range bound: (X. C. , Sarangi, Tye, Xu, 06; Baumann, Mc. Allsiter, 06) ? Ø Variation of potential: (Lyth, 97) : eg. higher dim Planck mass, string mass, warped scales etc.

Algebraic simplicity may not mean simplicity in nature.

Beyond the No-Go Ø Canonical kinetic term Non-canonical kinetic terms: DBI inflation, k-inflation, etc Ø Always slow-roll Features in potentials or Lagrangians: sharp, periodic, etc Ø Bunch-Davies vacuum Non-Bunch-Davies vacuum due to boundary condions, low new physics scales, etc Ø Single field Multi-field: turning trajectories, curvatons, inhomogeous reheating surface, etc Quasi-single field: massive isocurvatons

Shape and Running of Bispectra (3 pt) Bispectrum is a function, with magnitude • Shape dependence: (Shape of non-G) Fix Squeezed • Scale dependence: (Running of non-G) , vary Equilateral Fix , of three momenta: , , . Folded , vary .

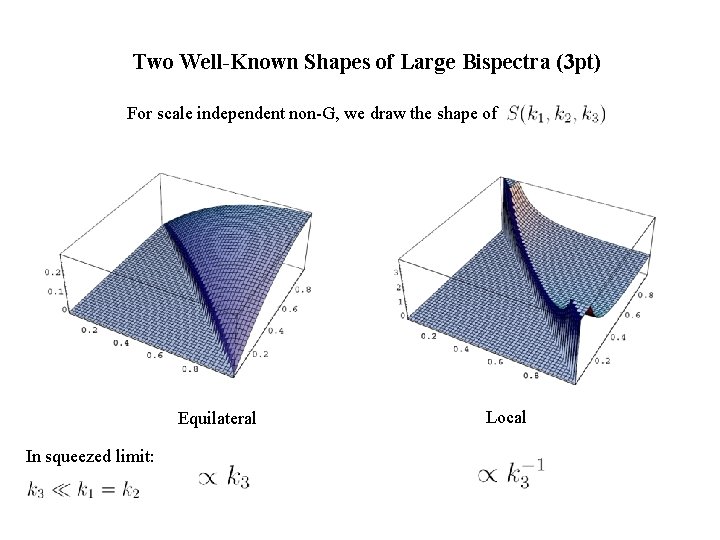
Two Well-Known Shapes of Large Bispectra (3 pt) For scale independent non-G, we draw the shape of Equilateral In squeezed limit: Local

Physics of Large Equilateral Shape • Generated by interacting modes during their horizon exit Quantum fluctuations Interacting and exiting horizon Frozen For single field, small correlation if So, the shape peaks at equilateral limit. • For example, in single field inflation with higher order derivative terms (Inflation dynamics is no longer slow-roll) (Alishahiha, Silverstein, Tong, 04; X. C. , Huang, Kachru, Shiu, 06)

Physics of Large Local Shape • Generated by modes after horizon exit, in multifield inflation Ø Isocurvature modes curvature mode Ø Patches that are separated by horizon evolve independently (locally) Local in position space non-local in momentum space So, the shape peaks at squeezed limit. • For example, in curvaton models; (Lyth, Ungarelli, Wands, 02) multifield inflation models with turning trajectory, (very difficult to get observable non. G. ) (Vernizzi, Wands, 06; Rigopoulos, Shellard, van Tent, 06)

What we knew experimentally about the non-Gaussianities

Experimental Results on Bispectra • WMAP 5 Data, 08 (Yadav, Wandelt, 07) (Rudjord et. al. , 09) (WMAP group, 10) ; • Large Scale Structure (Slosar et al, 08)

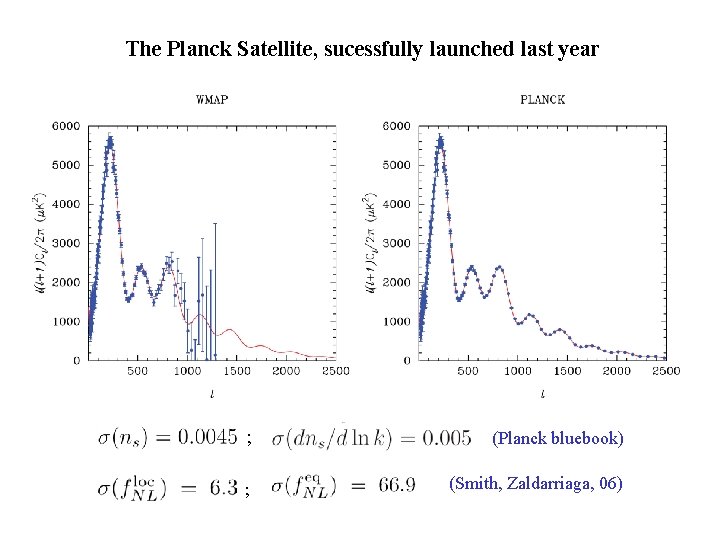
The Planck Satellite, sucessfully launched last year ; (Planck bluebook) ; (Smith, Zaldarriaga, 06)

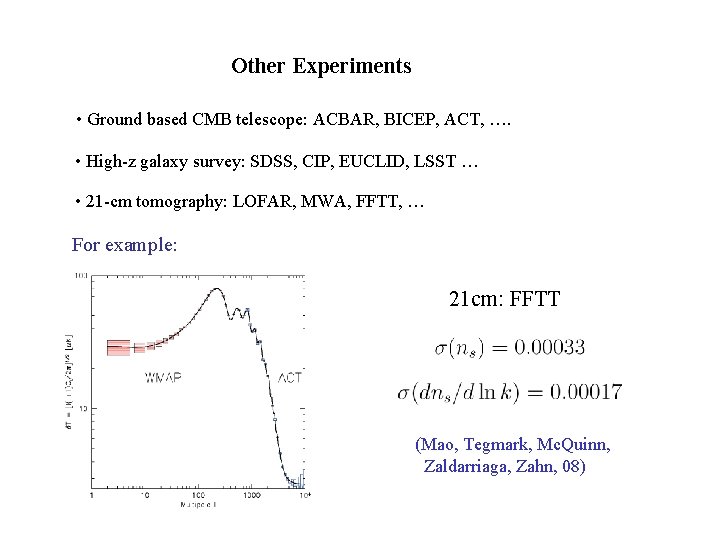
Other Experiments • Ground based CMB telescope: ACBAR, BICEP, ACT, …. • High-z galaxy survey: SDSS, CIP, EUCLID, LSST … • 21 -cm tomography: LOFAR, MWA, FFTT, … For example: 21 cm: FFTT (Mao, Tegmark, Mc. Quinn, Zaldarriaga, Zahn, 08)

Looking for Other Shapes and Runnings of Non-Gaussianities in Simple Models • Why? Underlying physics Different dynamics in inflation predict different non-G. Data analyses Theoretical template Construct estimator for example Fit data to constrain for example Ø So possible signals in data may not have been picked up, if we are not using the right theoretical models. Ø A positive detection with one ansatz does not mean that we have found the right form.

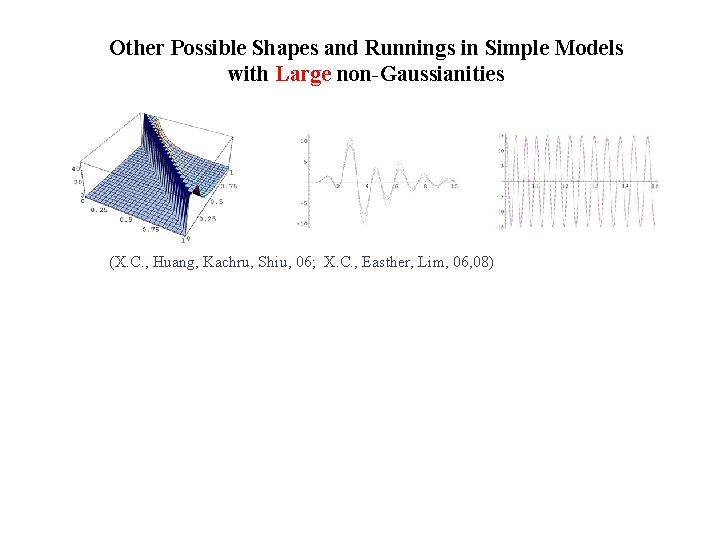
Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities (X. C. , Huang, Kachru, Shiu, 06; X. C. , Easther, Lim, 06, 08)

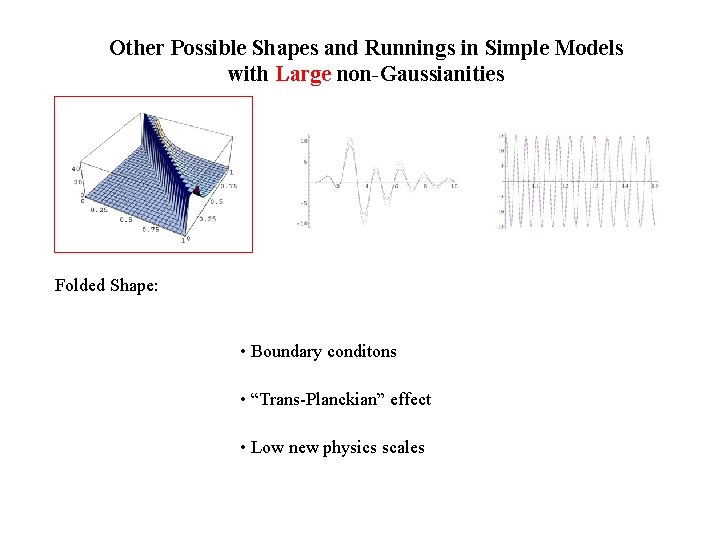
Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Folded Shape: (X. C. , Huang, Kachru, Shiu, 06; Meerburg, van de Schaar, Corasaniti, Jackson, 09) The Bunch-Davis vacuum: Non-Bunch-Davis vacuum: In 3 pt: For example, a small Peaks at folded triangle limit

Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Folded Shape: • Boundary conditons • “Trans-Planckian” effect • Low new physics scales

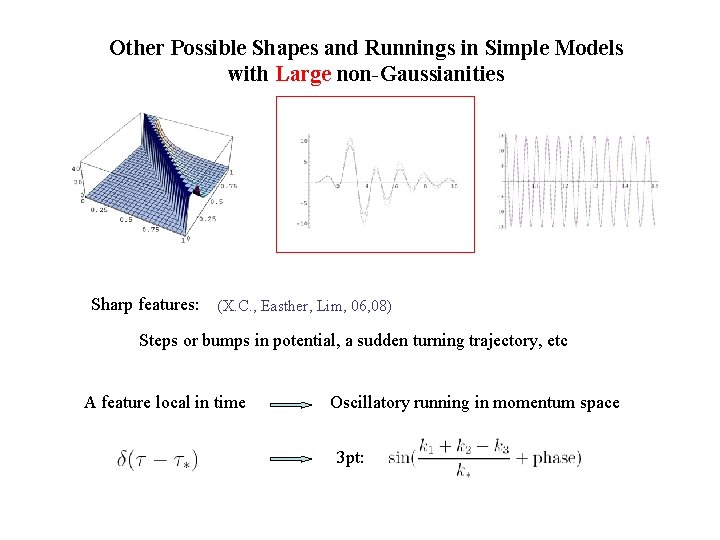
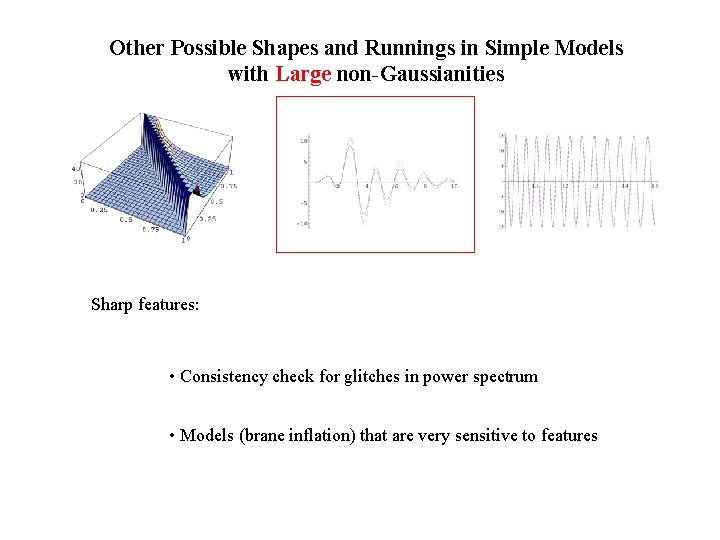
Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Sharp features: (X. C. , Easther, Lim, 06, 08) Steps or bumps in potential, a sudden turning trajectory, etc A feature local in time Oscillatory running in momentum space 3 pt:

Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Sharp features: • Consistency check for glitches in power spectrum • Models (brane inflation) that are very sensitive to features

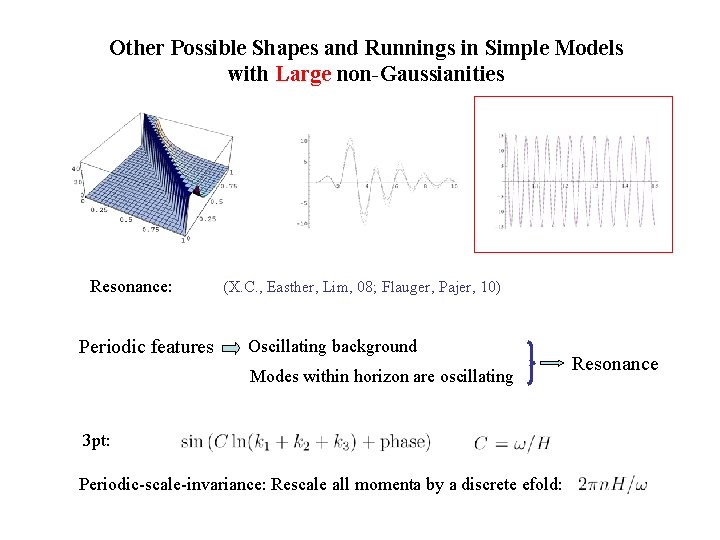
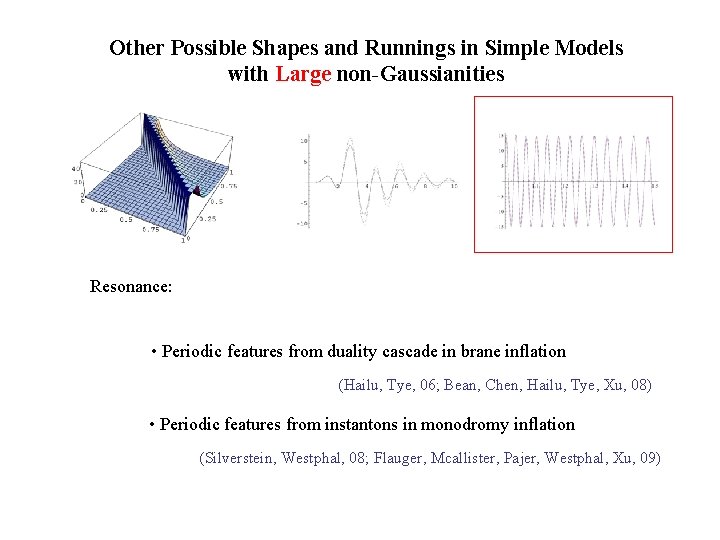
Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Resonance: Periodic features (X. C. , Easther, Lim, 08; Flauger, Pajer, 10) Oscillating background Modes within horizon are oscillating 3 pt: Periodic-scale-invariance: Rescale all momenta by a discrete efold: Resonance

Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities Resonance: • Periodic features from duality cascade in brane inflation (Hailu, Tye, 06; Bean, Chen, Hailu, Tye, Xu, 08) • Periodic features from instantons in monodromy inflation (Silverstein, Westphal, 08; Flauger, Mcallister, Pajer, Westphal, Xu, 09)

Other Possible Shapes and Runnings in Simple Models with Large non-Gaussianities (X. C. , Wang, 09)

Quasi-Single Field Inflation

Motivation for Quasi-Single Field Inflation • Fine-tuning problem in slow-roll inflation (Copeland, Liddle, Lyth, Stewart, Wands, 94) In the inflationary background, the mass of light particle is typically of order H (the Hubble parameter) E. g. C. f. is needed for slow-roll inflation • Generally, multiple light fields exist Ø One field has the mass Ø Others have mass Quasi-single field inflation (Ignored previously for den. pert. ) (X. C. , Wang, 09)

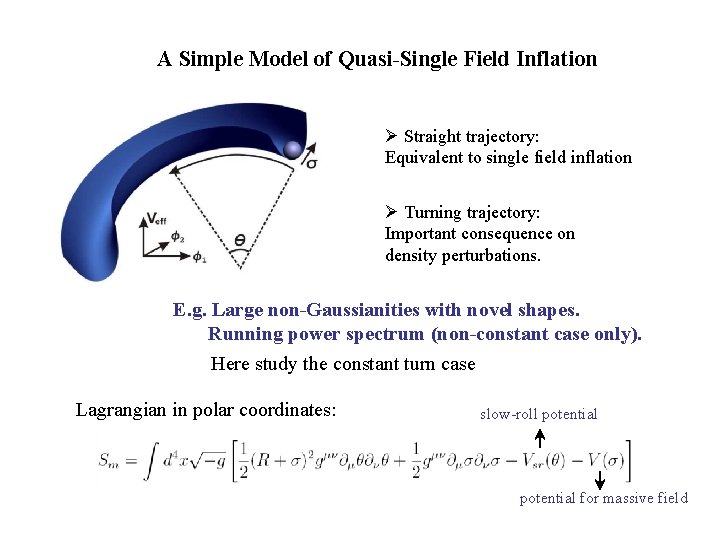
A Simple Model of Quasi-Single Field Inflation Ø Straight trajectory: Equivalent to single field inflation Ø Turning trajectory: Important consequence on density perturbations. E. g. Large non-Gaussianities with novel shapes. Running power spectrum (non-constant case only). Here study the constant turn case Lagrangian in polar coordinates: slow-roll potential for massive field

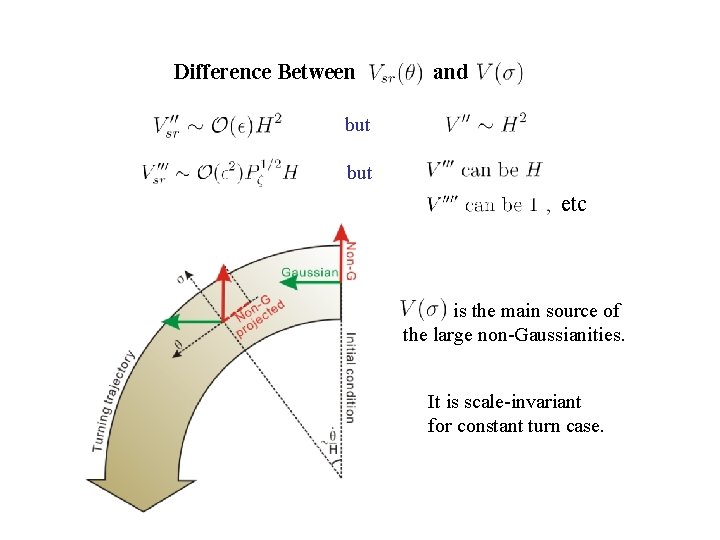
Difference Between and but etc is the main source of the large non-Gaussianities. It is scale-invariant for constant turn case.

Perturbation Theory • Field perturbations: • Lagrangian

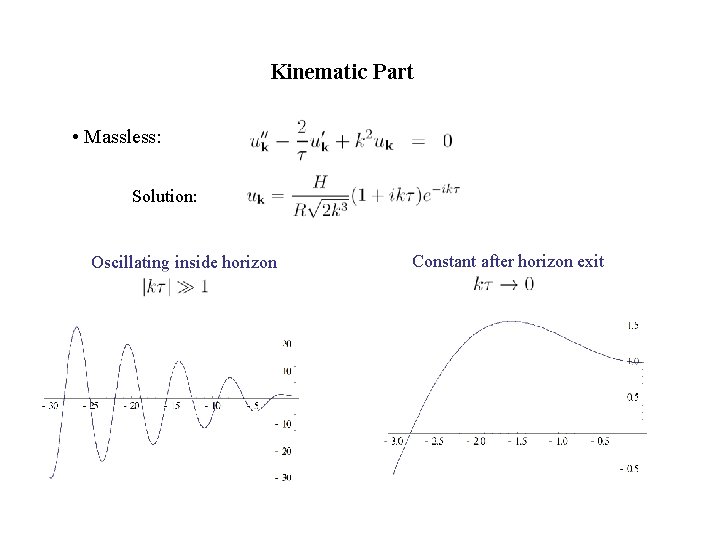
Kinematic Part • Massless: Solution: Oscillating inside horizon Constant after horizon exit

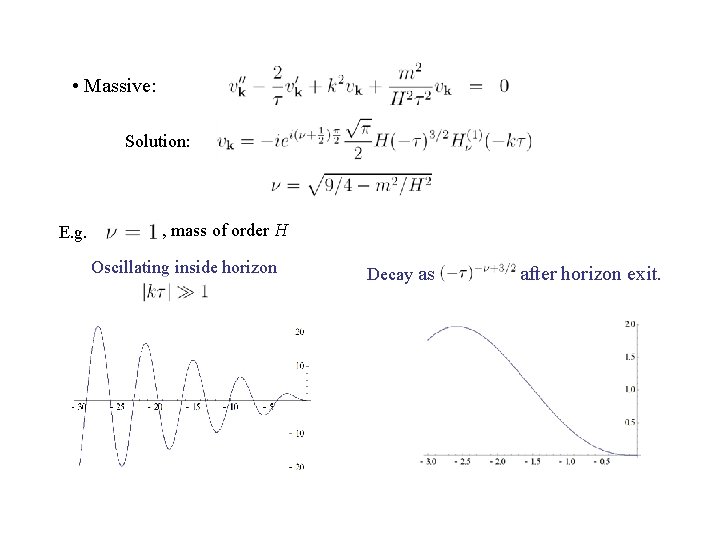
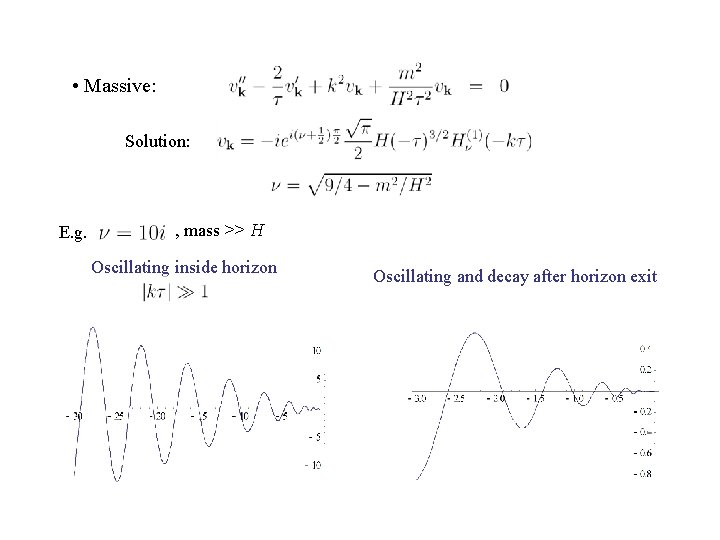
• Massive: Solution: E. g. , mass of order H Oscillating inside horizon Decay as after horizon exit.

• Massive: Solution: E. g. , mass >> H Oscillating inside horizon Oscillating and decay after horizon exit

• Massive: Solution: We will consider the case:

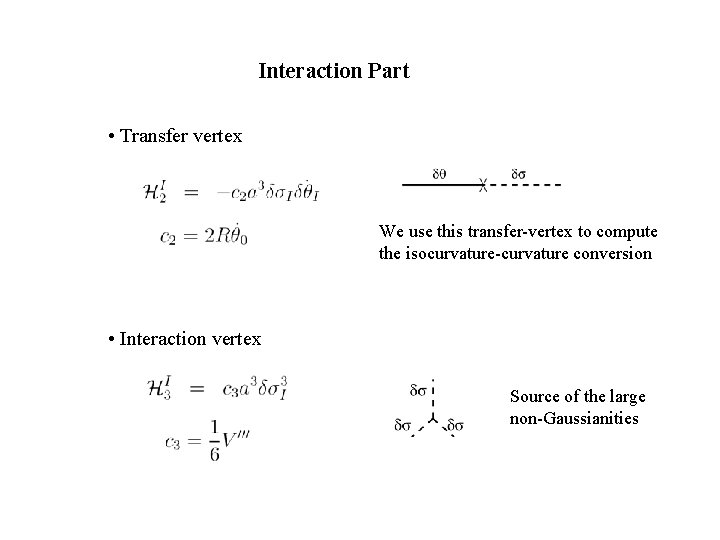
Interaction Part • Transfer vertex We use this transfer-vertex to compute the isocurvature-curvature conversion • Interaction vertex Source of the large non-Gaussianities

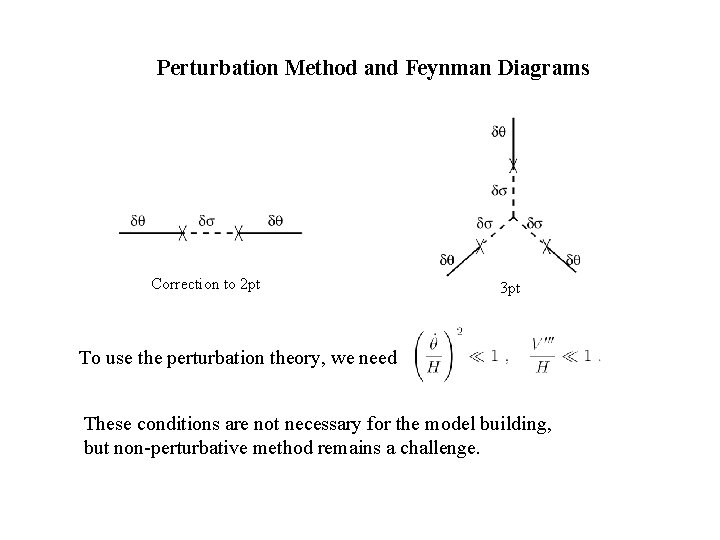
Perturbation Method and Feynman Diagrams Correction to 2 pt 3 pt To use the perturbation theory, we need These conditions are not necessary for the model building, but non-perturbative method remains a challenge.

In-In Formalism (Weinberg, 05) • Mixed form (X. C. , Wang, 09) Introduce a cutoff . “Factorized form” for UV part to avoid spurious UV divergence; “Commutator form” for IR part to avoid spurious IR divergence. Mixed form + Wick rotation for UV part A very efficient way to numerically integrate the 3 pt.

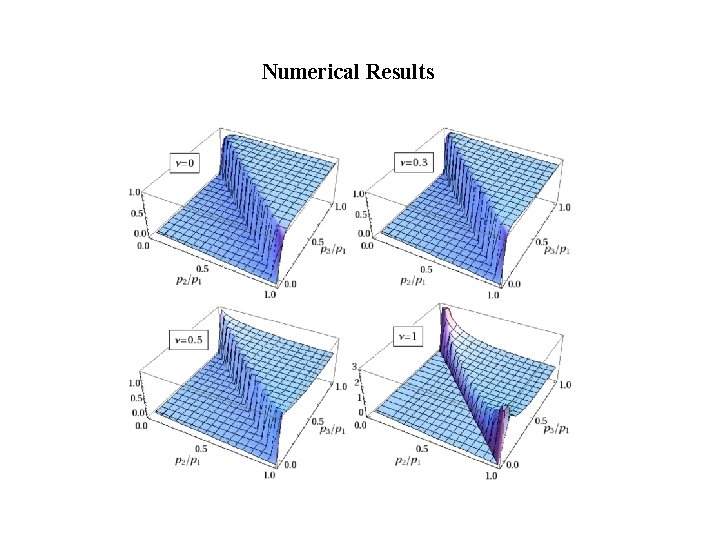
Numerical Results

Squeezed Limit and Intermediate Shapes Ø In squeezed limit, simple analytical expressions are possible. Ø Squeezed limit behavior also provide clues to guess a simple shape ansatz. Ø Can be used to classify shapes of non-G. • Using the asymptotic behavior of Hankel functions, we get the shape for • Lying between the equilateral form We call them Intermediate Shapes. , and local form (X. C. , Wang, 09) Not superposition of previously known shapes. .

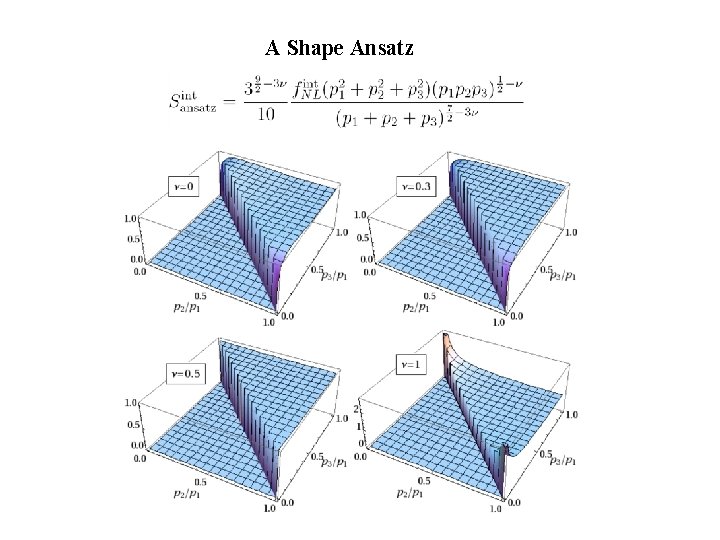
A Shape Ansatz

Compare Numerical Ansatz

Size of Bispectrum • Definition of : • We get For perturbative method: Non-perturbative case is also very interesting.

Physics of Large Intermediate Shapes • Quasi-equilateral: for heavier isocurvaton Fluctuations decay faster after horizon-exit, so large interactions happen during the horizon-exit. Modes have comparable wavelengths: Closer to equilateral shape. • Quasi-local: for lighter isocurvaton Fluctuations decay slower after horizon-exit, so non-G gets generated and transferred more locally in position space. In momentum space, modes become more non-local: Closer to local shape. In limit, recover the local shape behavior.

Effect of the Transfer Vertex A comparison of shapes before and after it is transferred • Before: Squeezed limit shape is , amplitude is decaying. • After: Shapes are changed during the transfer, slightly towards the local type. Important to investgate such effects in other models, including multi-field inflation.

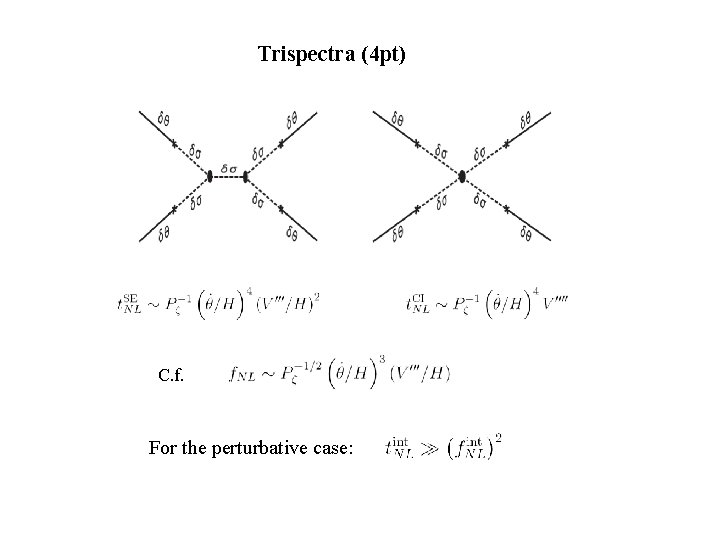
Trispectra (4 pt) C. f. For the perturbative case:

Conclusions • Using non-Gaussianities to probe early universe Different inflationary dynamics can imprint distinctive signatures in non-G; No matter whether non. G will turn out to be observable or not, detecting/constraining them requires a complete classification of their profiles.

Conclusions • Using non-Gaussianities to probe early universe Classification: • Higher derivative kinetic terms: Equilateral shape • Sharp feature: Sinusoidal running • Periodic features: Resonant running • A non-BD vacuum: Folded shape • Massive isocurvatons: Intermediate shapes • Massless isocurvaton: Local shape

Conclusions • Using non-Gaussianities to probe early universe Different inflationary dynamics can imprint distinctive signatures in non-G • Quasi-single field inflation Effects of massive modes on density perturbations • Transfer vertex in “in-in” formalism Compute isocurvature-curvature transition perturbatively • Non-Gaussianities with intermediate shapes Numerical, analytical and ansatz

Future Directions • Compare Intermediate Shapes, Resonant running, etc, with data and constrain and • Non-constant turn: running power spectrum and non. G • Build models from string theory, obtain natural values for parameters • More general concept of Quasi-Single Field Inflation: massive (H) fields – inflaton coupling can be more arbitrary • …. . .