Prediction of peak overlaps frequency in electropherograms using

Prediction of peak overlaps frequency in electropherograms using the independent doublets model 1 MCF 2007 DMITRY ANDREYEV, EDGAR ARRIAGA

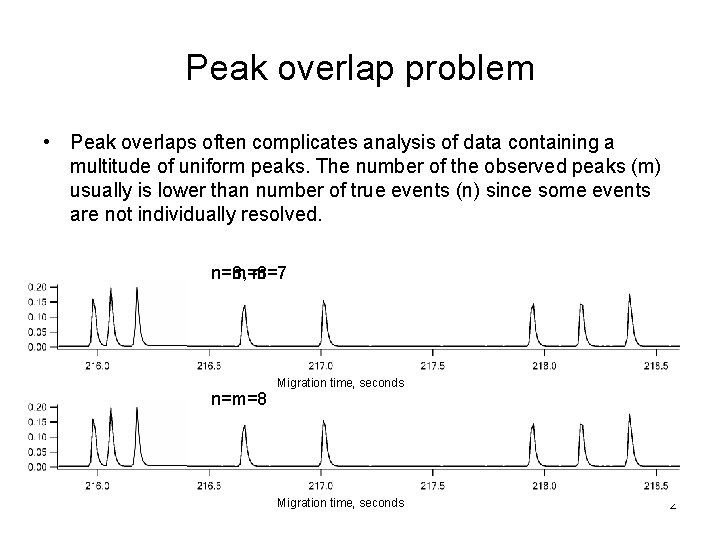
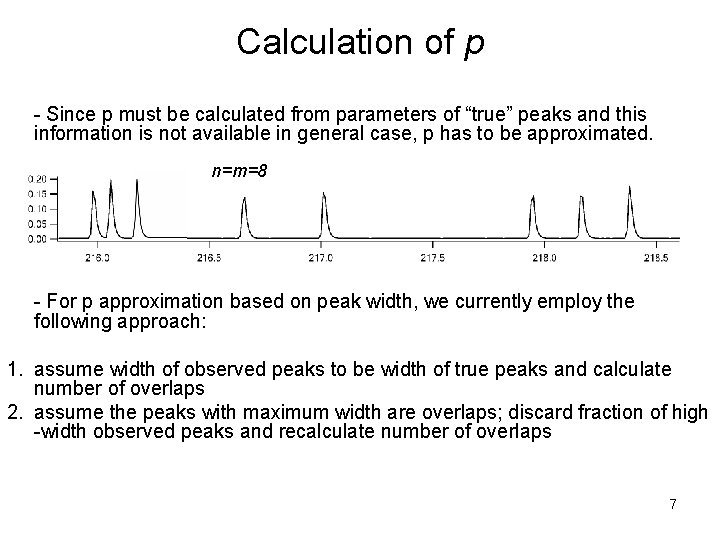
Peak overlap problem • Peak overlaps often complicates analysis of data containing a multitude of uniform peaks. The number of the observed peaks (m) usually is lower than number of true events (n) since some events are not individually resolved. n=m=8 n=8, m=7 n=m=8 Migration time, seconds 2

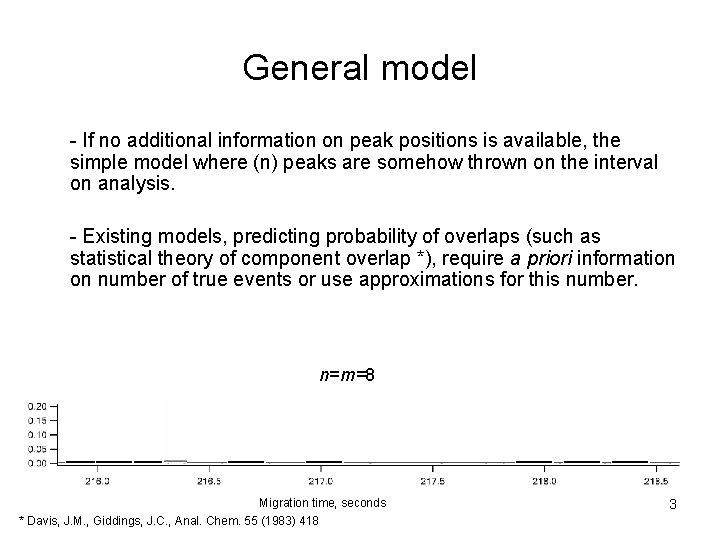
General model - If no additional information on peak positions is available, the simple model where (n) peaks are somehow thrown on the interval on analysis. - Existing models, predicting probability of overlaps (such as statistical theory of component overlap *), require a priori information on number of true events or use approximations for this number. n=m=8 Migration time, seconds * Davis, J. M. , Giddings, J. C. , Anal. Chem. 55 (1983) 418 3

Independent doublets model - Let N be a random variable, N=n if there are n “true” events. Let M be a random variable, M=m if there are m “observed” peaks. - Conditional probability of an event where {m peaks were observed} and {n true peaks were present} is P(M=m|N=n). - Assume the only kind of peak overlaps are doublets. - Let p be a probability of two given peaks produce a doublet. - Assume p is constant on the interval of analysis. There are possible peak pairs. There are ways to make n-m doublets among these possible pairs. Probability of n-m doublets are made from the particular peak pairs is and probability of all remaining pairs not made any doublets is . Hence, P(M=m|N=n) = 4

Independent doublets model - Maximum of P(M=m|N=n) = as function of n is the expected number of true events. - Is not trivial to find the maximum of P as a function of n analytically, but it can be found numerically. 5

Computer – friendly representation P(M=m|N=n) = = = = 6

Calculation of p - Since p must be calculated from parameters of “true” peaks and this information is not available in general case, p has to be approximated. n=m=8 - For p approximation based on peak width, we currently employ the following approach: 1. assume width of observed peaks to be width of true peaks and calculate number of overlaps 2. assume the peaks with maximum width are overlaps; discard fraction of high -width observed peaks and recalculate number of overlaps 7

8

Experimental validation Migration time, seconds Electropherogam (CE-LIF) of polystyrene microspheres (continuous injection, m = 450, time window 358 s, average peak width 50 ms, minimum spacing between maxima of non-overlapping peaks 50 ms). The calculated number of doublets (15) was found to be in good agreement with number of experimental overlaps (17), estimated from increase in peak height. In contrast, the statistical theory of component overlap predicted a significantly higher number of peak overlaps (54), when m is taken as a rough approximation of n. 9

Further considerations - The assumptions for the model (1. the only kind of peak overlaps are doublets; 2. p is constant on the interval of analysis) can introduce errors. - These errors have to be estimated. 10

For multiplets of higher orders n could be overestimated 1 2 3 • Let’s look on 3 peaks (1, 2, 3). • If peaks 1 -2 and 2 -3 overlaps -> we have two doublets -> model works OK. • But presence of these doublets affects probability, that peaks 1 -3 are overlaps too! • Let g be a probability that two peaks overlap, if each of them overlap with a third peak. Note: g >> p. 11

For multiplets of higher orders n could be overestimated • That is a full probability of such triple overlap? • There are potential triplets, each making a pair of overlaps with probability p 2. The third overlap is made with probability g. So, probability to overestimate n by 1 is: • For special cases (p × n is bid) this error can be significant and should be addressed by introduction of multiplets of higher orders into formula for P(M=m|N=n). 12

Intervals for analysis • In general, p does not stay constant over time of the experiment. • Small intervals can be analyzed instead of whole time in hope for local stability of p. • How small these intervals should be? Too small => not enough peaks for statistical significance; too big => p variations too high. • Currently, arbitrary visual analysis is employed for choosing the intervals. • To automate the process, the function of p variations can be represented as smoothed reciprocal of migration times, but the approach still needs to be validated. 13

Conclusion - New approach for prediction of peak overlap frequency is developed. - This approach does not require a priory knowledge or approximation of number of “true events”. - Theoretical calculations are in the good agreement with experiment. 14

Acknowledgments Edgar Arriaga and Arriaga’s group members; UMN Department of Chemistry and NIH for making this work possible. 15

16

Complications with doublet independence approach. Variations of p. • p obviously does not stay constant over time of the experiment. • Small intervals can be analyzed instead of whole time in hope for local stability of p. • How small these intervals should be? Too small => not enough peaks for statistical significance; too big => p variations too high. • Function of p variations as smoothed reciprocal of migration times? Visual analysis of histograms of p with varied bin width? Something else? 17

Encoding in Igor Pro • • • Function overlaps 3 D(): Button. Control variable k, l, p, m_min=10, m_max=60, p_min=0. 001, p_max=0. 1, p_res=10 make/o/d/n=( (m_max - m_min), p_res ) prob_wave for (l=0; l<=p_res ; l+=1) p=(p_max-p_min)*l/p_res for (k=m_min; k<=m_max ; k+=1) • • overlaps_core(p, k) wavestats /q wave_n • • • prob_wave[k, l]=V_maxloc endfor • endfor execute "Create. Surfer /N=probability_plot /K=1" execute "Modify. Surfer src. Wave=prob_wave src. Type=1" End 18

Peak overlap problem - existing approaches - Most widely used: Statistical theory of component overlap (by Davis and Giddings*) predicts number of “true” events as , where X is length of analyzed interval, is peak capacity and λ is density of true events. - requires a priori information about density of true events * Davis, J. M. , Giddings, J. C. , Anal. Chem. 55 (1983) 418

Statistical theory of component overlap (by Davis and Glddings). For “observed” peaks (m) and assuming λ (peak density) constant on on small intervals: For “true” peak number (p): Can we use this equation to calculate p? No, since we don’t know λ. 20

Complications with doublet independence approach. Calculation of p. • p must be calculated from parameters of “true” peaks and this information is not available. For p approximation based on peak width, one possible approach includes: • (i) discard of close peaks (peak width compromised in existing algorithm, for better one peak shape required and it is complex and not symmetrical in many our cases) • (ii) assume width of observed peaks to be width of true peaks and calculate number of overlaps • (iii) assume the peaks with maximum width are overlaps; discard fraction of high-width observed peaks and recalculate number of overlaps • (iiii) pray for convergence ☺ 21

Prediction of peak overlaps frequency in electropherograms using the independent doublets model Peak overlaps often complicates analysis of data containing a multitude of uniform peaks. For example, electropherograms of individual particles typically have 102 - 103 peaks in a 10 -min time window. The number of the observed peaks (m) usually is lower than number of true events (n) since some events are not individually resolved. The existing approaches to predict peak overlaps are not ideal. For example the Statistical Overlap Theory (SOT), requires a priori information about n. Here, we suggest a new and direct approach for prediction of the number of peak overlaps. The following assumptions are made: (i) the only kind of overlaps are doublets and (ii) the probability of two given peaks forming a doublet remains the same for any pair of events in a given time interval. Under these assumptions, P, the conditional probability of observing m peaks when n true events are present can be defined mathematically. Is not trivial to find the maximum of P as a function of n analytically, but it can be found numerically. The independent doublets model was applied to an electropherogam of polystyrene microspheres (m = 450, time window 358 s, average peak width 50 ms, minimum spacing between maxima of non-overlapping peaks 50 ms). The calculated number of doublets (15) was found to be in good agreement with number of experimental overlaps (17), estimated from increase in peak height. In contrast, the SOT predicted a significantly higher number of peak overlaps (54), when m is taken as an approximation of n.

Independent doublets model P(M=m|N=n) = P(m, n)=( p, n); but P(m, n)= ? ; Is not trivial to find the maximum of P as a function of n analytically, but it can be found numerically. 23