POLYNOMIAL FUNCTIONS A POLYNOMIAL is a monomial or

POLYNOMIAL FUNCTIONS A POLYNOMIAL is a monomial or a sum of monomials. A POLYNOMIAL IN ONE VARIABLE is a polynomial that contains only one variable. Example: 5 x 2 + 3 x - 7

POLYNOMIAL FUNCTIONS The DEGREE of a polynomial in one variable is the greatest exponent of its variable. A LEADING COEFFICIENT is the coefficient of the term with the highest degree. What is the degree and leading coefficient of 3 x 5 – 3 x + 2 ?

Remember integers are … – 2, -1, 0, 1, 2 … (no decimals or fractions) so positive integers would be 0, 1, 2 … A polynomial function is a function of the form: n must be a positive integer All of these coefficients are real numbers The degree of the polynomial is the largest power on any x term in the polynomial.

Polynomial Functions • Exponents must be non-negative integer exponents • Can not have variables in the denominator • Can not have radicals – Example: square root or cube root – These are actually fractional exponents

Determine which of the following are polynomial functions. If the function is a polynomial, state its degree. A polynomial of degree 4. We can write in an x 0 since this = 1. x 0 A polynomial of degree 0. Not a polynomial because of the square root since the power is NOT an integer Not a polynomial because of the x in the denominator since the power is negative

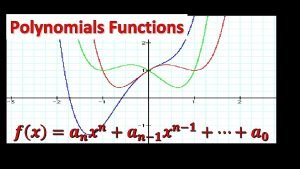
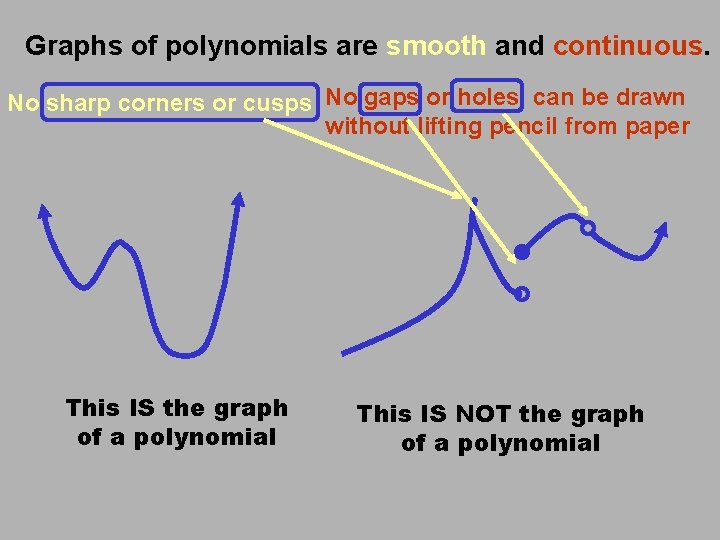
Graphs of polynomials are smooth and continuous. No sharp corners or cusps No gaps or holes, can be drawn without lifting pencil from paper This IS the graph of a polynomial This IS NOT the graph of a polynomial

POLYNOMIAL FUNCTIONS A polynomial equation used to represent a function is called a POLYNOMIAL FUNCTION. Polynomial functions with a degree of 1 are called LINEAR POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 2 are called QUADRATIC POLYNOMIAL FUNCTIONS Polynomial functions with a degree of 3 are called CUBIC POLYNOMIAL FUNCTIONS

POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = 3 Constant Function Degree = 0 Max. Zeros: 0

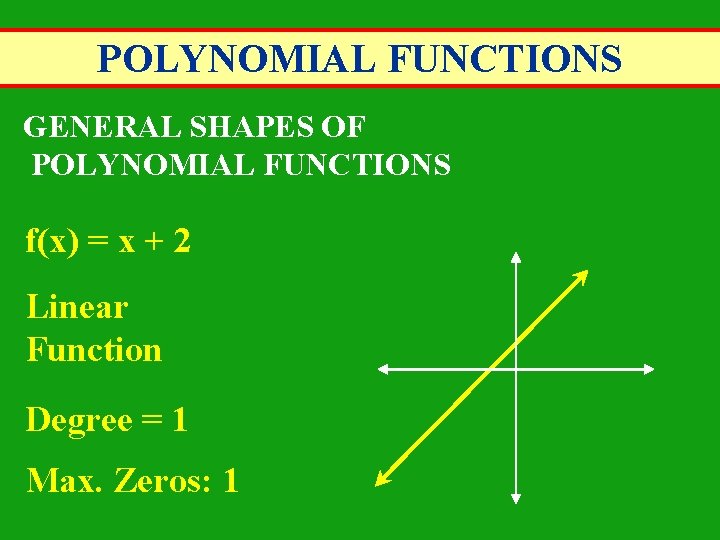
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x + 2 Linear Function Degree = 1 Max. Zeros: 1

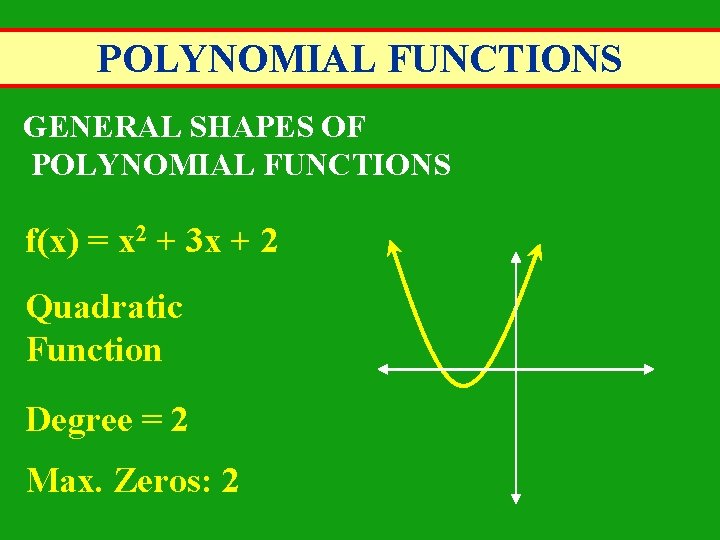
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 2 + 3 x + 2 Quadratic Function Degree = 2 Max. Zeros: 2

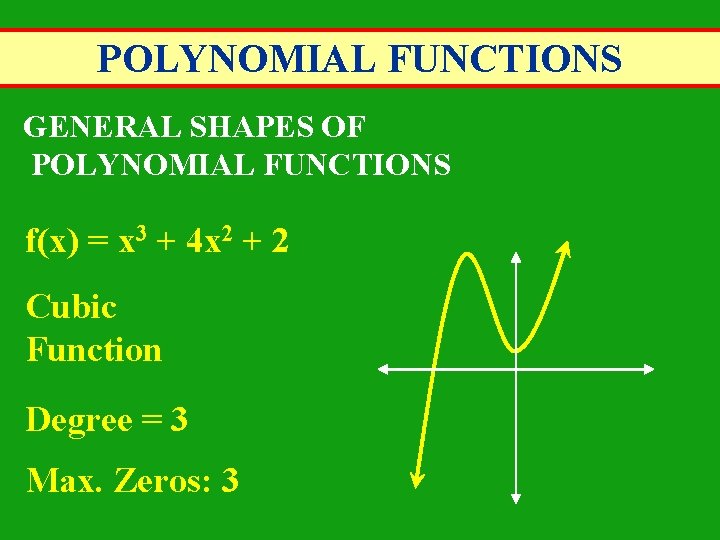
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 3 + 4 x 2 + 2 Cubic Function Degree = 3 Max. Zeros: 3

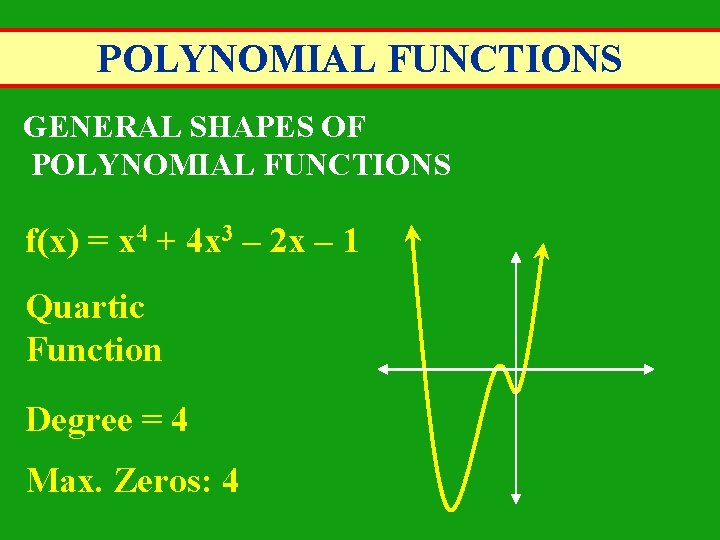
POLYNOMIAL FUNCTIONS GENERAL SHAPES OF POLYNOMIAL FUNCTIONS f(x) = x 4 + 4 x 3 – 2 x – 1 Quartic Function Degree = 4 Max. Zeros: 4

LEFT and RIGHT HAND BEHAVIOUR OF A GRAPH The degree of the polynomial along with the sign of the coefficient of the term with the highest power will tell us about the left and right hand behaviour of a graph.

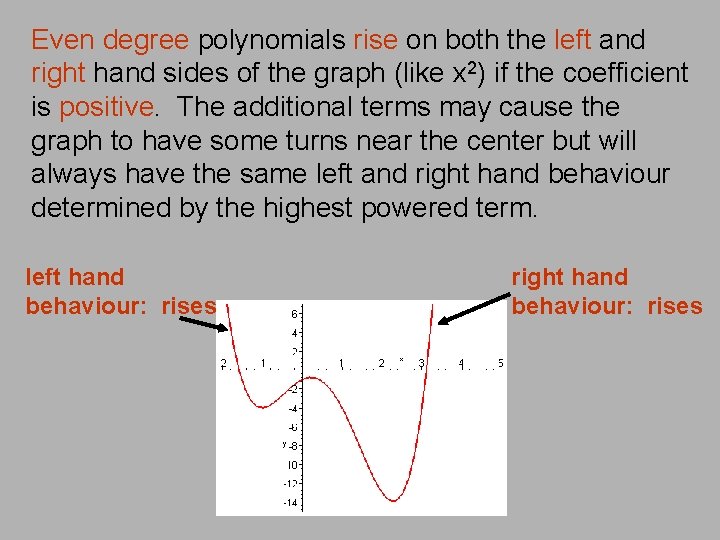
Even degree polynomials rise on both the left and right hand sides of the graph (like x 2) if the coefficient is positive. The additional terms may cause the graph to have some turns near the center but will always have the same left and right hand behaviour determined by the highest powered term. left hand behaviour: rises right hand behaviour: rises

Even degree polynomials fall on both the left and right hand sides of the graph (like - x 2) if the coefficient is negative. turning points in the middle left hand behaviour: falls right hand behaviour: falls

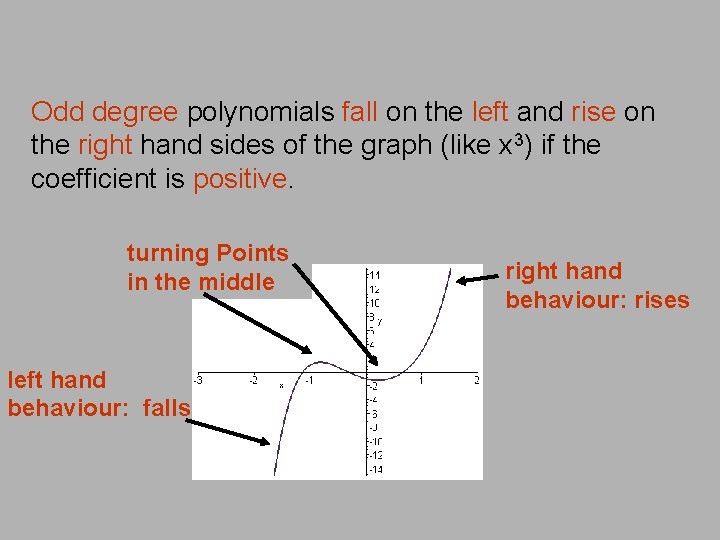
Odd degree polynomials fall on the left and rise on the right hand sides of the graph (like x 3) if the coefficient is positive. turning Points in the middle left hand behaviour: falls right hand behaviour: rises

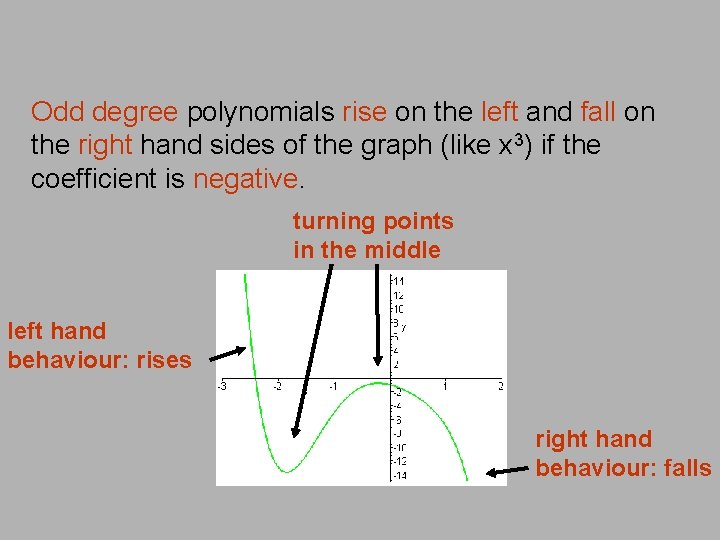
Odd degree polynomials rise on the left and fall on the right hand sides of the graph (like x 3) if the coefficient is negative. turning points in the middle left hand behaviour: rises right hand behaviour: falls

A polynomial of degree n can have at most n-1 turning points (so whatever the degree is, subtract 1 to get the most times the graph could turn). Let’s determine left and right hand behaviour for the graph of the function: doesn’t mean it has that many turning points but that’s the most it can have degree is 4 which is even and the coefficient is positive so the graph will look like x 2 looks off to the left and off to the right. The graph can have at most 3 turning points How do we determine what it looks like near the middle?

Characteristics • Maximum number of turns in 1 less than the degree • Degree – Odd with positive leading coefficient • Starts down and comes up – Even with positive leading coefficient • Starts up and comes down • Negative leading coefficient changes direction of starting position

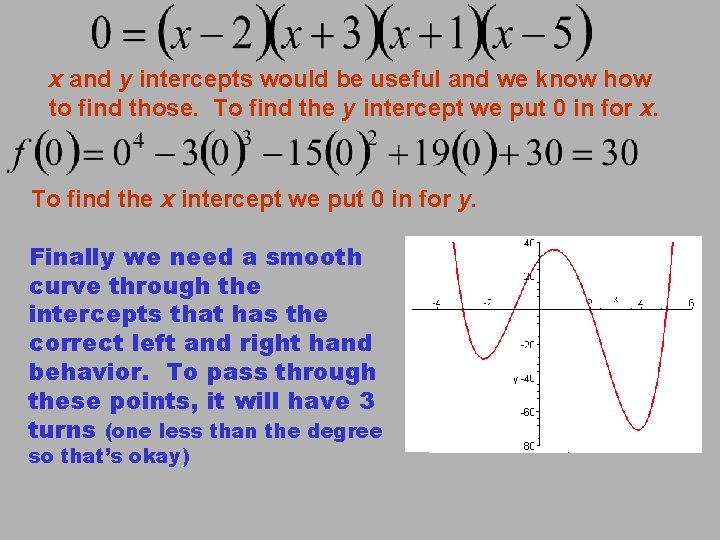
x and y intercepts would be useful and we know how to find those. To find the y intercept we put 0 in for x. To find the x intercept we put 0 in for y. Finally we need a smooth curve through the intercepts that has the correct left and right hand behavior. To pass through these points, it will have 3 turns (one less than the degree so that’s okay) (0, 30)