PLANOS Y SUPERFICIES U D 12 Angel Prieto

PLANOS Y SUPERFICIES U. D. 12 * @ Angel Prieto Benito 2º BCT Matemáticas 2º Bachillerato C. T. 1

SUPERFICIE ESFÉRICA U. D. 12. 4 @ Angel Prieto Benito * 2º BCT Matemáticas 2º Bachillerato C. T. 2

SUPERFICIES DEL ESPACIO • • Se llama superficie del espacio al conjunto de puntos P(f(s, t), g(s, t), h(s, t)) que se obtienen dando todos los valores posibles a s y t, siendo f(s, t), g(s, t) y h(s, t) funciones continuas. Z Las funciones: x = f(s, t) y = g(s, t) Y z = h(s, t) reciben el nombre de ecuaciones X paramétricas de la superficie, donde s y t son los parámetros. • • En el caso particular de que f(s, t), g(s, t) y h(s, t) sean funciones de la forma a + b. t + c. s, P(f(s, t), g(s, t), h(s, t)) representa un plano. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 3

Ejemplo • Sea el plano que pasa por el punto A(2 , – 1, 3) y sus vectores directores son u=(– 1, 3, 2) y v=(3, – 2 , 0). Hallar su ecuación paramétrica y define las funciones f(s, t), g(s, t) y h(s, t) que identifican dicho plano con una superficie del espacio. • • • Z Y X @ Angel Prieto Benito • Solución (x, y, z) = (2, – 1, 3) + t. (– 1, 3, 2) + s. (3, – 2, 0) es su ecuación vectorial. Las funciones que la definen como una curva en el espacio son: En paramétricas: • • • x = 2 – t + 3. s y = – 1 + 3. t – 2. s z = 3 + 2. t Matemáticas 2º Bachillerato C. T. f(s, t) = 2 – t + 3. s g(s, t) = – 1 + 3. t – 2. s h(s, t) = 3 + 2. t 4

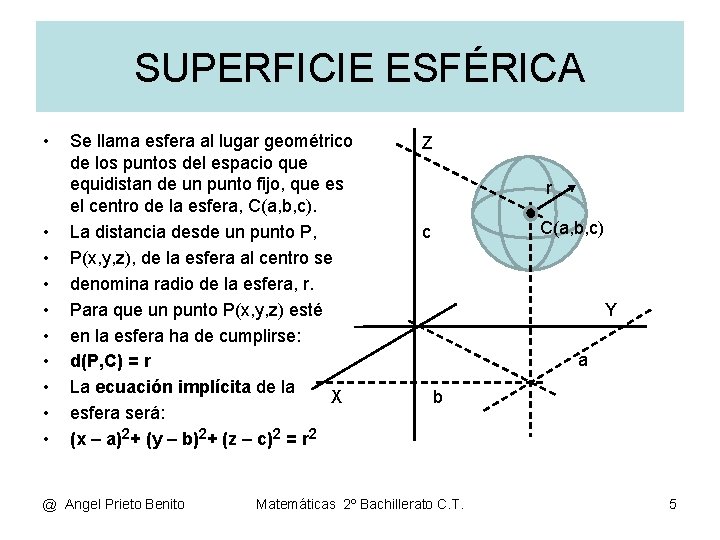
SUPERFICIE ESFÉRICA • • • Se llama esfera al lugar geométrico de los puntos del espacio que equidistan de un punto fijo, que es el centro de la esfera, C(a, b, c). La distancia desde un punto P, P(x, y, z), de la esfera al centro se denomina radio de la esfera, r. Para que un punto P(x, y, z) esté en la esfera ha de cumplirse: d(P, C) = r La ecuación implícita de la X esfera será: (x – a)2+ (y – b)2+ (z – c)2 = r 2 @ Angel Prieto Benito Z r C(a, b, c) c Y a b Matemáticas 2º Bachillerato C. T. 5

Centro y radio de la esfera • • • La ecuación implícita de la esfera será: (x – a)2+ (y – b)2+ (z – c)2 = r 2 Desarrollando la ecuación: x 2 + y 2 + z 2 – 2. a. x – 2. b. y – 2. c. z + a 2 + b 2 + c 2 = r 2 • • DEDUCCIÓN DEL CENTRO Y RADIO DE UNA ESFERA Si nos dan la ecuación desarrollada de la esfera: A. x 2 + A. y 2 + A. z 2 + B. x + C. y + D. z + E = 0 x 2 + y 2 + z 2 + (B/A). x + (C/A). y + (D/A). z + (E/A) = 0 , si A<>1 Podemos deducir el centro y el radio comparando términos semejantes. – 2. a = B/A a = – B/2. A – 2. b = C/A b = – C/2. A – 2. c = D/A c = – D/2. A • • a 2 + b 2 + c 2 – r 2 = E/A r = √(a 2+b 2+c 2–E/A)=√(B 2+C 2+D 2– 4. A. E) / 2. A Si el discriminante es negativo la esfera no es real. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 6

Ejercicios • Halla la ecuación de la esfera que tiene por centro y radio: • • 1º. - C(0, 1, 1), r=4 Operando queda: C: x 2 + (y – 1)2 + (z – 1)2 – 42 = 0 C: x 2 + y 2 + z 2 – 2 y – 2 z – 14 = 0 • • 2º. - C(-1, 0, 0), r=3 Operando queda: C: (x +1)2 + y 2 + z 2 – 32 = 0 C: x 2 + y 2 + z 2 + 2 x – 8 = 0 • • 3º. - C(2, -1), r=1 C: (x – 2)2 + (y + 2)2 + (z + 1)2– 12 = 0 Operando queda: C: x 2 + y 2 + z 2– 4 x + 4 y + 2 z + 8 = 0 • • 4º. - C(-7, -5, 3), r=2 C: (x +7)2 + (y + 5)2 + (z – 3)2– 22 = 0 Operando queda: C: x 2 + y 2 + z 2 + 14 x + 10 y – 6 z + 79 = 0 • • 5º. - C(k, 0, k), r=k Operando queda: @ Angel Prieto Benito C: (x – k)2 + y 2 + (z – k)2 – k 2 = 0 C: x 2 + y 2 + z 2 – 2. k. x – 2. k. z + k 2 = 0 Apuntes 1º Bachillerato CT 7

Ejercicios • Halla el centro C(a, b, c) y radio r de las circunferencias: • • 1º. - C: x 2 + y 2 + z 2 + 2 y – 8 = 0 b 2 – r 2 = - 8 1 – r 2 = – 8 a = c = 0 2 b = - 2 b = -1 r 2 = 9 r = 3 • • 2º. - C: x 2 + y 2 + z 2– 6 x + 9 = 0 a 2 – r 2 = 9 9 – r 2 = 9 b = c = 0 2 a = 6 a = 3 r 2 = 0 r = 0 No hay • • 3º. - C: x 2 + y 2 + z 2– 4 y = 0 b 2 – r 2 = 0 4 – r 2 = 0 a = c = 0 2 b = 4 b = 2 r 2 = 4 r = 2 • • 4º. - C: x 2 + y 2 + z 2 – 4 y + 2 z + 9 = 0 b 2 + c 2 – r 2 = 9 1 + 4 – r 2 = 9 a = 0, c = – 1, b = 2 r 2 = – 4 r = No es real • • 4º. - C: x 2 + y 2 + z 2 + 2 x – 4 y – 4 = 0 a 2 + b 2 – r 2 = – 4 1 + 4 – r 2 = – 4 a=– 1, b=2, c=0 r 2 = 9 r = 3 @ Angel Prieto Benito Apuntes 1º Bachillerato CT 8

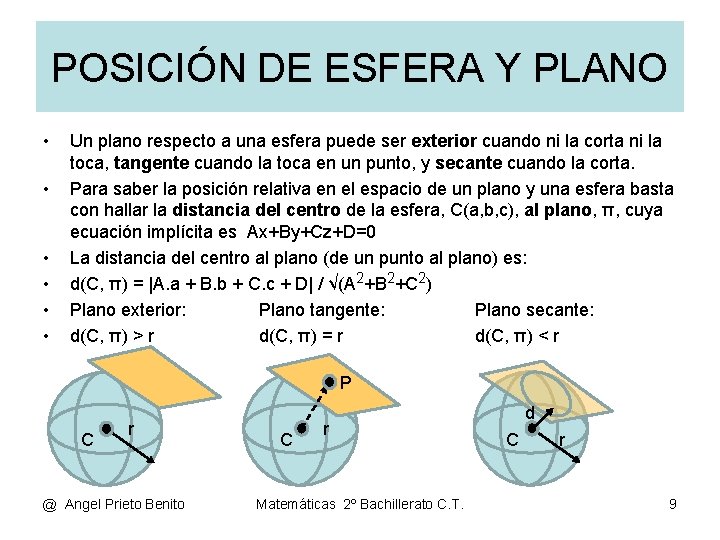
POSICIÓN DE ESFERA Y PLANO • • • Un plano respecto a una esfera puede ser exterior cuando ni la corta ni la toca, tangente cuando la toca en un punto, y secante cuando la corta. Para saber la posición relativa en el espacio de un plano y una esfera basta con hallar la distancia del centro de la esfera, C(a, b, c), al plano, π, cuya ecuación implícita es Ax+By+Cz+D=0 La distancia del centro al plano (de un punto al plano) es: d(C, π) = |A. a + B. b + C. c + D| / √(A 2+B 2+C 2) Plano exterior: Plano tangente: Plano secante: d(C, π) > r d(C, π) = r d(C, π) < r P C r @ Angel Prieto Benito C r Matemáticas 2º Bachillerato C. T. d C r 9

Ejercicios • • • Estudiar la posición relativa de un plano (exterior, tangente o secante) con respecto a la esfera de ecuación: (x – 2)2+(y + 3)2+(z – 1)2 = 25 Ejercicio 1: Siendo el plano π: 8. x – 6. z + 7 = 0 La distancia del centro, C(2 , – 3 , 1) al plano: d(C, π) = |A. a + B. b + C. c + D| / √(A 2+B 2+C 2) d(C, π) = |8. 2 + 0. (-3) + (-6). 1 + 7| / √(82+02+(-6)2) = 17 / 10 = 1, 70 Plano secante, pues d(C, π) < r 1, 70 < 5 • • • Ejercicio 2: Siendo el plano π: 3 x + 4 y – 12. z + 96 = 0 La distancia del centro, C(2 , – 3 , 1) al plano: d(C, π) = |A. a + B. b + C. c + D| / √(A 2+B 2+C 2) d(C, π) = |3. 2 + 4. (-3) + (-12). 1 + 96| / √(32+42+(-12)2) = 78 / 13 = 6 Plano exterior, pues d(C, π) > r 6 > 5 @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 10

Ejercicios • • • Estudiar la posición relativa de un plano (exterior, tangente o secante) con respecto a la esfera de ecuación: (x – 2)2+(y + 3)2+(z – 1)2 = 25 Ejercicio 3: Siendo el plano π: 8. x + 6. y – 48 = 0 La distancia del centro, C(2 , – 3 , 1) al plano: d(C, π) = |A. a + B. b + C. c + D| / √(A 2+B 2+C 2) d(C, π) = |8. 2 + 6. (-3) + 0. 1 – 48| / √(82+62+02) = 50 / 10 = 5 Plano tangente, pues d(C, π) = r 5 = 5 Ejercicio 4: Hallar k para que el plano π: x – y + k. z = 0 sea tangente a la mencionada esfera de centro, C(2 , – 3 , 1). d(C, π) = |A. a + B. b + C. c + D| / √(A 2+B 2+C 2) = r |1. 2 + (-3). (-1) + 1. k| / √(12+(-1)2+k 2) = 5 (k+5) /(√(2+k 2) = 5 k 2 + 10. k + 25 = 25. (2+ k 2) 24. k 2 – 10. k + 25 = 0 Discriminante = 100 – 2400 < 0 No hay ningún valor real de k. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 11

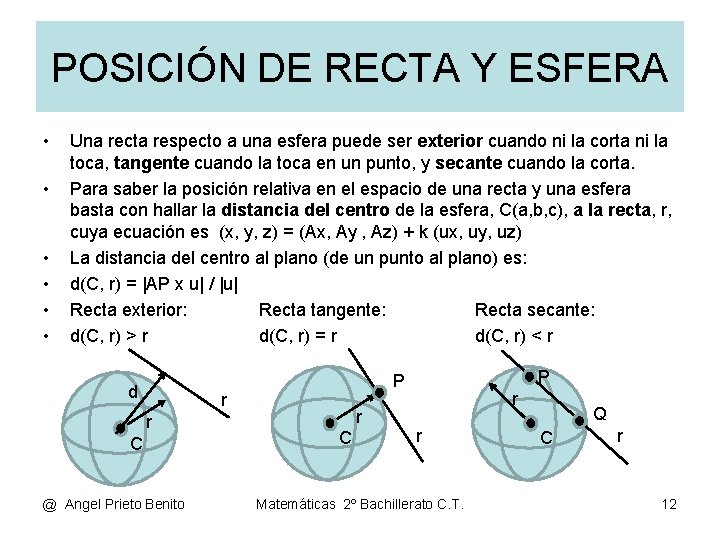
POSICIÓN DE RECTA Y ESFERA • • • Una recta respecto a una esfera puede ser exterior cuando ni la corta ni la toca, tangente cuando la toca en un punto, y secante cuando la corta. Para saber la posición relativa en el espacio de una recta y una esfera basta con hallar la distancia del centro de la esfera, C(a, b, c), a la recta, r, cuya ecuación es (x, y, z) = (Ax, Ay , Az) + k (ux, uy, uz) La distancia del centro al plano (de un punto al plano) es: d(C, r) = |AP x u| / |u| Recta exterior: Recta tangente: Recta secante: d(C, r) > r d(C, r) = r d(C, r) < r d r r C @ Angel Prieto Benito P P r C r r Matemáticas 2º Bachillerato C. T. Q C r 12

Ejercicios • • • • @ Estudiar la posición relativa de una recta (exterior, tangente o secante) con respecto a la esfera de ecuación: (x – 2)2+(y + 3)2+(z – 1)2 = 25 Ejercicio 1: Siendo la recta r: (x, y, z) = (1, 1, 1) + k(1 , – 1 , 1) La distancia del centro, C(2 , – 3 , 1) a la recta es: i j k d(C, r) = |AC x u| / |u| = 2 -1 -3 -1 1 -1 / √(12+(-1)2+12) = 1 -1 1 =|-4 i-k+4 k-j| / √ 3 = |-4 i-j + 3 k| / √ 3 = √(16+1+9) / √ 3 = 5 / √ 3 Recta secante pues d(C, r) < r (5 /√ 3) < 5 Hallemos los puntos de corte de recta y esfera: En la recta: x = 1 + k , y = 1 – k , z = 1 + k En la esfera: (1 + k – 2)2+(1 – k + 3)2+(1 + k – 1)2 = 25 Operando: k 2 + k 2 – 2. k – 8 k + 16 = 25 3. k 2 – 10. k – 8 = 0 k = 10 +/-√(100 + 96)] / 6 k = 4 y k = – 2 / 3 Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 13

Ejercicios • • • • Estudiar la posición relativa de una recta (exterior, tangente o secante) con respecto a la esfera de ecuación: (x – 1)2+(y + 1)2+(z – 1)2 = 32 / 3 Ejercicio 2: Siendo la recta r: (x, y, z) = (-1, 1, -1) + k(1 , 1) La distancia del centro, C(1 , – 1 , 1) a la recta es: i j k d(C, r) = |AC x u| / |u| = 1+1 -1 -1 1+1 / √(12+ 12+12) = 1 1 1 =|-4 i +4 k| / √ 3 = √(16+0+16) / √ 3 = 4. √ 2 / √ 3 Radio esfera: r = √(32 / 3) = 4. √ 2 / √ 3 Recta tangente pues d(C, r) = r = 4. √ 2 / √ 3 Hallemos el punto de tangencia de recta y esfera: En la recta: x = – 1 + k , y = 1 + k , z = – 1 + k En la esfera: (– 1 + k – 1)2+(1 + k + 1)2+(– 1 + k – 1)2 = 32 / 3 Operando: 3. k 2 – 4. k + 12 = 32 / 3 9. k 2 – 12. k + 4 = 0 k = 2/3, doble. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 14