Outils danalyse la mthode des moindres carres 1

Outils d’analyse: la méthode des moindres carrées

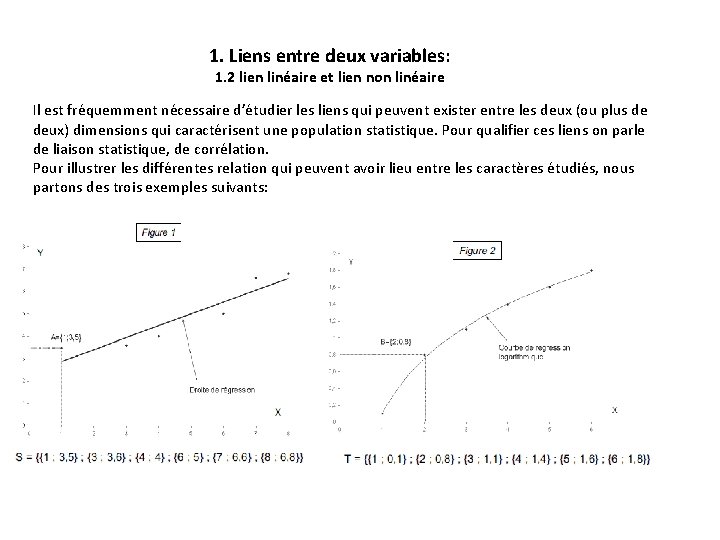
1. Liens entre deux variables: 1. 2 lien linéaire et lien non linéaire Il est fréquemment nécessaire d’étudier les liens qui peuvent exister entre les deux (ou plus de deux) dimensions qui caractérisent une population statistique. Pour qualifier ces liens on parle de liaison statistique, de corrélation. Pour illustrer les différentes relation qui peuvent avoir lieu entre les caractères étudiés, nous partons des trois exemples suivants:

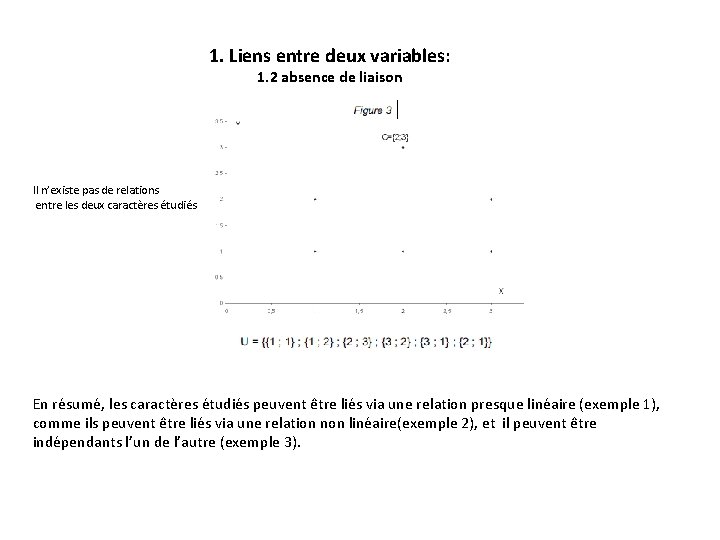
1. Liens entre deux variables: 1. 2 absence de liaison Il n’existe pas de relations entre les deux caractères étudiés En résumé, les caractères étudiés peuvent être liés via une relation presque linéaire (exemple 1), comme ils peuvent être liés via une relation non linéaire(exemple 2), et il peuvent être indépendants l’un de l’autre (exemple 3).

2. modèles de régressions non-linéaires Dans certaines situations expérimentales, la régression linéaire n'est pas appropriée: il faut donc recher d'autres modèles pour décrire la relation entre X et Y. Certains modèles peuvent se ramener à un modèle linéaire par une transformation mathématique des valeurs de X et/ou Y. On donne, dans cette partie, quelques modèles de régressions non-linéaires, et leurs transformations respectives pour obtenir une régression linéaire : Modèle exponentiel: Modèle puissance: Modèle double inverse:

2. 1. modèles de régressions exponentiel Modèle exponentiel: Le modèle exponentiel se linéarise en calculant le logarithme népérien de y. Exemple : Analyse de la croissance du nombre de campagnols par km 2 en fonction du temps. En pratique, étant donnée les yi, on calcul les y’i =ln(yi) pour obtenir de nouvelles données liées via une relation linéaire.

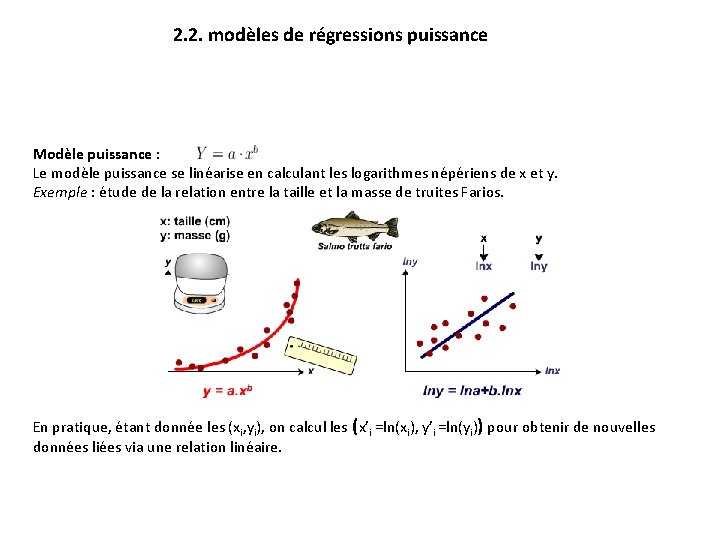
2. 2. modèles de régressions puissance Modèle puissance : Le modèle puissance se linéarise en calculant les logarithmes népériens de x et y. Exemple : étude de la relation entre la taille et la masse de truites Farios. En pratique, étant donnée les (xi, yi), on calcul les (x’i =ln(xi), y’i =ln(yi)) pour obtenir de nouvelles données liées via une relation linéaire.

2. 3. modèles de régressions double inverse Modèle double inverse : Le modèle double inverse et se linéarise en calculant les inverses de x et y : Exemple : analyse de la relation entre la concentration en substrat et la vitesse de réaction d'une enzyme. En pratique, étant donnée les (xi, yi), on calcul les (x’i =1/xi, y’i = 1/yi)) pour obtenir de nouvelles données liées via une relation linéaire.

3. La droite de régression linéaire

3. 1 définition de la droite de régression linéaire Définition: Le point moyen est le point qui a pour coordonnées la moyenne de X et la moyenne de Y. On l’appelle aussi le centre de gravité. Définition: La droite de régression est une droite qui passe par le point moyen. C'est aussi la droite qui minimise la somme des carrés des écarts des observations; voir la figure ci-dessous. Une fois connue, l'équation de cette droite permet de résumer la série et de faire des prévisions.

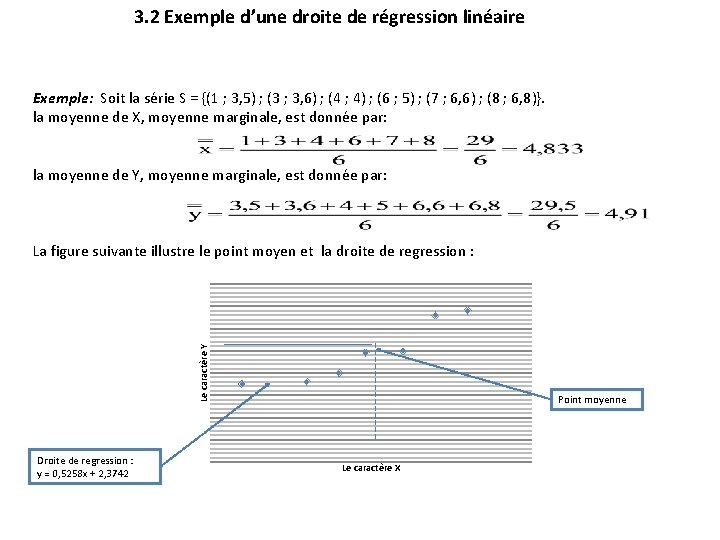
3. 2 Exemple d’une droite de régression linéaire Exemple: Soit la série S = {(1 ; 3, 5) ; (3 ; 3, 6) ; (4 ; 4) ; (6 ; 5) ; (7 ; 6, 6) ; (8 ; 6, 8)}. la moyenne de X, moyenne marginale, est donnée par: la moyenne de Y, moyenne marginale, est donnée par: Le caractère Y La figure suivante illustre le point moyen et la droite de regression : Droite de regression : y = 0, 5258 x + 2, 3742 Point moyenne Le caractère X

3. 3. coefficients de la droite de régression Soit la droite d’équation : y=ax+b Pour ajuster cette droite à un nuage de points dans le plan (X, Y), il faut calculer les coefficients a et b en appliquant les formules suivantes :

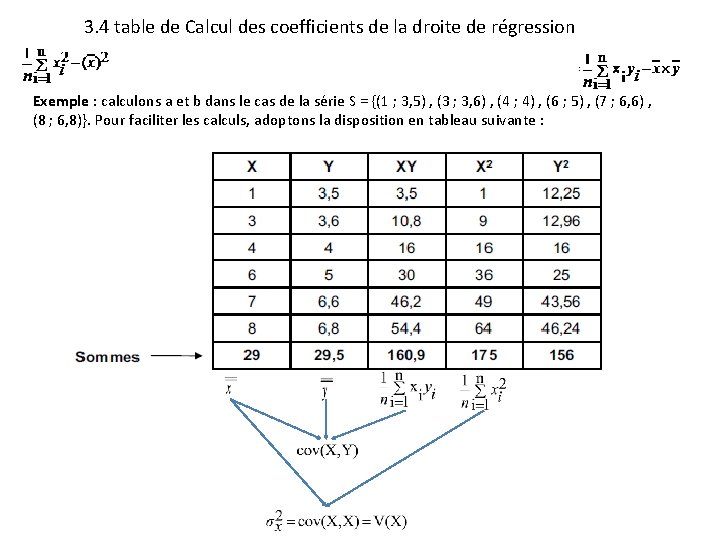
3. 4 table de Calcul des coefficients de la droite de régression Exemple : calculons a et b dans le cas de la série S = {(1 ; 3, 5) , (3 ; 3, 6) , (4 ; 4) , (6 ; 5) , (7 ; 6, 6) , (8 ; 6, 8)}. Pour faciliter les calculs, adoptons la disposition en tableau suivante :

3. 5 Calcul des coefficients de la droite de régression Exemple : calculons a et b dans le cas de la série S = {(1 ; 3, 5) , (3 ; 3, 6) , (4 ; 4) , (6 ; 5) , (7 ; 6, 6) , (8 ; 6, 8)}. Pour faciliter les calculs, adoptons la disposition en tableau suivante :

3. 6. utilités de la droite de régression

4. coefficient de corrélation Les deux caractères sont très liés

4. 5. coefficient de corrélation et droite de régression