New Results on Computing in Games Tuomas Sandholm

New Results on Computing in Games Tuomas Sandholm Carnegie Mellon University Computer Science Department Joint work with Vincent Conitzer

Interplay of computing & incentives • Computational complexity of – Executing a mechanism (rules of the game) • Determining the winners in – Voting [Bartholdi, Tovey, Trick 89] – Combinatorial auctions [Sandholm AIJ-02, …] – Executing a strategy • How should computationally bounded agents play strategically? { – Limits on memory [Rubinstein, Papadimitriou, Kalai, Gilboa, …] – Costly or limited computing [Sandholm ICMAS-96, IJEC-00; Larson&Sandholm AIJ-01, AAMAS-02, TARK-01, AGENTS-01 workshop, …] – Manipulating a mechanism (by determining a beneficial insincere revelation) – Determining which agents’ preferences should be elicited – Determining how to play (finding the game’s equilibrium) – Finding a payoff division (e. g. , according to the core) – Designing a mechanism

Complexity of Manipulating Elections with Few Candidates [Conitzer & S. , National Conference on Artificial Intelligence (AAAI), 2002]

Voting • Agents may have conflicting preferences • In aggregate, must choose one from a set of candidates – – Deciding on a president/leader/coordinator/representative Joint plans Allocations of tasks/resources … • Voting is most general preference aggregation method – Applicable to any preference aggregation setting – No side payments • Voting can be done without side payments • Side payments are not always technically possible or politically viable • Side payments from a finite set -> could be incorporated into candidates

Manipulation in voting • A voter is said to manipulate when it does not rank the candidates truthfully • Example (in plurality voting) – Voter A prefers Nader to Gore to Bush – But Nader is extremely unlikely to win – So, voter A votes for Gore • Why is manipulation bad? – Voting protocol is designed to maximize social welfare => Manipulation will cause a suboptimal outcome to be chosen – If protocol relies on manipulation to choose right outcome, there exists another nonmanipulable protocol that chooses same outcome (Revelation Principle)

Common voting protocols • Plurality (candidate with most votes wins) • Single Transferable Vote (STV) – Each round, candidate with fewest votes drops out – When your candidate drops out, your vote transfers to your next most preferred (remaining) candidate – Now A can safely vote for Nader, then let the vote transfer to Gore – Supporting a candidate may hurt that candidate! • Supporting a weaker opponent instead can cause a tougher opponent to be eliminated • Borda – Every voter ranks all candidates – 0 points for the bottom candidate, 1 for the second-to-last, … • Copeland – Every voter ranks all candidates – From this, pairwise elections between candidates are simulated – Candidate with most pairwise victories wins • Maximin – Candidate with best score in its worst pairwise election wins • Approval – Every voter either approves or disapproves each candidate – Candidate with most approvals wins

Manipulation of voting protocols • Seminal impossibility result [Gibbard-Satterthwaite]: all nondictatorial voting protocols with >2 candidates are manipulable • Software agents may manipulate more than humans in practice – – Humans might not consider the option of manipulation Many humans insufficiently understand (the manipulability of) protocols Manipulation algorithms may be too tedious to run by hand For software agents, voting algorithms must be coded explicitly • Rational strategic algorithms are preferred • The voting algorithm needs to be coded only once • Software agents are good at running algorithms • Idea: Use computational complexity as the barrier to manipulation

Prior research • Individually manipulating Second-order Copeland is NP-complete [Bartholdi, Tovey, Trick 1989] – Somewhat contrived result relying on tie-breaking • Individually manipulating STV is NP-complete [Bartholdi, Orlin 1991] • Those results rely on the number of candidates (m) being unbounded • We designed a recursive algorithm for individually manipulating STV with O(m^1. 62) calls (and usually much fewer) – Not too complex for realistic numbers of candidates

Manipulation complexity with few candidates • Ideally, would like complexity results for constant number of candidates • But then manipulator can simply evaluate each possible vote – assuming the others’ votes are known • Even for coalitions, only polynomially many effectively different votes • However, if we place weights on votes, complexity may return… Unbounded #candidates Constant #candidates Unweighted Weighted voters Individual manipulation Can be hard easy Coalitional manipulation Can be hard easy Potentially hard

Why study weighted coalitional manipulation? • In large elections, usually impossible to manipulate individually • Many real world elections have weights – E. g. electoral college – Weights more likely with heterogeneous software agents • Weighted coalitional manipulation is more realistic than assuming unbounded #candidates • We also derive other individual/unweighted results from results in this setting

Constructive manipulation • A coalition wants a certain candidate p to win • Thrm. NP-complete for Borda, STV, Copeland, Maximin – For 3, 3, 4, 4 candidates respectively • Proof sketch for Borda: – p is trailing the two other candidates, who are tied – Naturally, colluders give p their first vote – But must carefully divide their second votes across other candidates – This is basically doing PARTITION

Destructive manipulation • A coalition wants a certain candidate h to not win • Thrm. Easy for Borda, Copeland, Maximin, even with unbounded numbers of candidates – The algorithm relies on these methods being score-based and monotonic (more support always helps) • Thrm. NP-complete for STV (even with 4 candidates) – Proof reduces constructive STV to destructive STV • Sometimes, to get a candidate to not win, the coalition needs to get a specific other candidate to the final round

Randomization can be used to make manipulation hard • Consider the Cup protocol: – Candidates play an elimination tournament based on pairwise elections b c b a b c d • Given the schedule (leaf labels), any type of manipulation is easy even with unbounded #candidates – For each node in tree, can build the set of candidates that would reach this node for some vote by the coalition (from bottom up) • Manipulating a subtree only requires commitment on the order of candidates in that subtree • Idea: randomize (uniformly) over schedules after votes received • Theorem. Manipulating Randomized Cup is NP-complete – Proof is complex & uses 7 candidates

Uncertainty about others’ votes Even individual weighted manipulation can be hard • So far we assumed that manipulator(s) know the others’ votes – Unrealistic -> drop this assumption • Theorem. Whenever constructive coalitional manipulation is hard under certainty, individual manipulation is hard under uncertainty – Holds even when manipulator’s vote is worthless • i. e. we just wish to evaluate an election – Even with very limited kinds of uncertainty • Independence • All votes either completely known or not at all – Proof sketch. When manipulator’s vote is worthless, it is difficult to figure out if a certain candidate has a chance of winning, because this requires a constructive vote by the unknown voters

Uncertainty about others’ votes Even individual unweighted manipulation can be hard • Let’s drop the assumption of independence between voters – Usually votes are highly correlated – Identical software agents will vote identically • Theorem. Whenever evaluating an election is hard with independent weighted voters, it is hard with correlated unweighted voters – Even with very limited kinds of correlation • Perfect correlation or independence – Proof sketch. Just replace a vote of weight k by k unweighted, perfectly correlated voters • So, – because evaluation with independent weighted voters is hard for Borda, Copeland, Maximin and STV, – evaluation is hard for those protocols even for (correlated) unweighted voters

What do our results suggest? • All of the protocols we discussed are computationally more manipulation-proof than Plurality • Among these, STV seems inherently least manipulable • Randomizing the protocol can make manipulation hard • Manipulation is computationally difficult because usually there is uncertainty about others’ votes

Vote Elicitation: Complexity and Strategy-Proofness [Conitzer & S. , National Conference on Artificial Intelligence (AAAI), 2002]

Vote elicitation • Eliciting votes selectively can allow election to be terminated early – But the outcome of the election should be unchanged • Why minimize preference revelation? – Costly for agents to compute their preferences – Communicating preferences causes overhead • Traveling to the voting booth • Network traffic – Less revelation is desirable due to privacy reasons

Vote elicitation … • In deciding which votes to elicit, the most effective elicitation schemes make use of – Suspicions about how the agents will vote • Can come from – Votes in previous elections – Understanding the relationship between candidates & voters • In a 2 -candidate election, if the elicitor knows beforehand who will vote for the winner, it can simply elicit enough of these – Elicitation results so far

Impediments to effective elicitation • Computational complexity issues – How hard to know if elicitation can be terminated? – How hard to decide which votes to elicit? • Strategic issues – Does elicitation introduce (additional) opportunities for manipulating the election?

Hardness of terminating elicitation • How hard is it to know if we are done? • Theorem. For the STV protocol, it is NP-complete! – NP-complete even if only one voter remains to be elicited – When voters are weighted, NP-complete even with only 4 candidates – Proof idea. Reductions are from problems on manipulating elections • Intuition: we can terminate if and only if the remaining candidates cannot “conspire” to make the leader lose • Theorem. In all score-based, monotone protocols, terminating elicitation is easy (even with weighted voters) – A protocol is monotone if more support never hurts a candidate – Plurality, Borda, Copeland, Maximin, Approval satisfy these conditions – Proof sketch. For each nonleading candidate, check if it would win if all remaining voters supported it most, and the leader least

Hardness of deciding whom to elicit • Theorem. PSPACE-hard (for Approval) – Proof. Long reduction from STOCHASTIC-SAT • Theorem. NP-complete even with perfect suspicions about how voters will vote – Holds for all of the protocols except Plurality • For Plurality, elicit voters voting for the winner first • Then, going through the remaining candidates in a round-robin manner, elicit a vote for that candidate (if possible) – Proofs. Reductions from EXACT-COVER-BY-3 -SETS • If each losing candidate needs exactly one more “bad” vote to be eliminated, and each vote is “bad” for exactly 3 candidates, we should try to “cover” the candidates exactly with these 3 -sets • Or, a vote may be “good” for 3 losing candidates, and it may be necessary to avoid eliciting more than one more “good” vote per losing candidate to terminate quickly

Hardness of deciding whom to elicit: Varying weights & elicitation costs • Voters may be weighted • Also, cost of eliciting a voter may vary across voters • Theorem. With both of these, effective elicitation is NP -complete for all protocols, even with only 2 candidates – even if voter’s elicitation cost can only be 0 or equal to weight – All voting protocols coincide with 2 candidates • Theorem. If only weights or costs vary across voters, deciding whom to elicit is easy – for any constant number of candidates

Coarse & fine elicitation • Two types of vote elicitation – Coarse elicitation: Whoever is elicited, reveals her complete vote – Fine elicitation: Some voters reveal their votes partially • E. g. , no need to rank candidate x because it has already lost • Coarse elicitation reduces the traveling costs to the voting booth & effort of determining one’s preferences • Fine elicitation further reduces effort of determining one’s preferences

Strategic issues in coarse elicitation • Theorem. Even if the following all hold – – Voters are unweighted & elicitation costs are uniform Truthful voting is a Bayes-Nash equilibrium without elicitation Our (coarse) elicitation policy is optimized to finish ASAP on average An agent learns nothing about the other agents votes when elicited, except how many other agents were elicited before it • An agent could infer this from the time at which it is elicited • then it is possible that with elicitation – Truthful voting is no longer a Bayes-Nash equilibrium – Agents condition how they vote on when they are elicited • Theorem. If we can prevent an agent from learning how many other agents have been elicited so far, the set of Bayes-Nash equilibria does not change with elicitation

Strategic issues in fine elicitation • Theorem. Even if the following all hold – Voters are unweighted & elicitation costs are uniform – Truthful voting is a Bayes-Nash equilibrium without elicitation – Our (fine) elicitation policy is optimized to finish ASAP on average • then it is possible that with elicitation – Truthful voting is no longer a Bayes-Nash equilibrium – Agents condition how they vote on the order of queries to them • I. e. , fine elicitation introduces strategic issues even when nothing is learned about how many agents were elicited before – Voter can condition on the order of queries to it • Theorem. If – order of queries to an agent depends only on answers that it gave to previous queries (but not other agents’ answers), and – nothing can be inferred about how many agents were elicited so far • then the set of Bayes-Nash equilibria does not change with elicitation

Complexity Results about Nash Equilibria [Conitzer & S. , CMU Computer Science Department technical report, 2002]

Complexity of equilibrium concepts from noncooperative game theory • Solutions are less useful if they cannot be determined – So, their computational complexity is important • Early research studied complexity of board games – E. g. chess, Go – Complexity results here usually depend on structure of game (allowing for concise representation) – Usually zero-sum, alternating move • Real-world strategic settings are much richer – Concise representation for all games is impossible – Not necessarily zero-sum/alternating move – Sophisticated agents need to be able to deal with such games…

Complexity of Nash equilibria • Game theory defines – General representations of games – Solution concepts for these games • Most central is Nash equilibrium • Any finite game has a mixed-strategy Nash equilibrium [Nash 1950] • Complexity of finding a mixed-strategy Nash equilibrium? – Still an open question! – “Together with factoring … the most important concrete open question on the boundary of P today” [Papadimitriou 2001] • We solved several related questions…

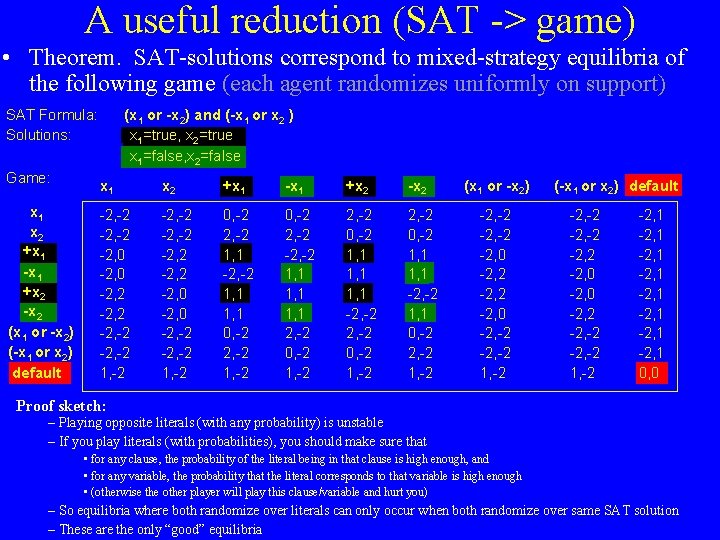
A useful reduction (SAT -> game) • Theorem. SAT-solutions correspond to mixed-strategy equilibria of the following game (each agent randomizes uniformly on support) SAT Formula: Solutions: Game: x 1 x 2 +x 1 -x 1 +x 2 -x 2 (x 1 or -x 2) (-x 1 or x 2) default (x 1 or -x 2) and (-x 1 or x 2 ) x 1=true, x 2=true x 1=false, x 2=false x 1 x 2 +x 1 -x 1 +x 2 -2, -2 -2, 0 -2, 2 -2, -2 1, -2 -2, 2 -2, 0 -2, -2 1, -2 0, -2 2, -2 1, 1 -2, -2 1, 1 0, -2 2, -2 1, -2 0, -2 2, -2 -2, -2 1, 1 2, -2 0, -2 1, -2 2, -2 0, -2 1, 1 -2, -2 0, -2 1, -2 2, -2 0, -2 1, 1 -2, -2 1, 1 0, -2 2, -2 1, -2 (x 1 or -x 2) -2, -2 -2, 0 -2, -2 1, -2 (-x 1 or x 2) default -2, -2 -2, 0 -2, 2 -2, -2 1, -2 -2, 1 -2, 1 0, 0 Proof sketch: – Playing opposite literals (with any probability) is unstable – If you play literals (with probabilities), you should make sure that • for any clause, the probability of the literal being in that clause is high enough, and • for any variable, the probability that the literal corresponds to that variable is high enough • (otherwise the other player will play this clause/variable and hurt you) – So equilibria where both randomize over literals can only occur when both randomize over same SAT solution – These are the only “good” equilibria

Complexity of mixed-strategy Nash equilibria with certain properties • This reduction implies that there is an equilibrium where players get expected utility 1 each iff the SAT formula is satisfiable – Any reasonable objective would prefer such equilibria to 0 -payoff equilibrium • Corollary. Deciding whether a “good” equilibrium exists is NP-hard: – – 1. equilibrium with high social welfare 2. Pareto-optimal equilibrium 3. equilibrium with high utility for a given player i 4. equilibrium with high minimal utility • Also NP-hard (from the same reduction): – 5. Does more than one equilibrium exists? – 6. Is a given strategy ever played in any equilibrium? – 7. Is there an equilibrium where a given strategy is never played? • (5) & weaker versions of (4), (6), (7) were known [Gilboa, Zemel GEB-89] • All these hold even for symmetric, 2 -player games

Counting the number of mixed-strategy Nash equilibria • Why count equilibria? If we cannot even count the equilibria, there is little hope of getting a good overview of the overall strategic structure of the game • Unfortunately, our reduction implies: – Corollary. Counting Nash equilibria is #P-hard! • Proof. #SAT is #P-hard, and the number of equilibria is 1 + #SAT – Corollary. Counting connected sets of equilibria is just as hard • Proof. In our game, each equilibrium is alone in its connected set – These results hold even for symmetric, 2 -player games

Complexity of Bayes-Nash equilibria • Players have private information about their preferences (types) • Finding pure-strategy equilibria – Easy for normal form games (simply check all combinations of strategies) – Now strategy may depend on type -> too many combinations to check • Pure strategy equilibria are desirable – Avoids randomization over strategies between which players are indifferent • Theorem. Deciding whether a pure-strategy Bayes-Nash equilibrium exists is NP-complete – Proof sketch. (easy to make symmetric) • Each of player 1’s strategies, even if played with low probability, makes some of player 2’s strategies unappealing to player 2 • With these, player 1 wants to “cover” all of player 2’s strategies that are bad for player 1. But player 1 can only play so many strategies (one for each type) • This is SET-COVER

Complexity of Nash equilibria in stochastic (Markov) games • • We now shift attention to games with multiple stages Some NP-hardness results have already been shown here Ours is the first PSPACE-hardness result (to our knowledge) We focus on Markov games – At each stage, the game is in a certain state – State transition probabilities depend on current state & players’ current actions – State affects the payoffs that players receive • PSPACE-hardness results from e. g. Go do not carry over – Go has an exponential number of states – For general representation, we need to specify states explicitly

Complexity of Nash equilibria in stochastic (Markov) games… • Strategy spaces here are rich (agents can condition on past events) – So maybe high-complexity results are not surprising … • High-complexity even when players cannot condition on anything! – No feedback from the game: the players are playing “blindly” • Theorem. Even under this restriction, deciding whether a purestrategy Nash equilibrium exists is PSPACE-hard – even if game is 2 -player, symmetric, and transition process is deterministic – Proof sketch. Reduction is from PERIODIC-SAT, where an infinitely repeating formula must be satisfied [Orlin, 81] • Theorem. NP-hard even if game has a finite number of stages

Complexity of Determining Nonemptiness of the Core [Conitzer & S. , CMU Computer Science Department technical report, 2002]

Complexity of Mechanism Design [Conitzer & S. , UAI-02 & new draft]

Automated mechanism design • Mechanism design = designing rules of game so that a good outcome happens although agents play strategically • Idea: Solve mechanism design as an optimization problem automatically – Inputs: outcomes, type space, prior, designer’s objective – Output: optimal mechanism – Creating a mechanism for the specific setting (instance) at hand General preferences rather than a class of settings – Advantages: Quasilinear prefs • Can circumvent impossibility results • Can be used even in settings that do not satisfy the assumptions of canonical mechanisms (e. g. quasilinear utility functions) • Can lead to a greater value of the mechanism designer’s objective (or stronger notions of nonmanipulability) than canonical mechanisms • Often designer has info about agents - silly to ignore

Defining the computational problem: Input • An instance is given by – Set of possible outcomes – Set of agents • For each agent – set of possible types – probability distribution over these types – utility function converting type/outcome pairs to utilities – Objective function • Gives a value for each outcome for each combination of agents’ types • E. g. social welfare – Restrictions on the mechanism • Are side payments allowed? • Is randomization over outcomes allowed? • What concept of nonmanipulability is used?

Defining the computational problem: Output • The algorithm should produce – a mechanism • A mechanism maps combinations of agents’ revealed types to outcomes – Randomized mechanism maps to probability distributions over outcomes – Also specifies payments by agents (if side payments are allowed) – … which • is nonmanipulable (according to the given concept) – By revelation principle, we can focus on truth-revealing direct-revelation mechanisms w. l. o. g. • maximizes the expectation of the objective function

Our results on the complexity of mechanism design • Social welfare objective: Deterministic mechanism no payments NP-complete payments Polynomial time (MINSAT) Randomized mechanism Polynomial time (Groves) Polynomial time (LP) • General objective functions: Deterministic mechanism no payments NP-complete (MINSAT) Randomized mechanism Polynomial time (INDEPENDENT-SET) (LP) Polynomial time These results hold even for just 2 agents

Thank you for your attention ! Papers on these topics are available at www. cs. cmu. edu/~sandholm