Mtodo de Euler O mtodo de Euler para



![Podemos, porém, melhorar esta aproximação se subdividirmos o intervalo [x 0 ; z ] Podemos, porém, melhorar esta aproximação se subdividirmos o intervalo [x 0 ; z ]](https://slidetodoc.com/presentation_image_h2/b45c8bc927caac87dda0cffa6b0b1872/image-4.jpg)








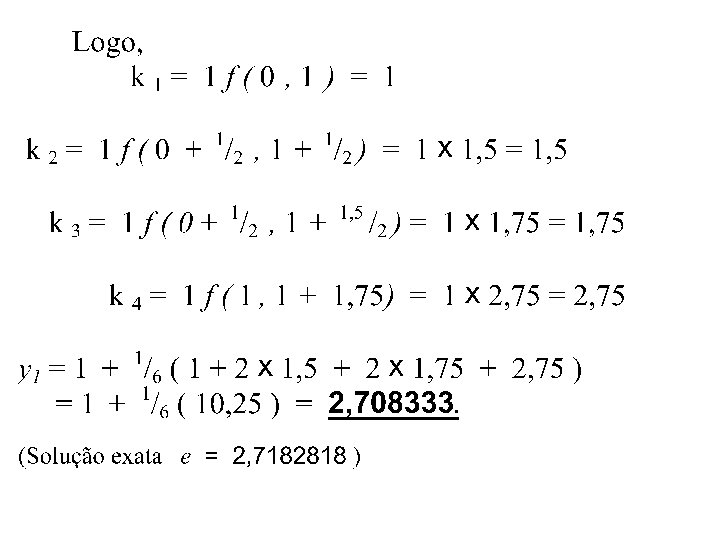




- Slides: 18

Método de Euler O método de Euler para resolver EDO com condições iniciais é o método numérico mais simples. Ele consiste em aproximar a solução y ( x ), no sentido de uma linearização, por meio de suas tangentes, Figura 1. Considere o problema ou seja, são dados um ponto de partida, (x 0 , y 0), e uma direção a ser tomada, f ( x, y ). Desejamos determinar y ( z ).

Métodos numéricos para resolver uma EDO Neste texto serão estudados métodos de passos simples e passos múltiplos para resolver equação de primeira ordem. Nos de passos simples necessitamos apenas dos resultados de yk , do passo anterior, para determinarmos a aproximação de yk+1. Enquanto que nos de passos múltiplos para determinarmos a aproximação y k+1 dependemos dos valores de y k, y k - 1. .

A interpretação geométrica da Figura 1 nos permite escrever a equação: y y 1 y(x) y 0 F ’(x 0 ) = y’ (x 0) = f (x 0 , y 0) x h x 0 z = x 1 Interpretação geométrica do Método de Euler Fazendo x 1 – x 0 = h, vamos ter y 1 = y 0 + h f (x 0 , y 0) ou F(x 1) F(x 0) + F ’(x 0) (x 1 – x 0 ) (Taylor). Diremos, portanto, que y 1 F(x 1) = F( z ) Em verdade, estamos substituindo a função desconhecida y ( x ) por, simplesmente uma reta em todo intervalo [x 0 ; z ] e calculando a imagem de z sobre ela o que pode ser uma aproximação ruim para y ( z ). Figura 1
![Podemos porém melhorar esta aproximação se subdividirmos o intervalo x 0 z Podemos, porém, melhorar esta aproximação se subdividirmos o intervalo [x 0 ; z ]](https://slidetodoc.com/presentation_image_h2/b45c8bc927caac87dda0cffa6b0b1872/image-4.jpg)
Podemos, porém, melhorar esta aproximação se subdividirmos o intervalo [x 0 ; z ] em subintervalos de amplitude constante, genericamente chamada h, e como sabemos calcular a direção da função incógnita y ( x ) em cada ponto, substituiremos tal y y(x) y 2 y 1 y 0 h x 0 x h x 1 z = x 2 Método de Euler considerando dois subintervalos Figura 2 função por um segmento de reta, em cada um destes subintervalos. Estes segmentos terão a direção que ela (função) tem no início de cada dos subintervalos, Figura 2. Obtemos então: y i + 1 = yi + h f (x i , y i ), i = 0, 1, . . . que vem a ser o método de Euler.








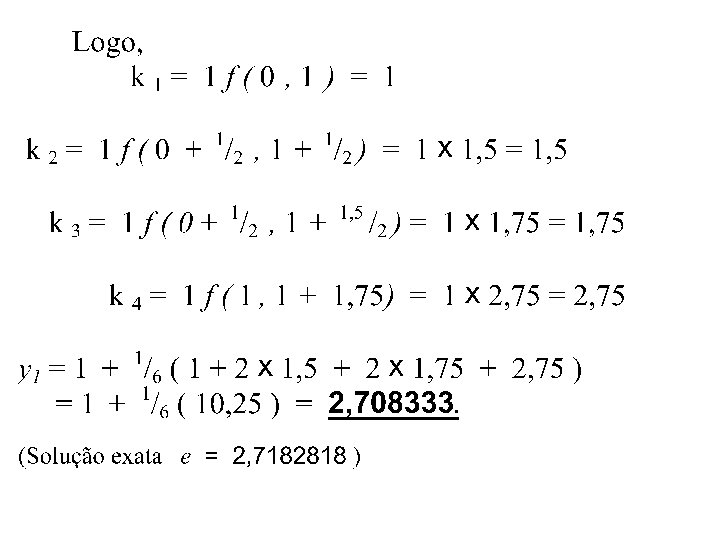


Métodos de passos Múltiplos Um método de passos simples determina a aproximação yk+1 em xk+1 = xk + h usando apenas o ponto de aproximação (xk , yk). Diferentemente deste, um método de passo múltiplo usa as informações de valores anteriores xk-1, xk-2, . . . , xk-m que são assumidos ser equidistantes para computar yk+1. O Método de Adams-Bashforth / Adams-Moulton é um método preditor - corretor como a fórmula modificada de Euler. A fórmula de Adams-Bashforth é dada por

yn+1 = yn + h / 24 (55 yn’ - 59 yn -1’ + 37 yn -2’ - 9 yn -3’), onde yn’ = f(xn , yn) Note que para calcular y 4 yn -1’ = f(xn -1 , yn -1) precisamos conhecer y 0 , y 1, yn -2’ = f(xn -2 , yn -2) y 2 e y 3. O valor de y 0 é a yn-3’ = f(xn -3 , yn -3) condição inicial e os valores y 1, y 2 e y 3 são calculados por um método como a fórmula de Runge-Kutta. Para n 3, como preditor, podemos levar o valor de yn+1 no corretor de Adams - Moulton e assim, obtermos

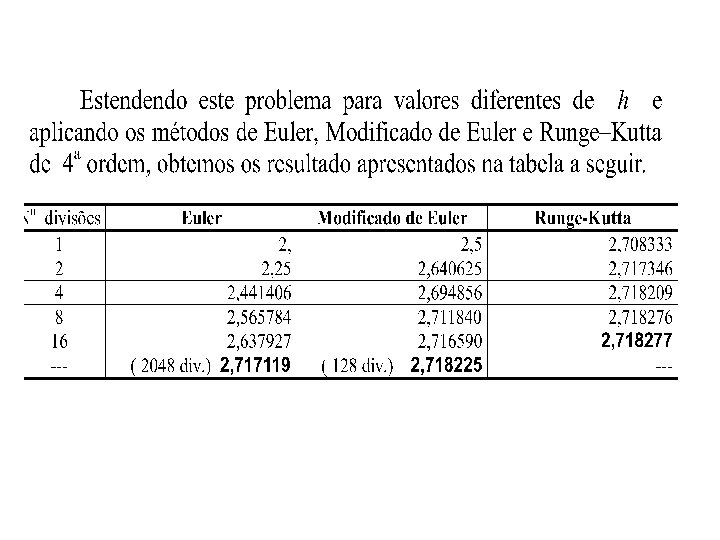
yn+1 = yn + h / 24 (9 yn +1’ + 19 yn ’ - 5 yn -1’ + yn -2’), com yn+1’ = f (xn+1, yn+1*) Exemplo: Aplique o método de Adams-Bashforth / Adams. Moulton com h = 0, 2 para obter uma aproximação de y(0, 8) para a solução de y’ = x + y -1, y(0) = 1. Solução: Com um passo h = 0, 2, y(0, 8) será aproximado por y 4. Inicialmente, aplicando o método de Runge-Kutta com x 0 = 0, . y 0 = 1 e h = 0, 2 para obtermos: y 1 = 1, 0214; y 2 = 1, 0918 e y 3 = 1, 2221.

Como f (x, y) = x + y -1, temos y 0’ = f (x 0, y 0) = f (0, 1) = ) + 1 - 1 = 0 y 1’ = f (x 1, y 1) = 0, 2 + 1, 0214 - 1 = 0, 2214 y 2’ = f (x 2, y 2) = 0, 4 + 1, 0918 - 1 = 0, 4918 y 3’ = f (x 3, y 3) = 0, 6 + 1, 2221 - 1 = 0, 8221 E assim, aplicando a fórmula de Adams-Bashforth, obtemos: y 4 = y 3 + 0, 2 / 24 (55 y 3’ - 59 y 2 ’ + 37 y 1’ - 9 y 0’) = 1, 4254. E para y 4’ = f (x 4, y 4*) = 0, 8 + 1, 4254 -1 = 1, 2254 Finalmente, y 4 = y 3 + 0, 2 / 24 (9 y 4’ +19 y 3 ’ - 5 y 2’ + y 1’) = 1, 4255. (Valor exato é 1, 4255)