15 2 Euler Paths and Euler Circuits 2010

§ 15. 2, Euler Paths and Euler Circuits © 2010 Pearson Prentice Hall. All rights reserved. 1

Objectives 1. 2. 3. 4. 5. Understand the definition of an Euler path. Understand the definition of an Euler circuit. Use Euler’s Theorem. Solve problems using Euler’s Theorem. Use Fleury’s Algorithm to find possible Euler paths and Euler circuits. © 2010 Pearson Prentice Hall. All rights reserved. 2

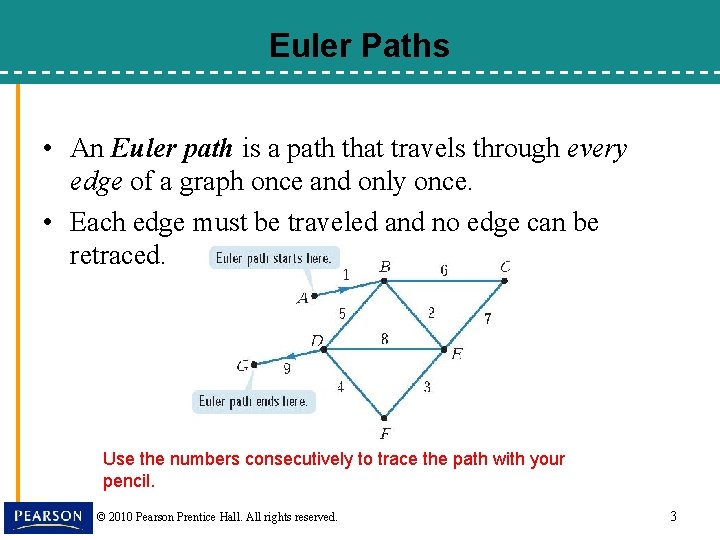
Euler Paths • An Euler path is a path that travels through every edge of a graph once and only once. • Each edge must be traveled and no edge can be retraced. Use the numbers consecutively to trace the path with your pencil. © 2010 Pearson Prentice Hall. All rights reserved. 3

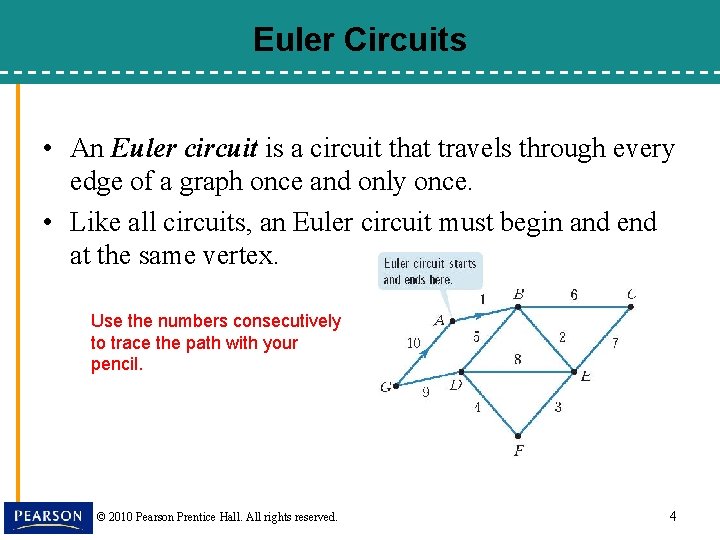
Euler Circuits • An Euler circuit is a circuit that travels through every edge of a graph once and only once. • Like all circuits, an Euler circuit must begin and end at the same vertex. Use the numbers consecutively to trace the path with your pencil. © 2010 Pearson Prentice Hall. All rights reserved. 4

Euler’s Theorem The following statements are true for connected graphs: 1. If a graph has exactly two odd vertices, then it has at least one Euler path, but no Euler circuit. Each Euler path must start at one of the odd vertices and end at the other one. 2. If a graph has no odd vertices (all even vertices), it has at least one Euler circuit (which, by definition, is also an Euler path). An Euler circuit can start and end at any vertex. 3. If a graph has more than two odd vertices, then it has no Euler paths and no Euler circuits. © 2010 Pearson Prentice Hall. All rights reserved. 5

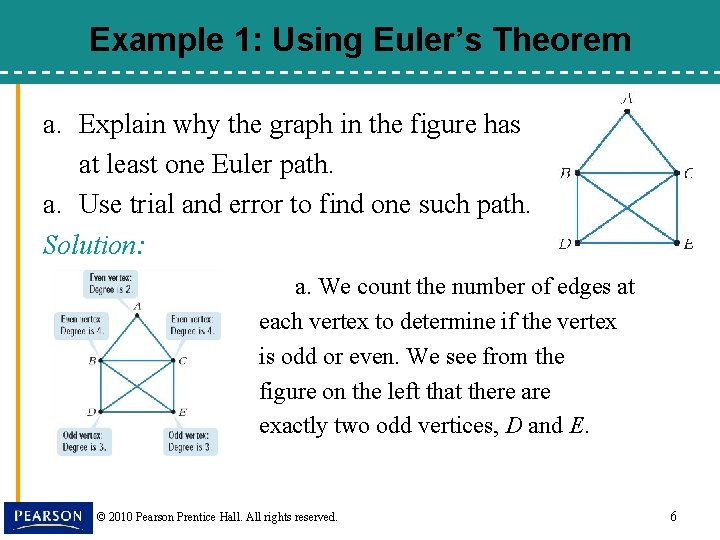
Example 1: Using Euler’s Theorem a. Explain why the graph in the figure has at least one Euler path. a. Use trial and error to find one such path. Solution: a. We count the number of edges at each vertex to determine if the vertex is odd or even. We see from the figure on the left that there are exactly two odd vertices, D and E. © 2010 Pearson Prentice Hall. All rights reserved. 6

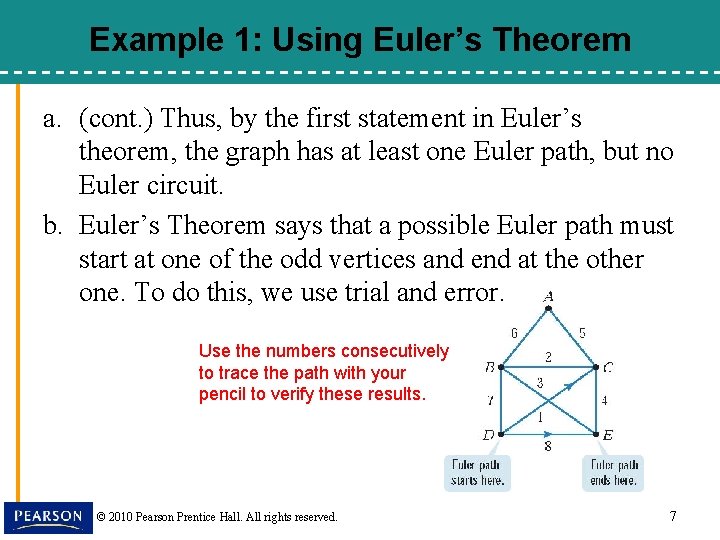
Example 1: Using Euler’s Theorem a. (cont. ) Thus, by the first statement in Euler’s theorem, the graph has at least one Euler path, but no Euler circuit. b. Euler’s Theorem says that a possible Euler path must start at one of the odd vertices and end at the other one. To do this, we use trial and error. Use the numbers consecutively to trace the path with your pencil to verify these results. © 2010 Pearson Prentice Hall. All rights reserved. 7

Applications of Euler’s Theorem Solving Problems Using Euler’s Theorem We can use Euler’s Theorem to solve problems involving situations modeled by graphs. Example: Recall the graph that models the layout of Königsberg. Count the number of odd vertices; there are four odd vertices. Because the graph has more than two odd vertices, it has no Euler paths. Thus, there is no possible way anyone in Königsberg can walk across all of the bridges without having to recross some of them. © 2010 Pearson Prentice Hall. All rights reserved. 8

Fluery’s Algorithm Finding Possible Euler Paths and Euler Circuits If Euler’s Theorem indicates the existence of an Euler path or Euler circuit, one can be found using this procedure: 1. If the graph has exactly two odd vertices, choose one of the two odd vertices as the starting point. If the graph has no odd vertices, choose any vertex as the starting point. 2. Number the edges as you trace through the graph according to the following rules: After you have traveled over an edge, erase it. Show the erased edge as a dashed line. When faced with a choice of edges to trace, first choose any edge that is not a bridge. [A bridge is an edge whose removal would make the graph disconnected. ] Travel over a bridge only if there is no alternative. © 2010 Pearson Prentice Hall. All rights reserved. 9

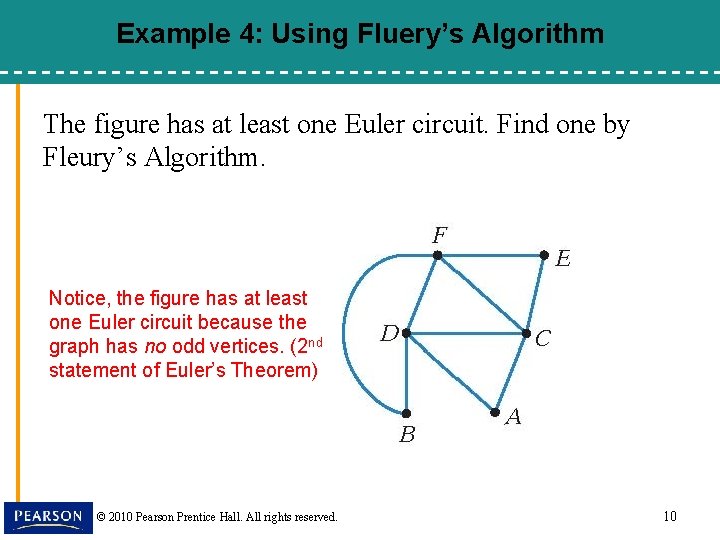
Example 4: Using Fluery’s Algorithm The figure has at least one Euler circuit. Find one by Fleury’s Algorithm. Notice, the figure has at least one Euler circuit because the graph has no odd vertices. (2 nd statement of Euler’s Theorem) © 2010 Pearson Prentice Hall. All rights reserved. 10

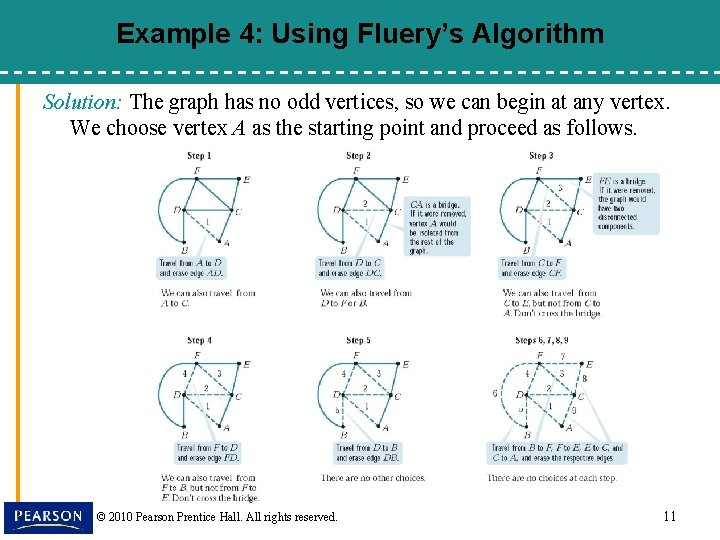
Example 4: Using Fluery’s Algorithm Solution: The graph has no odd vertices, so we can begin at any vertex. We choose vertex A as the starting point and proceed as follows. © 2010 Pearson Prentice Hall. All rights reserved. 11

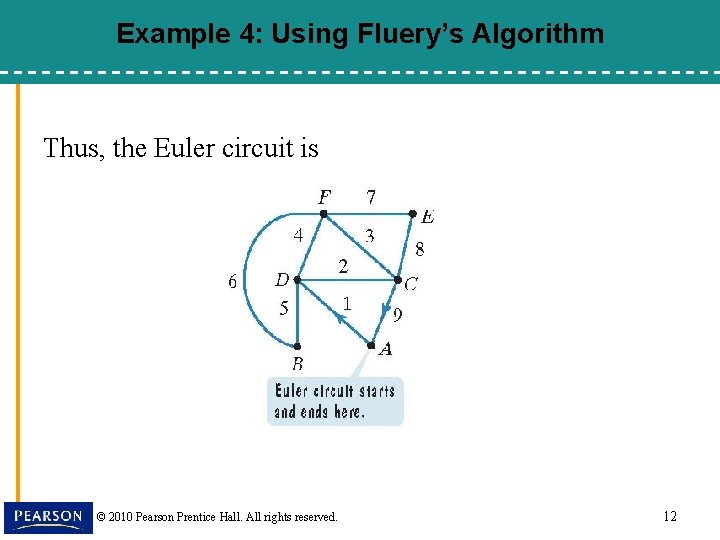
Example 4: Using Fluery’s Algorithm Thus, the Euler circuit is © 2010 Pearson Prentice Hall. All rights reserved. 12

• Page 838 – 839, #19 – 40. © 2010 Pearson Prentice Hall. All rights reserved.