ZYX Euler Angles ZYX Euler Angles Just three

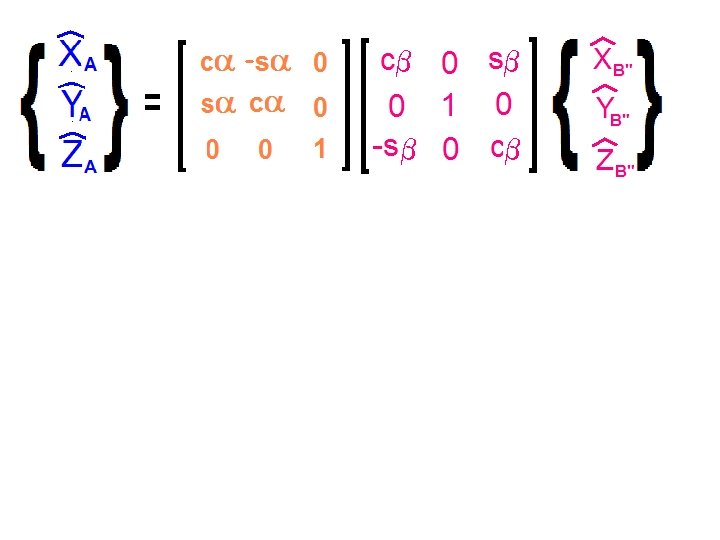
Z-Y-X Euler Angles

Z-Y-X Euler Angles - Just three numbers are needed to specify the orientation of one set of axes relative to another.

Z-Y-X Euler Angles -Just three numbers are needed to specify the orientation of one set of axes relative to another. -One possible set of these numbers is the Z -Y-X Euler angles

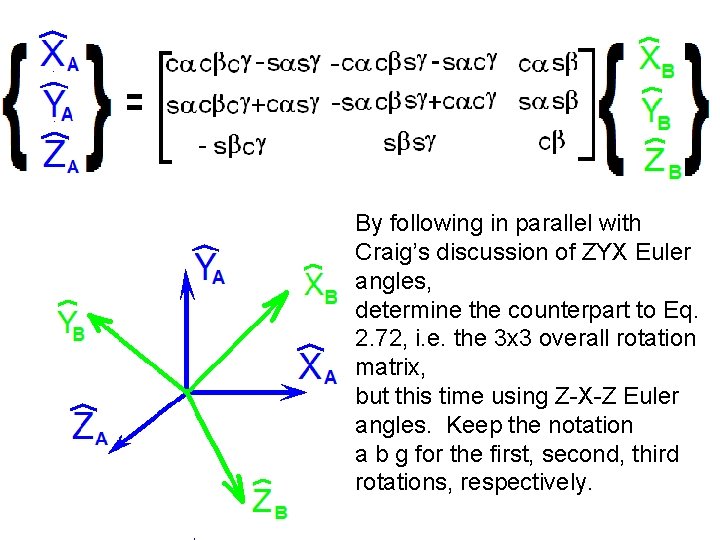
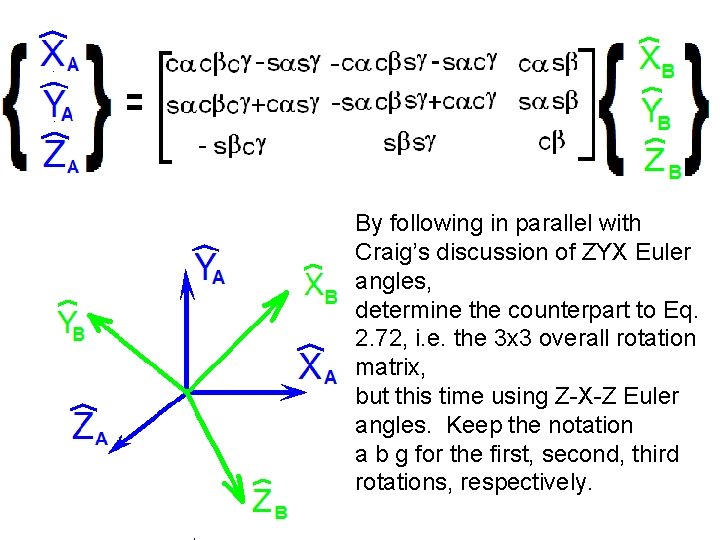
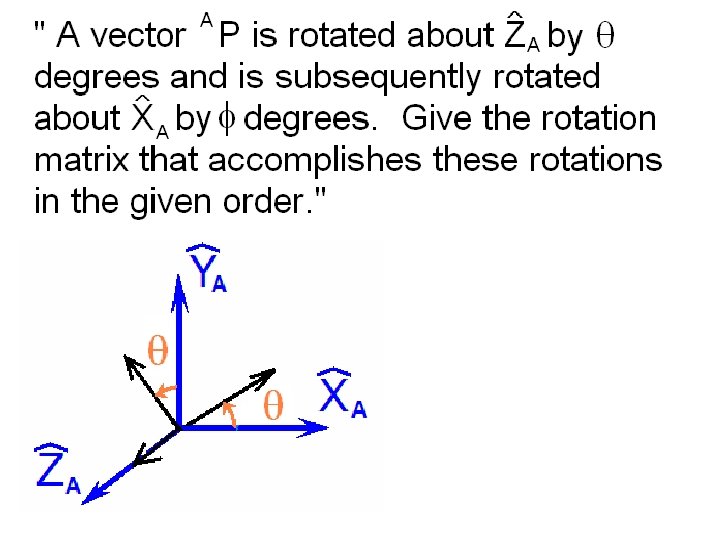
By following in parallel with Craig’s discussion of ZYX Euler angles, determine the counterpart to Eq. 2. 72, i. e. the 3 x 3 overall rotation matrix, but this time using Z-X-Z Euler angles. Keep the notation a b g for the first, second, third rotations, respectively.

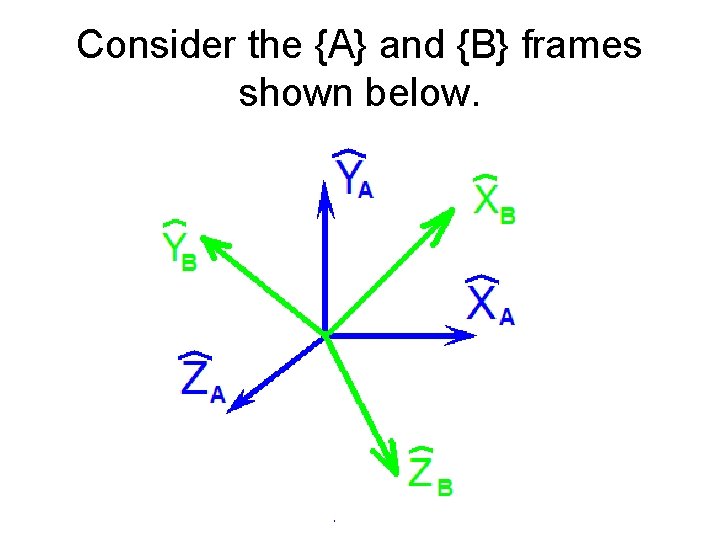
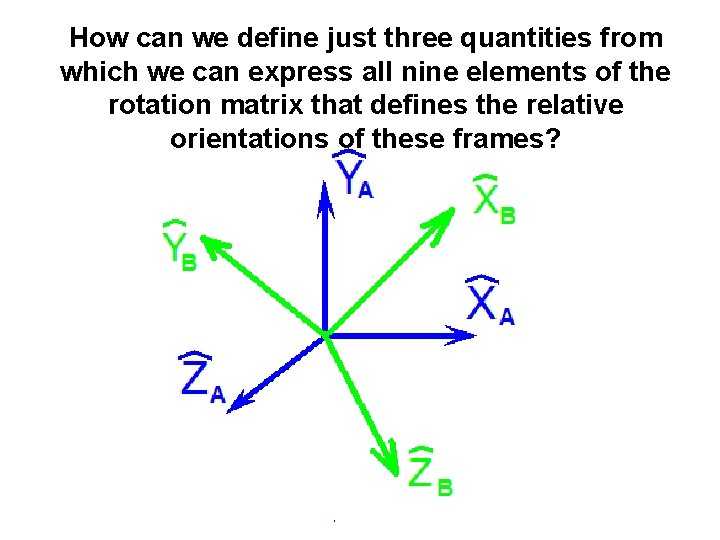
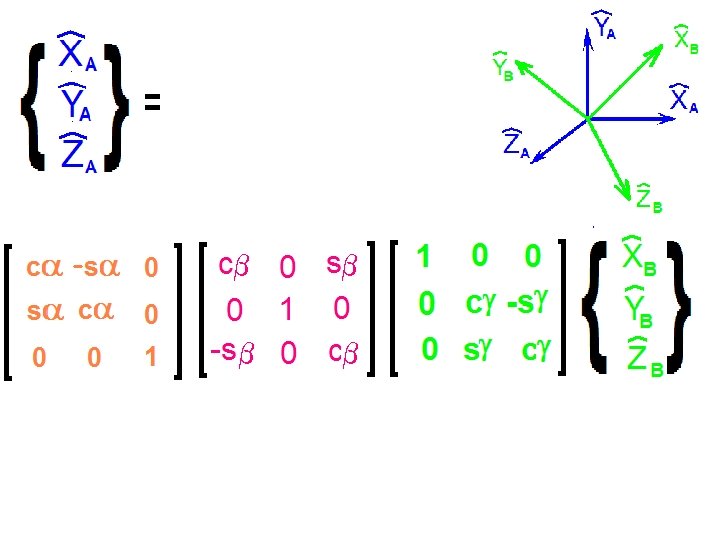
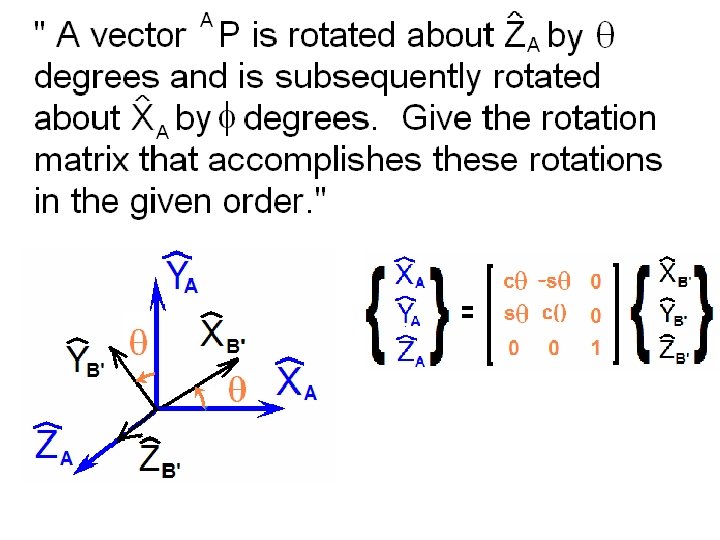
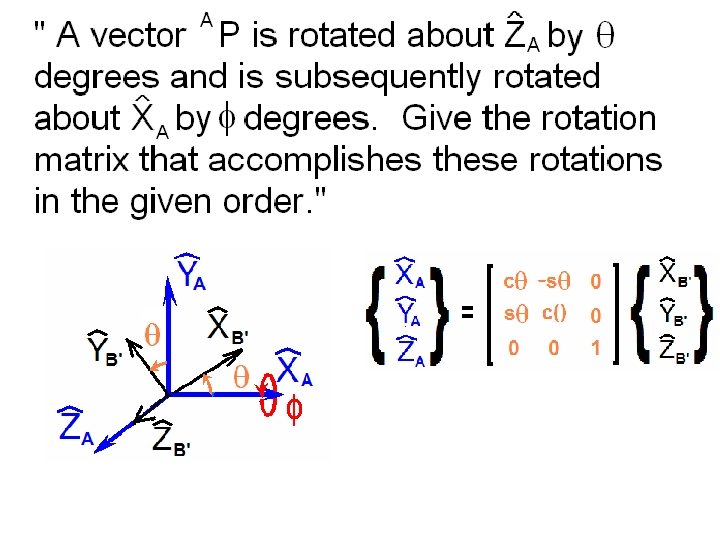
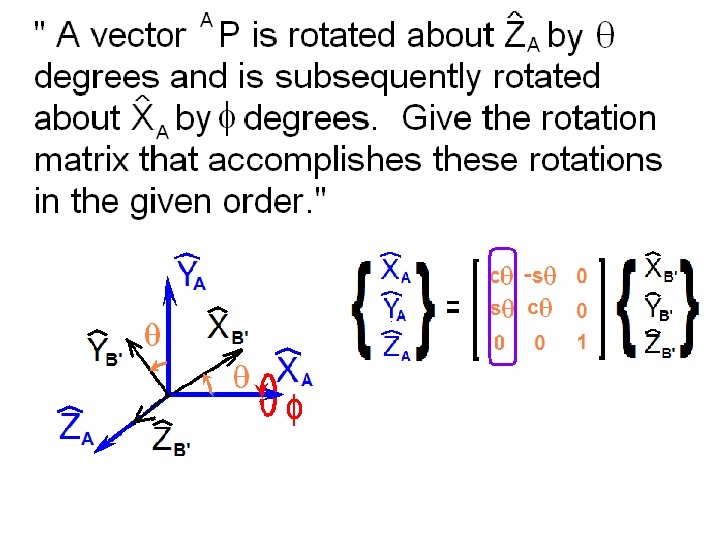
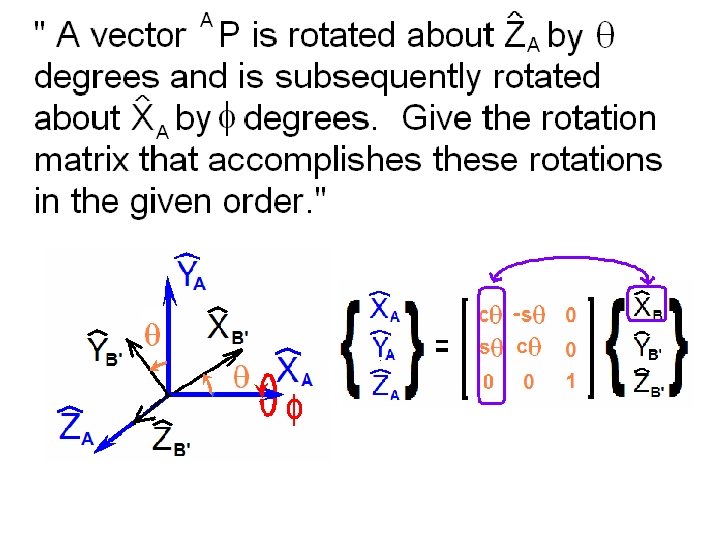
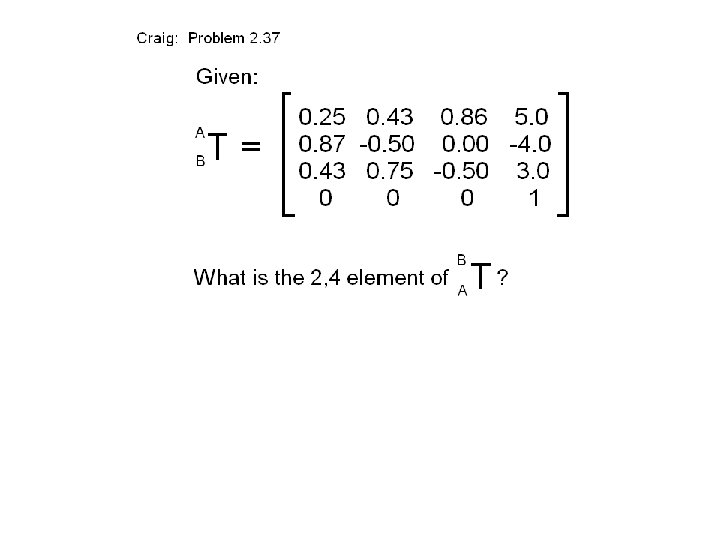
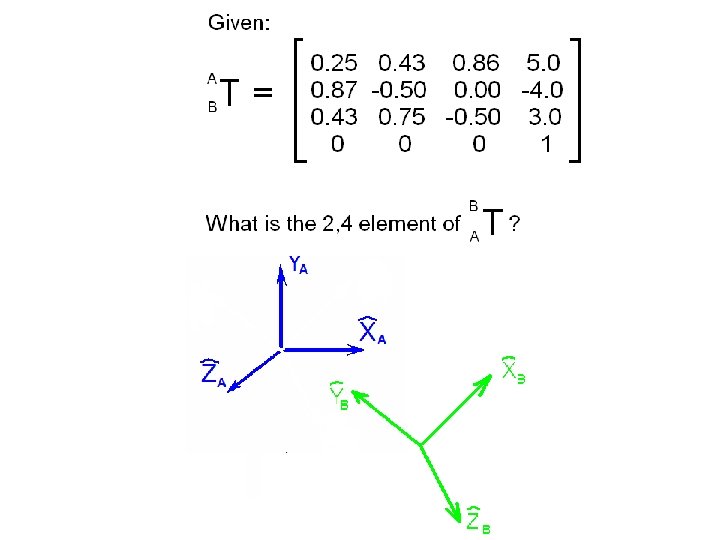
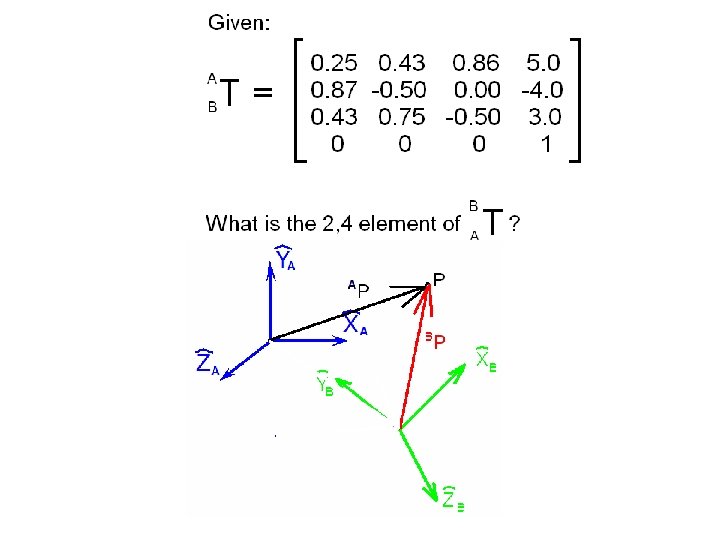
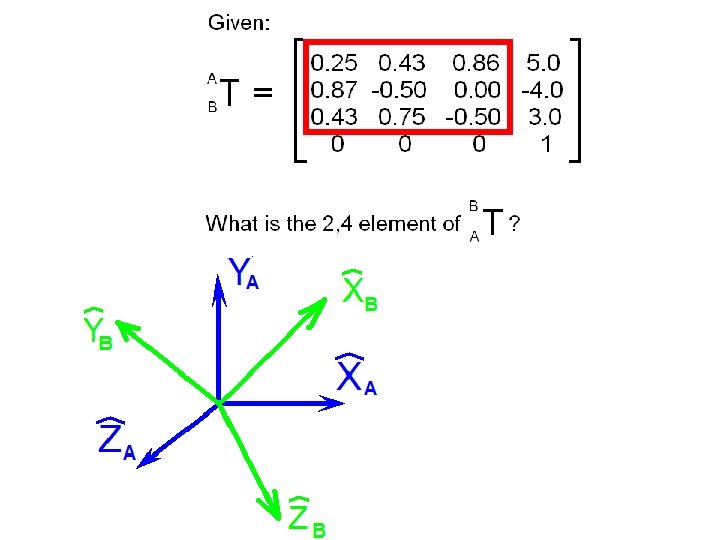
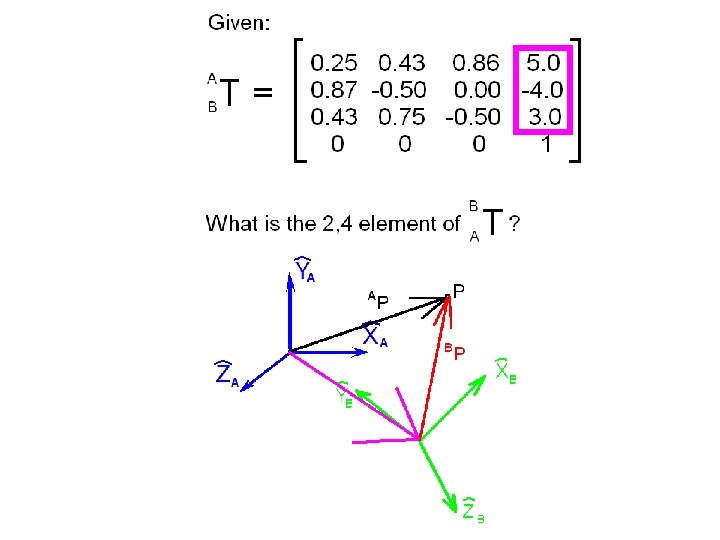
Consider the {A} and {B} frames shown below.

How can we define just three quantities from which we can express all nine elements of the rotation matrix that defines the relative orientations of these frames?

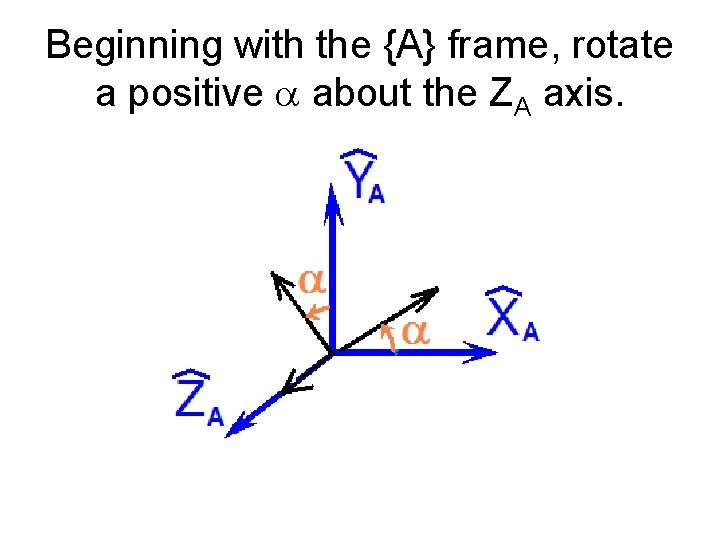
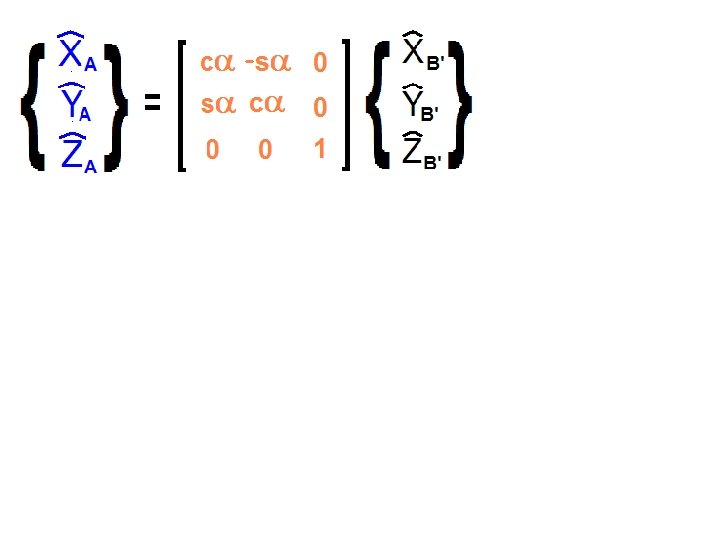
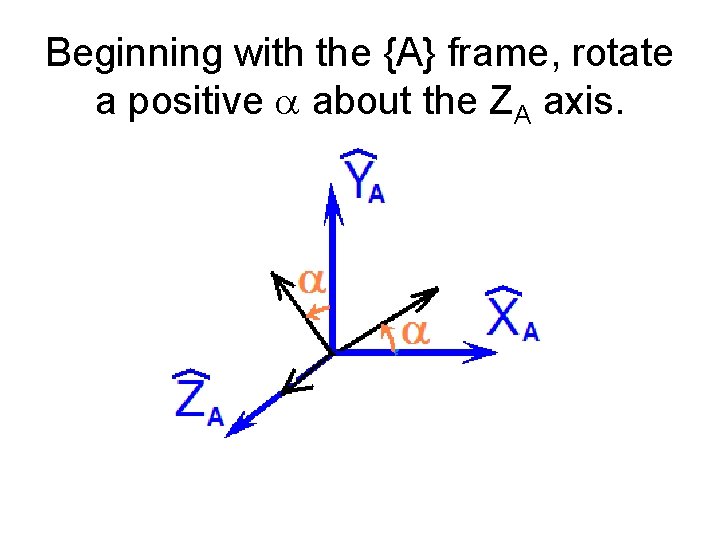
Beginning with the {A} frame, rotate a positive a about the ZA axis.

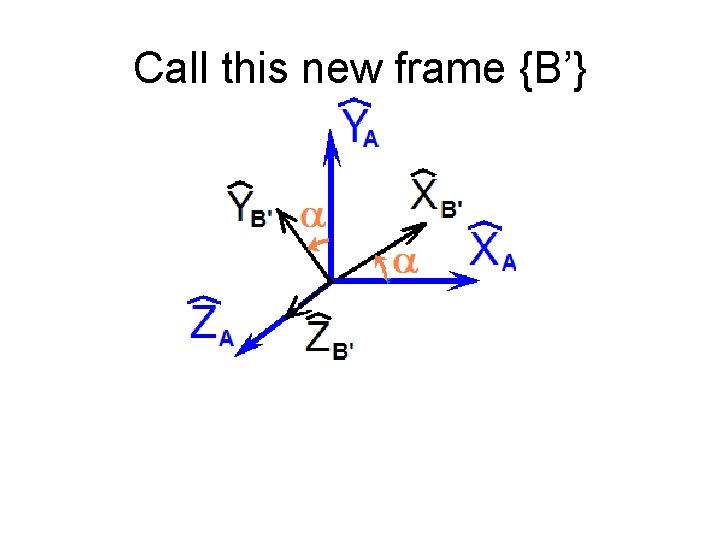
Call this new frame {B’}

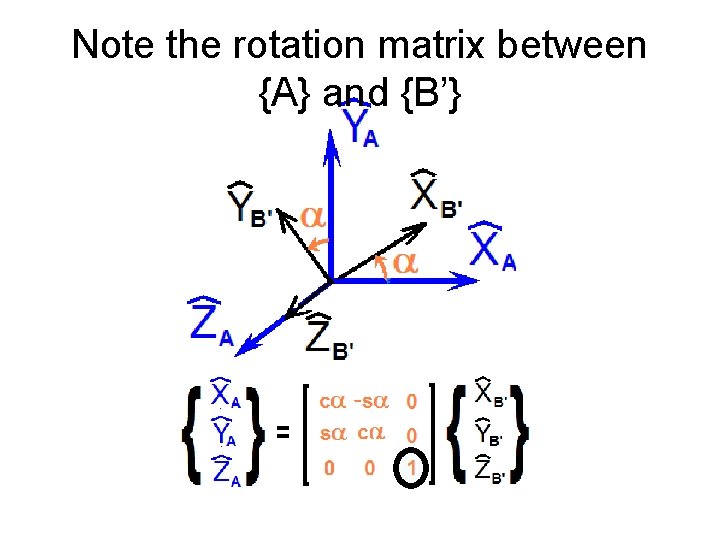
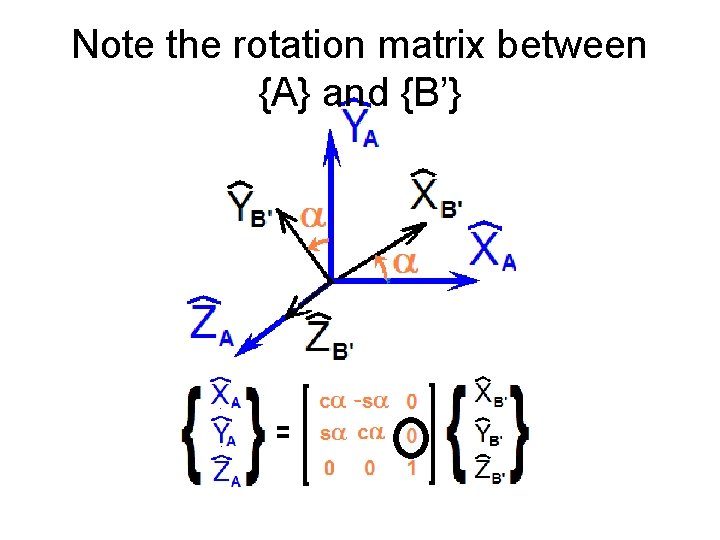
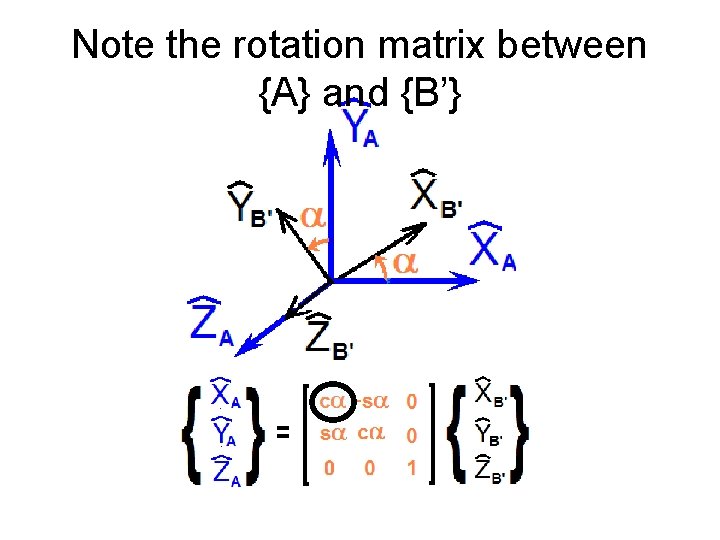
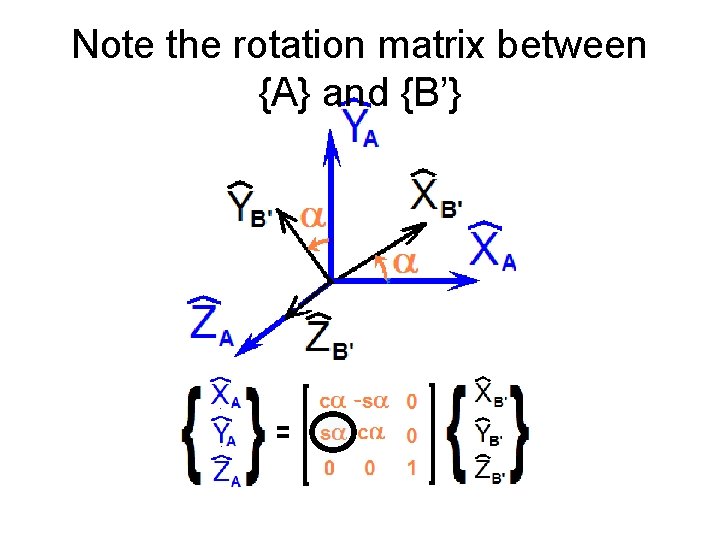
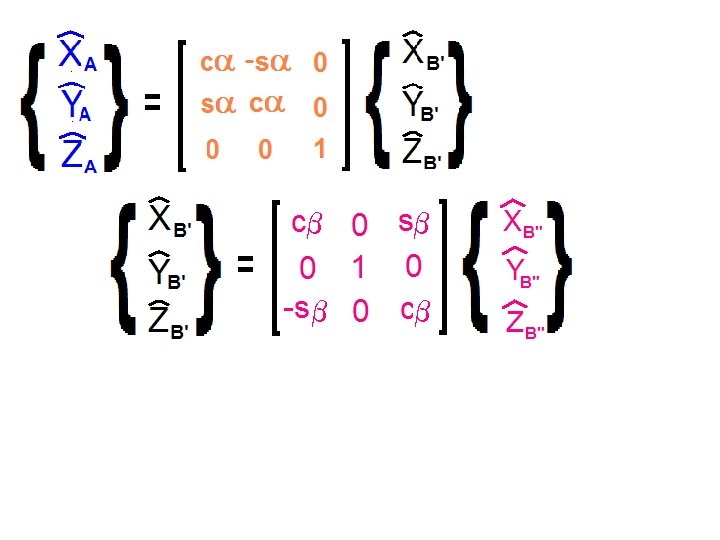
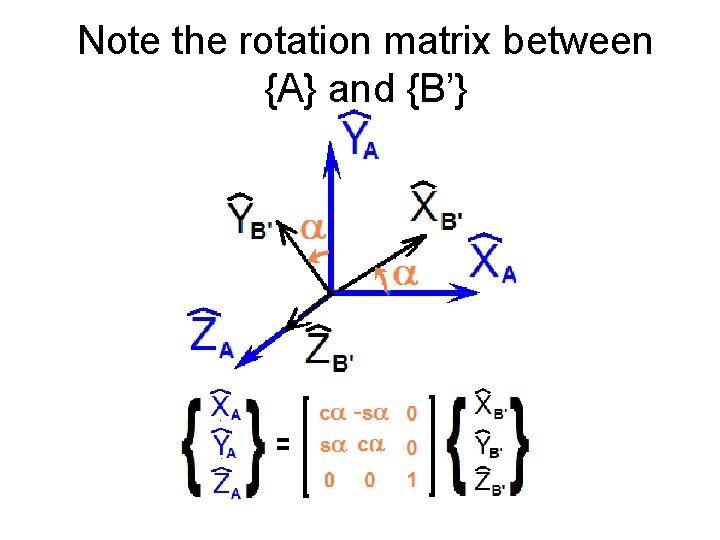
Note the rotation matrix between {A} and {B’}

Note the rotation matrix between {A} and {B’}

Note the rotation matrix between {A} and {B’}

Note the rotation matrix between {A} and {B’}

Note the rotation matrix between {A} and {B’}

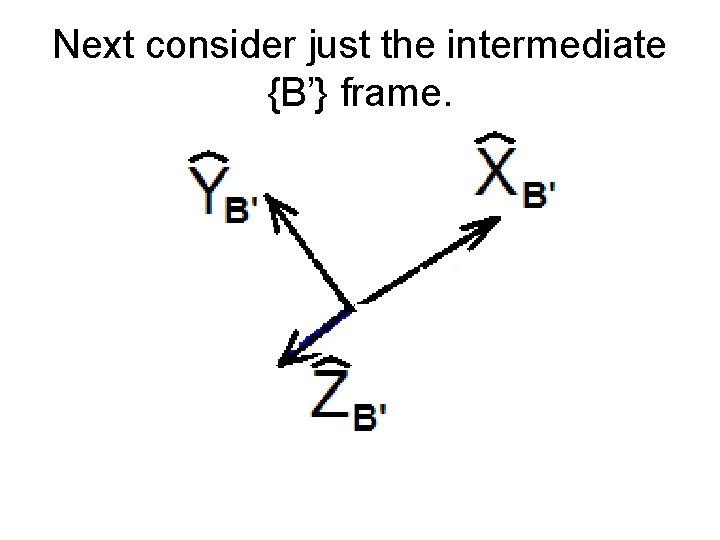
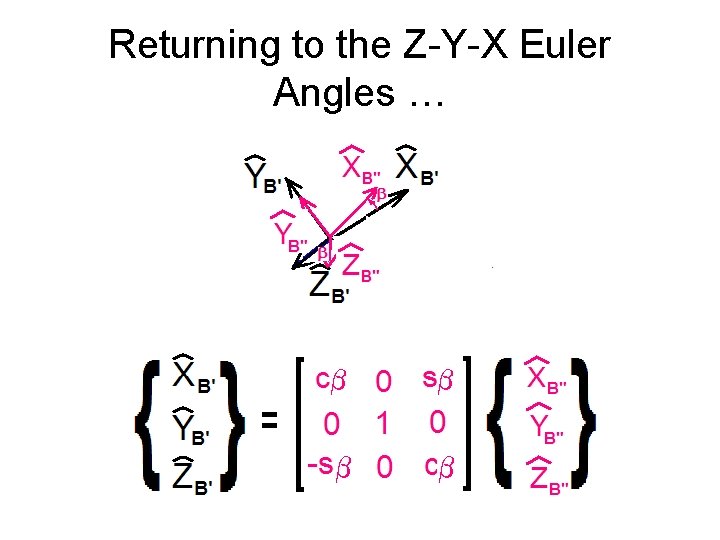
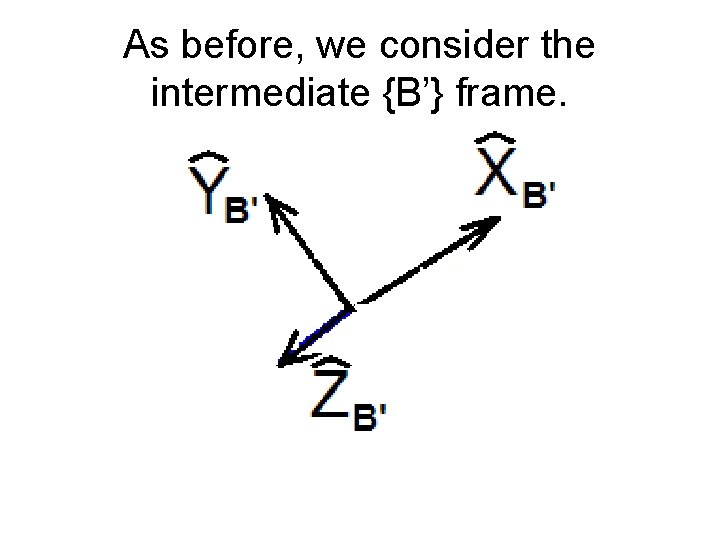
Next consider just the intermediate {B’} frame.

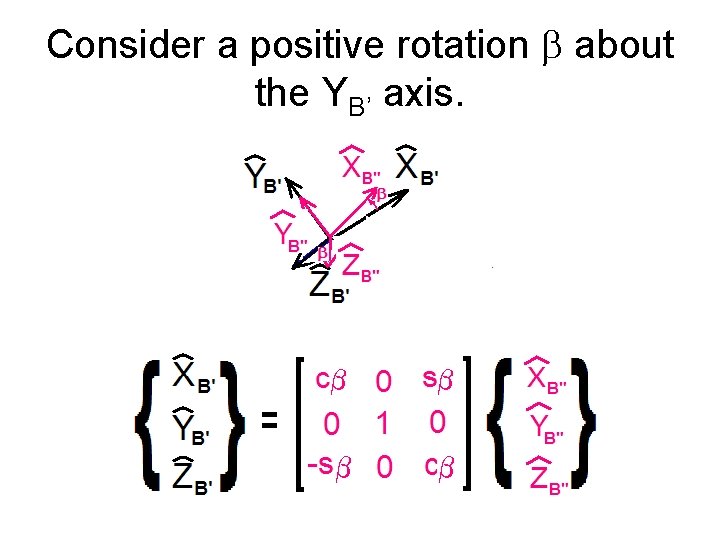
Consider a positive rotation b about the YB’ axis.

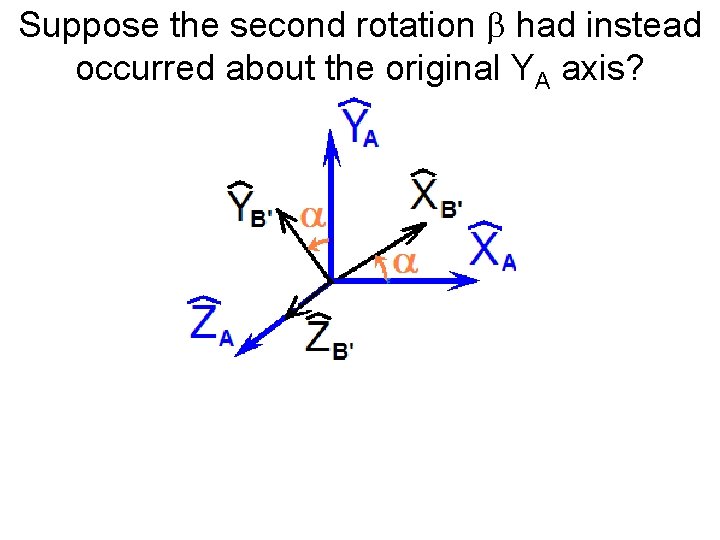
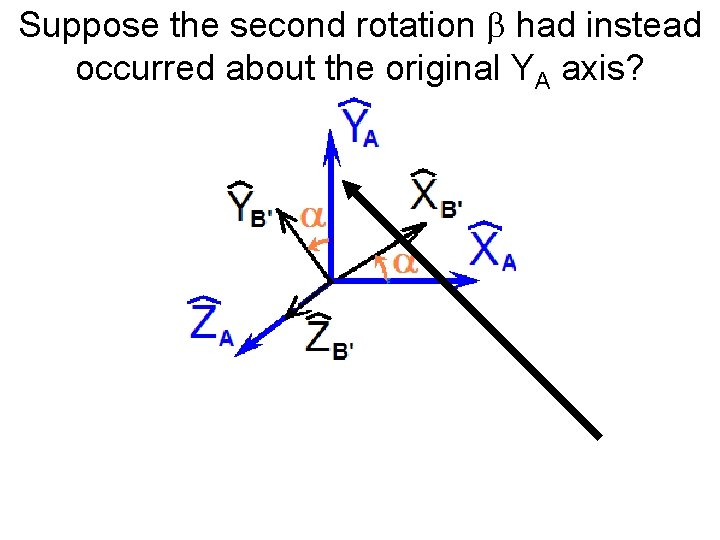
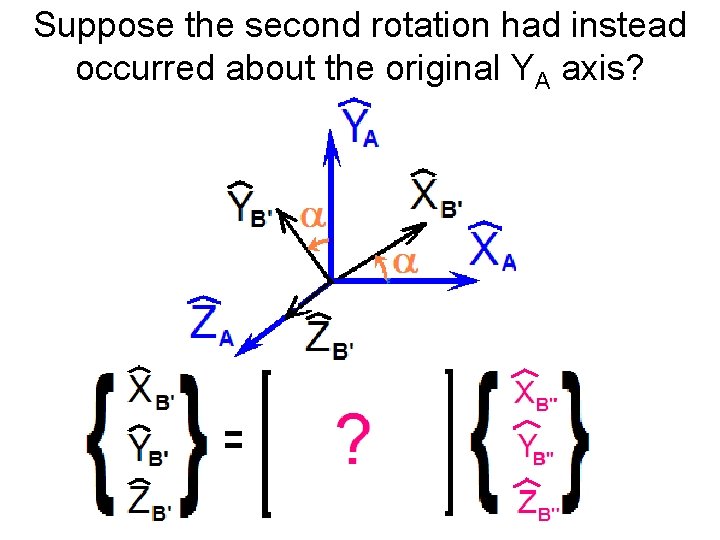
Suppose the second rotation b had instead occurred about the original YA axis?

Suppose the second rotation b had instead occurred about the original YA axis?

Suppose the second rotation had instead occurred about the original YA axis?

Returning to the Z-Y-X Euler Angles …

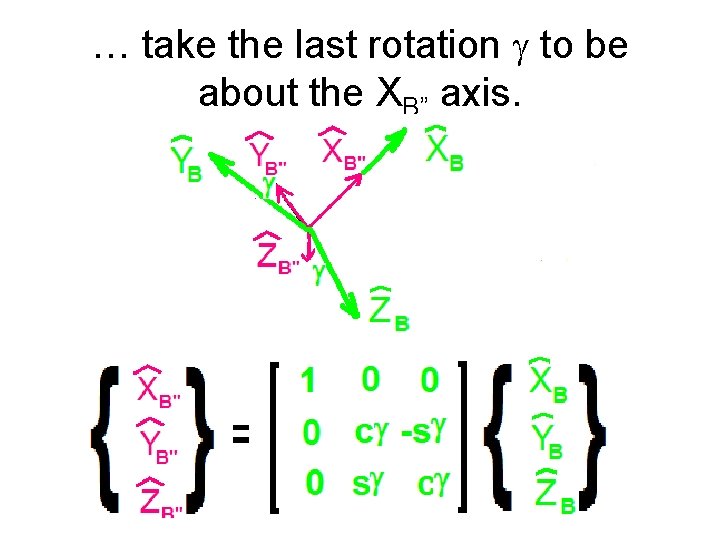
… take the last rotation g to be about the XB” axis.

By following in parallel with Craig’s discussion of ZYX Euler angles, determine the counterpart to Eq. 2. 72, i. e. the 3 x 3 overall rotation matrix, but this time using Z-X-Z Euler angles. Keep the notation a b g for the first, second, third rotations, respectively.

Beginning with the {A} frame, rotate a positive a about the ZA axis.

Note the rotation matrix between {A} and {B’}

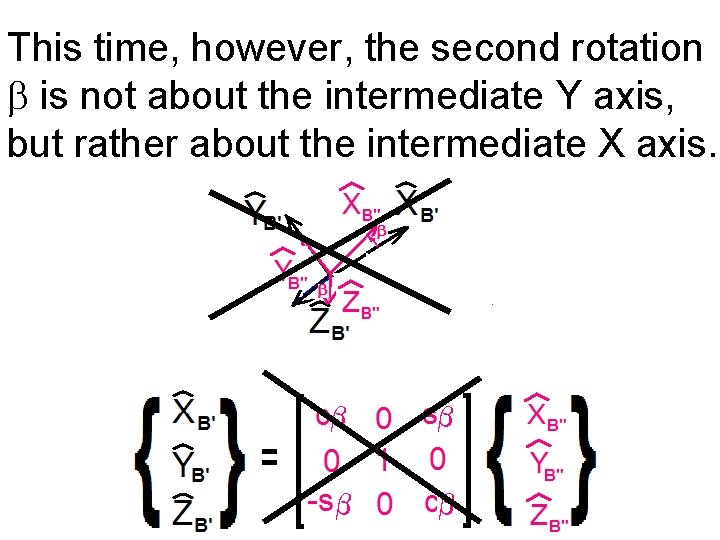
As before, we consider the intermediate {B’} frame.

This time, however, the second rotation b is not about the intermediate Y axis, but rather about the intermediate X axis.

Craig, problem 2. 38: Imagine to unit vectors v 1 and v 2 embedded in a rigid body. Note that, no matter how the body is rotated, the geometric angle between these two vectors is preserved (i. e. rigid-body rotation is an “angle-preserving” operation). Use this fact to give a concise (four or five line) proof that the inverse of a rotation matrix must equal its transpose and that a rotation matrix is orthonormal.