Eulerizing Graph Ch 5 Euler Circuit and Euler

Eulerizing Graph Ch 5

Euler Circuit and Euler path • When a graph has no vertices of odd degree, then it has at least one Euler circuit. • When a graph has exactly two vertices of odd degree, then it has at least one Euler path. • When a graph has more than two vertices of odd degree, then – There is no Euler circuit or Euler path – There is no possible way that we can travel along all the edges of the graph without having to recross some of them.

Euler circuit & Euler path • How we will find a route that covers all the edges of the graph while revisiting the least possible number of edges (deadhead travel)? • In real-world problems, The cost is proportional to the amount of travel. • Total cost of a route = cost of traveling original edges in the graph + cost of deadhead travel

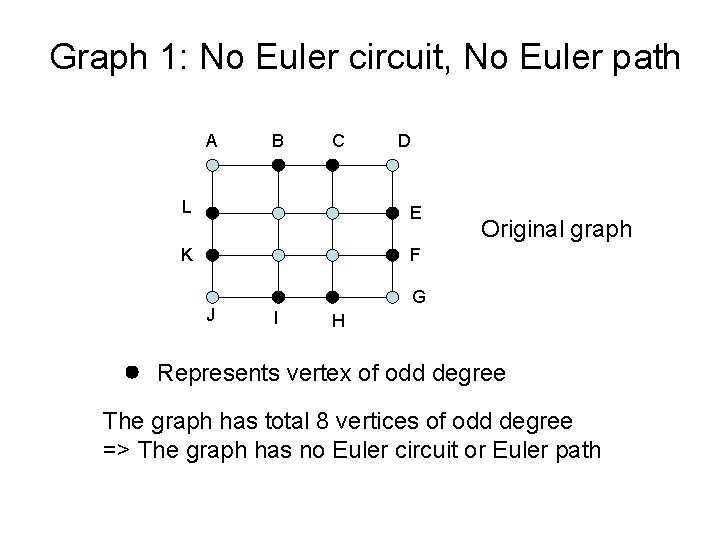
Graph 1: No Euler circuit, No Euler path A B C D L E K F J Original graph G I H Represents vertex of odd degree The graph has total 8 vertices of odd degree => The graph has no Euler circuit or Euler path

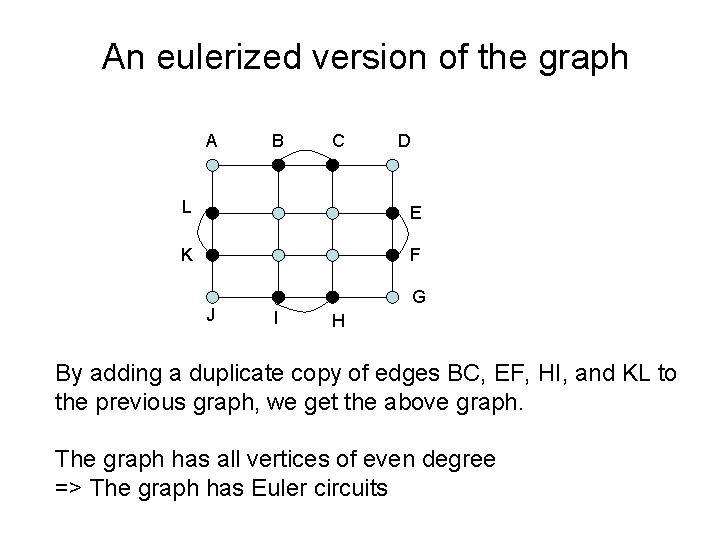
An eulerized version of the graph A B C D L E K F J G I H By adding a duplicate copy of edges BC, EF, HI, and KL to the previous graph, we get the above graph. The graph has all vertices of even degree => The graph has Euler circuits

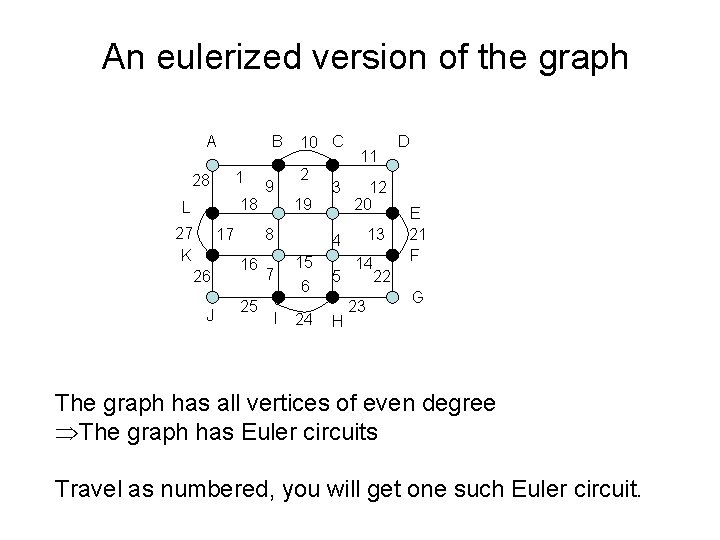
An eulerized version of the graph A B 1 28 9 18 L 27 K 17 26 J 10 C 2 19 8 16 25 7 I 3 11 12 20 13 4 15 6 24 5 H 14 23 D E 21 F 22 G The graph has all vertices of even degree ÞThe graph has Euler circuits Travel as numbered, you will get one such Euler circuit.

Trip along the edges of our original graph A 28 B 1 9 18 L 27, 17 K 26 J 2, 10 19 8 16 25 7 I C 3 11 12 20 4 15 6, 24 5 H 14 23 D E 13, 21 F 22 G In this trip we are traveling along all of the edges of the graph, but we are retracing four of them: BC, EF, HI, and KL. This is not an Euler circuit for the original graph, it is a circuit describing the most efficient trip – an optimal circuit.

Eulerizing a graph • We have started with a graph • Modifying it by adding extra edges in such a way that the odd vertices become even vertices. • The process of changing a graph by adding additional edges so that odd vertices are eliminated is called eulerizing the graph. • Note: The edges that we add must be duplicates of edges that already exist. The idea is to cover the edges of the original graph in the best possible way without creating any new.

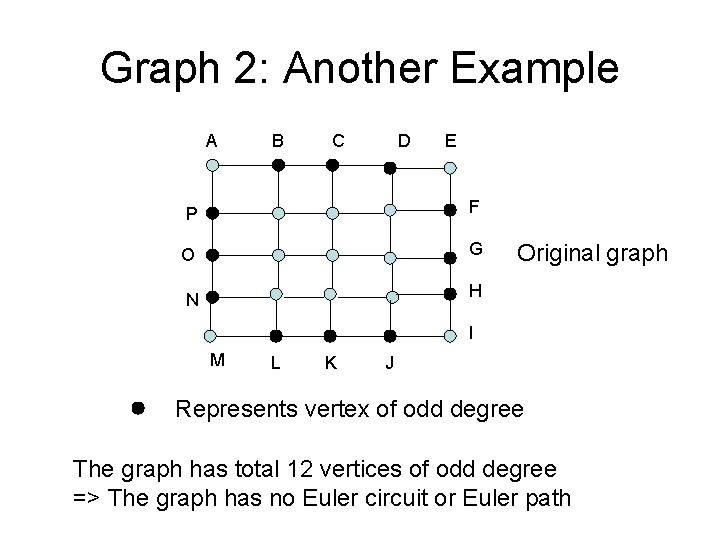
Graph 2: Another Example A B C D E P F O G N H Original graph I M L K J Represents vertex of odd degree The graph has total 12 vertices of odd degree => The graph has no Euler circuit or Euler path

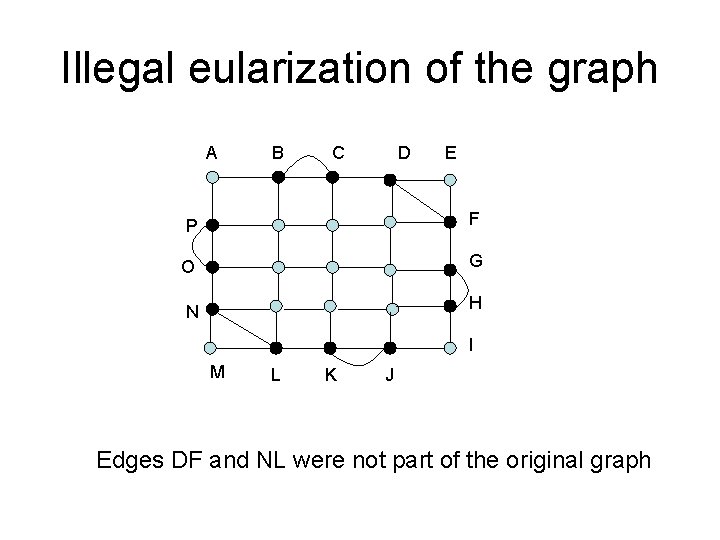
Illegal eularization of the graph A B C D E P F O G N H I M L K J Edges DF and NL were not part of the original graph

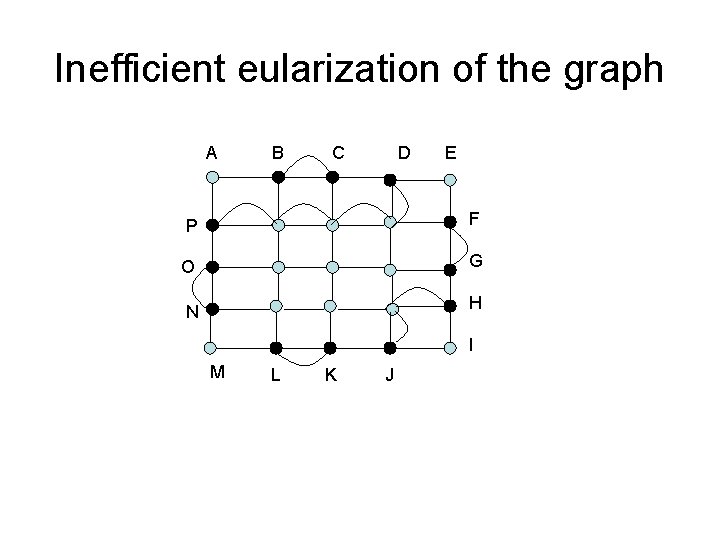
Inefficient eularization of the graph A B C D E P F O G N H I M L K J

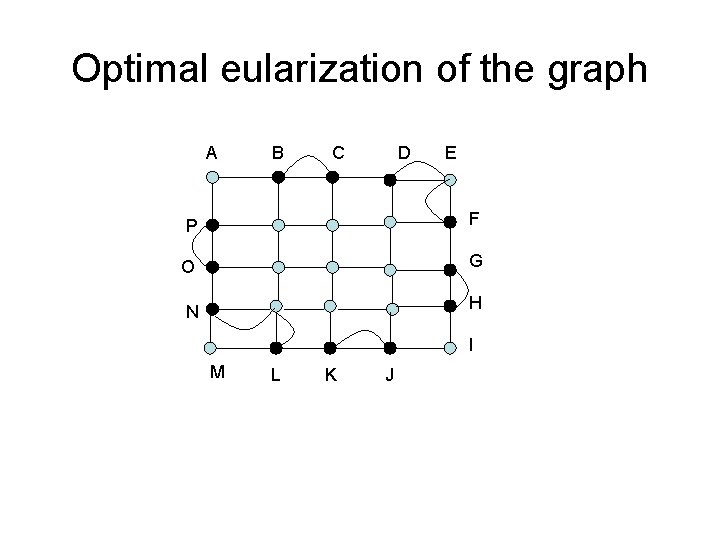
Optimal eularization of the graph A B C D E P F O G N H I M L K J

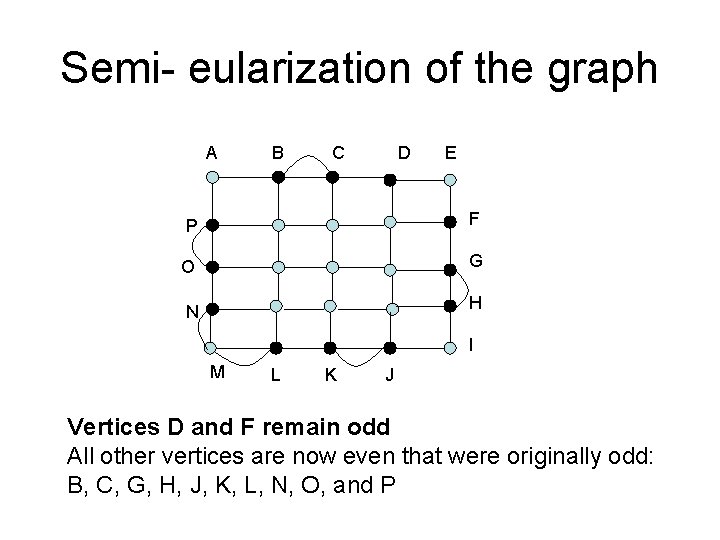
Semi- eularization of the graph • We are not required to start and end at the same vertex. • We duplicate as many edges as needed to eliminate all odd vertices except for two, which we allow to remain odd. • We then use one of the odd vertices as the starting point and we will end up to the other odd vertex.

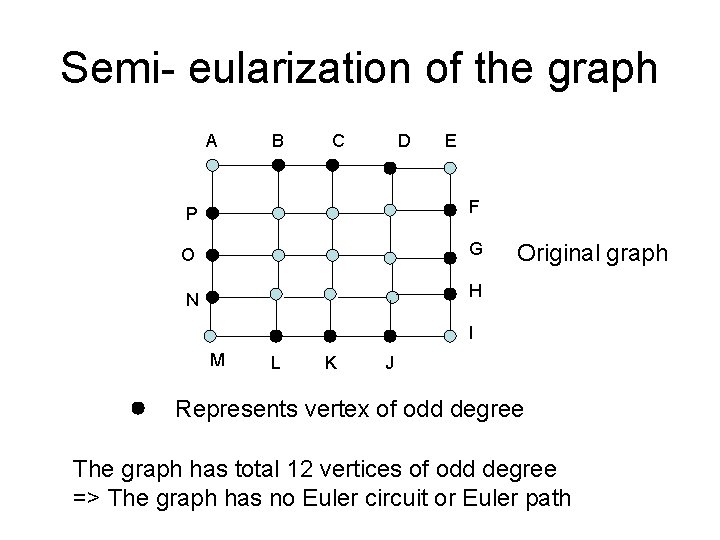
Semi- eularization of the graph A B C D E P F O G N H Original graph I M L K J Represents vertex of odd degree The graph has total 12 vertices of odd degree => The graph has no Euler circuit or Euler path

Semi- eularization of the graph A B C D E P F O G N H I M L K J Vertices D and F remain odd All other vertices are now even that were originally odd: B, C, G, H, J, K, L, N, O, and P

Semi-eularization of the graph • Semi-eularization tells us that is possible to travel all the edges of the graph by starting at D and ending at F (or vice versa) and • duplicating only six of the edges: BC, GH, JK, LM, MN, and OP • There are many other ways to accomplish this, but none of them can do with fewer than 6 duplicate edges.