Discrete Math and Management Science Why is Discrete

Discrete Math and Management Science Why is Discrete Math important? http: //hsor. org/what_is_or. cfm http: //hsor. org/case_studies. cfm

Chapter 1: Urban Services Management Science • Management Science – Uses mathematical methods to help find optimal solutions to management problems. Often called Operations Research. • Optimal Solutions — The best (most favorable) solution – Government, business, and individuals all seek optimal results. n Optimization problems: Finish a job quickly q Maximize profits q Minimize costs q n Urban Services to optimize: Checking parking meters q Delivering mail q Removing snow q 2

What is a routing problem? How to deliver goods/services to an assortment of destinations the most efficient way. (best, cheapest, shortest route) This problem comes up in many areas: transportation, communications, and delivery services to name a few.

Examples • Mail delivery • Garbage collection • Police patrols • Most importantly – late night pizza deliveries

For instance, it is very important for airlines to efficiently schedule flights among the cities served by the airline. Putting together efficient airline schedules is a routing problem.

We will study two classes of routing problems 1. Graph Theory and Euler circuit problems. (this chapter) 2. Hamilton circuit problem. (the next chapter)

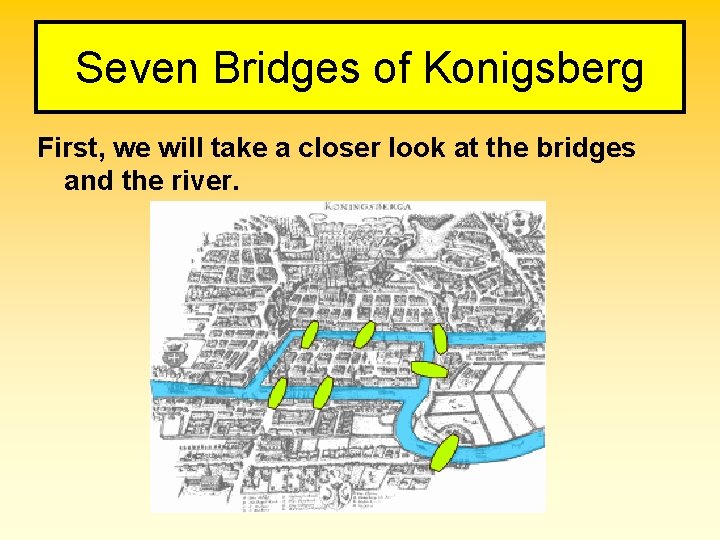
Once upon a time……. . • There is a town in Russia whose name today is Kaliningrad. • In the 1700 s, it was in Prussia and its name was Königsberg. • Here's a true story. • Once upon a time (OK, in the 18 th century), in a place far away (well, Prussia), there once was a town called Königsberg. The townspeople enjoyed walking through their town and passing over the bridges spanning the river which passed through town. The city sits along river Pregel, in which there are two large islands. Seven bridges connected the islands to the mainland , as depicted in the following image. The citizens began to wonder if there was a path that would allow them to cross all seven bridges exactly once. Over the years, a controversy arose and eventually word of it reached a very famous mathematician of the time, Leonhard Euler.

Leonhard Euler (1707– 1783) (pronounced “oiler”) Swiss Mathematician Among other discoveries, he was credited with inventing the idea of a graph as well as the concepts of valence and connectedness. Let's reconstruct Euler's solution to the bridge problem.

Seven Bridges of Konigsberg First, we will take a closer look at the bridges and the river.

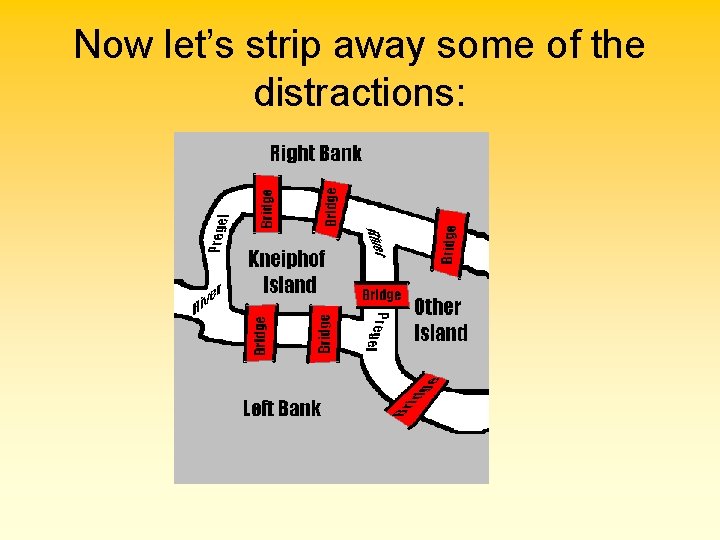
Now let’s strip away some of the distractions:

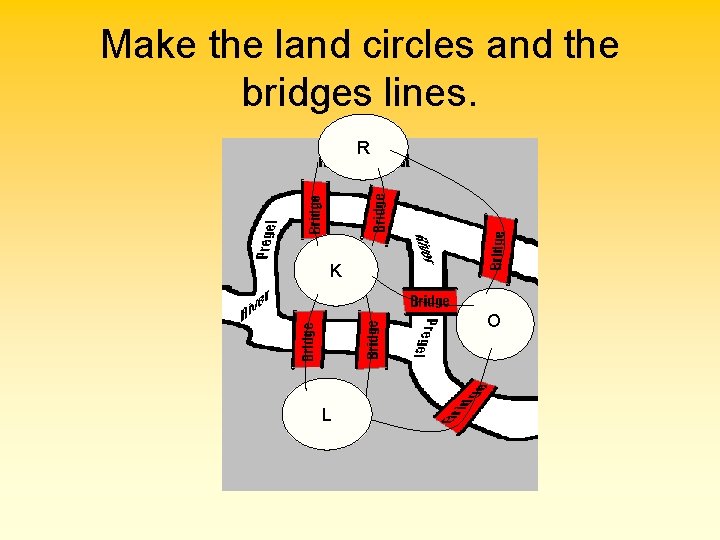
Make the land circles and the bridges lines. R K O L

Simplifying things once again: R K O L

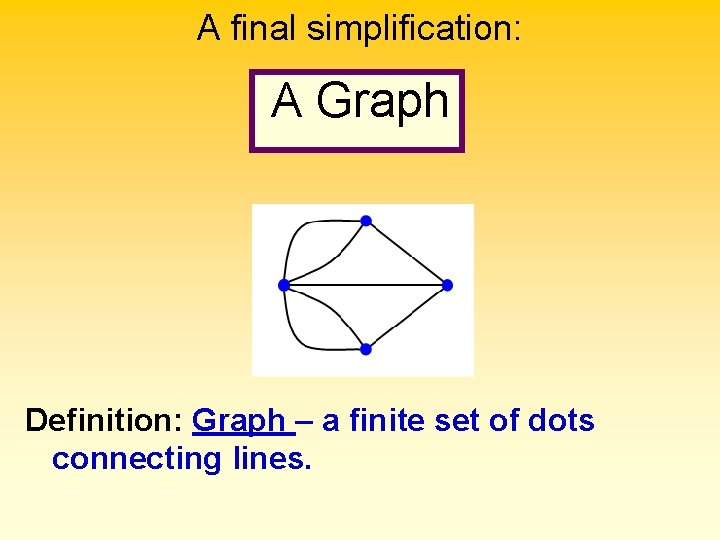
A final simplification: A Graph Definition: Graph – a finite set of dots connecting lines.

Chapter 1: Euler Circuits Outline/learning Objectives ØTo understand the meaning of basic graph terminology. ØTo identify and model Euler circuit and path problems. ØTo eulerize a graph when necessary

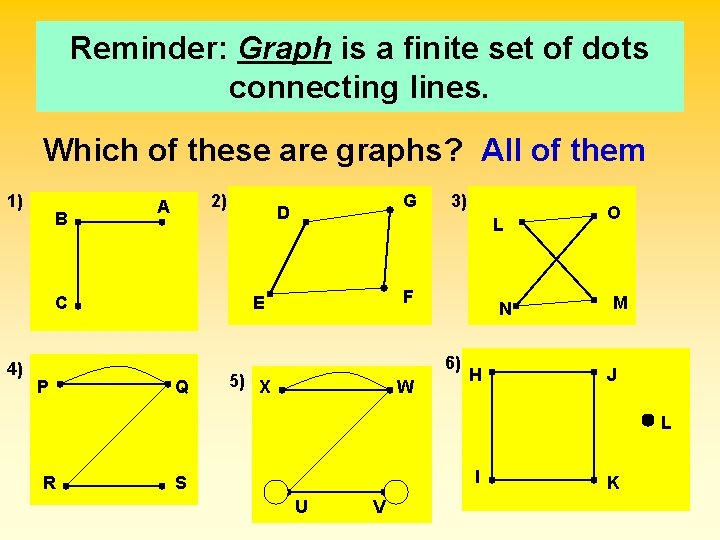
Reminder: Graph is a finite set of dots connecting lines. Which of these are graphs? All of them 1) B 2) A C 4) P G D L F E Q 3) N 6) 5) X W H O M J L R I S U V KK

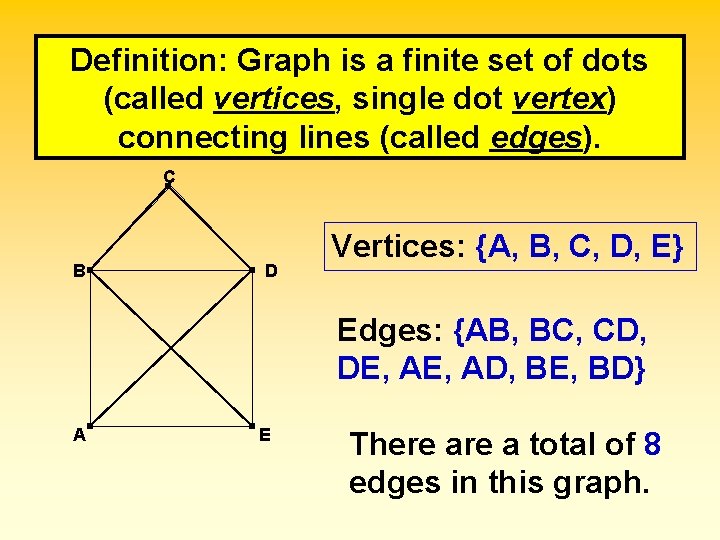
Definition: Graph is a finite set of dots (called vertices, single dot vertex) connecting lines (called edges). C B D Vertices: {A, B, C, D, E} Edges: {AB, BC, CD, DE, AD, BE, BD} A E There a total of 8 edges in this graph.

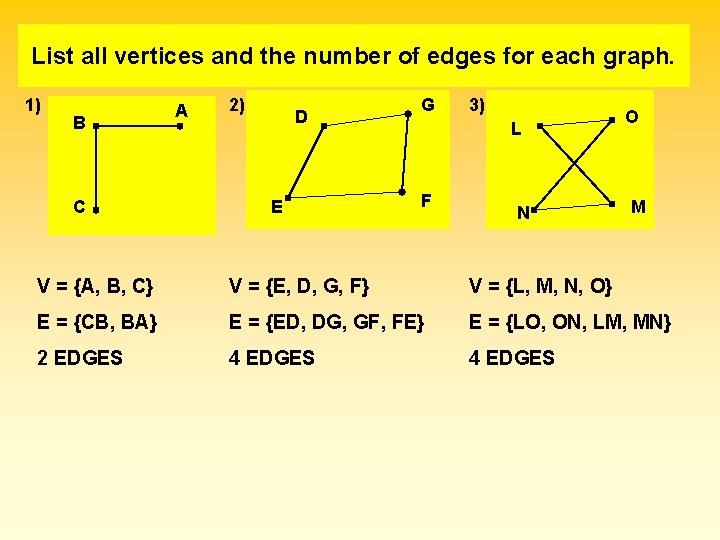
List all vertices and the number of edges for each graph. 1) B C A 2) D E G 3) L F N O M V = {A, B, C} V = {E, D, G, F} V = {L, M, N, O} E = {CB, BA} E = {ED, DG, GF, FE} E = {LO, ON, LM, MN} 2 EDGES 4 EDGES

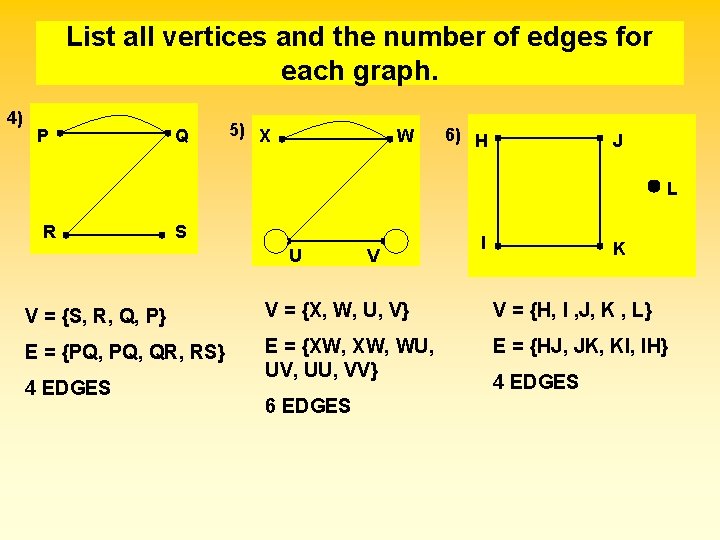
List all vertices and the number of edges for each graph. 4) P Q 5) X W 6) H J L R S U V I K V = {S, R, Q, P} V = {X, W, U, V} V = {H, I , J, K , L} E = {PQ, QR, RS} E = {XW, WU, UV, UU, VV} E = {HJ, JK, KI, IH} 4 EDGES 6 EDGES 4 EDGES

Homework • p 20 5, 8 • p 22 3, 9 (page 7 is figure 1. 6)

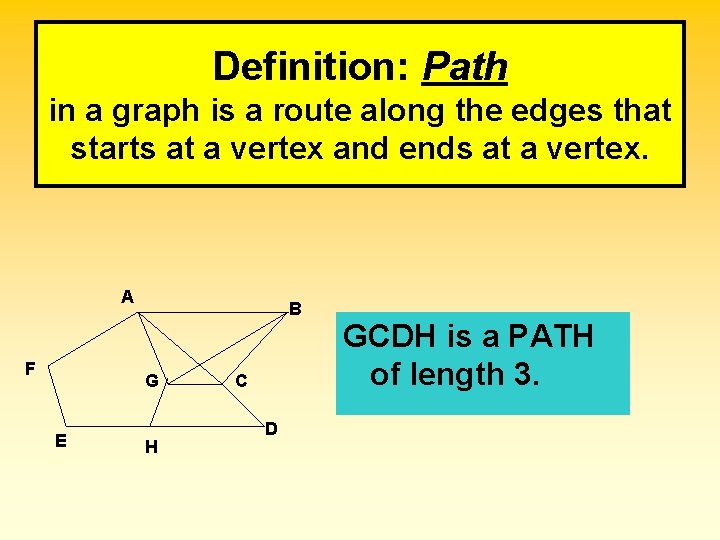
Definition: Path in a graph is a route along the edges that starts at a vertex and ends at a vertex. A F B G E H C D GCDH is a PATH of length 3.

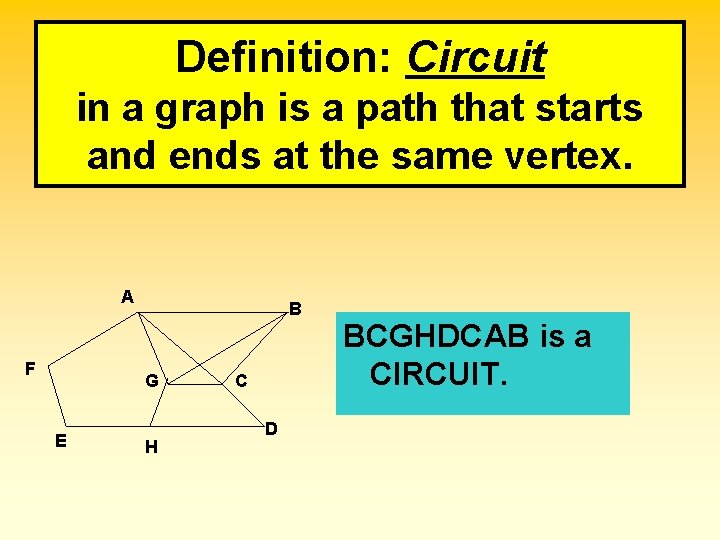
Definition: Circuit in a graph is a path that starts and ends at the same vertex. A F B G E H C D BCGHDCAB is a CIRCUIT.

Path vs. Circuit q Paths – Paths can start and end at any vertex using the edges given. Examples: NLB, NMRB, or if you moved from New York to London q Circuits – Paths that starts and ends at the same vertex. Examples: MRLM, LRBL, or if you took a vacation to London Nonstop air routes 22

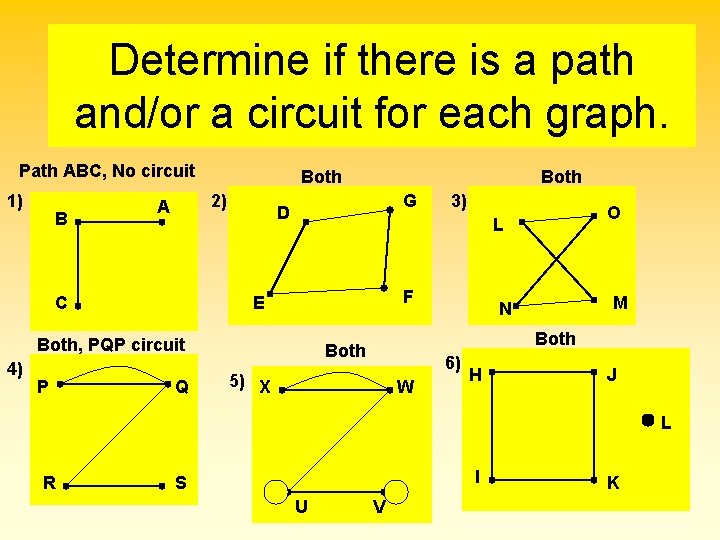
Determine if there is a path and/or a circuit for each graph. Path ABC, No circuit 1) B Both 2) A C G D P F E Q 3) O L Both, PQP circuit 4) Both M N Both 6) 5) X W H J L R I S U V KK

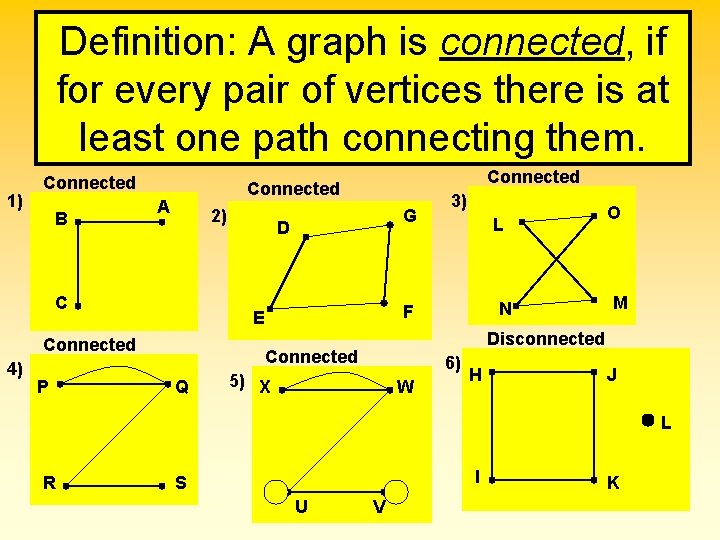
Definition: A graph is connected, if for every pair of vertices there is at least one path connecting them. 1) Connected B A 2) C P G D O L M N Disconnected Connected Q 3) F E Connected 4) Connected 6) 5) X W H J L R I S U V KK

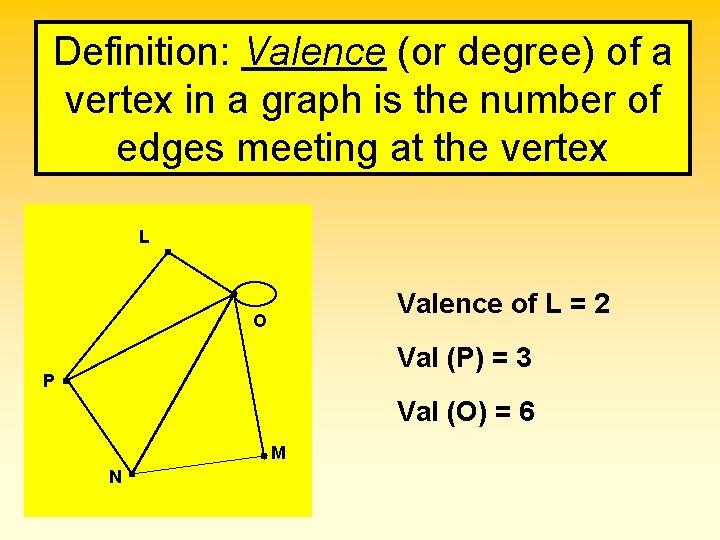
Definition: Valence (or degree) of a vertex in a graph is the number of edges meeting at the vertex L Valence of L = 2 O Val (P) = 3 P Val (O) = 6 M N

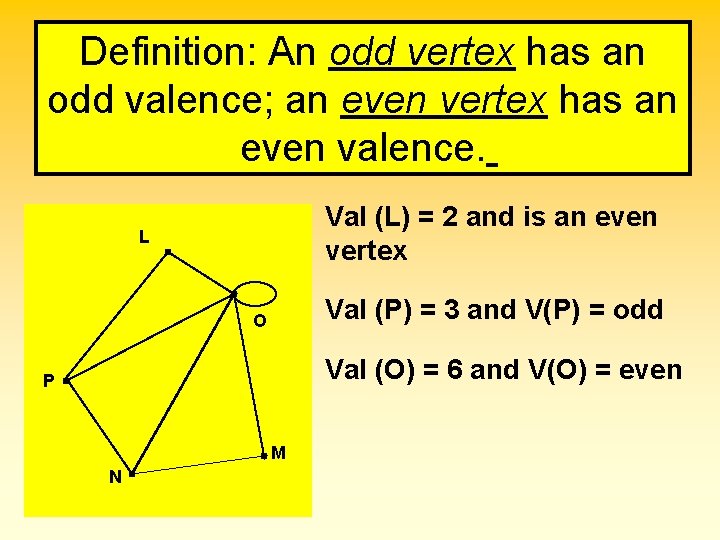
Definition: An odd vertex has an odd valence; an even vertex has an even valence. Val (L) = 2 and is an even vertex L Val (P) = 3 and V(P) = odd O Val (O) = 6 and V(O) = even P M N

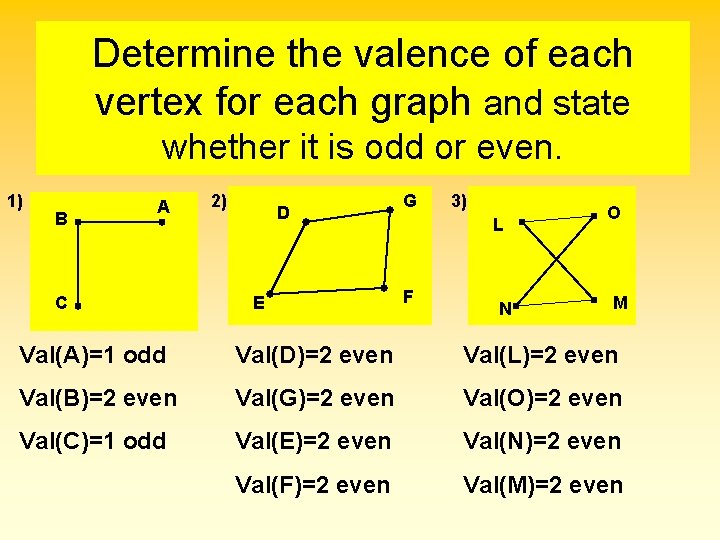
Determine the valence of each vertex for each graph and state whether it is odd or even. 1) B A C 2) D E G 3) L F N O M Val(A)=1 odd Val(D)=2 even Val(L)=2 even Val(B)=2 even Val(G)=2 even Val(O)=2 even Val(C)=1 odd Val(E)=2 even Val(N)=2 even Val(F)=2 even Val(M)=2 even

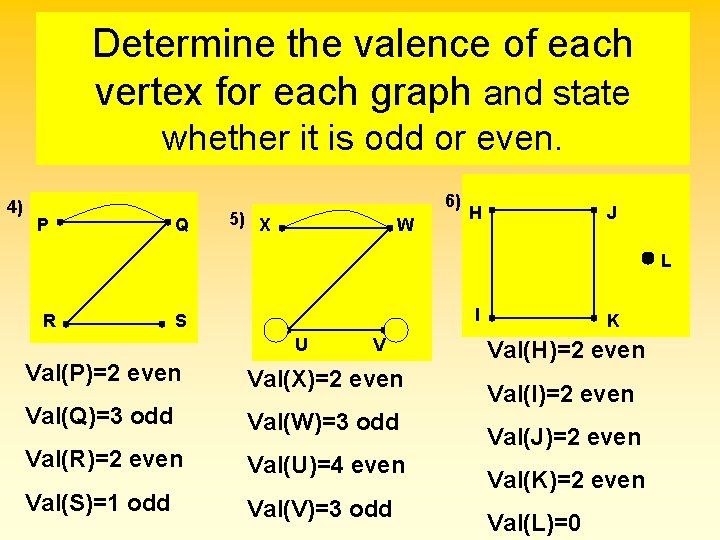
Determine the valence of each vertex for each graph and state whether it is odd or even. 4) P Q 6) 5) X W H J L R I S U V Val(P)=2 even Val(X)=2 even Val(Q)=3 odd Val(W)=3 odd Val(R)=2 even Val(U)=4 even Val(S)=1 odd Val(V)=3 odd K Val(H)=2 even Val(I)=2 even Val(J)=2 even Val(K)=2 even Val(L)=0

Classwork/Homework • p 20

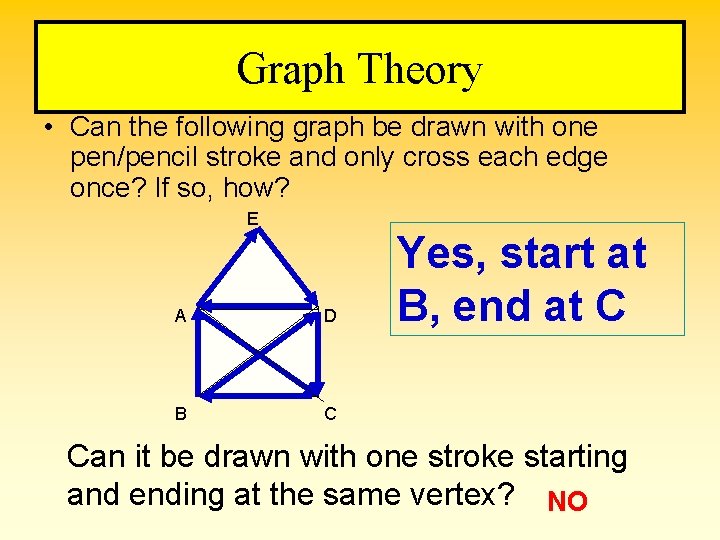
Graph Theory • Can the following graph be drawn with one pen/pencil stroke and only cross each edge once? If so, how? E A D B C Yes, start at B, end at C Can it be drawn with one stroke starting and ending at the same vertex? NO

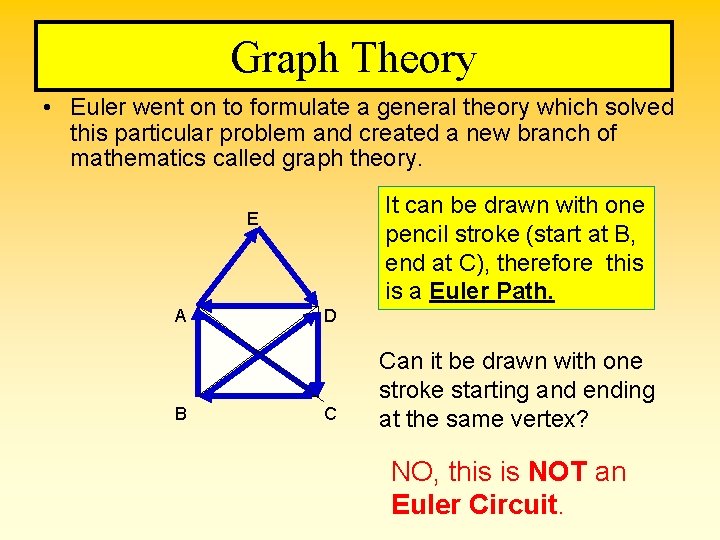
Graph Theory • Euler went on to formulate a general theory which solved this particular problem and created a new branch of mathematics called graph theory. It can be drawn with one pencil stroke (start at B, end at C), therefore this is a Euler Path. E A B D C Can it be drawn with one stroke starting and ending at the same vertex? NO, this is NOT an Euler Circuit.

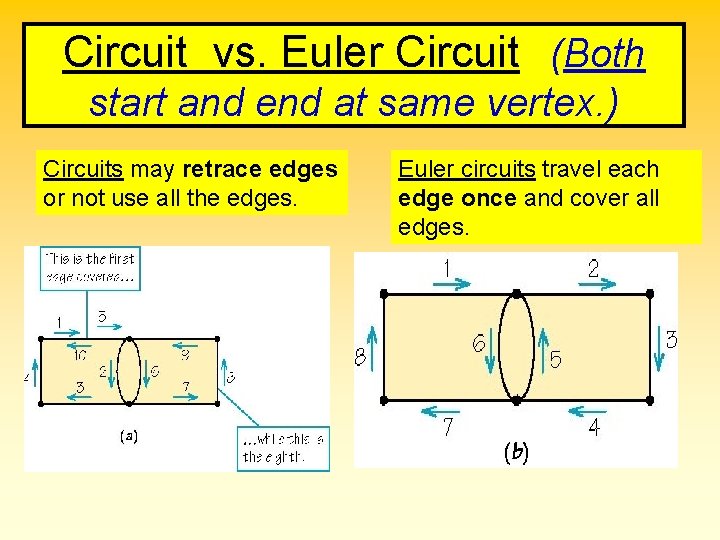
Circuit vs. Euler Circuit (Both start and end at same vertex. ) Circuits may retrace edges or not use all the edges. Euler circuits travel each edge once and cover all edges.

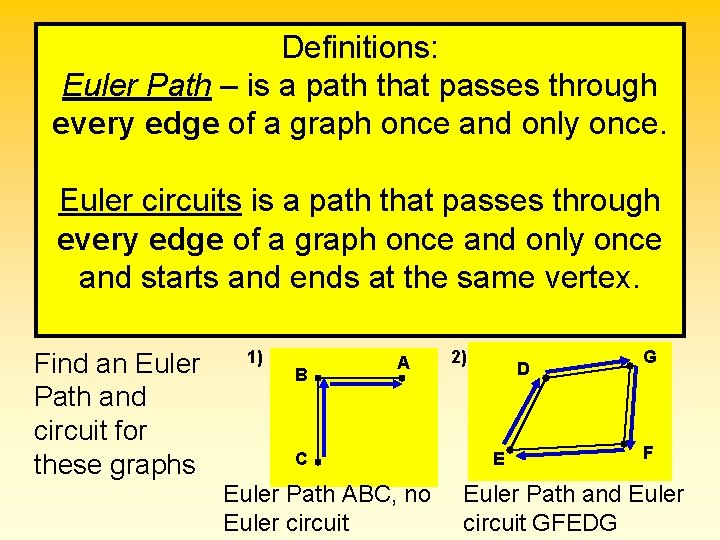
Definitions: Euler Path – is a path that passes through every edge of a graph once and only once. Euler circuits is a path that passes through every edge of a graph once and only once and starts and ends at the same vertex. Find an Euler Path and circuit for these graphs 1) B A C Euler Path ABC, no Euler circuit 2) D E G F Euler Path and Euler circuit GFEDG

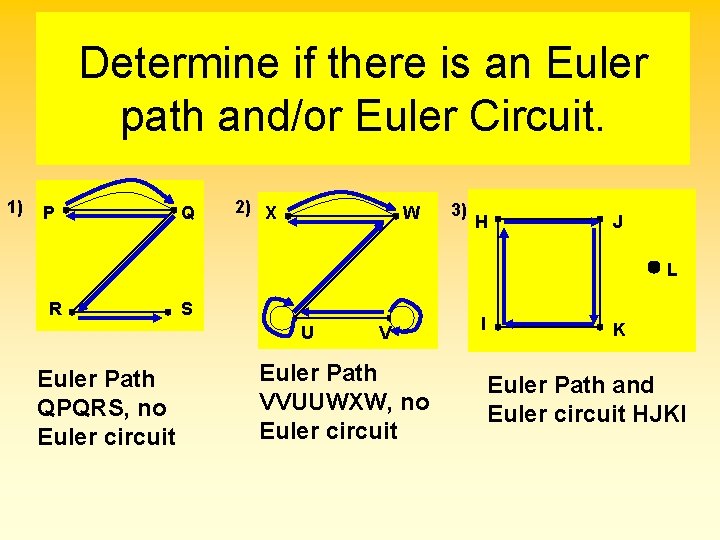
Determine if there is an Euler path and/or Euler Circuit. 1) P Q 2) X W 3) H J L R S U Euler Path QPQRS, no Euler circuit V Euler Path VVUUWXW, no Euler circuit I K Euler Path and Euler circuit HJKI

Two Ways to Find an Euler Circuit q. Trial and error Keep trying to create different paths to find one that starts and ends at the same point and does not retrace steps. q. Mathematical approach (better method) Euler’s Theorem: An Euler circuit exists if the following statements are true: ØAll vertices have even valence. ØThe graph is connected.

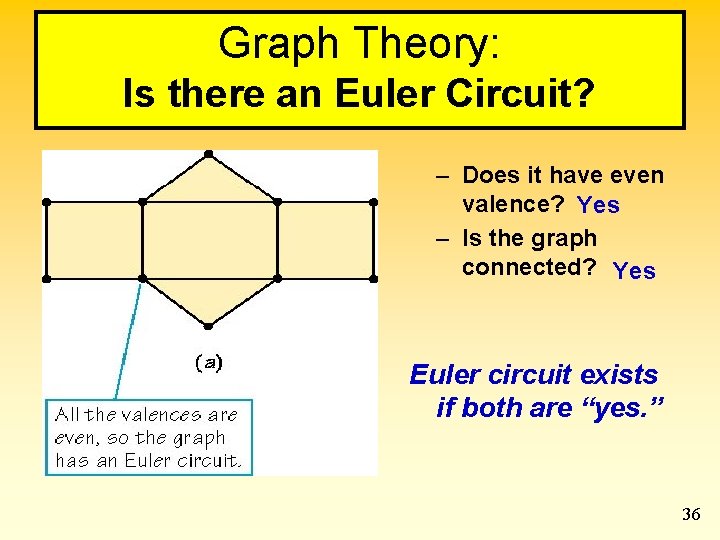
Graph Theory: Is there an Euler Circuit? – Does it have even valence? Yes – Is the graph connected? Yes Euler circuit exists if both are “yes. ” 36

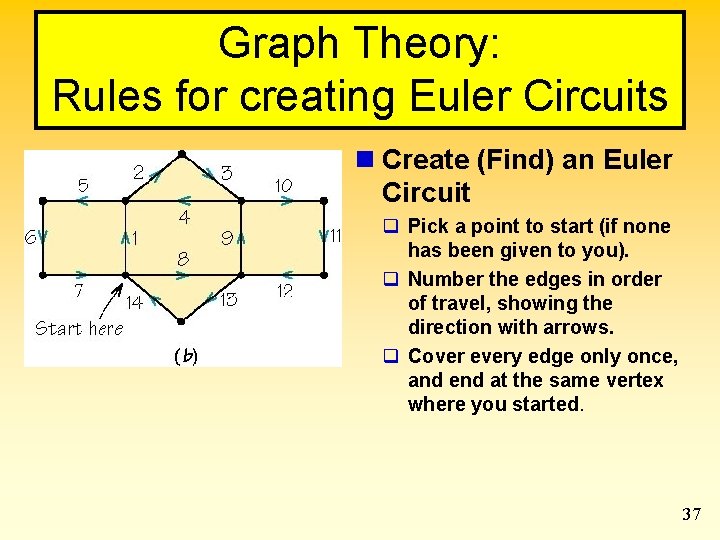
Graph Theory: Rules for creating Euler Circuits n Create (Find) an Euler Circuit q Pick a point to start (if none has been given to you). q Number the edges in order of travel, showing the direction with arrows. q Cover every edge only once, and end at the same vertex where you started. 37

Beyond Euler Circuits • Chinese Postman Problem – In real life, not all problems will be perfect Euler circuits. – What do you do if there are odd valences? – Chinese mathematician Meigu Guan first studied this problem in 1962, hence the name. The blue dots indicate parking meters along the street. The graph represents edges with parking meters. Notice only vertices 38 C and G have odd valence.

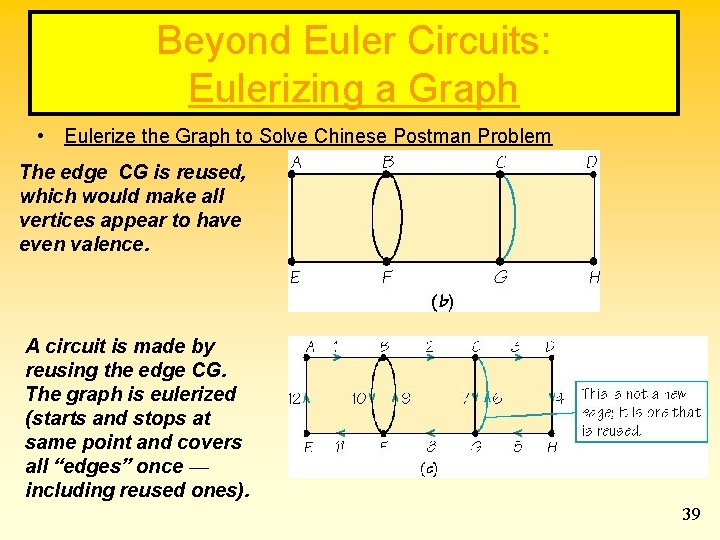
Beyond Euler Circuits: Eulerizing a Graph • Eulerize the Graph to Solve Chinese Postman Problem The edge CG is reused, which would make all vertices appear to have even valence. A circuit is made by reusing the edge CG. The graph is eulerized (starts and stops at same point and covers all “edges” once — including reused ones). 39

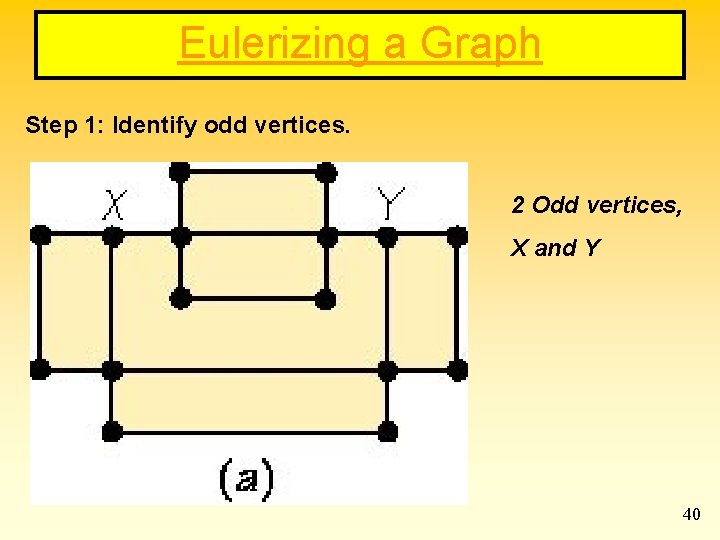
Eulerizing a Graph Step 1: Identify odd vertices. 2 Odd vertices, X and Y 40

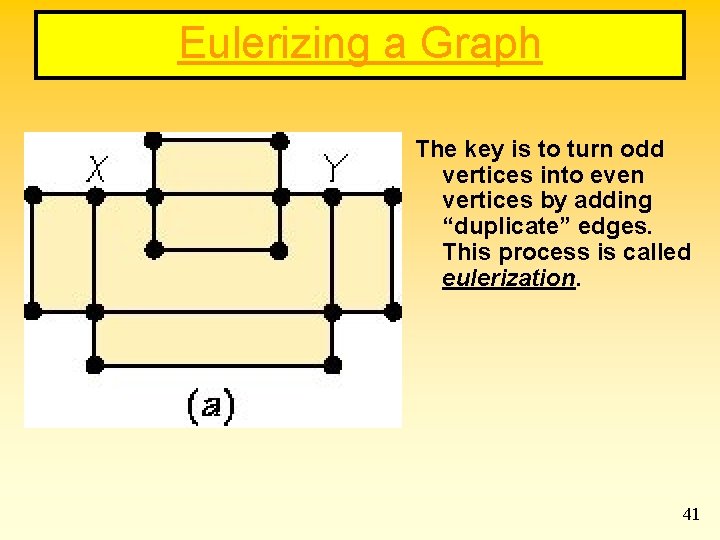
Eulerizing a Graph The key is to turn odd vertices into even vertices by adding “duplicate” edges. This process is called eulerization. 41

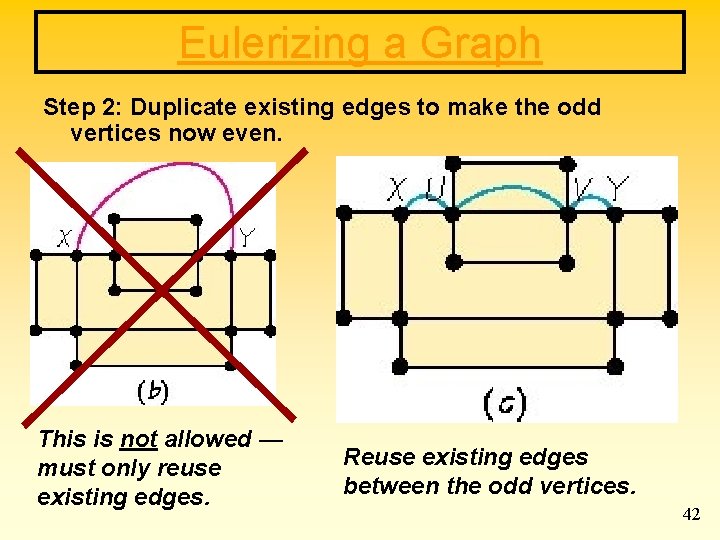
Eulerizing a Graph Step 2: Duplicate existing edges to make the odd vertices now even. This is not allowed — must only reuse existing edges. Reuse existing edges between the odd vertices. 42

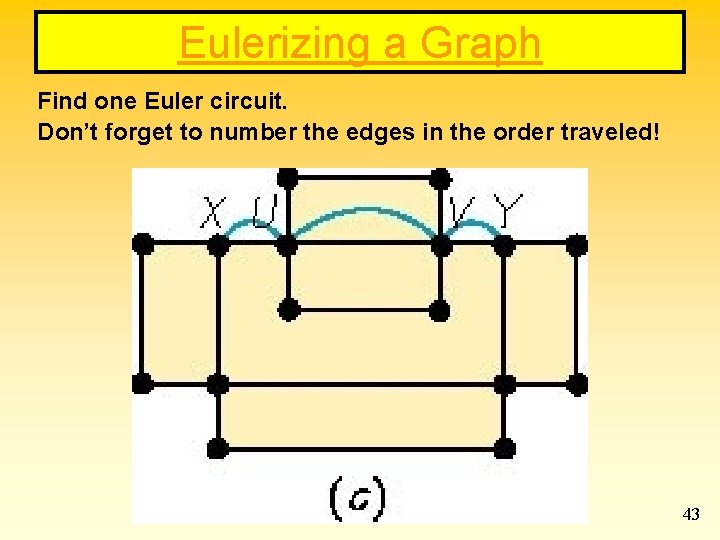
Eulerizing a Graph Find one Euler circuit. Don’t forget to number the edges in the order traveled! 43

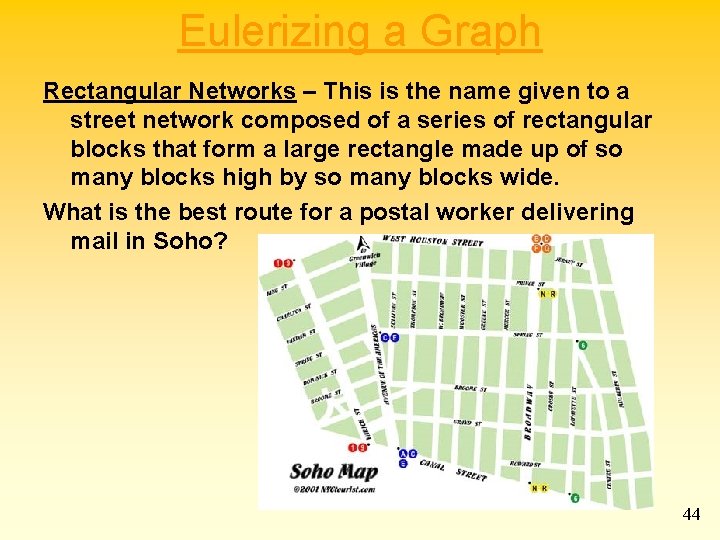
Eulerizing a Graph Rectangular Networks – This is the name given to a street network composed of a series of rectangular blocks that form a large rectangle made up of so many blocks high by so many blocks wide. What is the best route for a postal worker delivering mail in Soho? 44

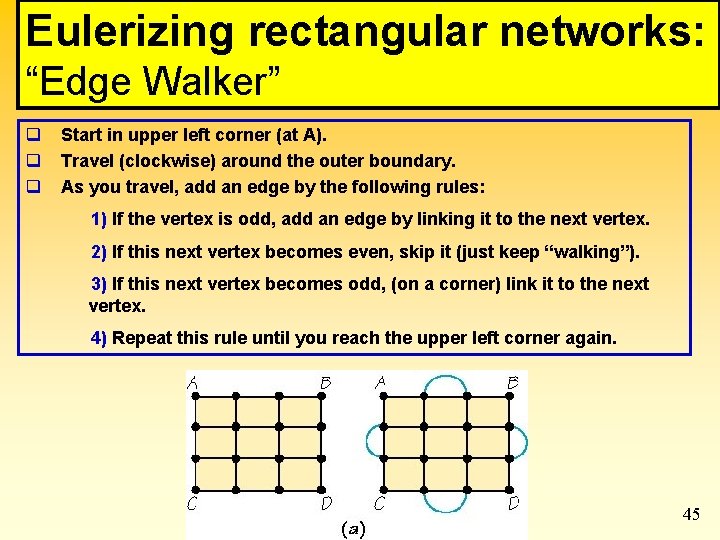
Eulerizing rectangular networks: “Edge Walker” q q q Start in upper left corner (at A). Travel (clockwise) around the outer boundary. As you travel, add an edge by the following rules: 1) If the vertex is odd, add an edge by linking it to the next vertex. 2) If this next vertex becomes even, skip it (just keep “walking”). 3) If this next vertex becomes odd, (on a corner) link it to the next vertex. 4) Repeat this rule until you reach the upper left corner again. 45