Mthodes et Algorithmes Graphiques Ian Jermyn 2 Quelques

Méthodes et Algorithmes Graphiques Ian Jermyn

2 Quelques points avant de commencer. n Pour me contacter: Ian Jermyn. n Ian. Jermyn@sophia. inria. fr. n www-sop. inria. fr/ariana/personnel/Ian. Jermyn. n Nationalité: Britannique. n Excusez mon français s’il vous plait. n n Chercheur en traitement d’image et vision par ordinateur à l’INRIA dans projet Ariana. Formation: en physique théorique, puis vision par ordinateur.

3 Quelques points avant de commencer. n N’hésitez pas à: n n Me questionner: c’est la façon meilleure d’apprendre. Demander que: n n n Je parle plus fort. Je répète ou explique quelque chose. Vous pouvez trouver ce fichier à l’URL precedent, sous ‘Teaching/Advising’ puis ‘Courses’, à partir de lundi.

4 But n Donner une structure mathématique afin que vous puissiez: n n Comprendre la littérature. Utiliser ces méthodes pour: n n n Systématiser vos idées. Bien poser les problèmes. Donner des algorithmes flexibles: n n n Pour que vous compreniez les possibilités de ces techniques. Que vous pouvez adapter à vos problèmes. Que vous pouvez incorporer dans des solutions plus complètes.

5 Motivation n Beaucoup des problèmes en traitement d’image peuvent être exprimés ainsi: n n n Trouver une structure linéique avec telles ou telles propriétés. Trouver une région ou son contour (i. e. bord) avec telles ou telles propriétés. Exemples: n n Extraction de réseaux routiers. Extraction de zones urbaines.

6 Exemples

7 Motivation n n Les graphes image sont une représentation discrète de la géométrie de l’image. Les problèmes précédents se traduisent par des problèmes sur des graphes définis à partir de l’image: n n Trouver un chemin (de poids minimum) dans un graphe. Trouver un cycle (de poids (ratio) minimum) dans un graphe.

8 Plan du cours n n n Graphes et graphes image Fonctions sur les graphes Problèmes graphiques et algorithmes n n n Chemins de poids minimum Cycles divers Cycle de poids rationnel minimum Fonctions sur les graphes image Problèmes image Exemples

Graphes et graphes image

10 Graphes orientés: intuition n On peut imaginer un graphe orienté en termes de sommets (cercles verts) et d’arcs (flèches noires): n n n 5 1 On peut avoir des sommets a f isolés (7). On peut avoir des boucles c (g). 4 On peut avoir plus d’un e arc entre deux sommets (h, i). h b 2 d 3 i 6 7 g

11 Graphes orientés n n Un graphe consiste de deux ensembles E (arcs) et V (sommets) et deux applications s (source) et b (but) de E à V: On peut penser à une seule application de E à V £ V: s(e) e b(e) 1 a 4 2 b 1 4 c 2 3 d 2 3 e 4 3 f 1 6 g 6 h 5

12 Types de graphes n Si il y a plus d’un arc entre deux sommets, on a un multigraphe (s £ b pas injective). n n Sinon (s £ b est injective), on peut identifier E avec un sous-ensemble de V £ V. Si il n’y a pas de boucle, on a un graphe simple. Si on a tous les arcs possibles (E = V £ V), le graphe est complet (s £ b surjective). Nous utiliserons le mot graphe pour les nonmultigraphes simples.

13 Graphe symétrique n Pour chaque arc e, il y a un autre arc (e-1) entre les mêmes sommets mais avec l’orientation inverse. n 8 e 2 E. 9 ! e-1 2 E t. q. s £ b(e-1) = b £ s(e).

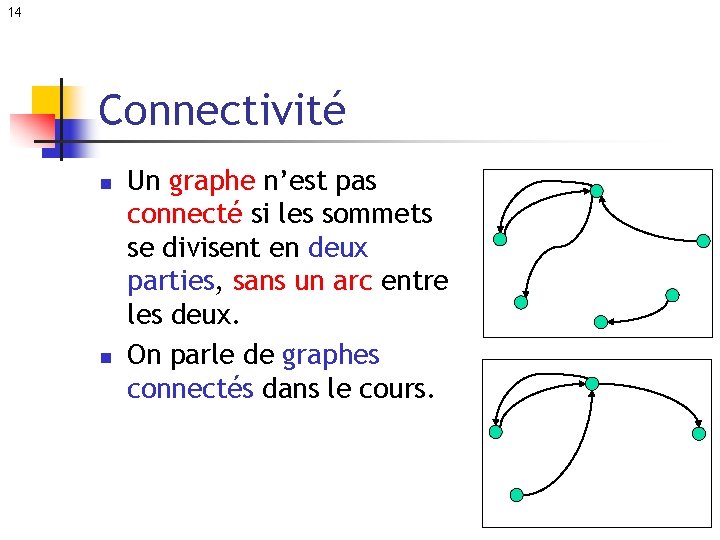
14 Connectivité n n Un graphe n’est pas connecté si les sommets se divisent en deux parties, sans un arc entre les deux. On parle de graphes connectés dans le cours.

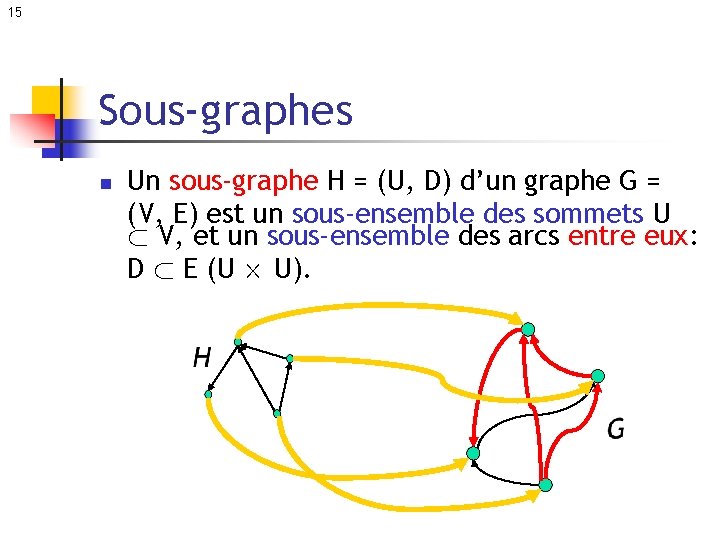
15 Sous-graphes n Un sous-graphe H = (U, D) d’un graphe G = (V, E) est un sous-ensemble des sommets U ½ V, et un sous-ensemble des arcs entre eux: D ½ E (U £ U).

16 Graphes spéciaux: chemins et cycles n Un chemin est une séquence d’arcs: n n {ei}i 2 [1. . n], t. q. b(ei) = s(ei + 1) pour i 2 [1. . (n – 1)]. Un cycle est un chemin avec b(en) = s(e 1). On dit qu’un graphe contient un chemin ou un cycle si il a un sous-graphe qui est un chemin ou un cycle.

17 Simplicité n Graphe acyclique (GA): n n Chemin simple: n n Une graphe qui ne contient pas un sous-graphe qui est un cycle. Une chemin qui ne contient pas un sous-graphe qui est un cycle. Cycle simple: n Un cycle qui ne contient pas un sous-graphe propre qui est un cycle.

18 Graphes image n n V est l’ensemble des pixels. Deux graphes symétriques: n n n Vert: G = (E, V). Rouge: G = (E, V). Il existe une bijection ¤: E $ E. n n Rotation positive de p/2. ¤¤e = e-1. =

19 Exemples Image =

20 Et maintenant? n On cherche un chemin ou un cycle dans un des deux graphes image. n n On définit une fonction (poids) qui donne une valeur pour chaque chemin ou chaque cycle dans le graphe. n n Mais comment on va le sélectionner? On cherche le chemin ou le cycle avec le poids minimum. Comment construire une telle fonction?

Fonctions sur les graphes

22 Fonctions sommet et arc n Sommets: n n Arcs: n n Pour chaque sommet v, on a une valeur (un poids) f(v). Pour chaque arc e, on a une valeur (un poids) f(e). On peut définir la dérivée d’une fonction sommet, qui est un fonction arc: n (df)(e) = f(b(e)) – f(s(e)).

23 Fonctions spéciales n On peut définir des fonctions n n Positives: f(u) > 0. Entières: f(u) 2 Z. Binaires: f(u) 2 {0, 1}. (Sous-ensemble de U. ) Soit g et h deux fonctions, h positive. n On définit une fonction rationelle g/h(u) = g(u)/h(u).

24 Fonctions symétriques n n Rappel qu’un graphe symétrique a pour chaque arc e, un arc e-1. Pour les fonctions arc, on définit: n n On définit les fonctions symétriques: n n -1(e) = (e-1). = -1 On définit les fonctions antisymétriques: n = - -1 (e) = 2 (e-1) = § 2

25 Fonctions sur ensembles n Etant donné une fonction sommet ou arc, on peut définir une fonction sur sous-ensembles de V ou E par sommation. E. g. : n n n U ½ V; f(U) = v 2 U f(v). Noter que df(c) = 0 si c est un cycle.

26 Cycles négatifs n n Une fonction arc a un cycle négatif si le graphe contient un cycle c t. q. (c) < 0. Les cycles négatifs jouent une rôle important dans la suite du cours.

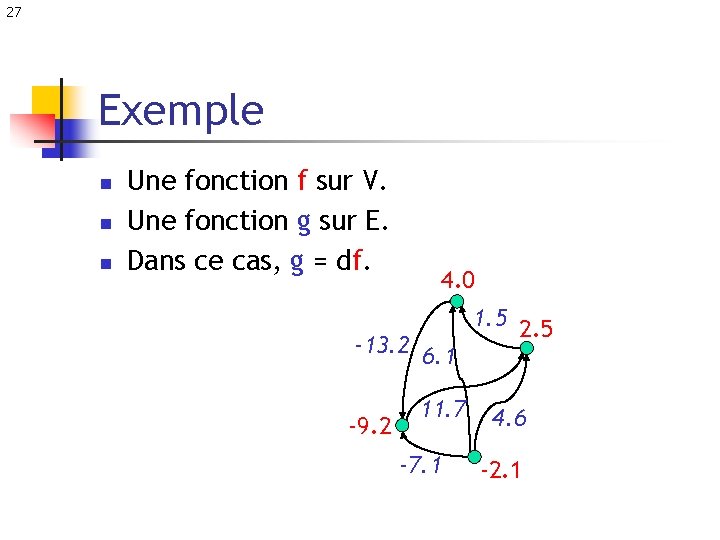
27 Exemple n n n Une fonction f sur V. Une fonction g sur E. Dans ce cas, g = df. 4. 0 -13. 2 6. 1 -9. 2 11. 7 -7. 1 1. 5 2. 5 4. 6 -2. 1

28 Et maintenant? n n On a vu comment définir des fonctions sur les chemins et les cycles. Comment trouver le chemin ou cycle avec le poids minimum?

Problèmes graphiques et algorithmes

30 Problèmes n n Chemins de poids minimum. Cycle de poids minimum. Détection de cycles négatifs. Cycle de poids rationel minimum.

31 Généralités n On suppose: n Un graphe G = (E, V). n n C est le sous-ensemble de cycles dans G. Deux fonctions arc, et . n n est positive. n’est pas toujours utilisé. On peut supposer que et sont entiers.

Problèmes graphiques et algorithmes I Chemins de poids minimum

33 Chemins de poids minimum n Problème: n n Trouver le chemin qui a le poids minimum de parmi les chemins qui passent entre un sommet s et un sommet t. Différents Cas: n n G contient un cycle négatif. G ne contient aucun cycle négatif.

34 Différents cas Chemin simple Cycle négatif Pas de cycle négatif ¸ 0 : impossible. GA. ¸ 0. général. Mal défini général. NP-complet ¸ 0 : impossible. général. GA. ¸ 0. général. Par défaut, on trouve un chemin simple.

35 Notations, Init et Relax n A la fin de chaque algorithme: n n d: V ! R sera le poids du chemin de poids minimum (valeur minimal de ) entre s et v. r: V ! V est le prédécesseur de chaque sommet dans le chemin de poids minimum de s. n Init(d, s) n n d(s) = 0; 8 v 2 Vn{s}: d(v) = 1; Relax(e, d, r, ) n Si d(b(e)) > d(s(e)) + (e) n n d(b(e)) = d(s(e)) + (e) r(b(e)) = s(e)

36 ¸ 0: algorithme de Dijkstra n Dijkstra(G, s, ) n n n Init(d, s) Q=V Tant que Q ¹ ; n n n u = arg minv 2 Q {d(v)} Q = Qn{u} Pour e 2 s-1(u) n n Relax(e, d, r, ) Complexité: O(E log(V)).

37 général: algorithme de Bellman/Ford n Bellman. Ford(G, s, ) n n Init(d, s) Pour n 2 {1, …, (j. Vj – 1)} n n Q=V Tant que Q ¹ ; n n n u = arb(Q); Q = Qn{u} Pour e 2 s-1(u) n n Relax(e, d, r, ) Complexité: O(VE).

38 Commentaire n Noter que si l’on veut calculer la distance entre un sommet et un sous-ensemble des autres sommets l’algorithme de Dijkstra peut être arrêté au point où les sommets sont selectionnés.

Problèmes graphiques et algorithmes II Cycles divers

40 Cycle de poids minimum Cycle négatif Cycle Pas de cycle négatif ¸ 0 : impossible. ¸ 0. Trivial. général. Mal défini général. d = - dd ¸ 0. Cycle général. simple NP-complet Trivial. ¸ 0 : impossible. général. d = - dd Par défaut, on trouve un cycle simple, mais trivial.

41 Détection de cycles: algorithme n Cycle(G) n Pour v 2 V n Si M(v) = 0 n n DFS (v) DFS(v) – depth-first search – recherche par profondeur d’abord n n M(v) = 1; Pour u 2 b(s-1(v)) n Si M(u) = 0 n n n Si M(u) = 1 n n n r(u) = v DFS(u) r(u) = v Rend u (cycle détecté) M(v) = 2

42 Détection de cycles négatifs: algorithme n Cyc. Neg(G, ) n n n s = arb(V) d = Bellman. Ford(G, s) Pour e 2 E n n n u = s(e) v = b(e) Si d(v) > d(u) + (e) (ou dd(e) > (e)) n Il y a une cycle négatif.

43 Détection de cycles zéro. n d(v) · d(u) + (hu, vi). Donc d(hu, vi) = (hu, vi) - dd(hu, vi) est n positive. Pour un cycle c: n n n d(c) = (c) parce que df(c) = 0 pour toutes fonctions sommet f et tous cycles. Donc, (c) = 0 ) d(e) = 0 8 e 2 c.

44 Cycles zéro: algorithme n Zero. Cyc(G, ) n n n s = arb(V) d = Bellman. Ford(G, s, ) E 0 = {e 2 E : d(e) = 0} G 0 = (E 0, b(E 0) [ s(E 0)) c = Cycle(G 0)

Problèmes graphiques et algorithmes III Cycle de poids rationnel minimum

46 Cycle de poids rationnel minimum n Problème: n n n Trouver arg minc 2 C / (c). Ce problème ne presente pas les difficultés rencontrées avec le cycle de poids minimum. Dans les applications, il y a aussi des propriétés théoriques intéressantes.

47 Cycle de poids rationnel minimum Cycle négatif Cycle ¸ 0 : impossible. général Par défaut, on trouve Cycle général un cycle simple. ¸ 0 : impossible. Pas de cycle négatif ¸ 0. G, sym: trivial. général. d = - dd Par défaut, on trouve un cycle simple.

48 Commentaires n Pas de restriction sur : n n n peut avoir des cycles négatifs. On trouve toujours un cycle simple. Pour les graphes symétriques, antisymétrique, symétrique: n n arg minc 2 C / (c) = arg maxc 2 C j / (c)j. Donc l’algorithme maximise j / j.

49 Lemmes n n On définit une fonction arc paramétrisée b = - b. Lemme: Soit b¤ t. q. minc 2 C b¤(c) = 0 et soit c¤ un cycle minimisant b¤(c¤) = 0, alors b¤ = minc 2 C / (c) et / (c¤) = b¤. n n n b(c) = 0 ) / (c) = b. Supposons b¤ ¹ minc 2 C / (c), alors 9 c t. q. / (c) < b¤ ) b¤(c) < 0. Contradiction parce que minc 2 C b¤(c) = 0. Lemme: Soit b¤ = minc 2 C / (c) et soit c¤ un cycle minimisant, alors minc 2 C b¤(c) = 0 et b¤(c¤) = 0. n n b(c) = 0 ( / (c) = b. Supposons minc 2 C b¤(c) ¹ 0, alors 9 c t. q. b¤(c) < 0 ) / (c) < b¤. Contradiction parce que b¤ = minc 2 C / (c).

50 Nouveau problème n n Donc le problème devient: comment trouver b¤ t. q. minc 2 C b¤(c) = 0, puis comment trouver un cycle de poids zéro. Noter: n n min = mine 2 E (e) · b¤ · maxe 2 E (e) = max 9 c 2 C. b(c) < 0 ) minc 2 C b(c) < 0 ) b > b¤ b(c) < 0 ) b¤ · / (c) < b / (c) ¹ / (c 0) ) j / (c) - / (c 0) j ¸ (E max)-2

51 Cycle de poids rationnel minimum: algorithme n Cycle. PRM(G, , ) n n b = maxe 2 E (e) Tant que c = Cyc. Neg(G, b) n n n b = / (c) b¤ = b c¤ = Zero. Cyc(G, b¤)

52 Et maintenant? n n Etant donné les fonctions arc et , on peut trouver le chemin de poids minimum ou le cycle de poids rationnel minimum. Mais étant donné une image, comment construire ces fonctions? n n Une image est une fonction sur les sommets rouges, l’intensité. Le résultat de l’application d’un filtre (e. g. qui mesure une texture) est une fonction sommet rouge.

Fonctions sur les graphes image

54 Graphes image n Deux graphes symétriques: n n Vert: G = (E, V). Rouge: G = (E, V). V est l’ensemble des pixels. Il existe une bijection ¤: E $ E. n n Rotation positive de p/2. ¤¤e = e-1. =

55 Fonctions simples n Etant donné une fonction f sur les sommets rouges, on peut définir une fonction g sur les arcs rouges: n n g(e) = h(f(s(e)), f(b(e))). Deux exemples: n Somme: h(x, y) = x + y. n n n Fonction symétrique. « L’intégrale » de f le long d’un chemin. Différence: h(x, y) = x – y. n n n h = df. Fonction antisymétrique. Pas très utile: si c est un cycle, alors df(c) = 0.

56 Fonctions duelles n Etant donné une fonction f sur les arcs rouges, on peut definir une fonction ¤f sur les arcs verts (et vice-versa): n n n ¤f(e) = f(¤e). Donc, étant donné une fonction f sur les sommets rouges, on peut définir une fonction ¤df sur les arcs verts. Pour un cycle c: n n ¤df(c) = e 2 c [f(b(¤e)) – f(s(¤e))]. Donc le flux du gradient de f à travers c. Dérivée: elle décrit les changements de f. Propriété de bord.

57 Fonction arc ) fonction sommet n Etant donné une fonction arc vert (rouge) f antisymétrique, définir la dérivée df comme la fonction sommet rouge (vert): n n n df(v) = e 2 c(v) f(e) Où c(v) est le cycle autour de v (choix d’orientation). Théorème de Stokes/Green: n Pour un cycle c: f(c) = v 2 Int(c) df(v).

58 Fonction sommet ) fonction arc n Pour chaque fonction sommet rouge (vert), on peut trouver une fonction arc vert (rouge) antisymétrique Af t. q. n n n d. Af = f Alors, on a v 2 Int(c) f(v) = Af(c). Donc on peut calculer « l’intégrale » de f sur une région, mais en utilisant les arcs. n n Intégrale: elle décrit le masse de f. Propriété de région.

59 Fonctions arc antisymétriques n Trois façons pour créer une fonction arc antisymétrique à partir d’une fonction sommet rouge: n f a df. n n f a df a ¤df. n n n Pas très utile: si c est un cycle, alors df(c) = 0. Dérivée: elle décrit les changements de f. Propriété de bord. f a A f. n n Intégrale sur une région: elle décrit le masse de f. Propriété de région.

60 Fonctions arc symétriques n Trois façons pour créer une fonction arc symétrique: n Directement: n n n À partir d’une fonction sommet rouge, en utilisant une fonction h symétrique. n n 8 e 2 E. (e) = 1. 8 e 2 E. (e) = la longueur géométrique de e = l(e). « L’intégrale » de f le long d’un chemin. À partir de , fonction arc antisymétrique: n n On définit = j j par j j(e) = j( (e))j. Exemple j¤dfj: gradient sans orientation.

Problèmes image

62 Modélisation n n On veut trouver une structure linéique ou une région dans une image qui correspond à un objet. Il faut construire des fonctions arc (rouge ou vert) qui incorpore: n n Notre connaissance a priori des propriétés de l’objet. La relation entre l’objet et l’image.

63 Commentaires n Ces exemples sont illustratifs. Ils ne sont pas les solutions complètes aux problèmes mentionnés. Pourquoi? n Les solutions complètes n’existent pas. n n E. g. l’extraction des réseaux routiers est encore un sujet actuel de recherche (problème ouvert). Il vaut mieux d’expliquer comment on peut appliquer ces techniques que de donner des méthodes toutes faites. n Chaque problème est différent et il faut penser au problème spécifique.

64 Réseaux routiers n Un réseau routier est composé de routes, donc: n n On voudrait une chaîne de pixels: n n Un fonction arc symétrique et positive . Deux types de modélisation: n n n On va utiliser le graphe rouge. On doit définir: n n Utiliser les chemins de poids minimum et l’algorithme de Dijkstra. Géométrie a priori. Attache aux données. On va construire = k G + A, (k 2 R+).

65 Géométrie a priori n La possibilité la plus simple est: n n G = l, la longueur géométrique. Donc, sans A: n Le chemin de poids minimum entre deux sommets est donc le chemin le plus court.

66 Attache aux données n n n Soit f une fonction sommet rouge, l’intensité des pixels. Les chemins sont souvent clairs et ont une radiométrie homogène. Donc, on peut essayer: n A(e) = exp[-a(f(b(e)) + f(s(e))], a 2 R+.

67 Initialisation n n Pour utiliser l’algorithme de Dijkstra, il faut s. On ne veut pas les chemins de s à tous les autres sommets: n n Juste aux sommets qui font partie d’un chemin. Choisir les intersections des routes avec le bord de l’image.

68 Résultat réel

69 Bord d’une région n Le bord d’une région est un cycle: n n On voudrait le bord d’une région: n n On va utiliser le graphe vert. On doit définir: n n n Utiliser le cycle de poids rationel minimum. Un fonction arc antisymétrique . Un fonction arc symétrique et positive . Rappel: l’algorithme essaye de maximiser j / j.

70 Modèle simple 1. n n Soit f une fonction sommet rouge, l’intensité des pixels. Donc = ¤df mesure la somme des valeurs du gradient orienté sur le bord. Soit = l, la longueur géométrique. / mesure la densité du gradient sur le bord. n n L’algorithme va la maximiser. Point positif: invariant à l’échelle. n n Par contre, dépend de la longueur du bord. Point négatif: les bords qui ont un gradient qui s’inverse.

71 Modèle simple 2 n n n Soit f une fonction sommet rouge ´ 1. = Af mesure l’aire de la région. Soit g une fonction sommet rouge, l’intensité des pixels. = 1/j¤dgjmesure la somme des valeurs inverses du gradient non-orienté sur le bord. Donc, j / j est grand quand: n n L’aire est grande. Les gradients sont identiques et grands.

72 Resultat synthétique (1) 1. 2. 3. (2) (3) Un bord pour lequel le gradient s’inverse. Résultat avec modèle 1. Résultat avec modèle 2.

73 Résultat réel Cratère Lunaire: JPL

Fin

75 GA: ordre topologique n n On peut définir un ordre Á des sommets t. q. si u Á v, il n’existe aucun chemin de v à u. OT(G) n On a: n Pour v 2 V n Si M(v) = 0 n n OTT(v, T) n n n M(v) = 1; T = T + 1; Pour u 2 b(s-1(v)) n Si M(u) = 0 n n M: V! {0, 1}. n F: V! Z+ L’ordre est: u Á v , F(v) < F(u). n OTT(u, T) T=T+1 F(v) = T n n L’ordre n’est pas unique. Complexité: O(E).

76 GA: algorithme n CPMGA(G, s, ) n n n Init(d, s) Q=V Tant que Q ¹ ; n n n u = minÁ Q; Q = Qn {u} Pour e 2 s-1(u) n n Relax(e, d, r, ) Complexité: O(E).