Mthodes de Changement dchelle Inclusions Homognisation des Milieux

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Partie 4 A: Problèmes d ’inclusions - Opérateurs de Green • 1 - Inclusion en milieu infini • 1. 1 problème homogène, • 1. 2 problème inhomogène et tenseur d'influence de Hill, • 1. 3 problème inhomogène avec chargement à l'infini, • 1. 4 estimation aux faibles concentrations. • 2 - Opérateur de Green • 2. 1 solution élémentaire en milieu infini, • 2. 2 opérateur de Green modifié, • 3 - Bilan ______________________________________________________________________________________ S. DRAPIER 107

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Motivations Solution pour une inclusion dans un milieu • Inclusion - Eshelby • Opérateur de Green • Tenseur de localisation Homogénéisation des milieux à distribution aléatoires estimations d’ordre 1 et 2 Idée : connaître la solution pour une inclusion dans un milieu de nature différente connaître la solution d’une inclusion, possédant des déformations initiales, constituée du même matériau que le milieu ______________________________________________________________________________________ S. DRAPIER 108

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 1. Inclusion dans un milieu 1. 1 Problème de l’inclusion homogène - Eshelby Utilisation des déformations libres - scénario d ’Eshelby • Rappel : déformation libre = déformation d’un milieu sans générer de contraintes, si le milieu est libre de changer de morphologie • dilatation volumique résultant d’une élévation de température • déformations résiduelles, plasticité, . . . • Inclusion : x 1 2 déformation libre dans l’inclusion et(x I) 3 I V (domaine) et déformation totale dans l’inclusion (mesurable) Totale Compatible Libre ______________________________________________________________________________________ S. DRAPIER 109

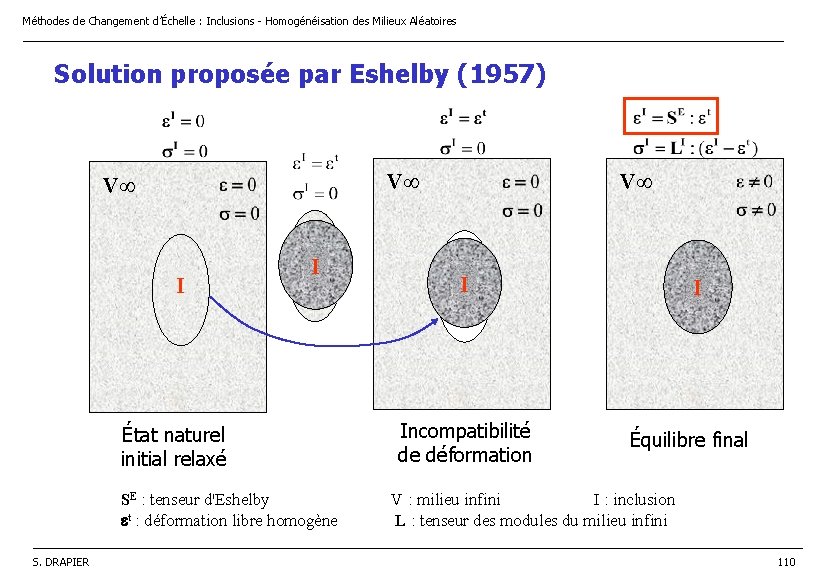
Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Solution proposée par Eshelby (1957) V V I I État naturel initial relaxé SE : tenseur d'Eshelby et : déformation libre homogène V I Incompatibilité de déformation I Équilibre final V : milieu infini I : inclusion L : tenseur des modules du milieu infini ______________________________________________________________________________________ S. DRAPIER 110

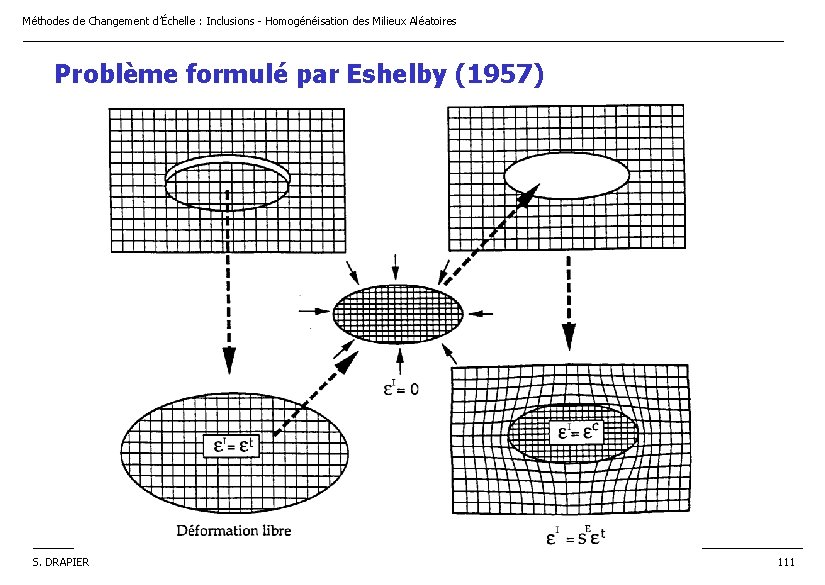
Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Problème formulé par Eshelby (1957) ______________________________________________________________________________________ S. DRAPIER 111

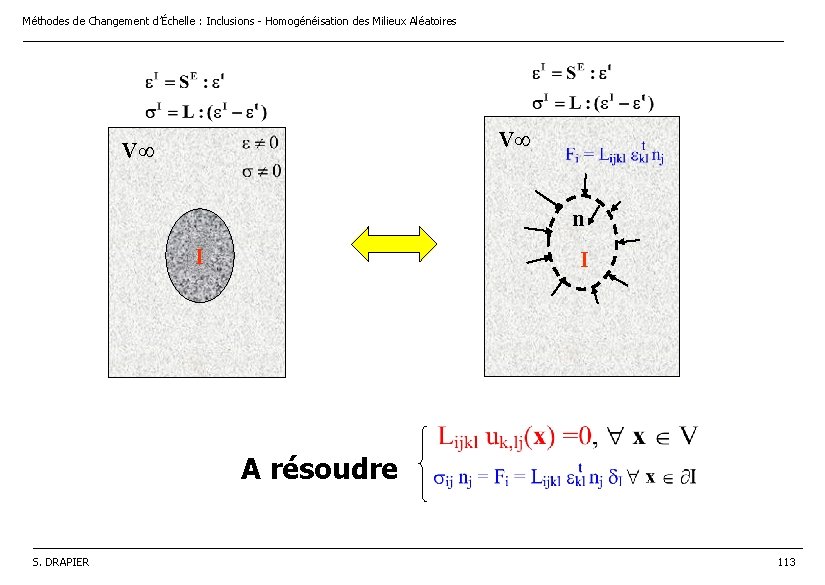
Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Problème homogène L’inclusion I a les mêmes propriétés que le milieu V qui l’entoure e. I • Les déformations doivent être compatibles • d’où l’expression des contraintes (en utilisant la symétrie de L) : • et l’équilibre statique : Efforts qu’il faut imposer sur la frontière de l‘inclusion pour la ramener à une forme compatible ______________________________________________________________________________________ S. DRAPIER 112

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ V V n I I A résoudre ______________________________________________________________________________________ S. DRAPIER 113

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Résolution : fonction de Green en élasticité linéaire u(x) x x' 1 2 3 f(x’) Fonction de Green : gij(x-x') permet d ’exprimer le déplacement u(x) dans la direction xi résultant de l’application d'une force unitaire f en x' dans la direction xj V Eshelby On montre pour Eshelby : pour un milieu non contraint Cadre mathématique au § 2. 1 ______________________________________________________________________________________ S. DRAPIER 114

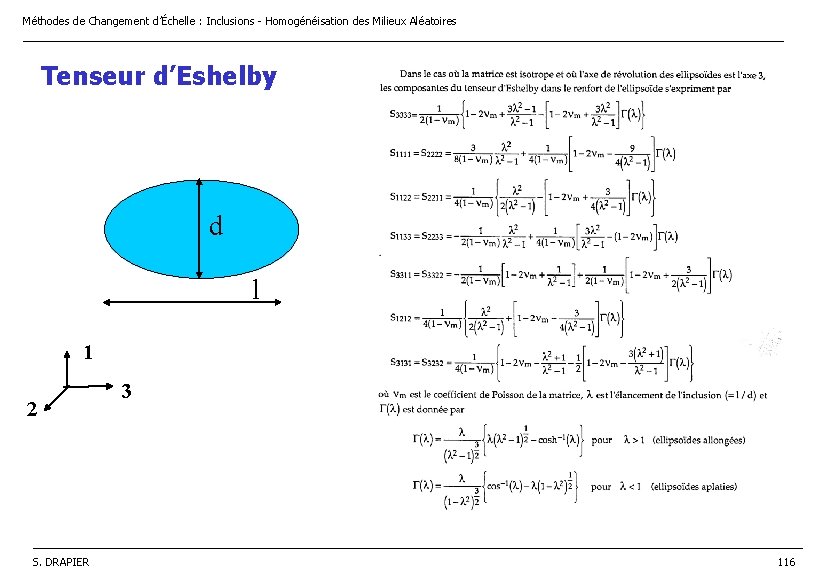
Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Propriétés du tenseur d’Eshelby : • tenseur du 4 ieme ordre • partiellement symétrique mais • expressions analytiques dans les cas simples : ellipsoïde isotrope, déformation uniforme dans l’inclusion Dépend uniquement du coefficient de Poisson et des facteurs géométriques de l’inclusion ______________________________________________________________________________________ S. DRAPIER 115

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Tenseur d’Eshelby d l 1 2 3 ______________________________________________________________________________________ S. DRAPIER 116

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Généralisation Pour généraliser la démarche précédente, on peut passer par la polarisation • Équation de comportement dans l'inclusion : s. I = L: e. I + t t : tenseur de polarisation (symétrique) tel que t = -L: et Contrainte qui apparaîtrait dans l’inclusion si après la transformation (thermique, …) on bloquait la déformation • Autres tenseurs (Hill, 1965) • Déformation dans l'inclusion : e. I = -P: t • Contrainte dans l'inclusion : s. I = -Q: et (P = SE : L-1 = SE: M) (Q = L - L: P: L) • Propriétés de P (plus intéressantes que SE) symétrique, défini positif ______________________________________________________________________________________ S. DRAPIER 118

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 1. 2 Problème inhomogène et tenseur d'influence de Hill (L*)² Extension de la solution d’Eshelby homogène (ellipsoïdale) • LI=L+DLI V Symétrique non nul, mais pas forcément défini positif I LI L • t : polarisation = contrainte correspondant à et si inclusion seule, i. e. sans matériau VI s = L: e dans VI s. I= L: e. I + t’ dans I, = L: e. I + DLI: e. I + t e C. A. dans V s S. A. dans V t = -LI : et ______________________________________________________________________________________ S. DRAPIER 119

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Hypothèse : champ de polarisation homogène dans l’inclusion déformation constante dans l’inclusion Eshelby e. I = -P : t’ L*=P-1 -L = (SE: M)-1 -L e. I = - [L* + LI ]-1 : t Tenseur d’influence de Hill • L* exprime la réaction du milieu infini sur l'inclusion en réponse à la déformation que celle-ci lui impose, (illustration ci-après) • tenseur symétrique, défini positif, de la dimension des modules d’élasticité • dépend uniquement des modules du milieu et de la géométrie de l’inclusion ______________________________________________________________________________________ S. DRAPIER 120

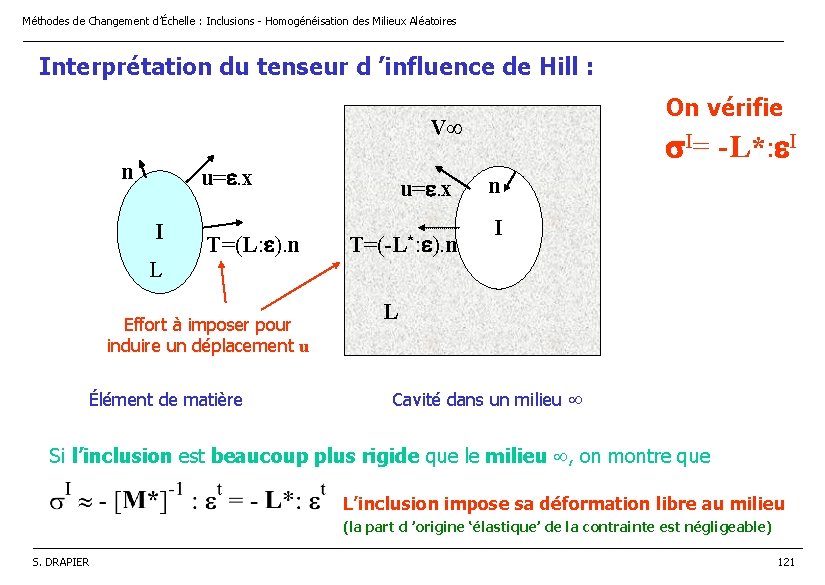
Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Interprétation du tenseur d ’influence de Hill : On vérifie V n u=e. x I T=(L: e). n u=e. x T=(-L*: e). n s. I= -L*: e. I n I L Effort à imposer pour induire un déplacement u Élément de matière L Cavité dans un milieu Si l’inclusion est beaucoup plus rigide que le milieu , on montre que L’inclusion impose sa déformation libre au milieu (la part d ’origine ‘élastique’ de la contrainte est négligeable) ______________________________________________________________________________________ S. DRAPIER 121

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 1. 3 Problème inhomogène avec chargement à l'infini s = L: e dans VI s. I= L: e. I + t’ dans I, avec LI = L+DLI so= L: eo chargement à l'infini e C. A. dans V s S. A. dans V • Élasticité linéaire : superposition des champs macro aux solutions s. I - so=-L*: [e. I - eo] (une seule inclusion inhomogène noyée dans le milieu infini) • Déformation et contraintes homogènes dans l’inclusion : e. I = -P: t’ + eo s. I = - LI: P: t’ + LI eo + so ______________________________________________________________________________________ S. DRAPIER 122

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Remarque : inhomogénéité et Eshelby avec chargement à l ’ La solution précédente s’applique au cas où la déformation est COMPATIBLE (la déformation libre est nulle) s. I - so= -L*: [e. I - eo] dans VI s. I= LI: e. I dans I so= L: eo chargement à l'infini e C. A. dans V s S. A. dans V e. I = [L*+ LI]-1: [L*+L]: eo • Remarques : Localisation • Solution indépendante des propriétés mécaniques de l’inclusion : L*=L: [(SE)-1 -I] ______________________________________________________________________________________ S. DRAPIER 123

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 1. 4 Plusieurs inclusions Eshelby avec 2 inclusions disjointes (centrées en xi) subissant une transformation homogène caractérisée respectivement par t 1 et t 2 V (t 1; t 2) I 1 I 2 e C. A. dans V (dérive d'un champ de dép. ) e 0 loin de (I 1 I 2) s = L: e dans V(I 1 I 2) s. I 1 = LI 1: e + t 1 dans I 1 s. I 2 = LI 2: e + t 2 dans I 2 s S. A. dans V Équations linéaires Superposition : (t 1 = t ; t 2 = 0) + (t 1 = 0; t 2 = t) (t 1; t 2) ______________________________________________________________________________________ S. DRAPIER 124

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ Solution polarisation dans I 1 polarisation dans I 2 Effets des polarisations Dans I 1 par exemple : déformation = déf. homogène induite par t 1 + effet à distance de t 2 (déf. Inhomogène) Généralisation • Généralisation possible avec plusieurs inclusions homogènes • Pas de généralisation possible avec plusieurs inhomogénéités car s = Li : e + ti = L : e + [( Li - L ): e + ti] t’i n’est pas constant dans Ii: e varie ______________________________________________________________________________________ S. DRAPIER 125

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ • Problème inhomogène à une inclusion : Déformation homogène dans Io • Plusieurs inclusions et chargement à l'infini : Déformation non homogène dans Ii ti : polarisation due à l'inclusion Ii xi : centre de l'inclusion Ii gi : tenseur symétrique dépendant de L et de la forme de Ii ______________________________________________________________________________________ S. DRAPIER 126

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 1. 5 Estimation aux faibles concentrations Inclusions distantes les unes des autres : (milieu infini=matrice) • seule la polarisation de l'inclusion sur elle même est considérée déf. macroscopique • milieu = VER, L = Lm , LI = Li Déformation homogène dans une inclusion : ei =[L* m + Li]-1: [L*m+L]: E Cas d'un composite à particules (fraction volumique ci) : contrainte macroscopique : Tenseur des modules effectifs (estimation au 1 er ordre) : LFC = Lm + ci [Li- Lm]: [L*m + Li]-1: [L*m+Lm] Lm : tenseur des modules de la matrice Li : tenseur des modules des inclusions L*m : tenseur d’influence construit à partir des modules de la matrice et des formes des inclusions ______________________________________________________________________________________ S. DRAPIER 127

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 2. Opérateur de Green 2. 1 Solution élémentaire (g) de l ’élasticité en milieu infini Soient x V et so(x) S. A. , avec fo un effort constant appliqué sur le volume dv centré en xo. On a uo(x), eo(x) C. A. , et uo 0, eo 0 loin de xo. Linéarité et invariance des champs par translation donc : $ g tel que uo(x) = g(x-xo). fodv eo(x) = h(x-xo). fodv so(x) = L: h(x-xo). fodv g : opérateur de Green = distribution de tenseurs d'ordre 2 h : champ de tenseur d'ordre 3 ______________________________________________________________________________________ S. DRAPIER 128

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 2. 2 Opérateur de Green modifié, solution d'un problème d'élasticité Soient s(x) S. A. avec f et e(x) C. A. tels que : s(x) = L: e(x) + t(x) PTV avec (u, e) et so : PTV avec (uo, eo) et s : - dérivations h'ijk(x)=hjki(-x) opérateur de Green modifié en déformation Donne le champ de déplacement dû à une polarisation élémentaire tdv en xo ______________________________________________________________________________________ S. DRAPIER 129

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 2. 3 Problème d'inclusions Soit une inclusion I de forme ellipsoïdale dans un domaine V, I centrée à l'origine, t la polarisation homogène dans I alors : Propriétés de G pour tout x¹ 0 : - symétrique - homogène de degré -3 - faible variation loin de l'origine, singularité en 0 • Eshelby - rappel : polarisation t = -L: et En symétrisant / (i, j), (k, l), on retrouve Gijkl ______________________________________________________________________________________ S. DRAPIER 130

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ 3. Bilan 1/ Eshelby inclusion polarisation V • s. I = L: e. I + t I solution e. I = -P: t 2/ Problème inhomogène (LI, L) et tenseur de Hill Tenseur d’influence de Hill L*=P-1 -L = (SE: M) -1 -L s. I= L: e. I +t’ s. I= -L*: e. I 3/ Inhomogénéité et Eshelby avec chargement à l ’ so, eo V s. I - so=-L*: [e. I - eo] Déformation libre nulle LOCALISATION I e. I = [L*+ LI]-1: [L*+L]: eo ______________________________________________________________________________________ S. DRAPIER 131

Méthodes de Changement d’Échelle : Inclusions - Homogénéisation des Milieux Aléatoires ________________________________________________________________ L’essentiel s. I - so=-L*: [e. I - eo] e. I =[L*+ LI]-1: [L*+L]: eo Moyenne sur les VER Estimations courantes • Hashin - Strikman : polarisation homogène/phase • Mori - Tanaka : milieu = matrice • Autocohérent : milieu = composite (définition implicite) ______________________________________________________________________________________ S. DRAPIER 132