Models of Computation Automata and Formal Languages Sam

Models of Computation: Automata and Formal Languages Sam M. Kim

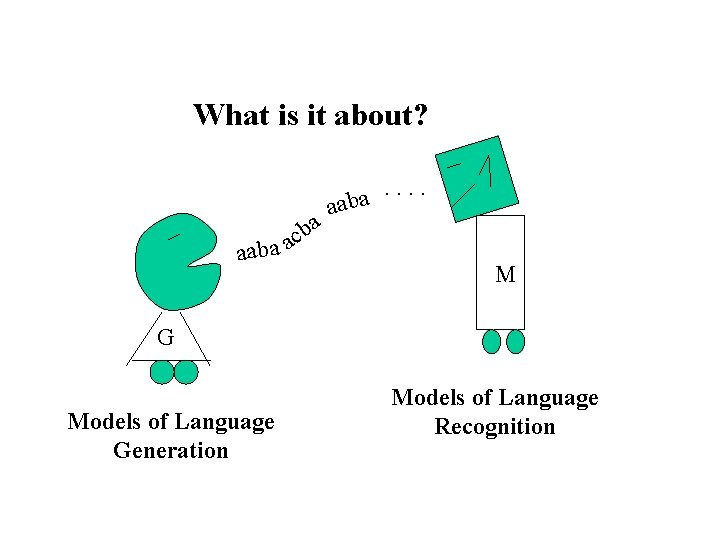
What is it about? a b c aaba a . . a aab M G Models of Language Generation Models of Language Recognition

Where do we use it? almost Everywhere! Everywhere!

Preliminaries Notational Convention • Leading lower case English letters a, b, c, … denote symbols. • Trailing lower case English letters …. . , u, v, w, x, y, z denote strings of symbols. • Upper case English letters, and denote sets. • For a string x, |x| denotes the length of x. • (or ) denotes the null string. • * , which is called Kleene star (or closure) of , denotes the set of all strings over the alphabet including the null string , , and + = * - { }. • xi denotes the repeating string of x i times, and x. R denotes the reverse of string x. For example, (ab)3 = ababab, (ab)0 = , (abcd)R = dcba.

Preliminaries (cont’ed) Set Specification • • Explicit: A = {2, 8}, = {a, b, c} By set properties: A = { x | property list of x} Examples: A = {x | x {a, b}* and x has no consecutive a’s} B = {n | n is an even number} C = {xx. R | x {0, 1}+ } = {00, 11, 0110, 1001, 1111, 001100, . . . } D = {anbncn | n 0} = { , abc, aabbcc, aaabbbccc, . . . }

Proof Techniques • The truth table for implication “if P then Q” (denoted by P Q ) is defined as follows: • P Q T T F F F T T F F T A proposition is a declarative statement that is either true or false. We are interested in proof techniques for propositions of he form P Q, or P Q (i. e. , P Q and Q P ).

Proof Techniques (cont’ed) 1. Trivial proof: Prove, if possible, that Q is true (i. e. , tautology). Notice that if Q is true, then P Q is true independent of P. Example: Suppose that the premise “Graduates of the Computer Science Department get a good job” is true. Then the statement “If the weather is good then the graduates of the Computer Science Department get a good job. ” is true. 2. Vacuous proof: Prove P is false. Notice that if P is false, then P Q is true independent of Q. Example: “If elephants fly, then they will lay eggs. ”

Proof Techniques (cont’d) 3. Indirect proof: Prove that Q P is true. Notice that ( P Q ) (Q P). Example: The proof for “If it rained, then the lawn will be wet. ” is equivalent to the proof for “If the lawn is not wet, then it did not rain. ” 4. Proof by cases: Let P 1, P 2, and P 3 be propositions. Then the proposition (P 1 P 2 P 3) Q can be proved by three cases P 1 Q, P 2 Q, or P 3 Q, because (P 1 P 2 P 3) Q (P 1 Q) (P 2 Q) (P 3 Q) 5. Proof by contradiction: We want to prove that a proposition P is false. With the assumption that P is true, we show that P Q is incorrectly false, contradicting a proven fact. So we must lay the blame on the assumption that P is true.

Proof Techniques (cont’ed) • Dealing with universal/existential quantifications Let P(x 1, x 2, …. , xn), n 1, be a predicate with Boolean variables x 1, x 2, …, xn. For example: GT(x, y) = true if x > y, false otherwise Prime(n) = true if n is a prime number, false otherwise. We will use and to denote “for all (or for every)” and “there exists”, respectively. Symbol is called the universal quantifier, and the existential quantifier.

Proof Technique (cont’ed) 6. Proof by example: To prove that a proposition of the form x [P(x)] (i. e. , there exists an x which satisfies P(x)), it is enough to show an example x which satisfies P(x). However, to disprove the proposition we should present a generalized proof that P(x) is false for arbitrary x, which is not easy. 7. Proof by counter example: To disprove that a proposition of the form x [P(x)] (i. e. , for all x, P(x) is true), it is enough to show an x which does not satisfy P(x). 8. Proof by generalization: To prove a proposition of the form x [P(x)], we need to show that P(x) holds for arbitrary x.

Proof Techniques (cont’ed) 8. Proof by induction: Proof by induction is performed in three steps; (1) base, (2) hypothesis (or assumption), and (3) induction. Example: Prove that n 0 [ (1) Base: when n = 0, 0 i=0 n i=0 i = n(n+1) /2 ] i = 0, and n(n+1)/ 2 = 0. Thus the equality holds. (2) Hypothesis: Suppose that m < n it satisfies (3) Induction step: We prove that for n = m+1, Clearly, n i=0 i = m i=0 i + n, and m i=0 i n m i=0 i = m(m+1) /2. = n(n+1) /2. = m (m+1)/2 by the hypothesis. It follows that m i=0 i + n = m(m+1)/2 + (m+1) = (m+1)(m+2)/2 = n(n+1)/2.

Proof Techniques (cont’ed) • Constructive proof vs non-constructive proof: Constructive proof actually shows the information that the problem requires, while non-constructive proof shows the existence of such information indirectly. Example: We want to prove the statement “There is a prime number p > 2. Constructive proof: 5 is a prime, which is greater than 2. Non-constructive proof: Every natural number can be represented as a product of prime numbers. This fact implies that, if there is no prime number greater than 2, any natural number n should be equal to 2 i for some integer i. However, we know that there exist natural numbers that are not power of 2, which contradicts to a know fact. It follows that there exists a prime number greater than 2.

Proof Technique (cont’ed) Other useful Proof techniques • Pigeonhole Principle: Suppose that we have n pigeonholes and n+1 items to be placed in the pigeonholes. Then however the items placed, at least one pigeonhole will contain at least two items. (This can be easily proved by the proof by induction technique. ) 9. Proof by the pigeonhole principle (example): Show that in a graph G with n vertices, every path of length greater than or equal to n has a cycle. Proof: Let the nodes of G be the pigeonholes and the nodes appearing on the path be the items. We put an item in a mail box (i. e. , a node) if that item appears on the path. If a path length is greater than or equal to n, then it has more than n items. By the pigeonhole principle at least one box will contain at least two items (i. e. , nodes on the path), which implies a cycle on the path.

Proof Techniques (cont’ed) 10. Proof by counting: This technique is used to demonstrate that particular set is larger than others. Example: Prove that, for all n 1, the rows and columns of n n bit matrix do not exhaust all possible binary numbers of length n. Proof. Obviously, there are 2 n different binary numbers of length n, but only 2 n rows and columns in n n bit matrix. Since 2 n < 2 n , for all n > 2, the statement is true for all n > 2. For n = 2 or 1, we can prove by exhaustive argument (this part of the proof is left for the reader).

Proof Techniques (cont’ed) 11. Diagonalization technique: This is a technique that, given a set of n lists, each of length m, construct a list of length m which is not contained in the set. Example: Find a binary number of length n which does not appear on any column or row of an n n bit matrix (recall the preceding example). Solution: Let mii be the complement of the bit at i-th column and i-th row. The matrix does not contain the binary number v = m 11 m 22…mnn. Clearly, i-th row or column has bit mii at its i-th position, while v has mii, the complement at the same position. Hence, there is no n bits number in the matrix that is equal to v.

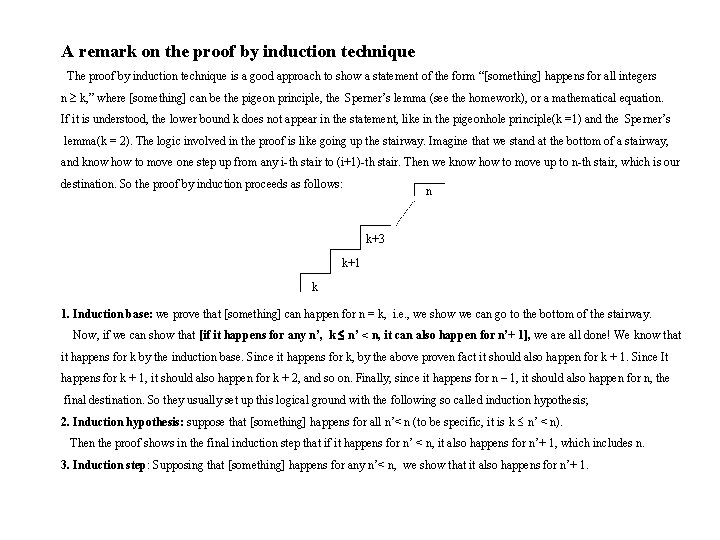
A Rumination on the Proof by Induction • Using the proof by induction technique, prove that the pigeonhole principle is true. Answer: (1) Base: when the number of pigeonholes n = 1, and the number of items m >n. Obviously, the principle is true, because all the items should be in that one pigeonhole. (2) Induction hypothesis: Suppose that the pigeonhole principle is true for any number of pigeonholes n’ < n. (3) Induction step: We show that when the number of pigeonholes is n’+1 and the number of items m > n’+1, the principle also holds. Consider the array of n’+1 pigeonholes as shown below. Case (a): When the last pigeonhole contains no more than one item (i. e. , either zero or one item). The first n’ pigeonholes together contain more than n’ items. By the above induction hypothesis, among the first n’ pigeonholes there exists at least one pigeonhole which contains more than one item. The principle holds. Case (b): When the last pigeonhole contains more than one item. This last pigeonhole witnesses that the principle is true. 1 n’ 2 . . . 1 2 m n’+1

A remark on the proof by induction technique The proof by induction technique is a good approach to show a statement of the form “[something] happens for all integers n k, ” where [something] can be the pigeon principle, the Sperner’s lemma (see the homework), or a mathematical equation. If it is understood, the lower bound k does not appear in the statement, like in the pigeonhole principle(k =1) and the Sperner’s lemma(k = 2). The logic involved in the proof is like going up the stairway. Imagine that we stand at the bottom of a stairway, and know how to move one step up from any i-th stair to (i+1)-th stair. Then we know how to move up to n-th stair, which is our destination. So the proof by induction proceeds as follows: n k+3 k+1 k 1. Induction base: we prove that [something] can happen for n = k, i. e. , we show we can go to the bottom of the stairway. Now, if we can show that [if it happens for any n’, k n’ < n, it can also happen for n’+ 1], we are all done! We know that it happens for k by the induction base. Since it happens for k, by the above proven fact it should also happen for k + 1. Since It happens for k + 1, it should also happen for k + 2, and so on. Finally, since it happens for n – 1, it should also happen for n, the final destination. So they usually set up this logical ground with the following so called induction hypothesis; 2. Induction hypothesis: suppose that [something] happens for all n’< n (to be specific, it is k n’ < n). Then the proof shows in the final induction step that if it happens for n’ < n, it also happens for n’+ 1, which includes n. 3. Induction step: Supposing that [something] happens for any n’< n, we show that it also happens for n’+ 1.

A Rumination on the Proof by Induction Prove that n 0 [ n i=0 i = n(n+1) /2 ] n (3) Induction step: We prove that n’ 2 for n = n’+1, n i=0 i = n(n+1) /2. (2) Hypothesis: Suppose that n’ < n 3 it satisfies m i=0 i = n’(n’+1) /2. 1 0 (1) Base: when n = 0, 0 i=0 i = 0, and n(n+1)/ 2 = 0. Thus the equality holds. 0 + 1 + 2 + . . . . n’(n’+1)/2 + n’ + (n’+1) = (n’+1)(n’+2)/2 = n(n+1)/2

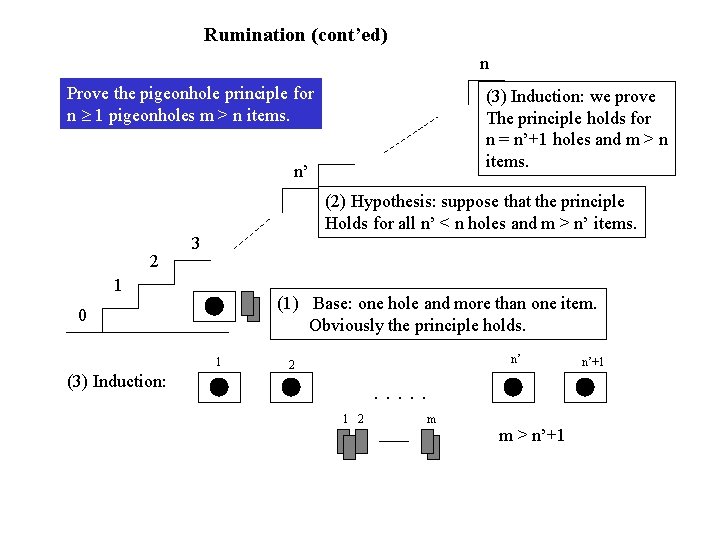
Rumination (cont’ed) n Prove the pigeonhole principle for n 1 pigeonholes m > n items. (3) Induction: we prove The principle holds for n = n’+1 holes and m > n items. n’ (2) Hypothesis: suppose that the principle Holds for all n’ < n holes and m > n’ items. 2 3 1 (1) Base: one hole and more than one item. Obviously the principle holds. 0 1 (3) Induction: n’ 2 . . . 1 2 m m > n’+1