MODELISATION DES LIAISONS MECANIQUES Objectif Lors de ltude

MODELISATION DES LIAISONS MECANIQUES Objectif : Lors de l'étude ou de la conception de la partie opérative d'un système, il est nécessaire de traduire le cahier des charges par un schéma précisant l'agencement et les mouvements des différents composants. Cette modélisation, nécessaire à l'étude mécanique, permettra de choisir les matériaux et de dimensionner les composants de cette partie opérative. Ce schéma faisant apparaître les liaisons entre les différents solides, il est important de connaître parfaitement cette représentation schématique normalisée.

MODELISATION DES LIAISONS MECANIQUES Liaisons : On parle de liaison si et seulement si des surfaces de contact existent. Lorsque deux solides S 1 et S 2 sont en contact, on dit qu'il existe une liaison, notée LS 1/S 2 entre ces deux solides. L'analyse d'une liaison se fait uniquement entre deux solides S 1 et S 2 (ou entre deux classes d'équivalence) sans tenir compte du reste de l’environnement. On définit alors le solide (ou classe d’équivalence) de référence, noté ici S 1 et on étudie la mobilité de l'autre solide, noté ici S 2, par rapport au solide de référence. S 2 S 1

MODELISATION DES LIAISONS MECANIQUES Caractéristiques géométriques des contacts : Les deux solides en contact sont supposés indéformables. Contact ponctuel Contact linéaire Contact surfacique

MODELISATION DES LIAISONS MECANIQUES Décomposition du déplacement d'un solide dans un repère

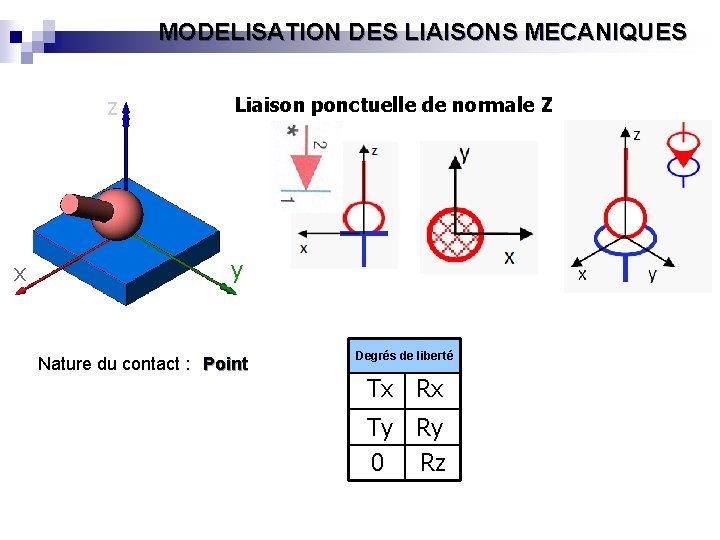
MODELISATION DES LIAISONS MECANIQUES z Liaison ponctuelle de normale Z Z X x x y Nature du contact : Point z Y x Degrés de liberté Tx Rx Ty Ry 0 Rz y

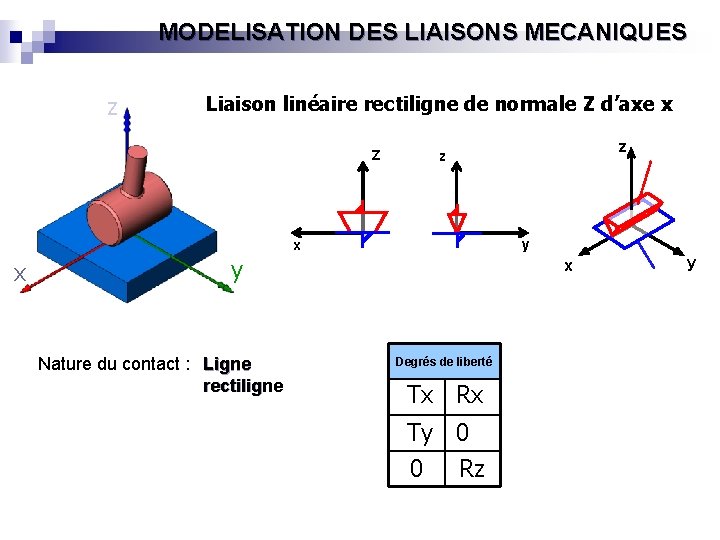
MODELISATION DES LIAISONS MECANIQUES z Liaison linéaire rectiligne de normale Z d’axe x Z y x x y Nature du contact : Ligne rectiligne z z x Degrés de liberté Tx Rx Ty 0 0 Rz y

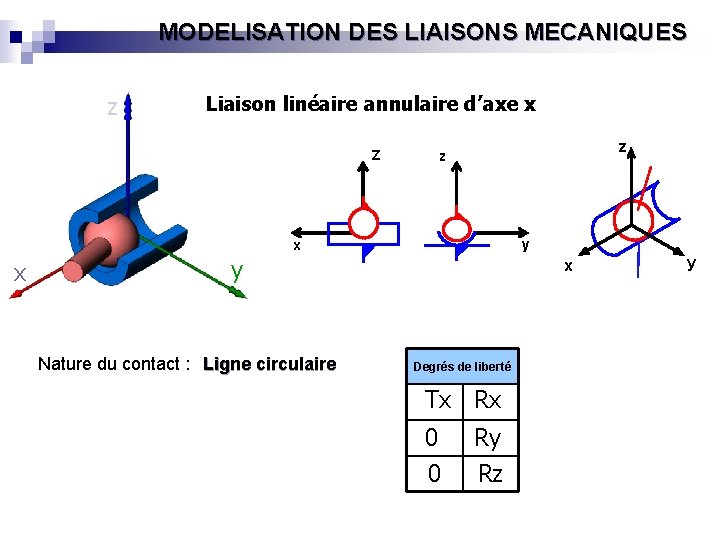
MODELISATION DES LIAISONS MECANIQUES z Liaison linéaire annulaire d’axe x Z z z y x x y Nature du contact : Ligne circulaire x Degrés de liberté Tx Rx 0 0 Ry Rz y

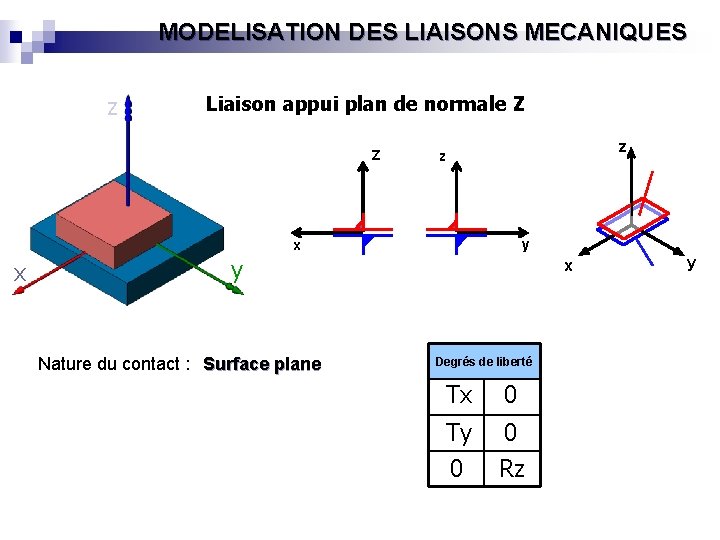
MODELISATION DES LIAISONS MECANIQUES z Liaison appui plan de normale Z Z z z y x x y Nature du contact : Surface plane x Degrés de liberté Tx 0 Ty 0 0 Rz y

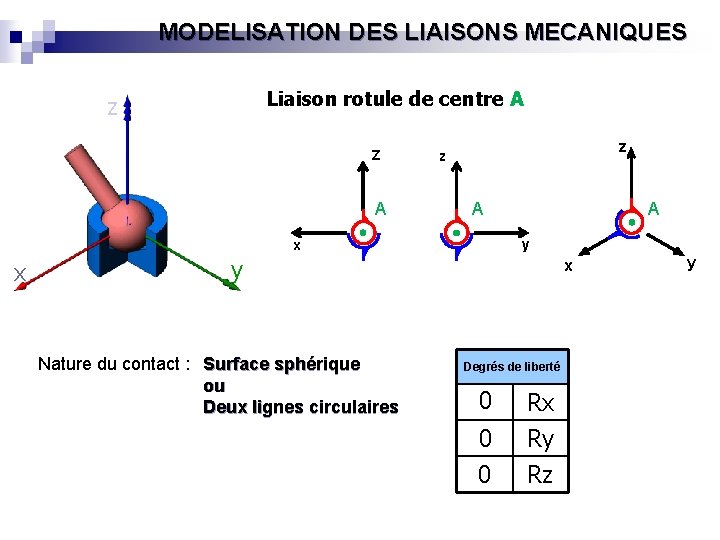
MODELISATION DES LIAISONS MECANIQUES Liaison rotule de centre A z Z A z z A y x x A y Nature du contact : Surface sphérique ou Deux lignes circulaires x Degrés de liberté 0 Rx 0 0 Ry Rz y

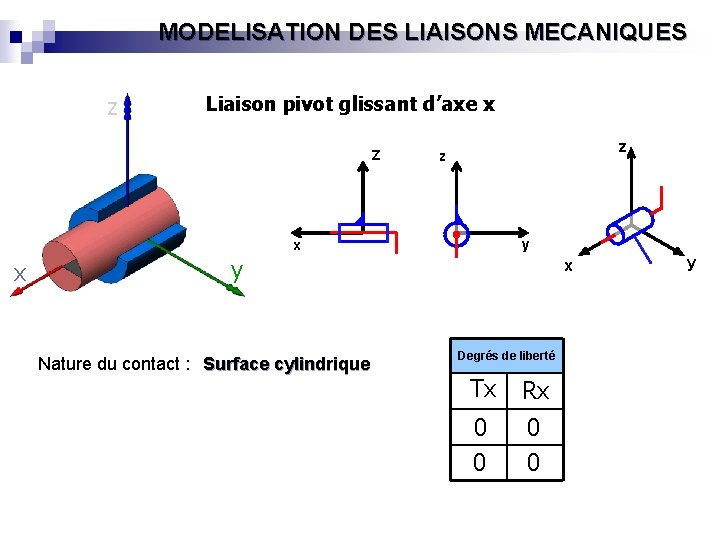
MODELISATION DES LIAISONS MECANIQUES z Liaison pivot glissant d’axe x Z z z y x x y Nature du contact : Surface cylindrique x Degrés de liberté Tx Rx 0 0 y

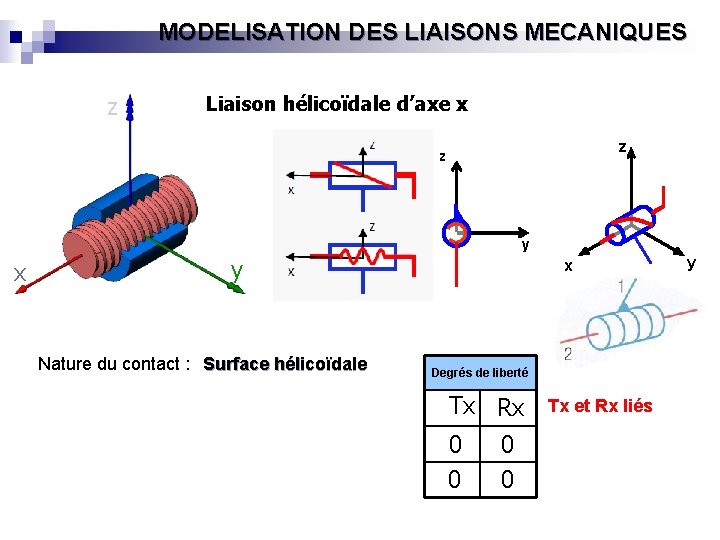
MODELISATION DES LIAISONS MECANIQUES z Liaison hélicoïdale d’axe x Z z z y x x y Nature du contact : Surface hélicoïdale x Degrés de liberté Tx Rx 0 0 Tx et Rx liés y

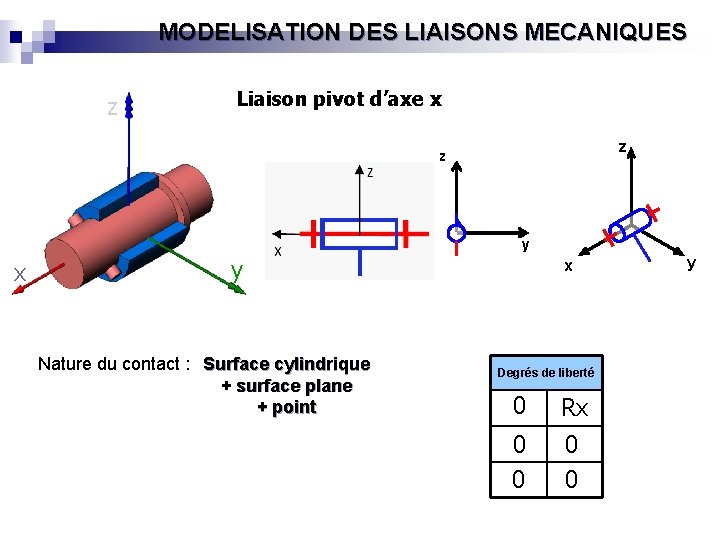
MODELISATION DES LIAISONS MECANIQUES z Liaison pivot d’axe x Z x y x Nature du contact : Surface cylindrique + surface plane + point z z y x Degrés de liberté 0 Rx 0 0 y

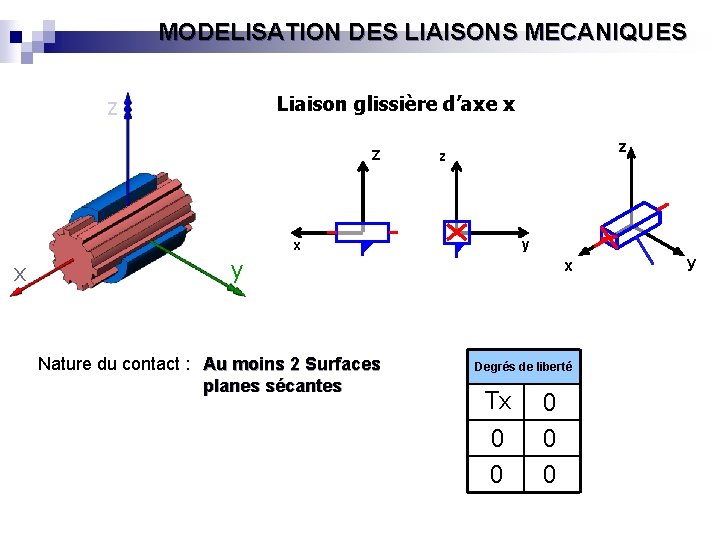
MODELISATION DES LIAISONS MECANIQUES Liaison glissière d’axe x z Z z z y x x y Nature du contact : Au moins 2 Surfaces planes sécantes x Degrés de liberté Tx 0 0 0 y

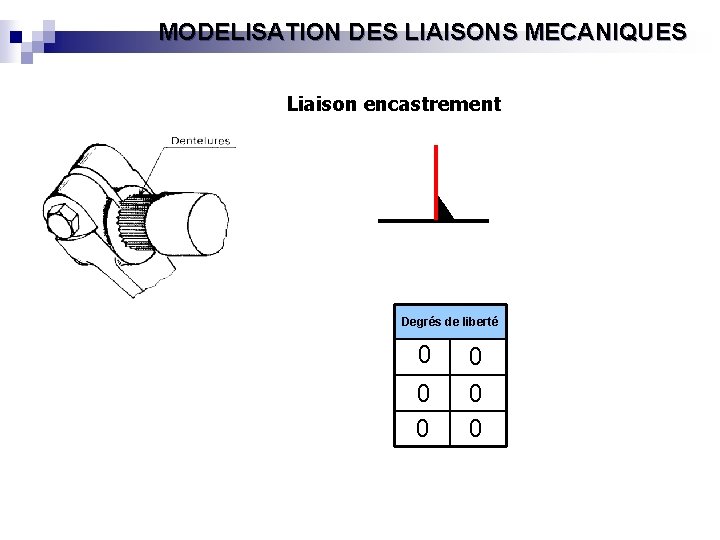
MODELISATION DES LIAISONS MECANIQUES Liaison encastrement Degrés de liberté 0 0 0

MODELISATION DES LIAISONS MECANIQUES Notion de modélisation des mécanisme. Un mécanisme est un ensemble de pièces mécaniques reliées entre elles par des liaisons. Cet ensemble est conçu pour réaliser une ou plusieurs fonctions.

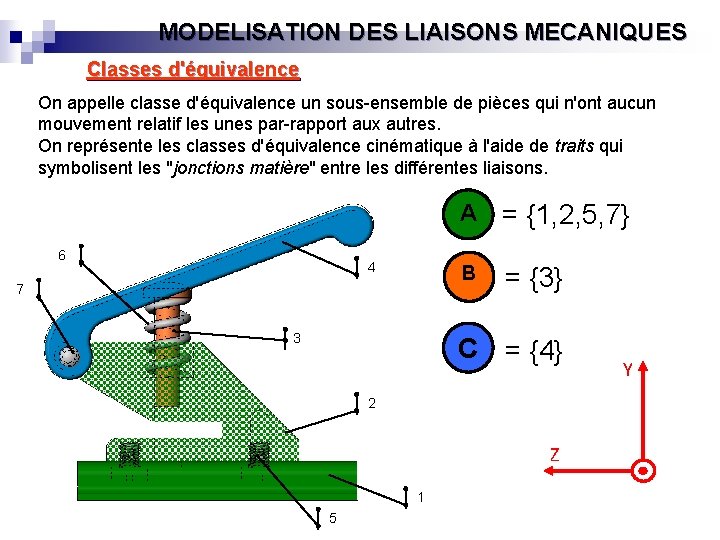
MODELISATION DES LIAISONS MECANIQUES Classes d'équivalence On appelle classe d'équivalence un sous-ensemble de pièces qui n'ont aucun mouvement relatif les unes par-rapport aux autres. On représente les classes d'équivalence cinématique à l'aide de traits qui symbolisent les "jonctions matière" entre les différentes liaisons. 6 4 7 3 A = {1, 2, 5, 7} B = {3} C = {4} 2 Z 1 5 Y

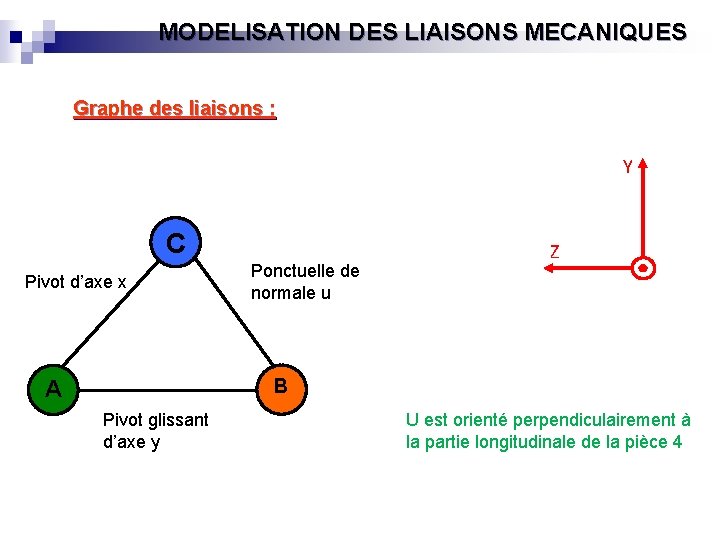
MODELISATION DES LIAISONS MECANIQUES Graphe des liaisons : Y C Pivot d’axe x Ponctuelle de normale u Z B A Pivot glissant d’axe y U est orienté perpendiculairement à la partie longitudinale de la pièce 4

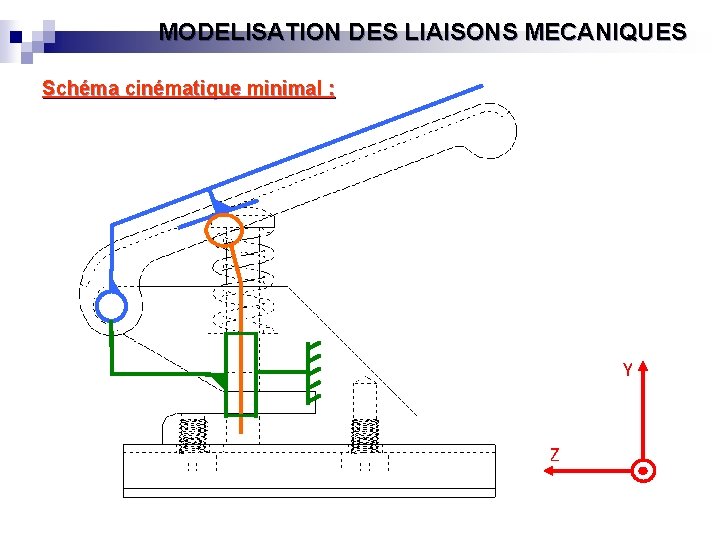
MODELISATION DES LIAISONS MECANIQUES Schéma cinématique minimal : Y Z