Method of sections Method of Sections It is








- Slides: 25

Method of sections

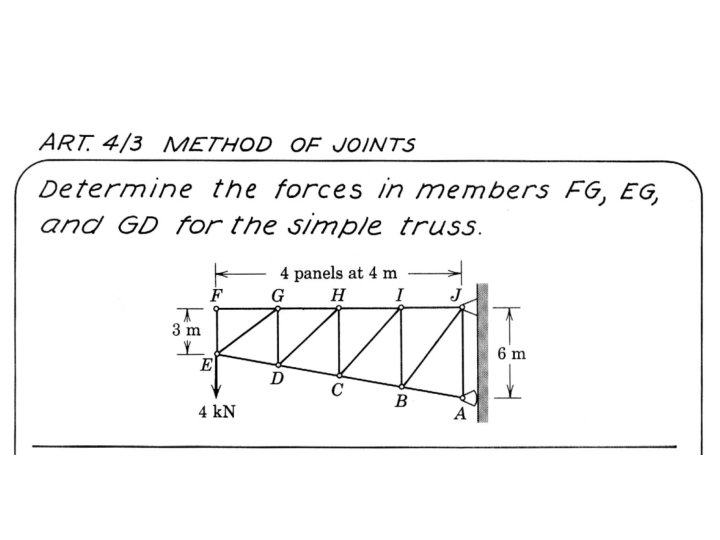
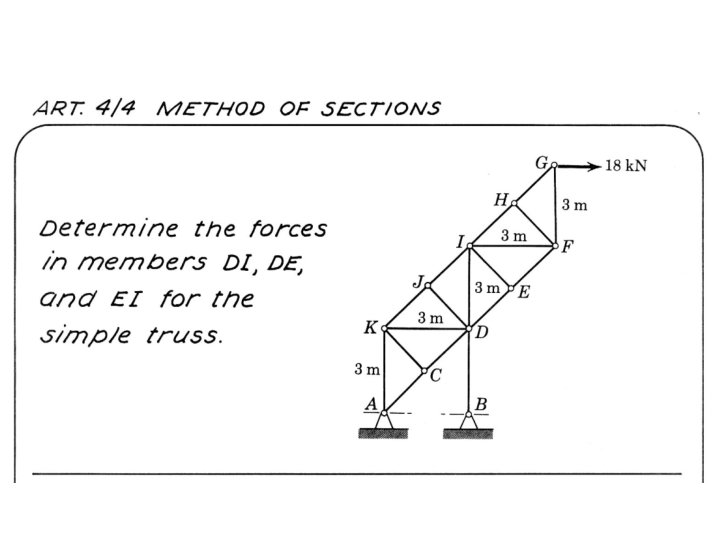
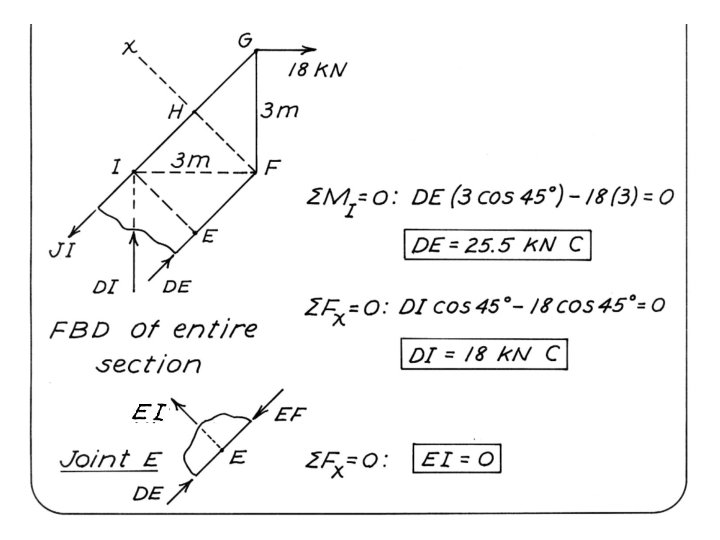
Method of Sections • It is based on the principle that if the truss is in equilibrium then any segment of the truss is also in equilibrium. • In this method, a section is passed through the truss to cut it into two parts so that internal forces are exposed at the cut members. • Equations of equilibrium are then applied to the free body diagram of either of the two parts to determine the desired forces. • In choosing a section of the truss, in general, not more than three members whose forces are unknown may be cut, since there are only three available equilibrium equations which are independent. • The method of sections has the basic advantage that the force in almost any desired member may be found directly. March 6, 2021 2

An Important Note If a body is in equilibrium under the action of external forces (including support reactions) then its each and every part is also in equilibrium under the action of external and internal forces. 3/6/2021 3

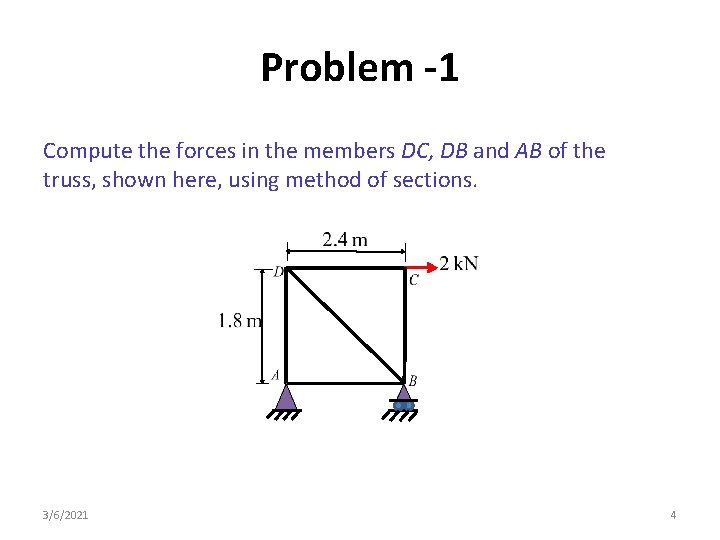
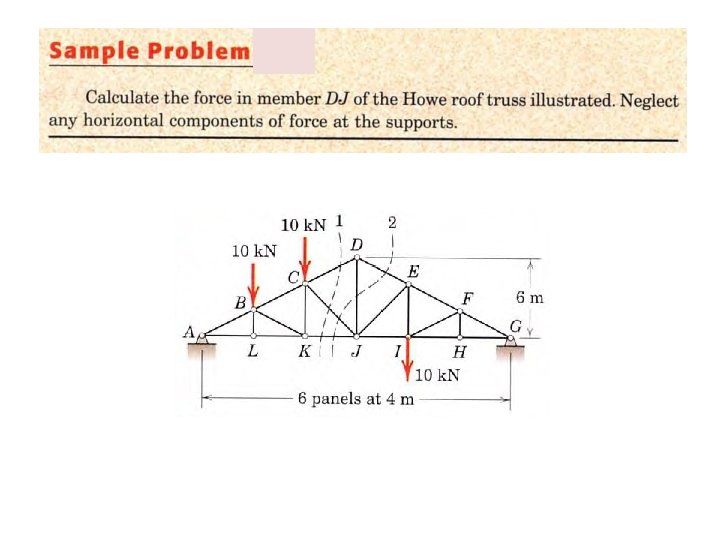
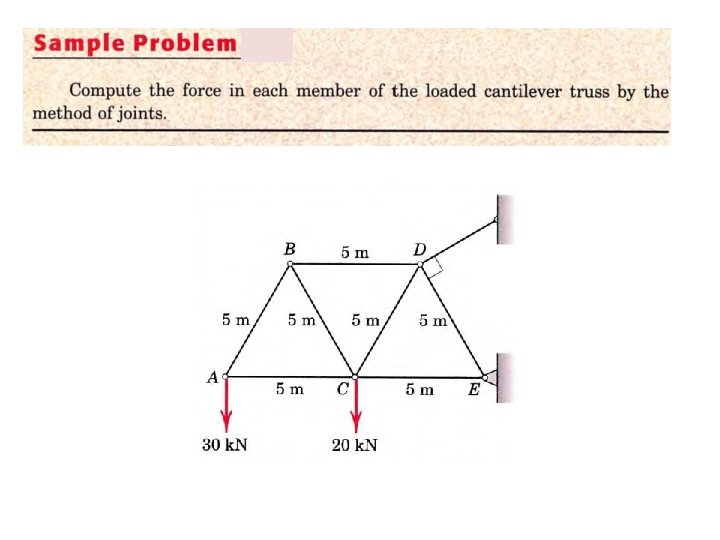
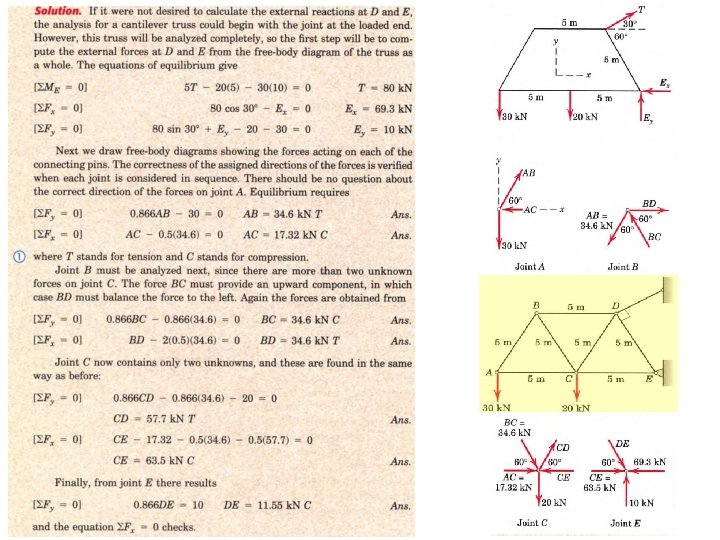
Problem -1 Compute the forces in the members DC, DB and AB of the truss, shown here, using method of sections. 3/6/2021 4

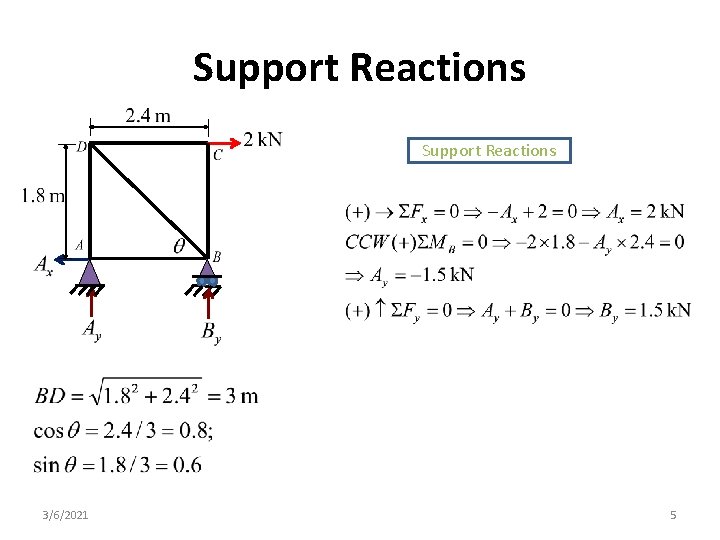
Support Reactions 3/6/2021 5

Calculation of the member forces For convenience, assume tension in all the cut members. 3/6/2021 6

Calculation of the member forces 3/6/2021 7

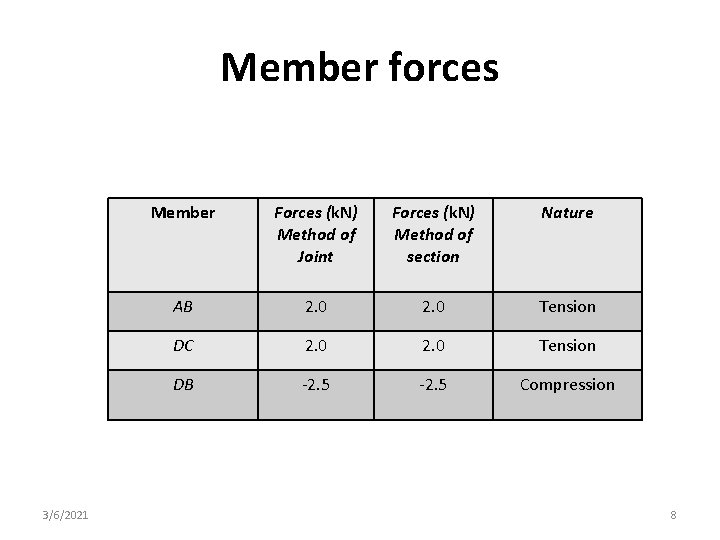
Member forces 3/6/2021 Member Forces (k. N) Method of Joint Forces (k. N) Method of section Nature AB 2. 0 Tension DC 2. 0 Tension DB -2. 5 Compression 8

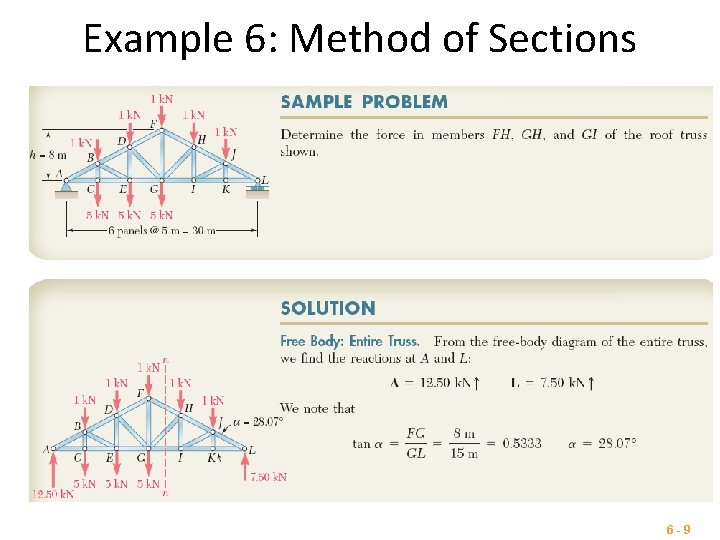
Example 6: Method of Sections 6 -9

Example 6 (continued): 6 - 10

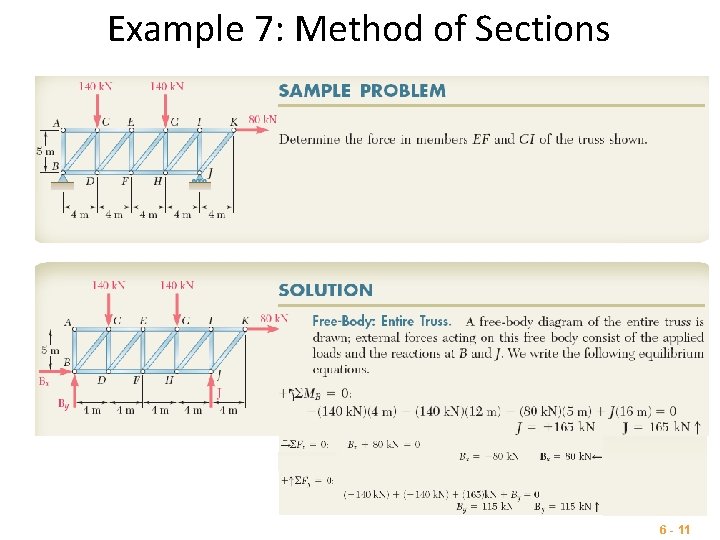
Example 7: Method of Sections 6 - 11

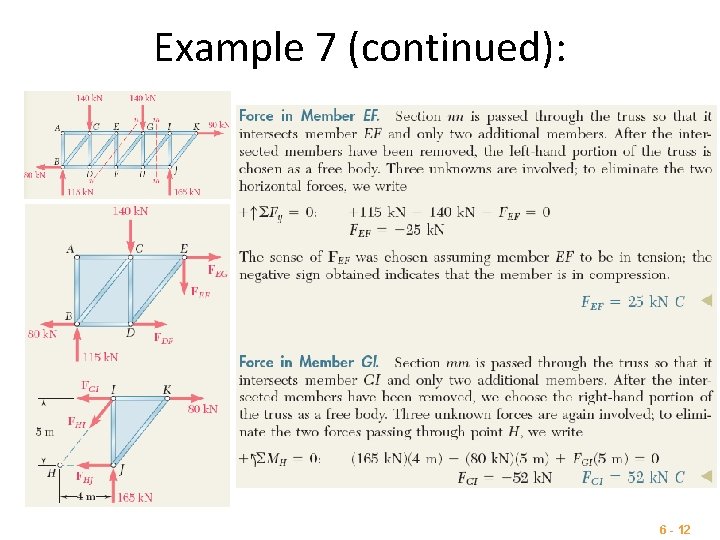
Example 7 (continued): 6 - 12







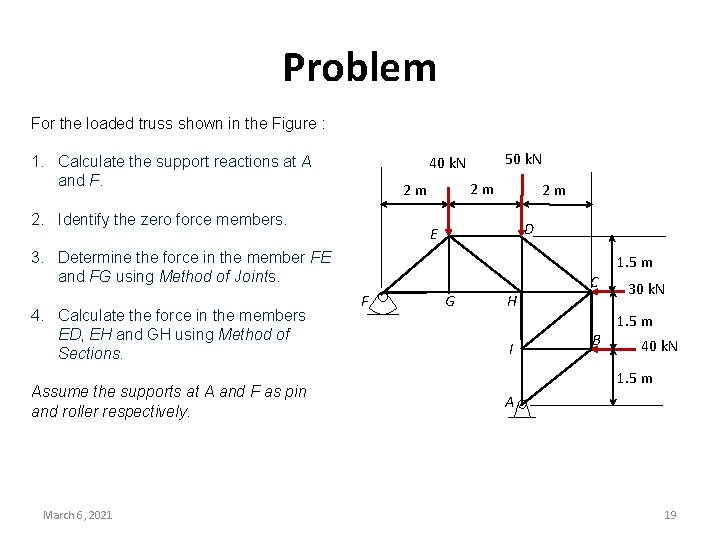
Problem For the loaded truss shown in the Figure : 1. Calculate the support reactions at A and F. 50 k. N 40 k. N 2 m 2 m 2. Identify the zero force members. 2 m D E 3. Determine the force in the member FE and FG using Method of Joints. 4. Calculate the force in the members ED, EH and GH using Method of Sections. Assume the supports at A and F as pin and roller respectively. March 6, 2021 F G H I C B 1. 5 m 30 k. N 1. 5 m 40 k. N 1. 5 m A 19

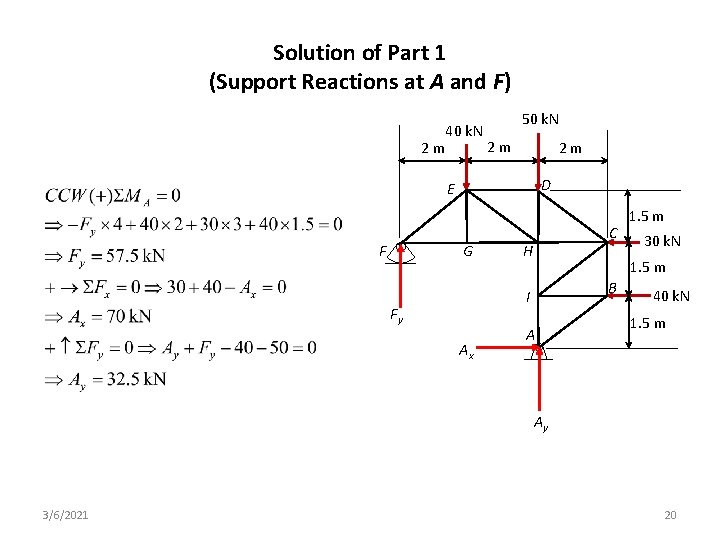
Solution of Part 1 (Support Reactions at A and F) 40 k. N 2 m 2 m 50 k. N 2 m D E F G C H Ax 30 k. N 1. 5 m B I Fy 1. 5 m A 40 k. N 1. 5 m Ay 3/6/2021 20

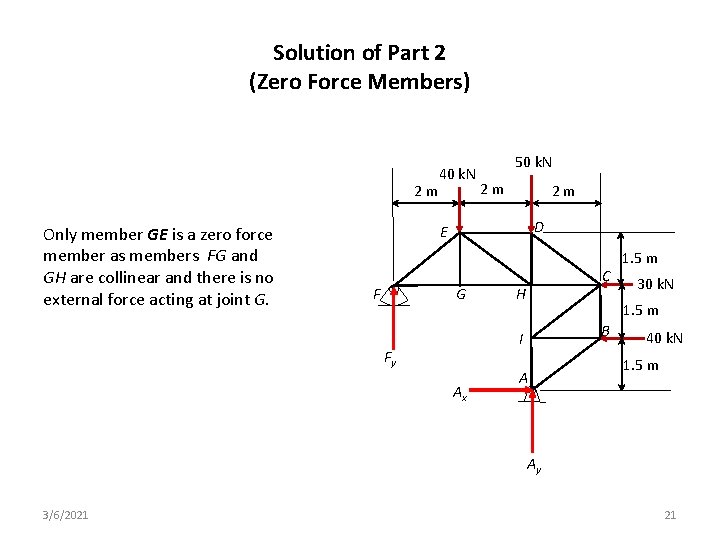
Solution of Part 2 (Zero Force Members) 40 k. N 2 m 2 m Only member GE is a zero force member as members FG and GH are collinear and there is no external force acting at joint G. 50 k. N 2 m D E G F C H Ax 30 k. N 1. 5 m B I Fy 1. 5 m A 40 k. N 1. 5 m Ay 3/6/2021 21

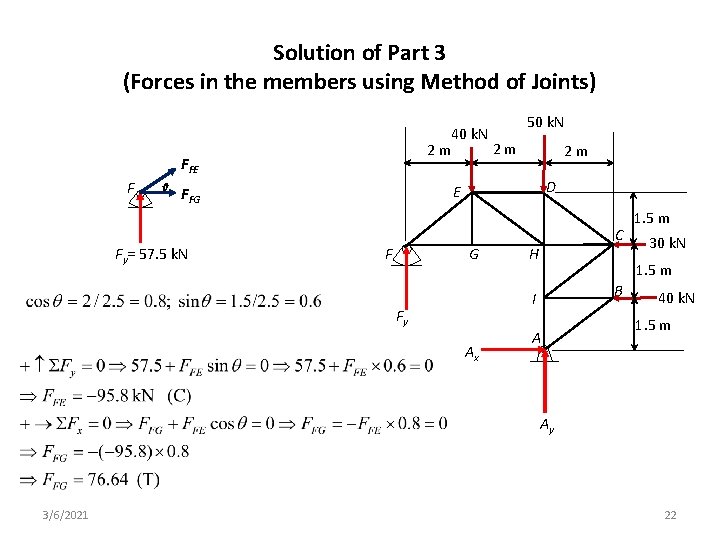
Solution of Part 3 (Forces in the members using Method of Joints) 40 k. N 2 m 2 m FFE F θ 2 m D E FFG Fy= 57. 5 k. N 50 k. N G F C H Ax 30 k. N 1. 5 m B I Fy 1. 5 m A 40 k. N 1. 5 m Ay 3/6/2021 22

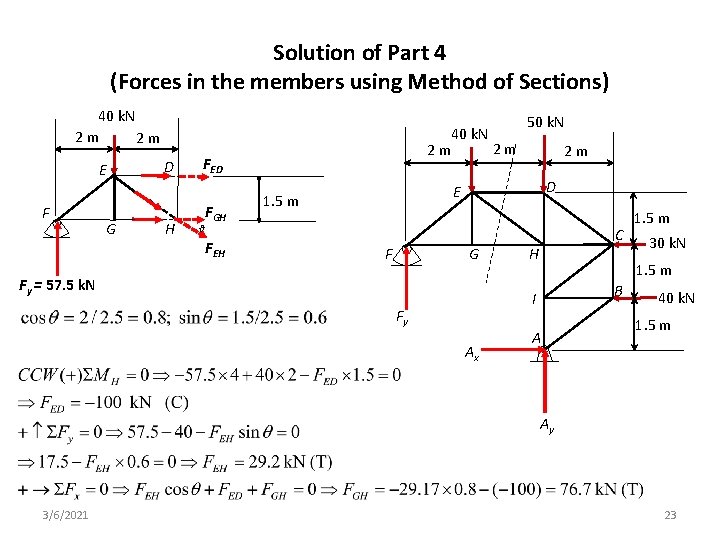
Solution of Part 4 (Forces in the members using Method of Sections) 40 k. N 2 m 2 m E F G D H 40 k. N 2 m 2 m FED FGH 50 k. N 2 m D E 1. 5 m θ FEH G F Fy = 57. 5 k. N C H Ax 30 k. N 1. 5 m B I Fy 1. 5 m A 40 k. N 1. 5 m Ay 3/6/2021 23


 Method of sections example
Method of sections example Method of sections example
Method of sections example Method of sections
Method of sections Objectives of symposium
Objectives of symposium Volume of solids with known cross sections
Volume of solids with known cross sections Think on these things
Think on these things Declaration of independence sections
Declaration of independence sections Lesson 4 declaring independence
Lesson 4 declaring independence Ctd ich
Ctd ich Gastric arteries
Gastric arteries Sectional plane are represented by
Sectional plane are represented by Sections of solids
Sections of solids Cutaways and cross sections definition
Cutaways and cross sections definition Revolved section
Revolved section Parts of the pharynx
Parts of the pharynx Cobol 1959
Cobol 1959 Pga sections map
Pga sections map Parabolas in the real world
Parabolas in the real world Rotating conic sections
Rotating conic sections Lesson 1 exploring conic sections
Lesson 1 exploring conic sections Aristotle anatomy
Aristotle anatomy Volumes with known cross sections
Volumes with known cross sections Parabola eiffel tower
Parabola eiffel tower Yellow section of erg
Yellow section of erg Anatomy terms
Anatomy terms Cross slice
Cross slice