Math 307 Spring 2003 Hentzel Time 1 10


![Theorem: If A n x n is any square matrix, then Det[A] = n+1 Theorem: If A n x n is any square matrix, then Det[A] = n+1](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-3.jpg)
![Proof Det [A] = SUM sgn(p) a 1 p(1) a 2 p(2). . . Proof Det [A] = SUM sgn(p) a 1 p(1) a 2 p(2). . .](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-4.jpg)

![Det[A] = SUM sgn(p) a 1 p(1) a 2 p(2) …a n p(n) p Det[A] = SUM sgn(p) a 1 p(1) a 2 p(2) …a n p(n) p](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-6.jpg)
![Det[A] = SUM sgn(p) a 11 a 2 p(2). . . a n p(n) Det[A] = SUM sgn(p) a 11 a 2 p(2). . . a n p(n)](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-7.jpg)
![Det[A] = a 11 SUM sgn(p) a 2 p(2). . . a n p(n) Det[A] = a 11 SUM sgn(p) a 2 p(2). . . a n p(n)](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-8.jpg)
![These SUMS are close to Det[Aij]. The only difference is that the sgn(p) is These SUMS are close to Det[Aij]. The only difference is that the sgn(p) is](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-9.jpg)
![Det[A] = a 11 Det[A 11] - a 12 Det[A 12] + a 13 Det[A] = a 11 Det[A 11] - a 12 Det[A 12] + a 13](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-10.jpg)
![n Theorem: Det[A] = Sum (-1) i+j aij Det[Aij] j=1 th Proof: This is n Theorem: Det[A] = Sum (-1) i+j aij Det[Aij] j=1 th Proof: This is](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-11.jpg)

![This can be written as Det[A] = SUM (-1) i+j-2 aij Det[Aij] Which can This can be written as Det[A] = SUM (-1) i+j-2 aij Det[Aij] Which can](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-13.jpg)
![Definition: Given a matrix A, then |+Det [A 11] |-Det [A 12] Adj(A) =|+Det Definition: Given a matrix A, then |+Det [A 11] |-Det [A 12] Adj(A) =|+Det](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-14.jpg)
![Theorem: A Adj(A) = Adj(A) A = Det[A] I Theorem: A Adj(A) = Adj(A) A = Det[A] I](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-15.jpg)


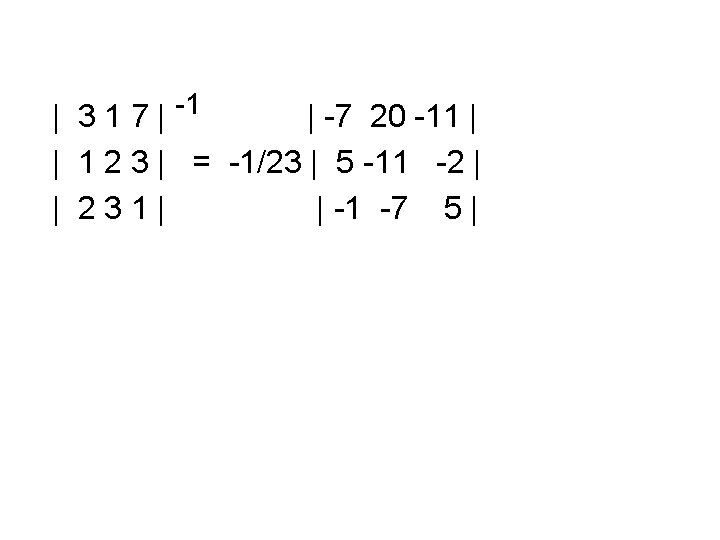
![Theorem: Det[A] = Det[AT] Proof: Since (A-1)T = (AT) -1 If A is invertible, Theorem: Det[A] = Det[AT] Proof: Since (A-1)T = (AT) -1 If A is invertible,](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-19.jpg)

![Find the Determinant of differentiation on the space with basis Sinh[x] Cosh[x]. Sinh[x] 0 Find the Determinant of differentiation on the space with basis Sinh[x] Cosh[x]. Sinh[x] 0](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-21.jpg)








- Slides: 29

Math 307 Spring, 2003 Hentzel Time: 1: 10 -2: 00 MWF Room: 1324 Howe Hall Instructor: Irvin Roy Hentzel Office 432 Carver Phone 515 -294 -8141 E-mail: hentzel@iastate. edu http: //www. math. iastate. edu/hentzel/class. 307. ICN Text: Linear Algebra With Applications, Second Edition Otto Bretscher

Friday, April 4 Chapter 6. 2 Page 266 Problem 4, 14, 46, 48 Main Idea: Expand along any row or column. Key Words: Adjoint, Aij Det[A] = SUM sgn(p) a 1 p(1) a 2 p(2). . . a n p(n) all p Goal: Learn how to expand a determinant.
![Theorem If A n x n is any square matrix then DetA n1 Theorem: If A n x n is any square matrix, then Det[A] = n+1](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-3.jpg)
Theorem: If A n x n is any square matrix, then Det[A] = n+1 a 11 Det[A 11] - a 12 Det[A 12]+. . . +(-1) Det[A 1 n] Where Aij is the n-1 x n-1 matrix obtained by deleting row i and column j from A.
![Proof Det A SUM sgnp a 1 p1 a 2 p2 Proof Det [A] = SUM sgn(p) a 1 p(1) a 2 p(2). . .](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-4.jpg)
Proof Det [A] = SUM sgn(p) a 1 p(1) a 2 p(2). . . a n p(n) all p There are n possible choices for a 1 p(1). One can choose any element from the top row. The possibilities are a 11, a 12, . . . a 1 n.

We split up the sum into n parts depending on which element was chosen from the top row.
![DetA SUM sgnp a 1 p1 a 2 p2 a n pn p Det[A] = SUM sgn(p) a 1 p(1) a 2 p(2) …a n p(n) p](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-6.jpg)
Det[A] = SUM sgn(p) a 1 p(1) a 2 p(2) …a n p(n) p (1)=1 + SUM sgn(p) a 1 p(1) a 2 p(2) . . a n p(n) p(1)=2 + SUM sgn(p) a 1 p(1) a 2 p(2) p(1)=3 … a n p(n) : + SUM sgn(p) a 1 p(1) a 2 p(2) … a n p(n) p(1)=n
![DetA SUM sgnp a 11 a 2 p2 a n pn Det[A] = SUM sgn(p) a 11 a 2 p(2). . . a n p(n)](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-7.jpg)
Det[A] = SUM sgn(p) a 11 a 2 p(2). . . a n p(n) p(1) = 1 + SUM sgn(p) a 12 a 2 p(2). . . a n p(n) p(1) = 2 + SUM sgn(p) a 13 a 2 p(2). . . a n p(n) p(1) = 3 : + SUM p(1) = n sgn(p) a 1 n a 2 p(2). . . a n p(n)
![DetA a 11 SUM sgnp a 2 p2 a n pn Det[A] = a 11 SUM sgn(p) a 2 p(2). . . a n p(n)](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-8.jpg)
Det[A] = a 11 SUM sgn(p) a 2 p(2). . . a n p(n) p(1) = 1 + a 12 SUM sgn(p) a 2 p(2). . . a n p(n) p(1) = 2 + a 13 SUM p(1) = 3 + a 1 n SUM p(1) = n sgn(p) a 2 p(2). . . a n p(n) : sgn(p) a 2 p(2). . . a n p(n)
![These SUMS are close to DetAij The only difference is that the sgnp is These SUMS are close to Det[Aij]. The only difference is that the sgn(p) is](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-9.jpg)
These SUMS are close to Det[Aij]. The only difference is that the sgn(p) is based on all n positions of p(1) p(2) p(3). . . p(n). In Det [A ij] the sgn is based on n-1 positions of p(2) p(3). . . p(n).
![DetA a 11 DetA 11 a 12 DetA 12 a 13 Det[A] = a 11 Det[A 11] - a 12 Det[A 12] + a 13](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-10.jpg)
Det[A] = a 11 Det[A 11] - a 12 Det[A 12] + a 13 Det[A 13]. . (-1)n+1 a 1 n Det[A 1 n]
![n Theorem DetA Sum 1 ij aij DetAij j1 th Proof This is n Theorem: Det[A] = Sum (-1) i+j aij Det[Aij] j=1 th Proof: This is](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-11.jpg)
n Theorem: Det[A] = Sum (-1) i+j aij Det[Aij] j=1 th Proof: This is expansion by the i row.

We first interchange rows i-1 times to move th the i row to the first row. Then we expand along the first row. This gives | ai 1 Det[Ai 1] | | Det[A]=(-1)i-1 | - a i 2 Det[Ai 2] | + ai 3 Det[Ai 3] | | : | n+1 | (-1) ain Det[Ain] |
![This can be written as DetA SUM 1 ij2 aij DetAij Which can This can be written as Det[A] = SUM (-1) i+j-2 aij Det[Aij] Which can](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-13.jpg)
This can be written as Det[A] = SUM (-1) i+j-2 aij Det[Aij] Which can be simplified since (-1)2 = 1 to Det[A] = SUM (-1)i+j aij Det[Aij]
![Definition Given a matrix A then Det A 11 Det A 12 AdjA Det Definition: Given a matrix A, then |+Det [A 11] |-Det [A 12] Adj(A) =|+Det](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-14.jpg)
Definition: Given a matrix A, then |+Det [A 11] |-Det [A 12] Adj(A) =|+Det [A 13] |-Det [A 14] |. |. |. - Det [A 21] + Det [A 22] - Det [A 23] + Det [A 24]. . . +Det [A 31]. . | -Det [A 32]. . | +Det [A 33]. . | -Det [A 34]. . |. |
![Theorem A AdjA AdjA A DetA I Theorem: A Adj(A) = Adj(A) A = Det[A] I](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-15.jpg)
Theorem: A Adj(A) = Adj(A) A = Det[A] I

Find the inverse of | 317| | 123| | 231|

check T |3 1 7| | -7 (-5) -1| |-7 20 -11| | -23 0 0| Adj|1 2 3| =|(-20)-11 (7)| = |5 -11 -2 | | 0 -23 0| |2 3 1| | -11 (2) 5 | | -1 -7 5| | 0 0 -23 |
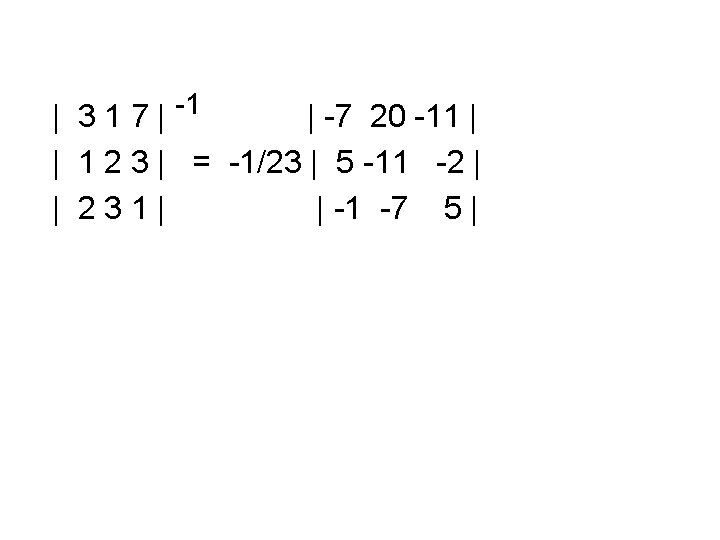
| 3 1 7 | -1 | -7 20 -11 | | 1 2 3 | = -1/23 | 5 -11 -2 | | 231| | -1 -7 5 |
![Theorem DetA DetAT Proof Since A1T AT 1 If A is invertible Theorem: Det[A] = Det[AT] Proof: Since (A-1)T = (AT) -1 If A is invertible,](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-19.jpg)
Theorem: Det[A] = Det[AT] Proof: Since (A-1)T = (AT) -1 If A is invertible, then A is a product of Elementary Row Operation Matrices. For Elementary Row Operation Matrices Det [ET] = Det [E], we have Det [A] = Det[AT]. If A is not invertible, then neither is AT T and Det [A] = Det[A ] = 0.

Theorem: The determinant of a linear transformation is invariant under change of basis. Proof: Det [ P -1 A P] = Det[P-1] Det [A] Det [P] = Det[ P-1 P] Det [A] = Det [A].
![Find the Determinant of differentiation on the space with basis Sinhx Coshx Sinhx 0 Find the Determinant of differentiation on the space with basis Sinh[x] Cosh[x]. Sinh[x] 0](https://slidetodoc.com/presentation_image/fabd5120065905e848d0cf39e173d3dd/image-21.jpg)
Find the Determinant of differentiation on the space with basis Sinh[x] Cosh[x]. Sinh[x] 0 Cosh[x] 1 0 Det[ derivation ] = -1.

Find the Determinant of differentiation on the x -x space with basis e , e. ex e -x ex 1 0 e -x 0 -1 Det [ derivation ] = -1.

Page 263 Example 8. A= |1012| |9130| |9220| |5003| Find the determinant of A.

Add -2 Row 2 to row 3 |1012| |9130| |-9 0 -4 0 | |5003|

Expand along second column |1 +1 | |-9 |5 1 2| | -4 0 | 0 3|

Add 4 Row 1 to Row 2 |1 +1 | |-5 |5 12| | 08| 03|

Expand along column 2 | (-1) | |-5 |5 | | 8| 3| Evaluate the final 2 x 2 determinant. -(-15 - 40) = 55.

Page 265 Problem 5. |11111| |12222| A=|11333| |11144| |11115| Find the determinant of A.

Eliminate the first column |11111| |01111| A=|00222| |00033| |00004| The determinant of a triangular matrix is the product of the elements on the diagonal. Det [A] = 24.