Logistic regression Analysis of proportion data We know

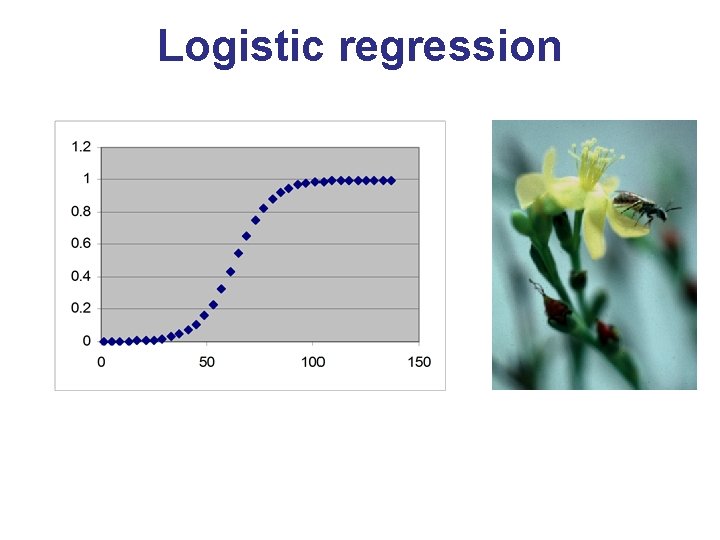
Logistic regression

Analysis of proportion data • We know how many times an event occurred, and how many times it did not occur. • We want to know if these proportions are affected by a treatment or a factor. • Examples: Proportion dying Proportion responding to a treatment Proportion in a sex Proportion flowering

The old fashioned way • People used to model these data using percentages as the response variable… • The problems with this are: • Errors are not normally distributed! • The variance is not constant! • The response is bounded (0 -1)! • We lose information on the sample size!

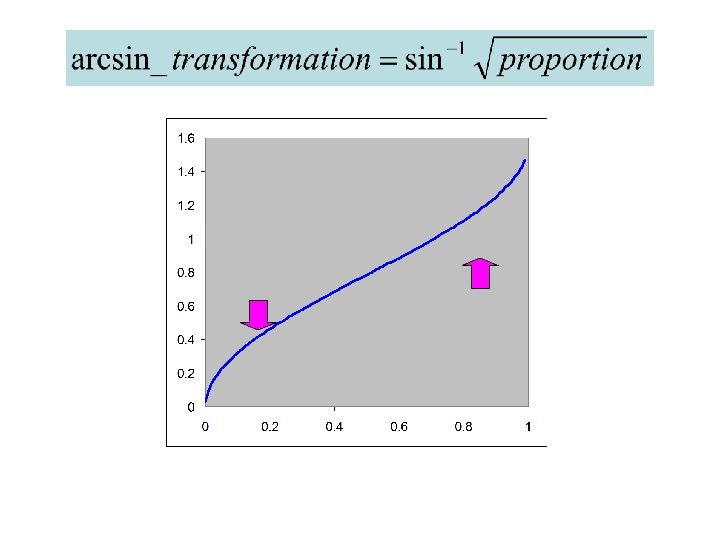
However… • Some data, such as percentage of plant cover, is better analyzed using the conventional models (normal errors and constant variance) following the arcsine transformation (the response variable measured in radians)…

If the response variable takes the form of percentage change of some measurement Usually it is better to: • Analysis of covariance, using final weight as the response variable and initial weight as the covariate • Specifying the response variable as a relative growth rate, measured as log(final/initial) Both can be analyzed with normal errors without further transformations!

Rational for logistic regression • The traditional transformation of proportion data was arcsine. This transformation took care of the error distribution. There is nothing wrong with this transformation, but a simpler approach is often preferable, and is likely to produce a model that is easier to interpret…

The logistic curve • The logistic curve is commonly used to describe data on proportions. • It asymptotes at 0 and 1, so that negative proportions and responses of more than 100 % cannot be predicted.

Binomial errors • If p = proportion of individuals observed to respond in a given way • The proportion of individuals that respond in alternative ways is: 1 -p and we shall call this proportion q • n is the size of the sample (or number of attempts) • An important point is that the variance of the binomial distribution is not constant. In fact the variance of a binomial distribution with mean np is: So that the variance changes with the mean like this:

The logistic model for p as a function of x is given by: This model is bounded since:

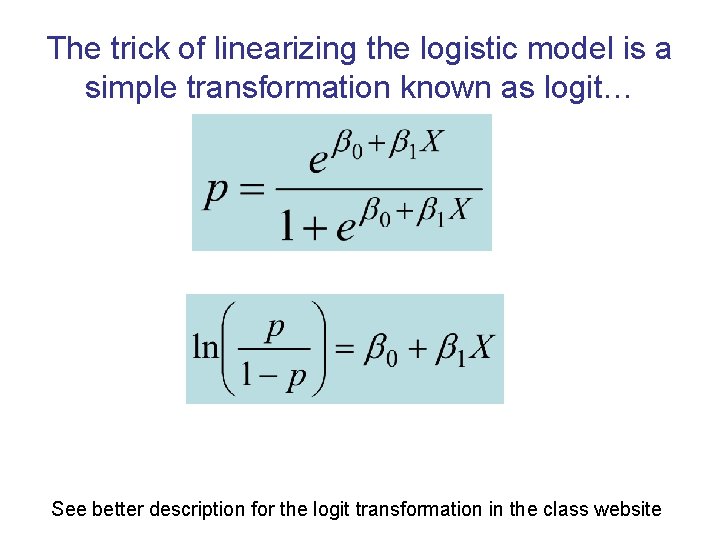
The trick of linearizing the logistic model is a simple transformation known as logit… See better description for the logit transformation in the class website

Hypericum cumulicola • Small short-lived perennial herb • Narrowly endemic and endangered • Flowers are small and bisexual • Self-compatible, but requires pollinators to set seed Menges et al. (1999) Dolan et al. (1999) Boyle and Menges (2001)

Demographic data • 15 populations (various patch sizes) • >80 individuals per population each year • Data on height and number of reproductive structures • Survival between August 1994 and August 1995

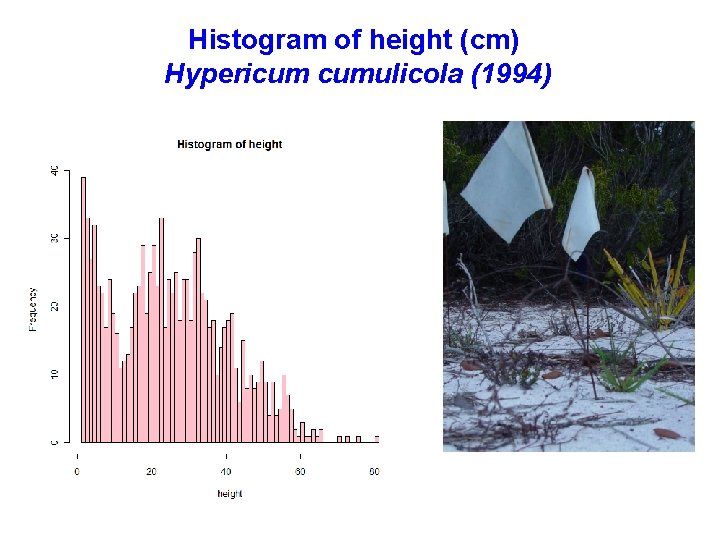
Histogram of height (cm) Hypericum cumulicola (1994)

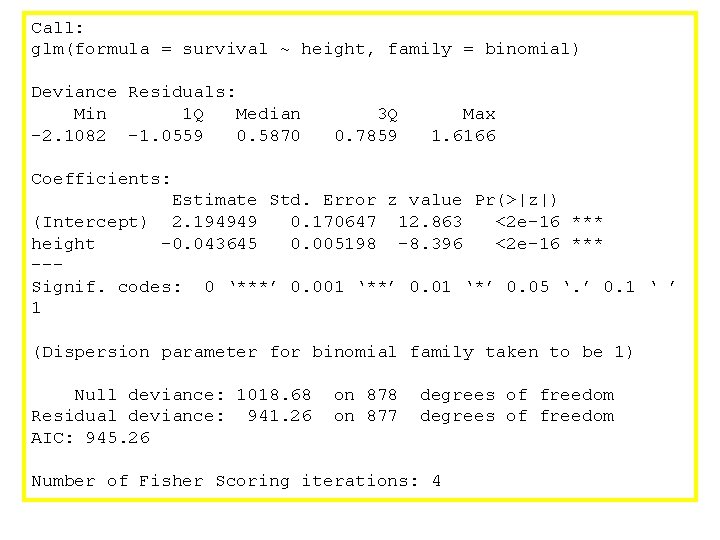
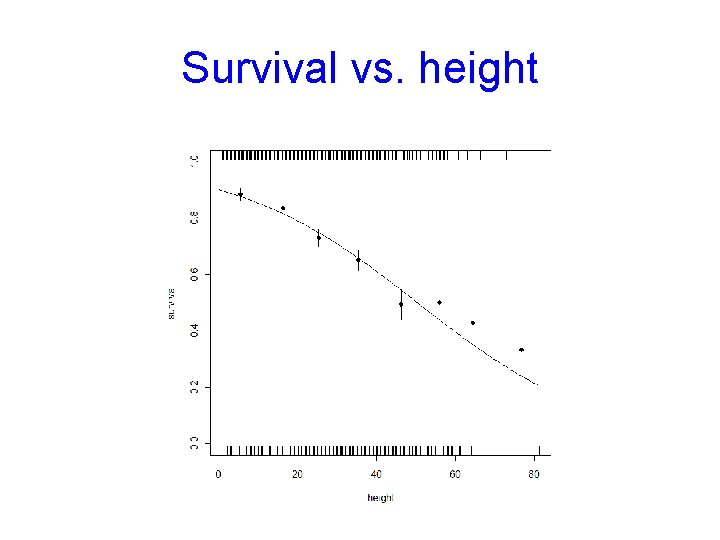
Call: glm(formula = survival ~ height, family = binomial) Deviance Residuals: Min 1 Q Median -2. 1082 -1. 0559 0. 5870 3 Q 0. 7859 Max 1. 6166 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 2. 194949 0. 170647 12. 863 <2 e-16 *** height -0. 043645 0. 005198 -8. 396 <2 e-16 *** --Signif. codes: 0 ‘***’ 0. 001 ‘**’ 0. 01 ‘*’ 0. 05 ‘. ’ 0. 1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1018. 68 Residual deviance: 941. 26 AIC: 945. 26 on 878 on 877 degrees of freedom Number of Fisher Scoring iterations: 4

Calculating a given proportion You can back-transform from logits (z) to proportions (p) by:

Survival vs. height

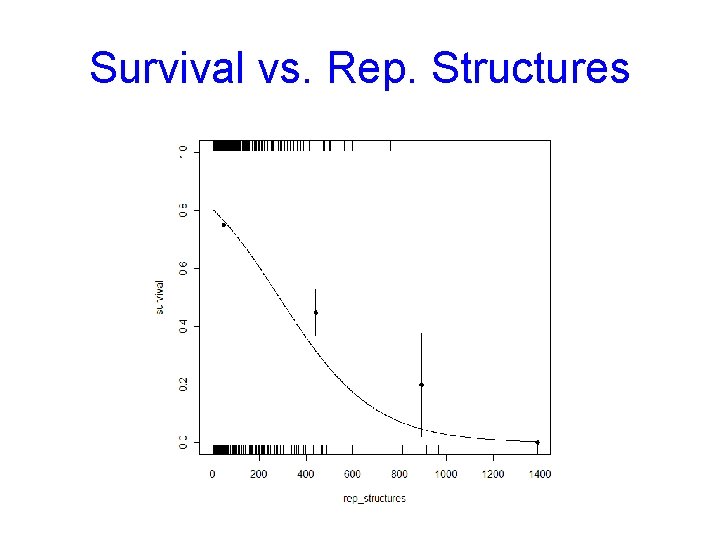
Survival vs. Rep. Structures