LO SPAZIO EUCLIDEO Lo spazio euclideo un insieme

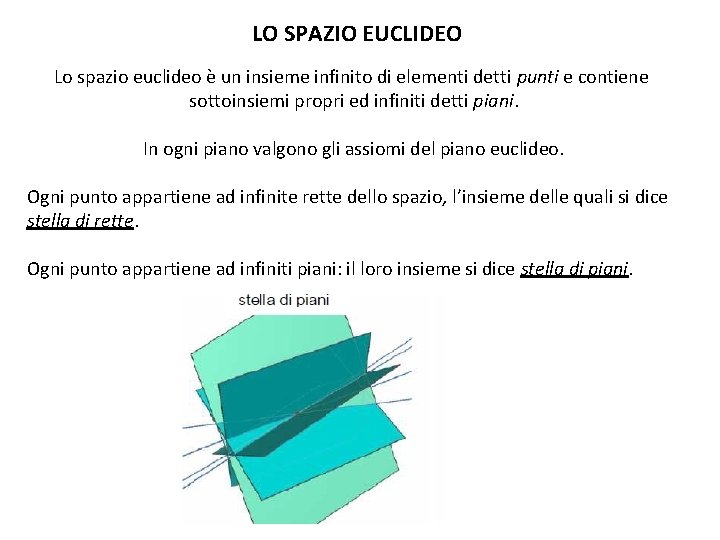
LO SPAZIO EUCLIDEO Lo spazio euclideo è un insieme infinito di elementi detti punti e contiene sottoinsiemi propri ed infiniti detti piani. In ogni piano valgono gli assiomi del piano euclideo. Ogni punto appartiene ad infinite rette dello spazio, l’insieme delle quali si dice stella di rette. Ogni punto appartiene ad infiniti piani: il loro insieme si dice stella di piani.

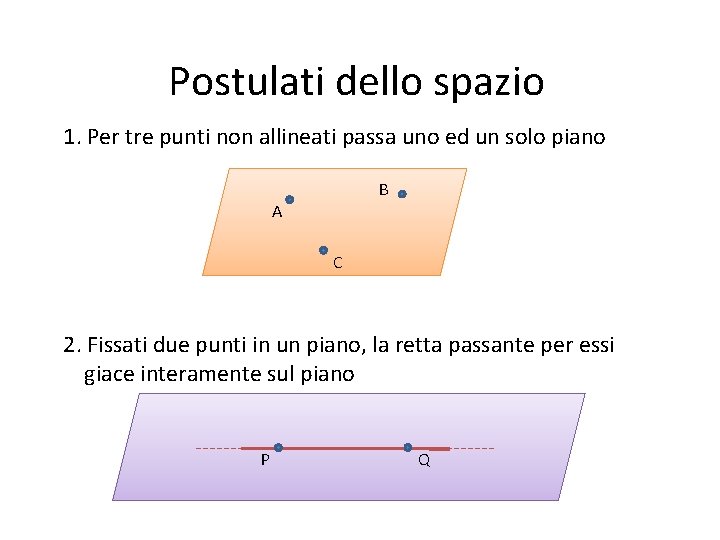
Postulati dello spazio 1. Per tre punti non allineati passa uno ed un solo piano B A C 2. Fissati due punti in un piano, la retta passante per essi giace interamente sul piano P Q

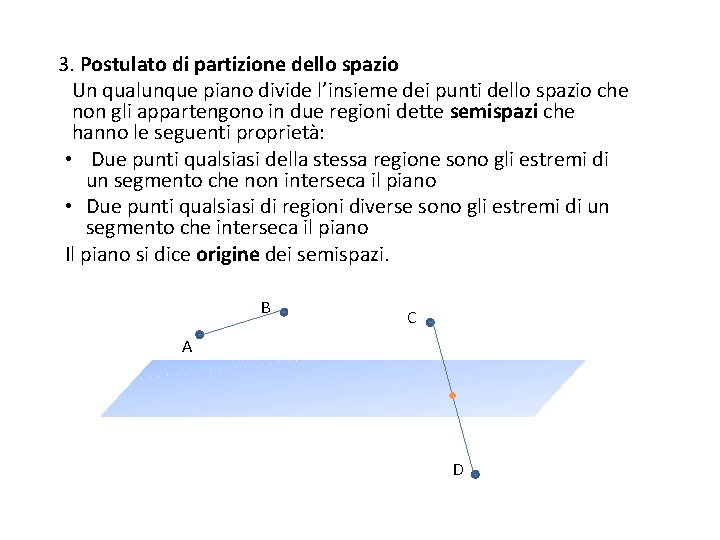
3. Postulato di partizione dello spazio Un qualunque piano divide l’insieme dei punti dello spazio che non gli appartengono in due regioni dette semispazi che hanno le seguenti proprietà: • Due punti qualsiasi della stessa regione sono gli estremi di un segmento che non interseca il piano • Due punti qualsiasi di regioni diverse sono gli estremi di un segmento che interseca il piano Il piano si dice origine dei semispazi. B C A D

La posizione di due rette nello spazio • Se due rette nello spazio appartengono a uno stesso piano, si dicono complanari. Due rette complanari possono essere incidenti o parallele. • Se due rette non sono complanari, si dicono sghembe.

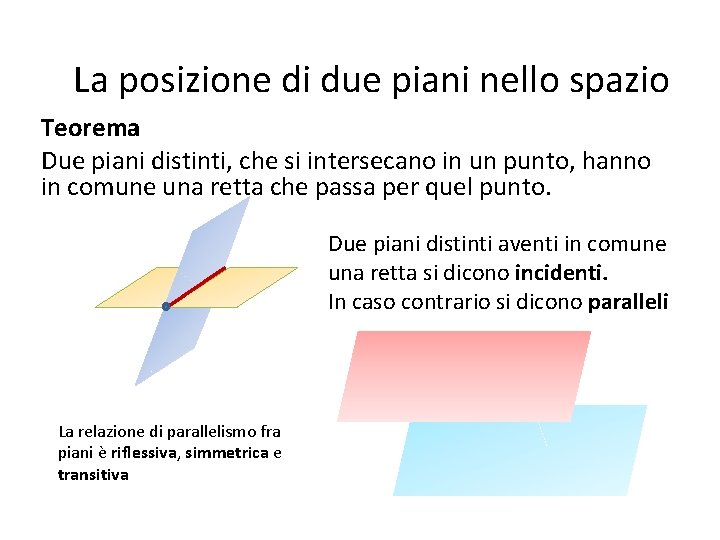
La posizione di due piani nello spazio Teorema Due piani distinti, che si intersecano in un punto, hanno in comune una retta che passa per quel punto. Due piani distinti aventi in comune una retta si dicono incidenti. In caso contrario si dicono paralleli La relazione di parallelismo fra piani è riflessiva, simmetrica e transitiva

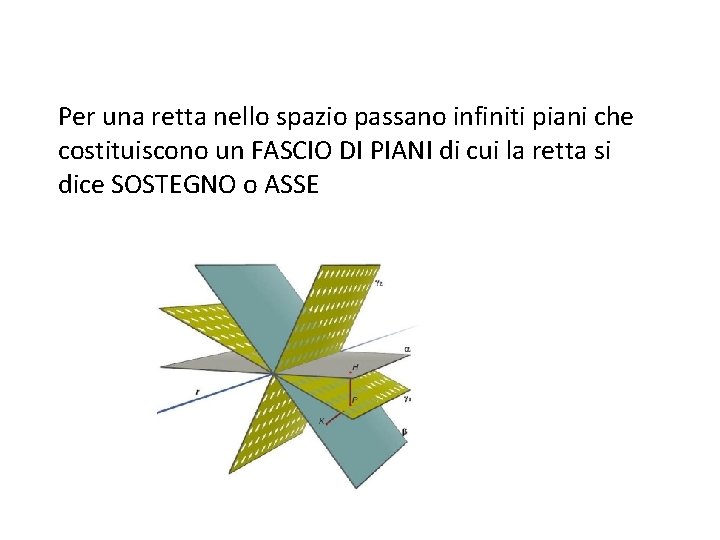
Per una retta nello spazio passano infiniti piani che costituiscono un FASCIO DI PIANI di cui la retta si dice SOSTEGNO o ASSE

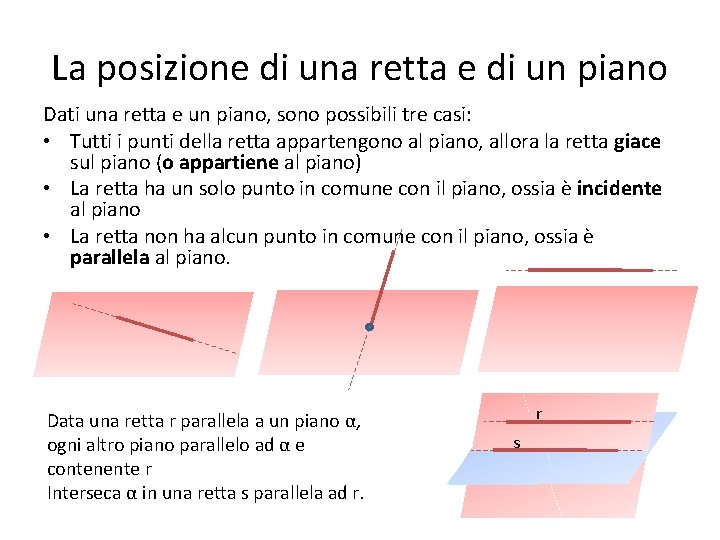
La posizione di una retta e di un piano Dati una retta e un piano, sono possibili tre casi: • Tutti i punti della retta appartengono al piano, allora la retta giace sul piano (o appartiene al piano) • La retta ha un solo punto in comune con il piano, ossia è incidente al piano • La retta non ha alcun punto in comune con il piano, ossia è parallela al piano. Data una retta r parallela a un piano α, ogni altro piano parallelo ad α e contenente r Interseca α in una retta s parallela ad r. r s α

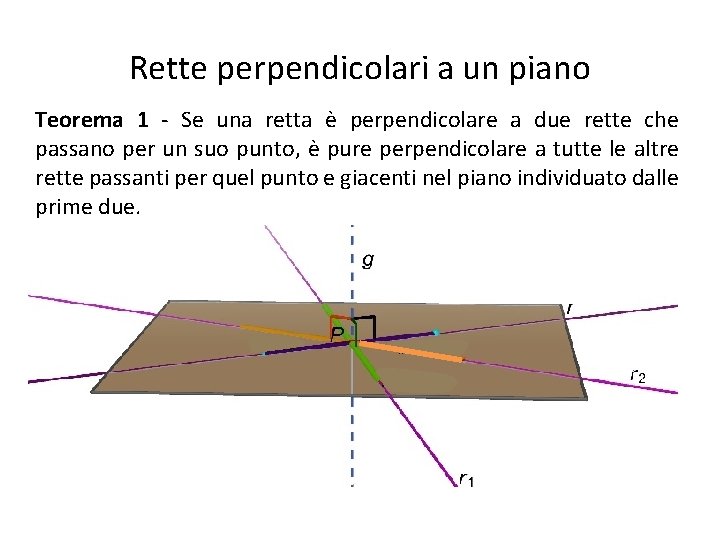
Rette perpendicolari a un piano Teorema 1 - Se una retta è perpendicolare a due rette che passano per un suo punto, è pure perpendicolare a tutte le altre rette passanti per quel punto e giacenti nel piano individuato dalle prime due.

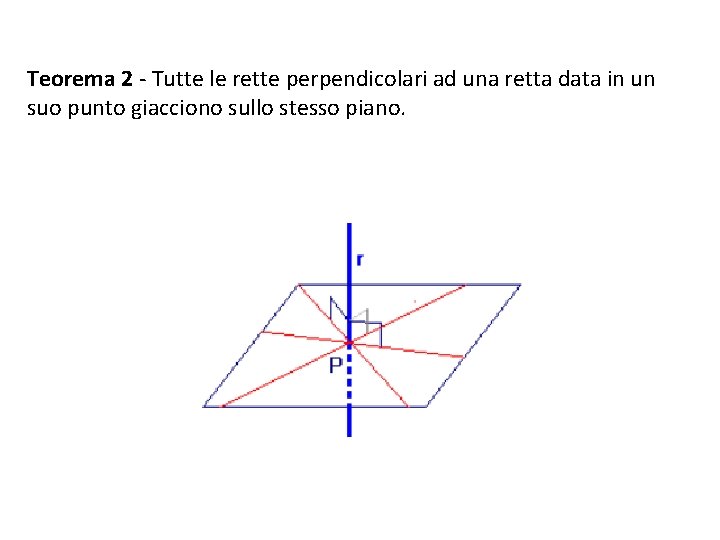
Teorema 2 - Tutte le rette perpendicolari ad una retta data in un suo punto giacciono sullo stesso piano.

Retta e piano perpendicolari Ora siamo in grado di dare la definizione di retta e piano perpendicolari: una retta ed un piano si dicono perpendicolari quando la retta interseca il piano ed è perpendicolare a tutte le rette del piano che passano per il punto di intersezione, detto piede della perpendicolare. E’ ovvio che: • Dati un punto e una retta, esiste un solo piano passante per il punto e perpendicolare alla retta. • Piani perpendicolari alla stessa retta sono paralleli tra loro. Rette perpendicolari allo stesso piano sono parallele tra loro. • Dati un punto e un piano, esiste una sola retta passante per il punto e perpendicolare al piano.

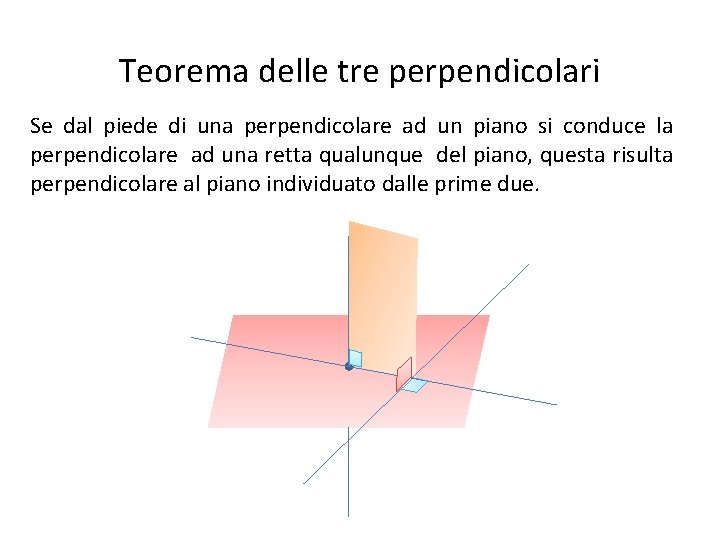
Teorema delle tre perpendicolari Se dal piede di una perpendicolare ad un piano si conduce la perpendicolare ad una retta qualunque del piano, questa risulta perpendicolare al piano individuato dalle prime due.

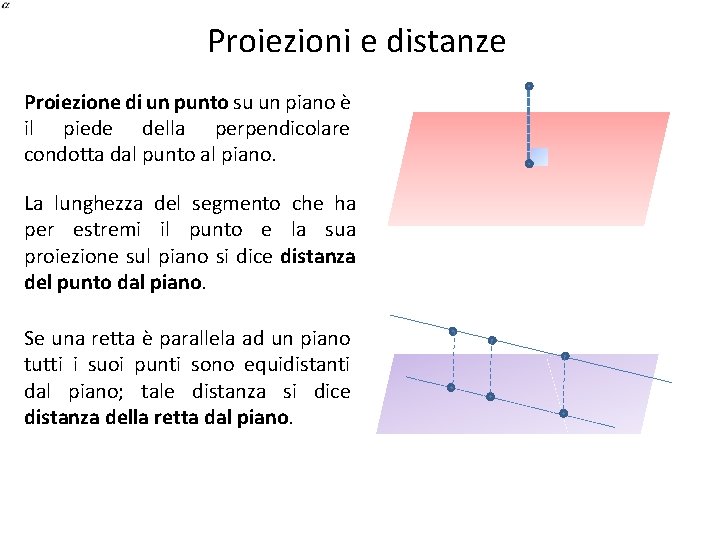
Proiezioni e distanze Proiezione di un punto su un piano è il piede della perpendicolare condotta dal punto al piano. La lunghezza del segmento che ha per estremi il punto e la sua proiezione sul piano si dice distanza del punto dal piano. Se una retta è parallela ad un piano tutti i suoi punti sono equidistanti dal piano; tale distanza si dice distanza della retta dal piano.

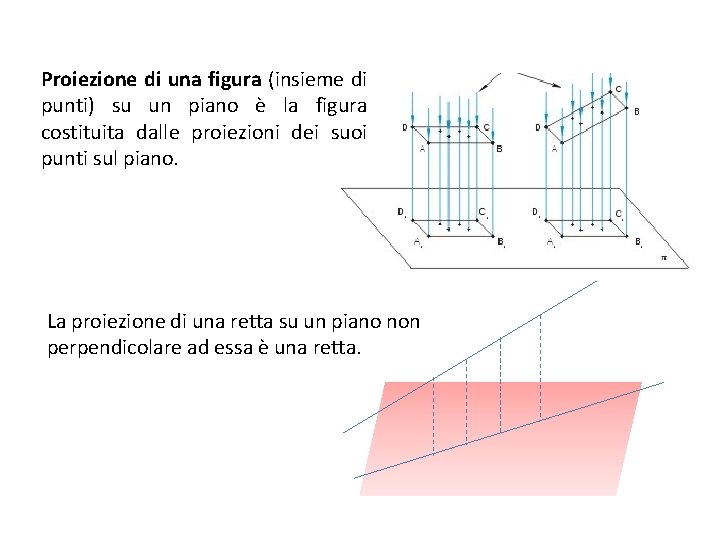
Proiezione di una figura (insieme di punti) su un piano è la figura costituita dalle proiezioni dei suoi punti sul piano. La proiezione di una retta su un piano non perpendicolare ad essa è una retta.

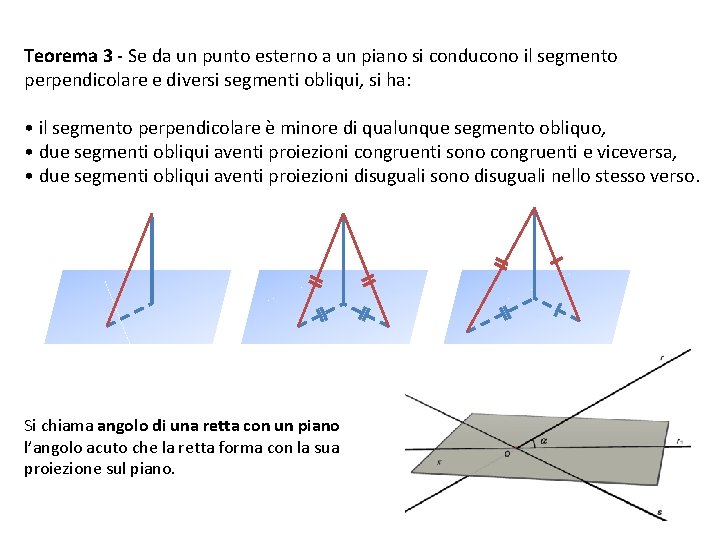
Teorema 3 - Se da un punto esterno a un piano si conducono il segmento perpendicolare e diversi segmenti obliqui, si ha: • il segmento perpendicolare è minore di qualunque segmento obliquo, • due segmenti obliqui aventi proiezioni congruenti sono congruenti e viceversa, • due segmenti obliqui aventi proiezioni disuguali sono disuguali nello stesso verso. Si chiama angolo di una retta con un piano l’angolo acuto che la retta forma con la sua proiezione sul piano.

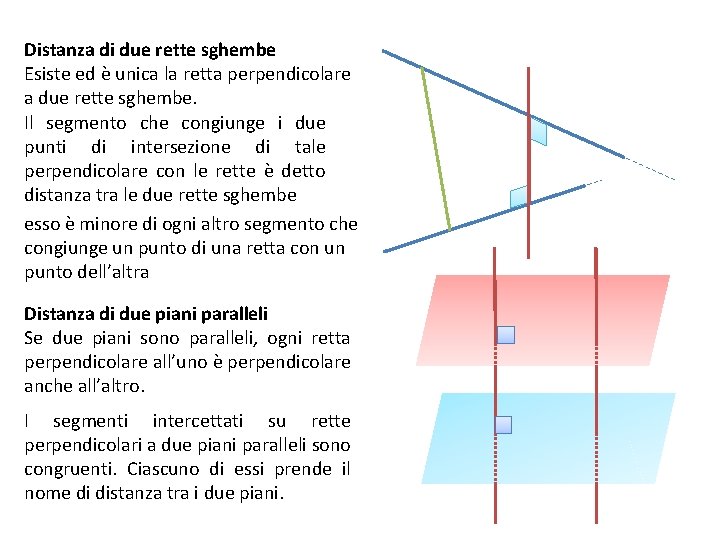
Distanza di due rette sghembe Esiste ed è unica la retta perpendicolare a due rette sghembe. Il segmento che congiunge i due punti di intersezione di tale perpendicolare con le rette è detto distanza tra le due rette sghembe esso è minore di ogni altro segmento che congiunge un punto di una retta con un punto dell’altra Distanza di due piani paralleli Se due piani sono paralleli, ogni retta perpendicolare all’uno è perpendicolare anche all’altro. I segmenti intercettati su rette perpendicolari a due piani paralleli sono congruenti. Ciascuno di essi prende il nome di distanza tra i due piani.

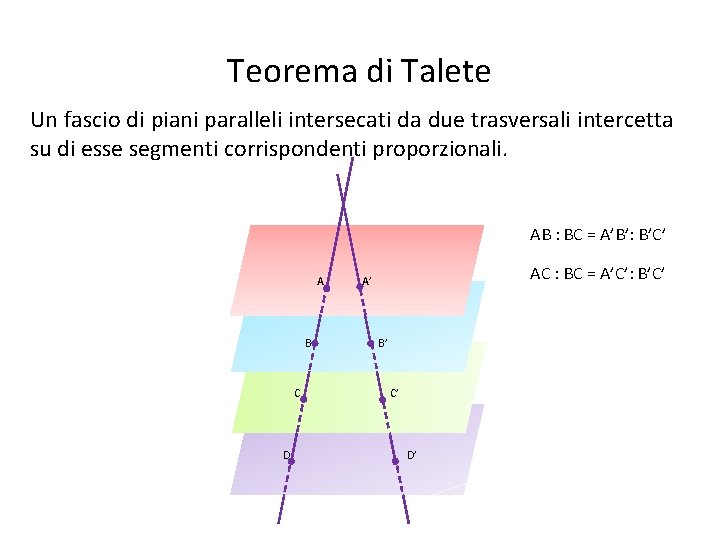
Teorema di Talete Un fascio di piani paralleli intersecati da due trasversali intercetta su di esse segmenti corrispondenti proporzionali. AB : BC = A’B’: B’C’ A B C D AC : BC = A’C’: B’C’ A’ B’ C’ D’