Linear Filtering Part II Selim Aksoy Department of

  • Slides: 45
Download presentation
Linear Filtering – Part II Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.

Linear Filtering – Part II Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs. bilkent. edu. tr

Fourier theory n Jean Baptiste Joseph Fourier had a crazy idea: Any periodic function

Fourier theory n Jean Baptiste Joseph Fourier had a crazy idea: Any periodic function can be written as a weighted sum of sines and cosines of different frequencies (1807). Fourier series n Even functions that are not periodic (but whose area under the curve is finite) can be expressed as the integral of sines and cosines multiplied by a weighing function. Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 2

Fourier theory n n The Fourier theory shows how most real functions can be

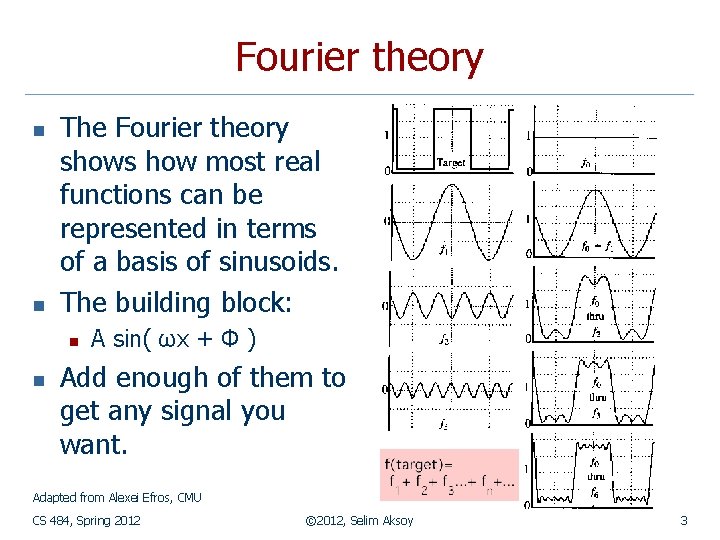
Fourier theory n n The Fourier theory shows how most real functions can be represented in terms of a basis of sinusoids. The building block: n n A sin( ωx + Φ ) Add enough of them to get any signal you want. Adapted from Alexei Efros, CMU CS 484, Spring 2012 © 2012, Selim Aksoy 3

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 4

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 4

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 5

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 5

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 6

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 6

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 7

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 7

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 8

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 8

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 9

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 9

Fourier transform To get some sense of what basis elements look like, we plot

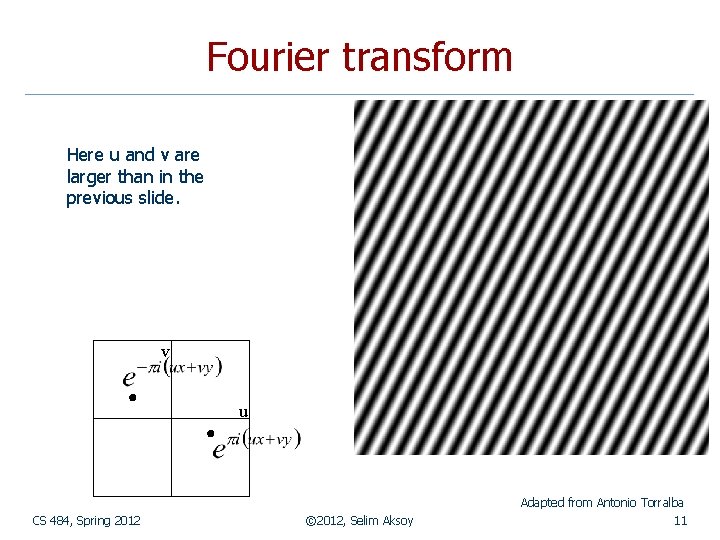
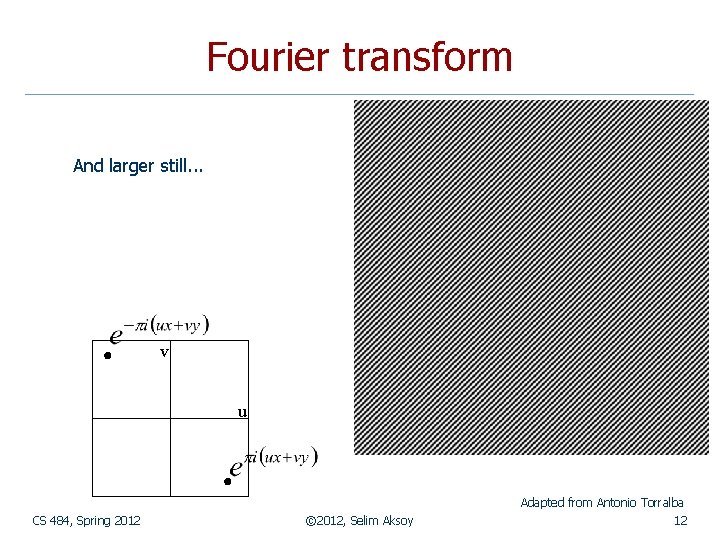
Fourier transform To get some sense of what basis elements look like, we plot a basis element --- or rather, its real part --as a function of x, y for some fixed u, v. We get a function that is constant when (ux+vy) is constant. The magnitude of the vector (u, v) gives a frequency, and its direction gives an orientation. The function is a sinusoid with this frequency along the direction, and constant perpendicular to the direction. v u Adapted from Antonio Torralba CS 484, Spring 2012 © 2012, Selim Aksoy 10

Fourier transform Here u and v are larger than in the previous slide. v

Fourier transform Here u and v are larger than in the previous slide. v u Adapted from Antonio Torralba CS 484, Spring 2012 © 2012, Selim Aksoy 11

Fourier transform And larger still. . . v u Adapted from Antonio Torralba CS

Fourier transform And larger still. . . v u Adapted from Antonio Torralba CS 484, Spring 2012 © 2012, Selim Aksoy 12

Fourier transform Adapted from Alexei Efros, CMU CS 484, Spring 2012 © 2012, Selim

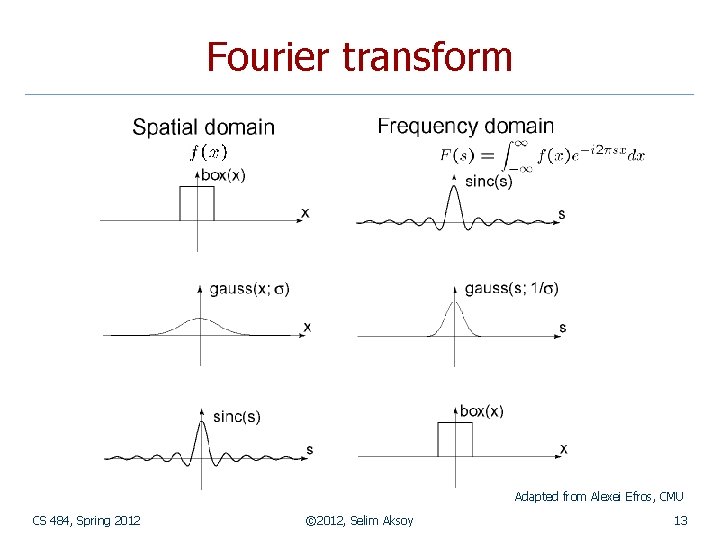
Fourier transform Adapted from Alexei Efros, CMU CS 484, Spring 2012 © 2012, Selim Aksoy 13

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and

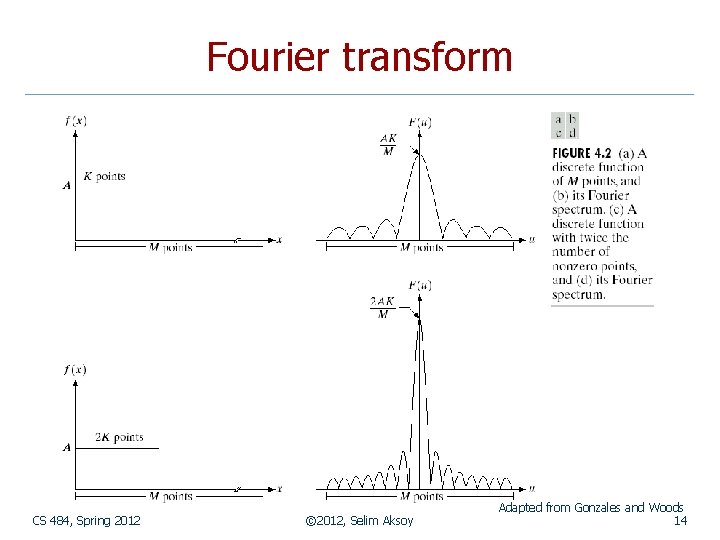
Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and Woods 14

Fourier transform Adapted from Gonzales and Woods CS 484, Spring 2012 © 2012, Selim

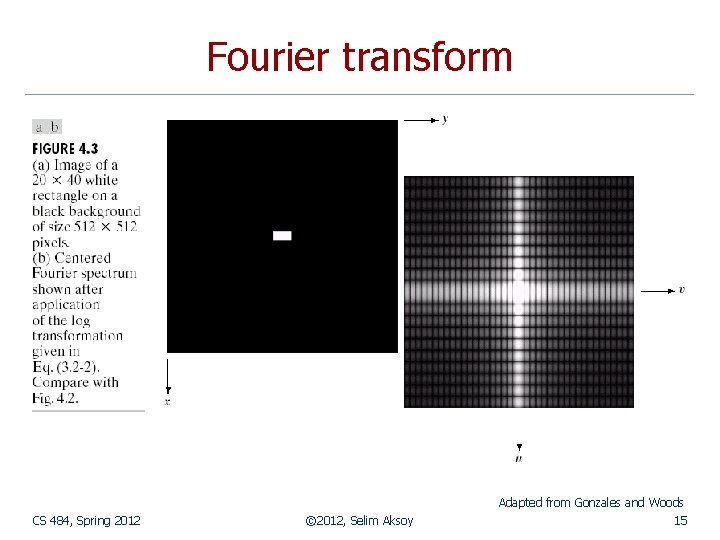
Fourier transform Adapted from Gonzales and Woods CS 484, Spring 2012 © 2012, Selim Aksoy 15

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 16

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 16

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 17

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy 17

Fourier transform How to interpret a Fourier spectrum: Vertical orientation Low spatial frequencies 45

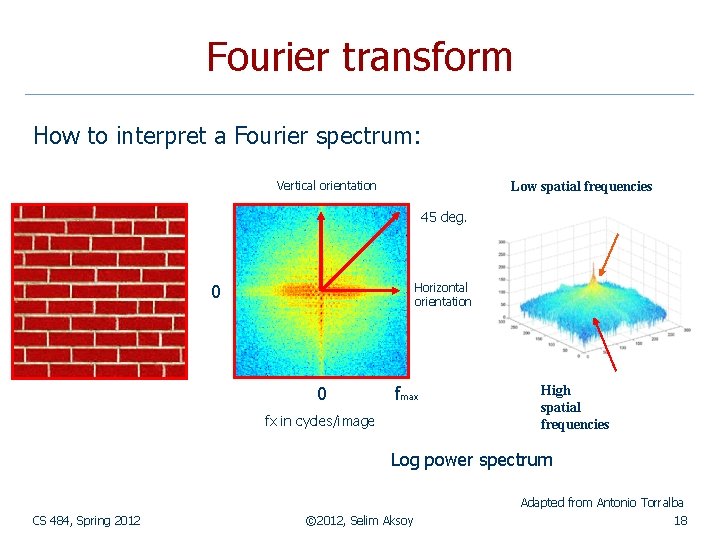
Fourier transform How to interpret a Fourier spectrum: Vertical orientation Low spatial frequencies 45 deg. 0 Horizontal orientation 0 fmax fx in cycles/image High spatial frequencies Log power spectrum Adapted from Antonio Torralba CS 484, Spring 2012 © 2012, Selim Aksoy 18

Fourier transform A 1 B 2 C 3 Adapted from Antonio Torralba CS 484,

Fourier transform A 1 B 2 C 3 Adapted from Antonio Torralba CS 484, Spring 2012 © 2012, Selim Aksoy 19

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Shapiro and

Fourier transform CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Shapiro and Stockman 20

Fourier transform Example building patterns in a satellite image and their Fourier spectrum. CS

Fourier transform Example building patterns in a satellite image and their Fourier spectrum. CS 484, Spring 2012 © 2012, Selim Aksoy 21

Convolution theorem CS 484, Spring 2012 © 2012, Selim Aksoy 22

Convolution theorem CS 484, Spring 2012 © 2012, Selim Aksoy 22

Frequency domain filtering CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Shapiro

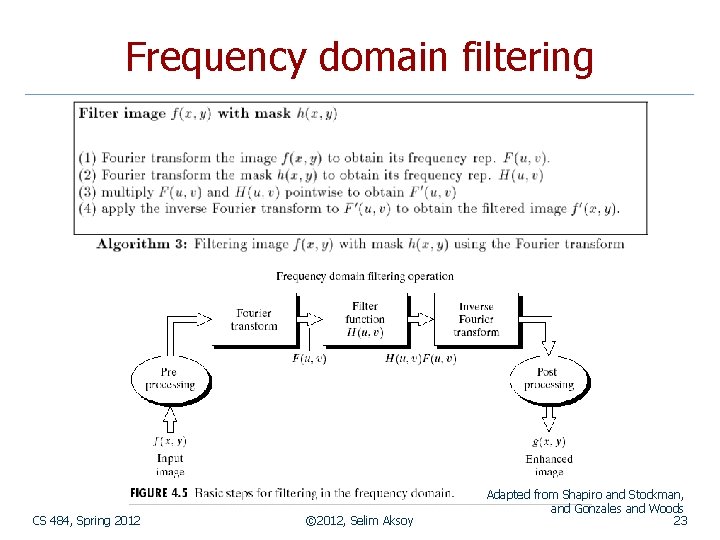
Frequency domain filtering CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Shapiro and Stockman, and Gonzales and Woods 23

Frequency domain filtering n Since the discrete Fourier transform is periodic, padding is needed

Frequency domain filtering n Since the discrete Fourier transform is periodic, padding is needed in the implementation to avoid aliasing (see section 4. 6 in the Gonzales-Woods book for implementation details). CS 484, Spring 2012 © 2012, Selim Aksoy 24

Frequency domain filtering f(x, y) |F(u, v)| h(x, y) |H(u, v)| g(x, y) |G(u,

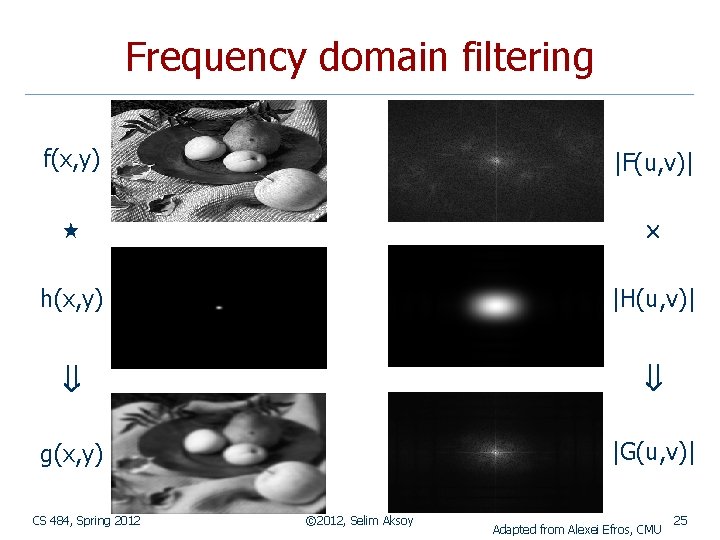
Frequency domain filtering f(x, y) |F(u, v)| h(x, y) |H(u, v)| g(x, y) |G(u, v)| CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Alexei Efros, CMU 25

Smoothing frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 26

Smoothing frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 26

Smoothing frequency domain filters n The blurring and ringing caused by the ideal lowpass

Smoothing frequency domain filters n The blurring and ringing caused by the ideal lowpass filter can be explained using the convolution theorem where the spatial representation of a filter is given below. CS 484, Spring 2012 © 2012, Selim Aksoy 27

Smoothing frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 28

Smoothing frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 28

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 29

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy 29

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and Woods 30

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from

Sharpening frequency domain filters CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and Woods 31

Template matching n n Correlation can also be used for matching. If we want

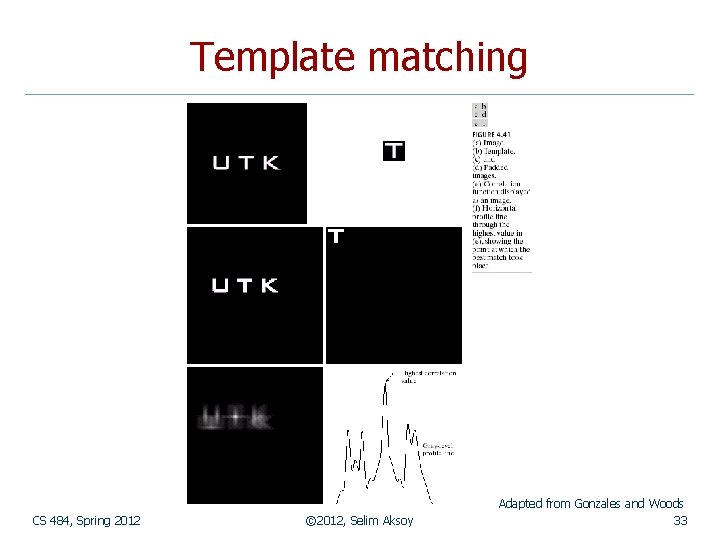
Template matching n n Correlation can also be used for matching. If we want to determine whether an image f contains a particular object, we let h be that object (also called a template) and compute the correlation between f and h. If there is a match, the correlation will be maximum at the location where h finds a correspondence in f. Preprocessing such as scaling and alignment is necessary in most practical applications. CS 484, Spring 2012 © 2012, Selim Aksoy 32

Template matching CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and

Template matching CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and Woods 33

Template matching Face detection using template matching: face templates. CS 484, Spring 2012 ©

Template matching Face detection using template matching: face templates. CS 484, Spring 2012 © 2012, Selim Aksoy 34

Template matching Face detection using template matching: detected faces. CS 484, Spring 2012 ©

Template matching Face detection using template matching: detected faces. CS 484, Spring 2012 © 2012, Selim Aksoy 35

Resizing images How can we generate a half-sized version of a large image? CS

Resizing images How can we generate a half-sized version of a large image? CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Steve Seitz, U of Washington 36

Resizing images 1/8 1/4 Throw away every other row and column to create a

Resizing images 1/8 1/4 Throw away every other row and column to create a 1/2 size image (also called sub-sampling). CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Steve Seitz, U of Washington 37

Resizing images 1/2 CS 484, Spring 2012 1/4 (2 x zoom) 1/8 (4 x

Resizing images 1/2 CS 484, Spring 2012 1/4 (2 x zoom) 1/8 (4 x zoom) Does this look nice? Adapted from Steve Seitz, U of Washington © 2012, Selim Aksoy 38

Resizing images n n We cannot shrink an image by simply taking every k’th

Resizing images n n We cannot shrink an image by simply taking every k’th pixel. Solution: smooth the image, then sub-sample. Gaussian 1/8 Gaussian 1/4 Gaussian 1/2 CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Steve Seitz, U of Washington 39

Resizing images Gaussian 1/2 CS 484, Spring 2012 Gaussian 1/4 (2 x zoom) ©

Resizing images Gaussian 1/2 CS 484, Spring 2012 Gaussian 1/4 (2 x zoom) © 2012, Selim Aksoy Gaussian 1/8 (4 x zoom) Adapted from Steve Seitz, U of Washington 40

Sampling and aliasing CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Steve

Sampling and aliasing CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Steve Seitz, U of Washington 41

Sampling and aliasing n n Errors appear if we do not sample properly. Common

Sampling and aliasing n n Errors appear if we do not sample properly. Common phenomenon: n n High spatial frequency components of the image appear as low spatial frequency components. Examples: n n n Wagon wheels rolling the wrong way in movies. Checkerboards misrepresented in ray tracing. Striped shirts look funny on color television. CS 484, Spring 2012 © 2012, Selim Aksoy 42

Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and

Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Gonzales and Woods 43

Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Michael Black,

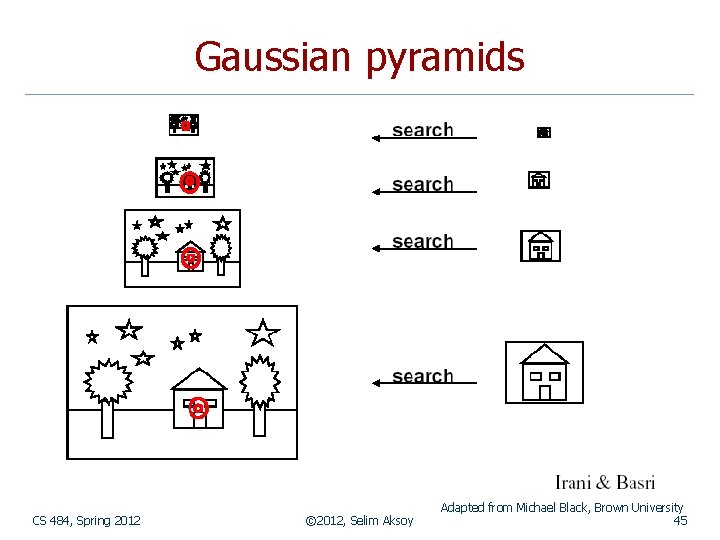
Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Michael Black, Brown University 44

Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Michael Black,

Gaussian pyramids CS 484, Spring 2012 © 2012, Selim Aksoy Adapted from Michael Black, Brown University 45

Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer