Filtering Part II Selim Aksoy Department of Computer

  • Slides: 30
Download presentation
Filtering – Part II Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs. bilkent.

Filtering – Part II Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs. bilkent. edu. tr

Fourier theory n n The Fourier theory shows how most real functions can be

Fourier theory n n The Fourier theory shows how most real functions can be represented in terms of a basis of sinusoids. The building block: n n A sin( ωx + Φ ) Add enough of them to get any signal you want. Adapted from Alexei Efros, CMU CS 484, Fall 2019 © 2019, Selim Aksoy 2

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 3

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 3

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 4

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 4

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 5

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 5

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 6

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 6

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 7

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 7

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 8

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy 8

Fourier transform - matlab A=1; K=10; M=100 ; t=[ones(1, K)*A zeros(1, M-K ; [(

Fourier transform - matlab A=1; K=10; M=100 ; t=[ones(1, K)*A zeros(1, M-K ; [( subplot(3, 1, 1); bar(t); ylim([0 2*A([ subplot(3, 1, 2); bar(abs(fftshift(fft(t)))); ylim([0 A*K+1]) % Matlab uses DFT formulation without normalization by M. subplot(3, 1, 3); bar(real(fftshift(fft(t)))); ylim([-A*K+1]) CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Gonzales and Woods 9

Fourier transform To get some sense of what basis elements look like, we plot

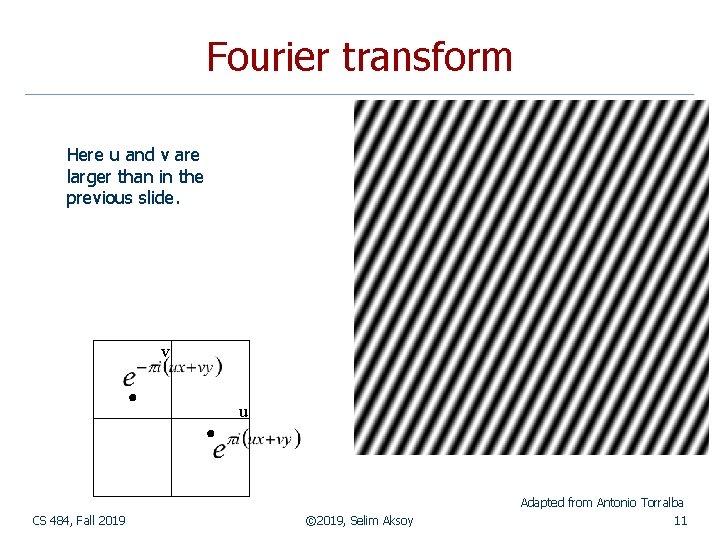
Fourier transform To get some sense of what basis elements look like, we plot a basis element --- or rather, its real part --as a function of x, y for some fixed u, v. We get a function that is constant when (ux+vy) is constant. The magnitude of the vector (u, v) gives a frequency, and its direction gives an orientation. The function is a sinusoid with this frequency along the direction, and constant perpendicular to the direction. v u Adapted from Antonio Torralba CS 484, Fall 2019 © 2019, Selim Aksoy 10

Fourier transform Here u and v are larger than in the previous slide. v

Fourier transform Here u and v are larger than in the previous slide. v u Adapted from Antonio Torralba CS 484, Fall 2019 © 2019, Selim Aksoy 11

Fourier transform And larger still. . . v u Adapted from Antonio Torralba CS

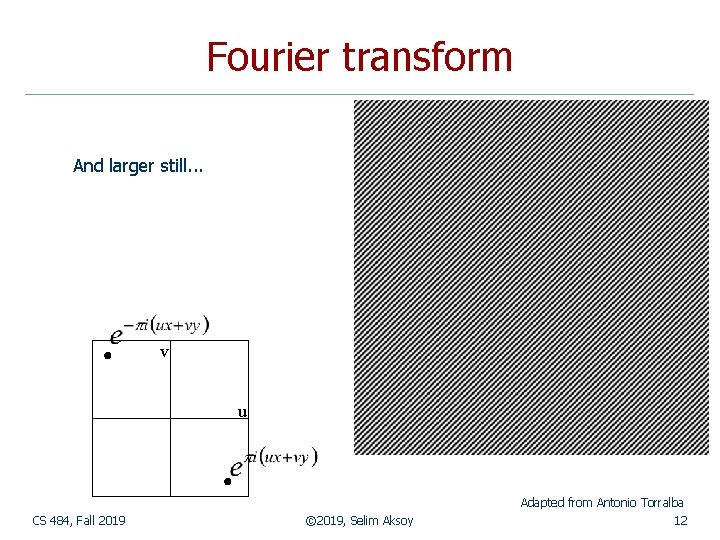
Fourier transform And larger still. . . v u Adapted from Antonio Torralba CS 484, Fall 2019 © 2019, Selim Aksoy 12

Fourier transform How to interpret a Fourier spectrum: Vertical orientation Low spatial frequencies 45

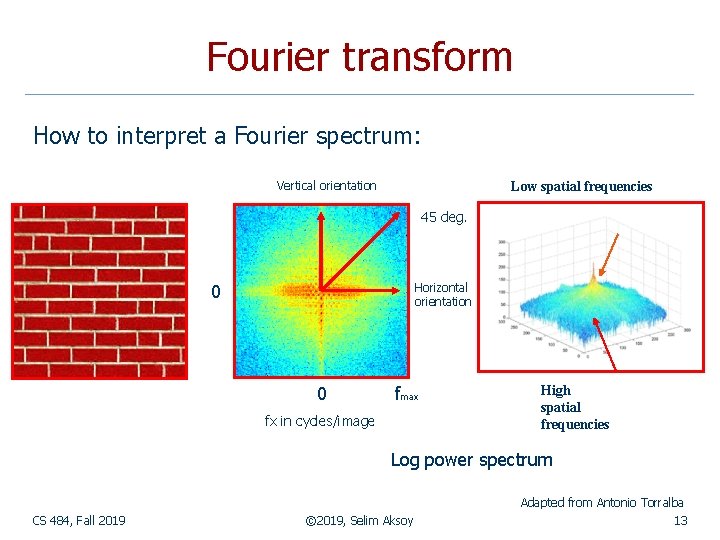
Fourier transform How to interpret a Fourier spectrum: Vertical orientation Low spatial frequencies 45 deg. 0 Horizontal orientation 0 fmax fx in cycles/image High spatial frequencies Log power spectrum Adapted from Antonio Torralba CS 484, Fall 2019 © 2019, Selim Aksoy 13

Fourier transform A 1 B 2 C 3 Adapted from Antonio Torralba CS 484,

Fourier transform A 1 B 2 C 3 Adapted from Antonio Torralba CS 484, Fall 2019 © 2019, Selim Aksoy 14

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Shapiro and

Fourier transform CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Shapiro and Stockman 15

Convolution theorem CS 484, Fall 2019 © 2019, Selim Aksoy 16

Convolution theorem CS 484, Fall 2019 © 2019, Selim Aksoy 16

Frequency domain filtering CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Shapiro

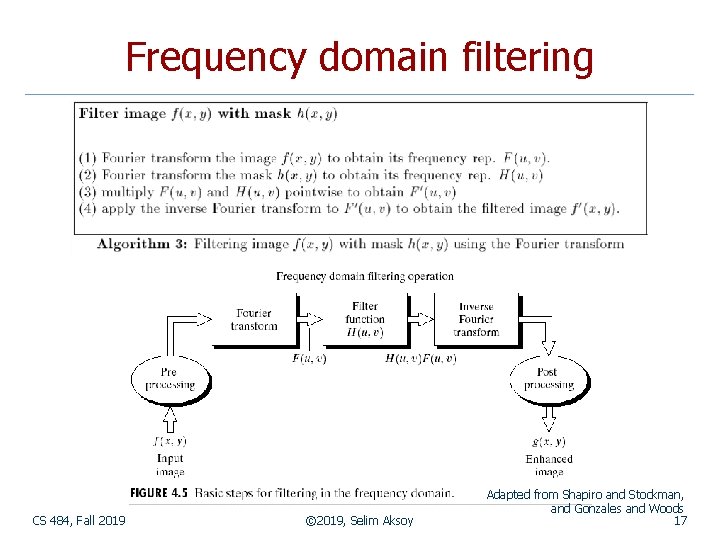
Frequency domain filtering CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Shapiro and Stockman, and Gonzales and Woods 17

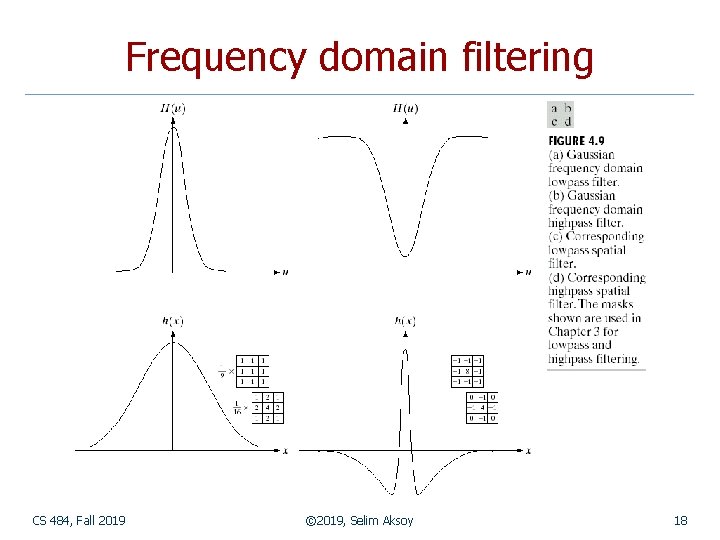
Frequency domain filtering CS 484, Fall 2019 © 2019, Selim Aksoy 18

Frequency domain filtering CS 484, Fall 2019 © 2019, Selim Aksoy 18

Frequency domain filtering f(x, y) |F(u, v)| h(x, y) |H(u, v)| g(x, y) |G(u,

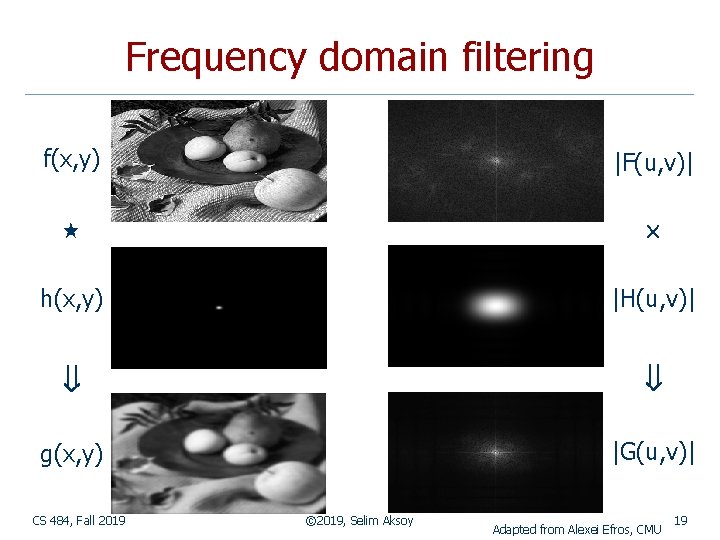
Frequency domain filtering f(x, y) |F(u, v)| h(x, y) |H(u, v)| g(x, y) |G(u, v)| CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Alexei Efros, CMU 19

Template matching n n Correlation can also be used for matching. If we want

Template matching n n Correlation can also be used for matching. If we want to determine whether an image f contains a particular object, we let h be that object (also called a template) and compute the correlation between f and h. If there is a match, the correlation will be maximum at the location where h finds a correspondence in f. Preprocessing such as scaling and alignment is necessary in most practical applications. CS 484, Fall 2019 © 2019, Selim Aksoy 20

Template matching Face detection using template matching: detected faces. CS 484, Fall 2019 ©

Template matching Face detection using template matching: detected faces. CS 484, Fall 2019 © 2019, Selim Aksoy 21

Resizing images How can we generate a half-sized version of a large image? CS

Resizing images How can we generate a half-sized version of a large image? CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Steve Seitz, U of Washington 22

Resizing images 1/8 1/4 Throw away every other row and column to create a

Resizing images 1/8 1/4 Throw away every other row and column to create a 1/2 size image (also called sub-sampling). CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Steve Seitz, U of Washington 23

Resizing images 1/2 CS 484, Fall 2019 1/4 (2 x zoom) 1/8 (4 x

Resizing images 1/2 CS 484, Fall 2019 1/4 (2 x zoom) 1/8 (4 x zoom) Does this look nice? Adapted from Steve Seitz, U of Washington © 2019, Selim Aksoy 24

Resizing images n n We cannot shrink an image by simply taking every k’th

Resizing images n n We cannot shrink an image by simply taking every k’th pixel. Solution: smooth the image, then sub-sample. Gaussian 1/8 Gaussian 1/4 Gaussian 1/2 CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Steve Seitz, U of Washington 25

Resizing images Gaussian 1/2 CS 484, Fall 2019 Gaussian 1/4 (2 x zoom) ©

Resizing images Gaussian 1/2 CS 484, Fall 2019 Gaussian 1/4 (2 x zoom) © 2019, Selim Aksoy Gaussian 1/8 (4 x zoom) Adapted from Steve Seitz, U of Washington 26

Sampling and aliasing n n Errors appear if we do not sample properly. Common

Sampling and aliasing n n Errors appear if we do not sample properly. Common phenomenon: n n High spatial frequency components of the image appear as low spatial frequency components. Examples: n n n Wagon wheels rolling the wrong way in movies. Checkerboards misrepresented in ray tracing. Striped shirts look funny on color television. CS 484, Fall 2019 © 2019, Selim Aksoy 27

Sampling and aliasing CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Ali

Sampling and aliasing CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Ali Farhadi 28

Gaussian pyramids CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Gonzales and

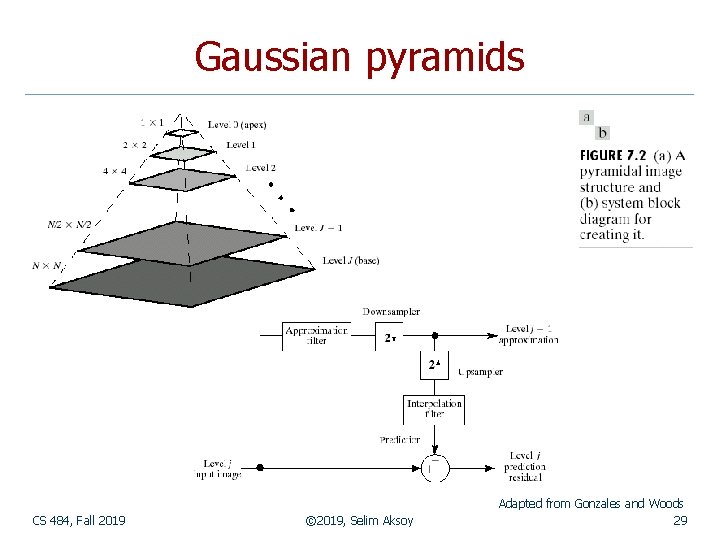
Gaussian pyramids CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Gonzales and Woods 29

Gaussian pyramids CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Michael Black,

Gaussian pyramids CS 484, Fall 2019 © 2019, Selim Aksoy Adapted from Michael Black, Brown University 30

Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part II Selim Aksoy Department of ComputerFiltering Part II Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Filtering Part I Selim Aksoy Department of ComputerFiltering Part I Selim Aksoy Department of Computer
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of
Linear Filtering Part I Selim Aksoy Department ofLinear Filtering Part I Selim Aksoy Department of
Linear Filtering Part II Selim Aksoy Department ofLinear Filtering Part II Selim Aksoy Department of