Lecture 4 Addition and free vector spaces of

Lecture 4: Addition (and free vector spaces) of a series of preparatory lectures for the Fall 2013 online course MATH: 7450 (22 M: 305) Topics in Topology: Scientific and Engineering Applications of Algebraic Topology Target Audience: Anyone interested in topological data analysis including graduate students, faculty, industrial researchers in bioinformatics, biology, computer science, cosmology, engineering, imaging, mathematics, neurology, physics, statistics, etc. Isabel K. Darcy Mathematics Department/Applied Mathematical & Computational Sciences University of Iowa http: //www. math. uiowa. edu/~idarcy/Applied. Topology. html

A free abelian group generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni are integers. Z = The set of integers = { …, -2, -1, 0, 1, 2, …} = the set of all whole numbers (positive, negative, 0) Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk

A free abelian group generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni are integers. Example: Z[x , x ] 4 ix + 2 I x – 2 i -3 x k + n iii Z = The set of integers = { …, -2, -1, 0, 1, 2, …}

A free abelian group generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni are integers. Z = The set of integers = { …, -2, -1, 0, 1, 2, …} = the set of all whole numbers (positive, negative, 0) Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk

A free vector space over the field F generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni in F. Examples of a field: R = set of real numbers Q = set of rational numbers Z 2 = {0, 1} Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk

A free vector space over the field F generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni in F. Examples of a field: R = set of real numbers: πx + √ 2 y + 3 z is in R[x, y, z] Q = set of rational numbers (i. e. fractions): (½)x + 4 y is in Q[x, y] Z 2 = {0, 1}: 0 x + 1 y + 1 w + 0 z is in Z 2[x, y, z, w]

Group Closure Associative Identity Inverses x, y in G implies x + y is in G (x + y) + z = x + (y + z) 0+x=x=x+0 x + (-x) = 0 = (-x) + x Examples of a group under addition: R = set of real numbers Q = set of rational numbers. Z = set of integers. Z 2 = {0, 1}

Group Closure Associative Identity Inverses Abelian Group Closure Associative Identity Inverses Commutative x, y in G implies x + y is in G (x + y) + z = x + (y + z) 0+x=x=x+0 x + (-x) = 0 = (-x) + x x+y=y+x

Abelian Group Closure Associative Identity Inverses Commutative x, y in G implies x + y is in G (x + y) + z = x + (y + z) 0+x=x=x+0 x + (-x) = 0 = (-x) + x x+y=y+x Examples of an abelian group under addition: R = set of real numbers Q = set of rational numbers. Z = set of integers. Z 2 = {0, 1}

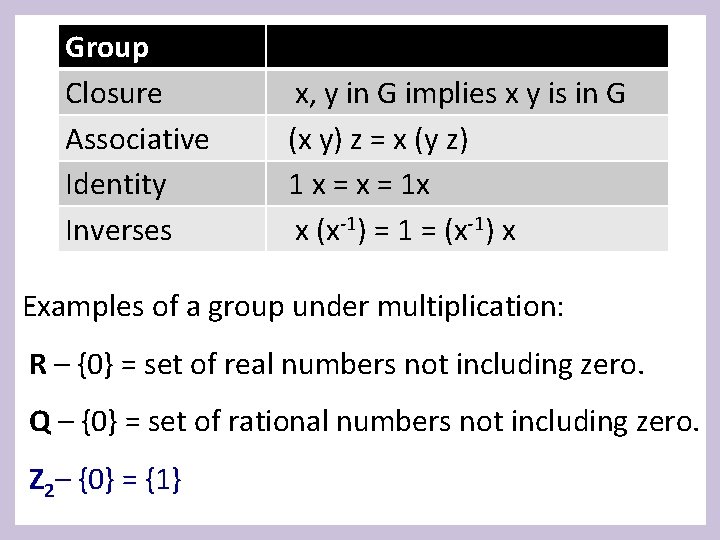
Group Closure Associative Identity Inverses x, y in G implies x y is in G (x y) z = x (y z) 1 x = 1 x x (x-1) = 1 = (x-1) x Examples of a group under multiplication: R – {0} = set of real numbers not including zero. Q – {0} = set of rational numbers not including zero. Z 2– {0} = {1}

Group Closure Associative Identity Inverses x, y in G implies x y is in G (x y) z = x (y z) 1 x = 1 x x (x-1) = 1 = (x-1) x Note that Z – {0} is not a group under multiplication.

F is a field if (1) F is an abelian group under addition (2) F – {0} is an abelian group under multiplication (3) multiplication distributes across addition. Field Closure Associative Identity Inverses Commutative Distributive Addition x, y in G x+ y in G (x + y) + z = x + (y + z) 0+x=x=x+0 x + (-x) = 0 = (-x) + x x+y=y+x x(y+z) = Multiplication closure (x y) z = x (y z) 1 x = 1 x x (x-1) = 1 = (x-1) x (x y) z = x (y z) xy+xz Examples of a field: R = set of real numbers Q = set of rational numbers Z 2 = {0, 1}

A free vector space over the field F generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni in F. Examples of a field: R = set of real numbers Q = set of rational numbers Z 2 = {0, 1} Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk

A free abelian group generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni are integers. Z = The set of integers = { …, -2, -1, 0, 1, 2, …} = the set of all whole numbers (positive, negative, 0) Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk

A free vector space over the field Z 2 generated by the elements x 1, x 2, …, xk consists of all elements of the form n 1 x 1 + n 2 x 2 + … + n k xk where ni in Z 2. Example: Z 2[x 1, x 2] = {0, x 1, x 2, x 1 + x 2} 4 x 1 + 2 x 2 = 0 x 1 + 0 x 2 = 0 mod 2 1 x 1 + 0 x 2 = x 1 mod 2 0 x 1 + 1 x 2 = x 2 mod 2 kx 1 + nx 2 mod 2 Z 2 = The set of integers mod 2 = {0, 1}

Addition: (n 1 x 1 + n 2 x 2 + … + nkxk) + (m 1 x 1 + m 2 x 2 + … + mkxk) = (n 1 + m 1) x 1 + (n 2 + m 2)x 2 + … + (nk + mk)xk Example: Z 2[x 1, x 2] = {0, x 1, x 2, x 1 + x 2} 1 x 1 + 1 x 1 = 2 x 1 = 0 mod 2 (x 1 + x 2) + (x 1 + 0 x 2) = 2 x 1 + x 2 = x 2 mod 2 (1 x 1 + 0 x 2) + (0 x 1 + 1 x 2) = x 1 + x 2 mod 2

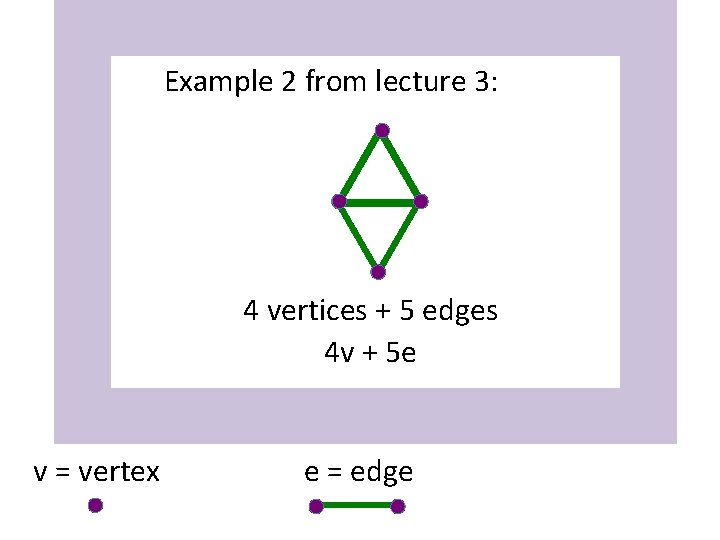
Example 2 from lecture 3: 4 vertices + 5 edges 4 v + 5 e v = vertex e = edge

Example 2 from lecture 3: 0 vertices + 1 edges mod 2 0 v + 1 e = e mod 2 v = vertex e = edge

Example 2 from lecture 3: 0 vertices + 1 edges mod 2 0 v + 1 e = e mod 2 v = vertex e = edge

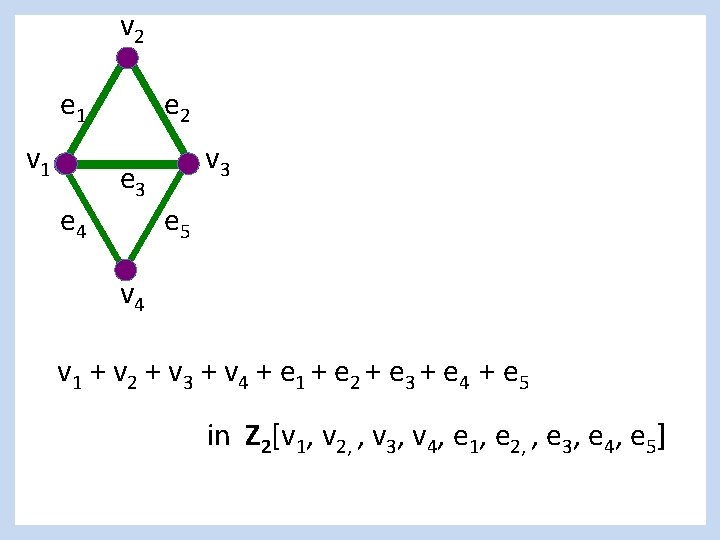
v 2 e 1 v 1 e 4 e 2 e 3 v 3 e 5 v 4 v 1 + v 2 + v 3 + v 4 + e 1 + e 2 + e 3 + e 4 + e 5 in Z 2[v 1, v 2, , v 3, v 4, e 1, e 2, , e 3, e 4, e 5]

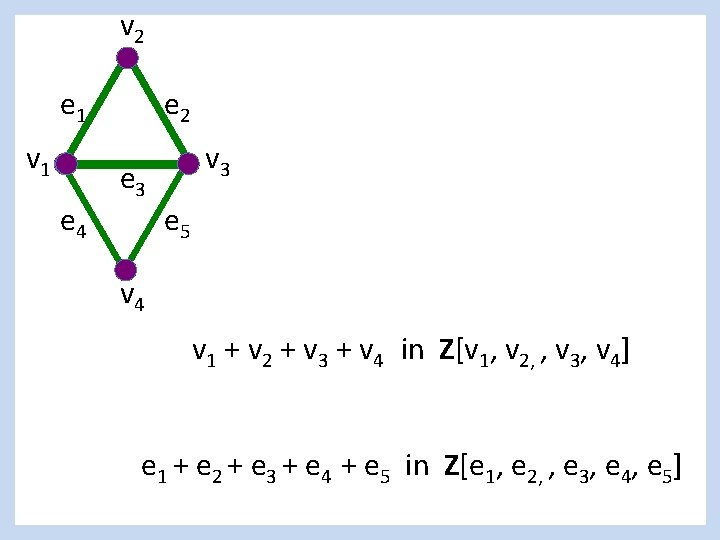
v 2 e 1 v 1 e 4 e 2 e 3 v 3 e 5 v 4 v 1 + v 2 + v 3 + v 4 in Z[v 1, v 2, , v 3, v 4] e 1 + e 2 + e 3 + e 4 + e 5 in Z[e 1, e 2, , e 3, e 4, e 5]

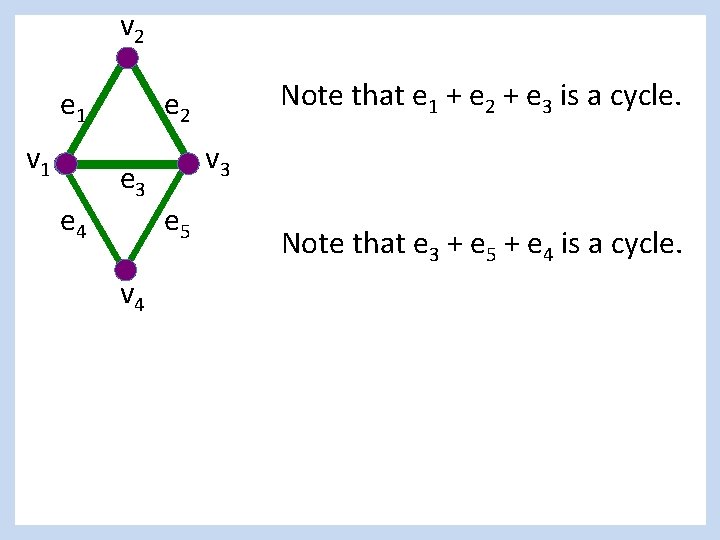
v 2 e 1 v 1 e 4 Note that e 1 + e 2 + e 3 is a cycle. e 2 e 3 v 4 v 3 e 5 Note that e 3 + e 5 + e 4 is a cycle.

In Z[e 1, e 2, e 3, e 4, e 5] Objects: oriented edges e ei –e But in Z 2, 1 = -1. Thus e = – e

In Z[e 1, e 2, e 3, e 4, e 5] Objects: oriented edges e ei –e But in Z 2, 1 = -1. Thus e = – e e = –e

In Z[e 1, e 2, e 3, e 4, e 5] Objects: oriented edges e ei –e But in Z 2, 1 = -1. Thus e = – e e = –e

In Z[e 1, e 2, e 3, e 4, e 5] Objects: oriented edges ei ei – ei In Z 2[e 1, e 2, e 3, e 4, e 5] Objects: edges ei

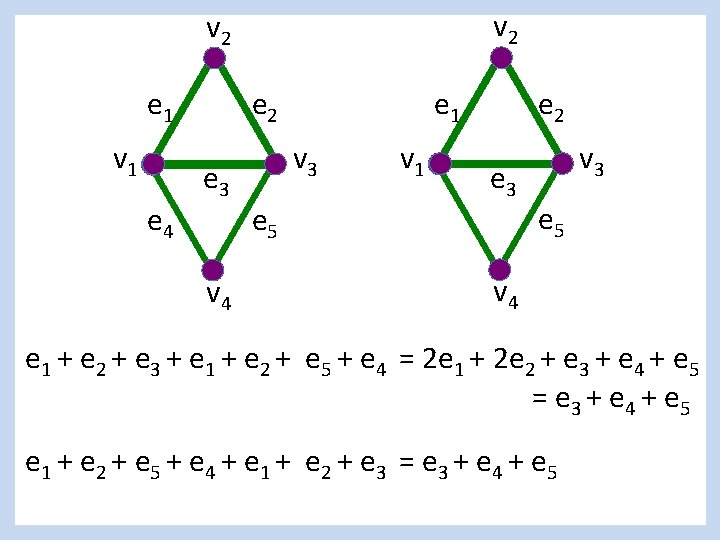
In Z[e 1, e 2, e 3, e 4, e 5] e 1 e 4 e 3 e 2 e 1 e 2 e 5 e 4 e 5 (e 1 + e 2 + e 3) + (–e 3 + e 5 + e 4) = e 1 + e 2 + e 5 + e 4

In Z 2[e 1, e 2, e 3, e 4, e 5] e 1 e 4 e 3 e 2 e 1 e 2 e 5 e 4 e 5 (e 1 + e 2 + e 3) + (e 3 + e 5 + e 4) = e 1 + e 2 + 2 e 3 + e 5 + e 4 = e 1 + e 2 + e 5 + e 4 .

v 2 e 1 v 1 e 4 e 1 e 2 e 3 v 4 v 3 e 5 v 1 e 2 e 3 v 3 e 5 v 4 e 1 + e 2 + e 3 + e 1 + e 2 + e 5 + e 4 = 2 e 1 + 2 e 2 + e 3 + e 4 + e 5 = e 3 + e 4 + e 5 e 1 + e 2 + e 5 + e 4 + e 1 + e 2 + e 3 = e 3 + e 4 + e 5

In Z[e 1, e 2, e 3, e 4, e 5] v 2 e 1 v 1 e 4 The boundary of e 1 = v 2 – v 1 e 2 e 3 v 4 v 3 e 5

v 2 e 1 v 1 e 4 In Z 2[e 1, e 2, e 3, e 4, e 5] The boundary of e 1 = v 2 + v 1 e 2 e 3 v 4 v 3 e 5

v 2 e 1 v 1 e 4 In Z 2[e 1, e 2, e 3, e 4, e 5] The boundary of e 1 = v 2 + v 1 e 2 e 3 v 3 e 5 The boundary of e 2 = v 3 + v 2 The boundary of e 3 = v 1 + v 3 v 4 The boundary of e 1 + e 2 + e 3 = v 2 + v 1 + v 3 + v 2 + v 1 + v 3 = 2 v 1 + 2 v 2 + 2 v 3 = 0

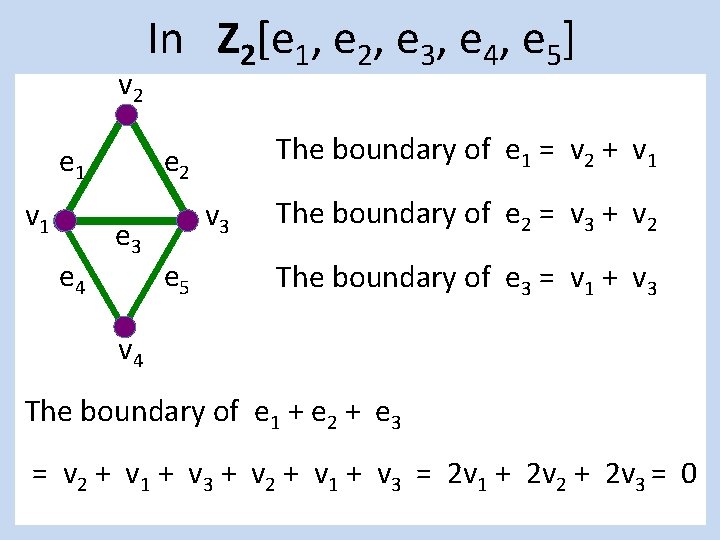
In Z[f] Add an oriented face v 2 e 1 v 1 e 4 v 2 e 3 v 4 e 1 v 3 e 5 v 1 e 4 e 2 e 3 v 4 v 3 e 5

Add an oriented face v 2 e 1 v 1 e 4 v 2 e 3 v 4 e 1 v 3 e 5 v 1 e 4 e 2 e 3 v 4 But with Z 2 coefficients +1 = -1 so f = -f. v 3 e 5

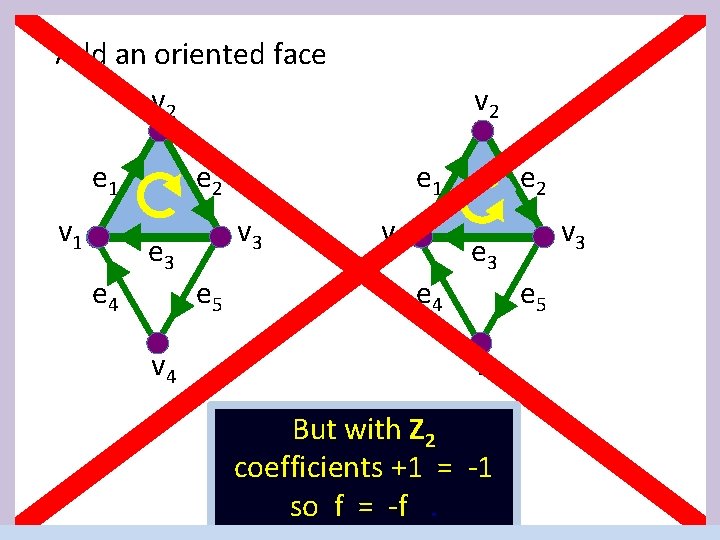
In Z 2[f] Add a face v 2 e 1 v 1 e 4 e 2 e 3 v 4 v 3 e 5

Building blocks for a simplicial complex using Z 2 coefficients 0 -simplex = vertex = v 1 -simplex = edge = {v 1, v 2} v 1 e v 2 Note that the boundary of this edge is v 2 + v 1 2 -simplex = face = {v 1, v 2, v 3} v 2 Note that the boundary of this face is the cycle e 1 e 2 e 1 + e 2 + e 3 v 1 v 3 e 3 = {v 1, v 2} + {v 2, v 3} + {v 1, v 3}

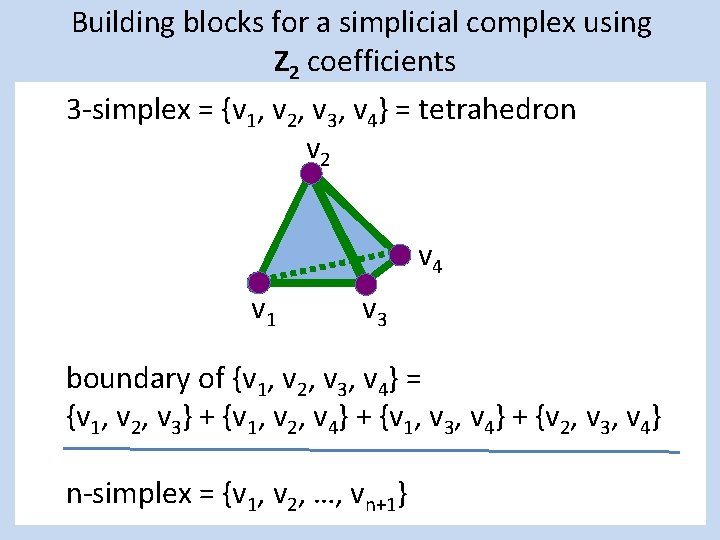
Building blocks for a simplicial complex using Z 2 coefficients 3 -simplex = {v 1, v 2, v 3, v 4} = tetrahedron v 2 v 4 v 1 v 3 boundary of {v 1, v 2, v 3, v 4} = {v 1, v 2, v 3} + {v 1, v 2, v 4} + {v 1, v 3, v 4} + {v 2, v 3, v 4} n-simplex = {v 1, v 2, …, vn+1}