Lecture 10 6 GRAPHS Discrete Mathematics Dr Ing

Lecture 10 6. GRAPHS Discrete Mathematics Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

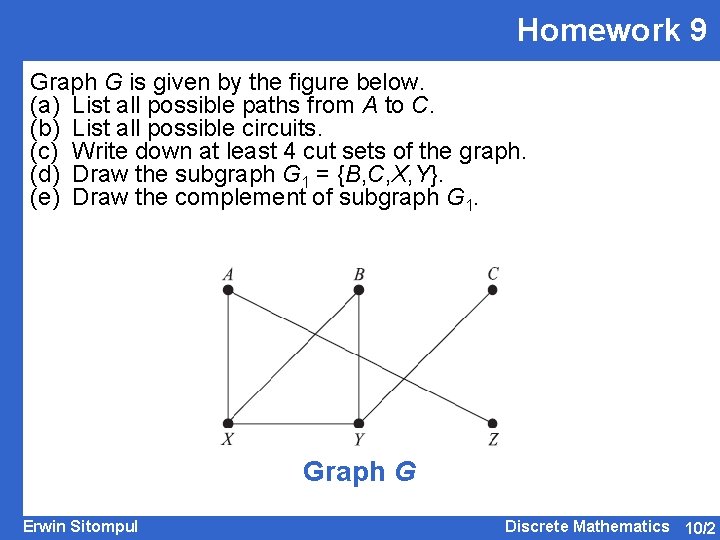
Homework 9 Graph G is given by the figure below. (a) List all possible paths from A to C. (b) List all possible circuits. (c) Write down at least 4 cut sets of the graph. (d) Draw the subgraph G 1 = {B, C, X, Y}. (e) Draw the complement of subgraph G 1. Graph G Erwin Sitompul Discrete Mathematics 10/2

Solution of Homework 9 (a) All possible paths from A to C. (A, X, Y, C) and (A, X, B, Y, C) (b) All possible circuits. (B, X, Y, B) (c) At least 4 cut sets of the graph. {(A, Z)}, {(A, X)}, {(C, Y)}, {(A, Z), (A, X)}, {(B, X), (B, Y)}, {(B, X), (X, Y)} Graph G Erwin Sitompul Discrete Mathematics 10/3

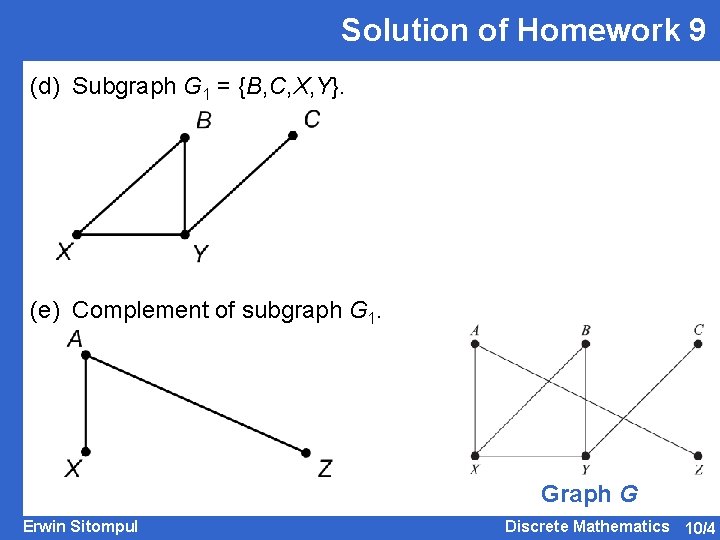
Solution of Homework 9 (d) Subgraph G 1 = {B, C, X, Y}. (e) Complement of subgraph G 1. Graph G Erwin Sitompul Discrete Mathematics 10/4

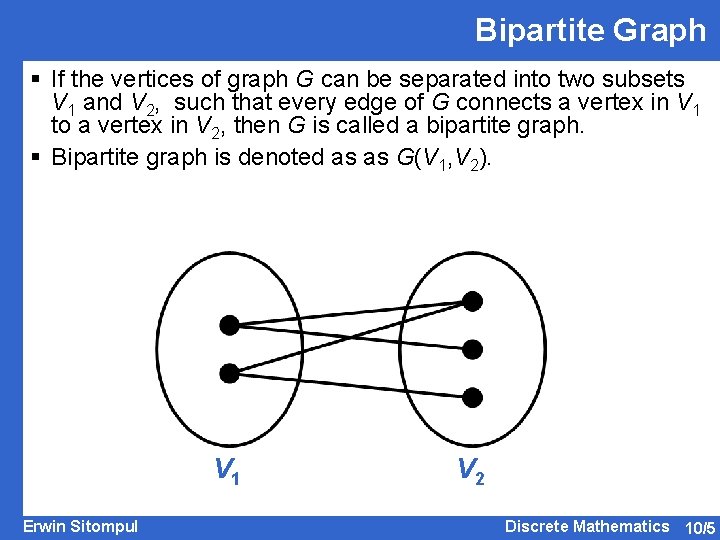
Bipartite Graph § If the vertices of graph G can be separated into two subsets V 1 and V 2, such that every edge of G connects a vertex in V 1 to a vertex in V 2, then G is called a bipartite graph. § Bipartite graph is denoted as as G(V 1, V 2). V 1 Erwin Sitompul V 2 Discrete Mathematics 10/5

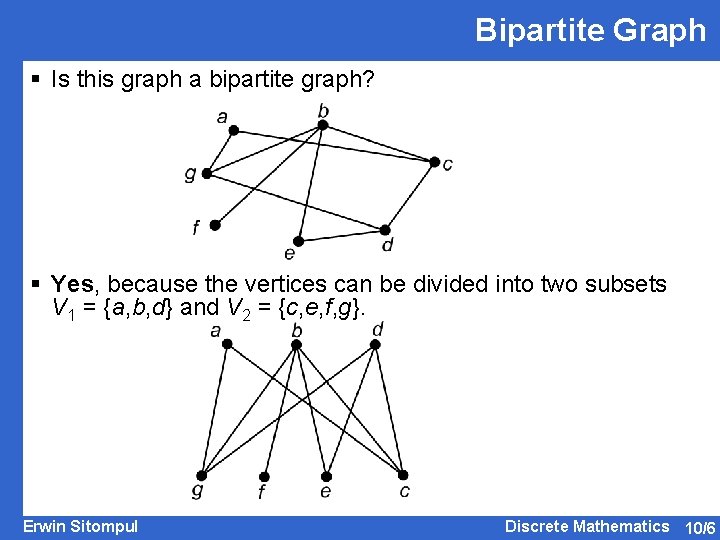
Bipartite Graph § Is this graph a bipartite graph? § Yes, because the vertices can be divided into two subsets V 1 = {a, b, d} and V 2 = {c, e, f, g}. Erwin Sitompul Discrete Mathematics 10/6

Isomorphic Graph § Graphs that are actually identical but geometrically different are called isomorphic. § Two graphs G 1 and G 2 are isomorphic if there is a one-to-one correspondence between vertices of the two graphs that preserves the adjacency relationship. § In other words, suppose the edge e is incident to vertex u and vertex v in G 1, then the corresponding edge e’ must be incident to vertex u’ and vertex v’ in G 2. § Two isomorphic graphs are identical graphs, different only in the naming of the vertices and edges or the geometrical representation only. Erwin Sitompul Discrete Mathematics 10/7

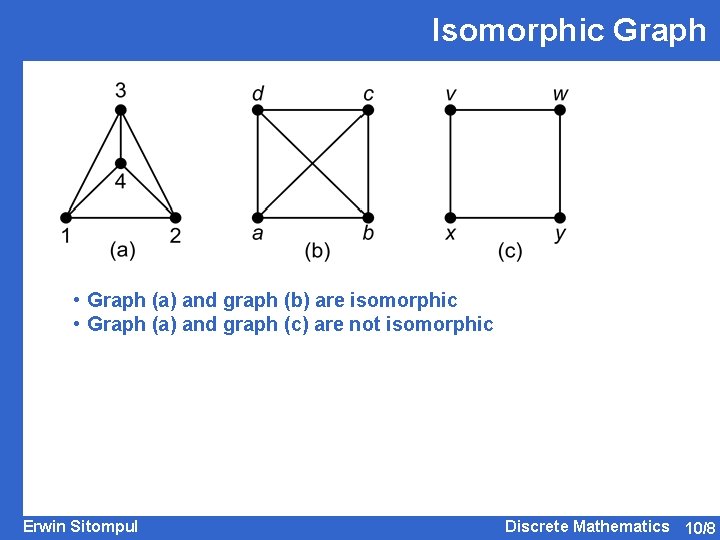
Isomorphic Graph • Graph (a) and graph (b) are isomorphic • Graph (a) and graph (c) are not isomorphic Erwin Sitompul Discrete Mathematics 10/8

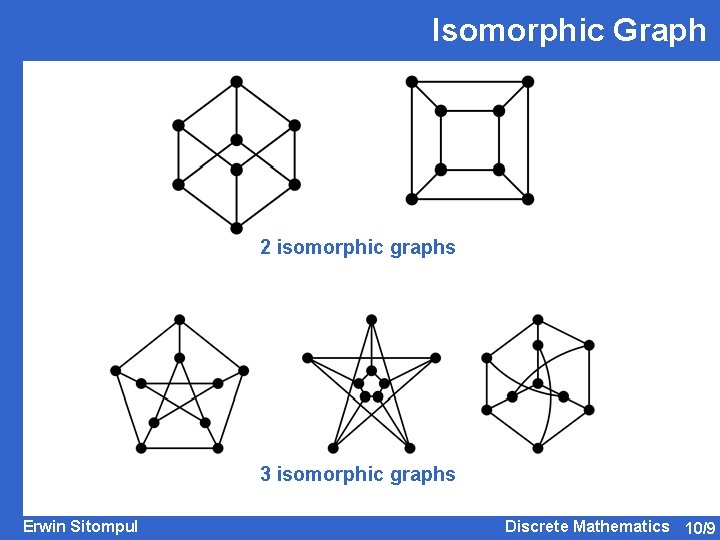
Isomorphic Graph 2 isomorphic graphs 3 isomorphic graphs Erwin Sitompul Discrete Mathematics 10/9

Isomorphic Graph § From the definition of isomorphic graphs, it can be concluded that if two graphs are isomorphic, then both of them: 1. Have the same number of vertices. 2. Have the same number of edges. 3. Have the same number of vertices of each degree. § The 3 conditions listed above are necessary conditions, but not sufficient conditions. § Further visual inspection is required, as can be seen from the example below. The 3 conditions are met but both graphs are not isomorphic. Erwin Sitompul Discrete Mathematics 10/10

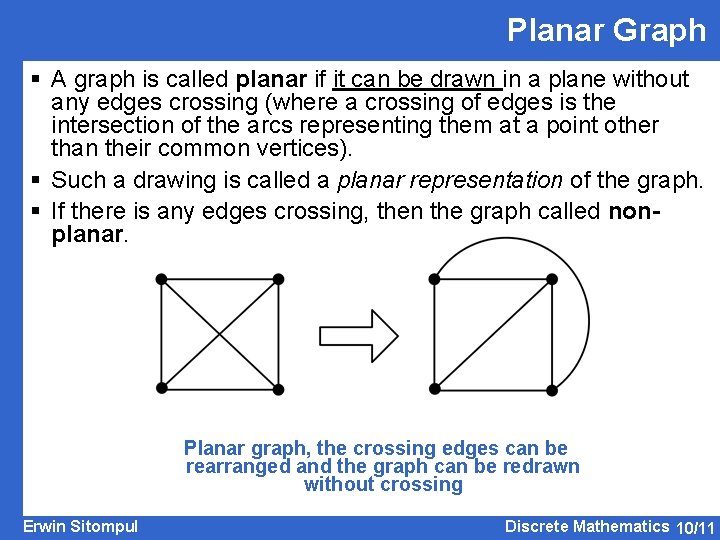
Planar Graph § A graph is called planar if it can be drawn in a plane without any edges crossing (where a crossing of edges is the intersection of the arcs representing them at a point other than their common vertices). § Such a drawing is called a planar representation of the graph. § If there is any edges crossing, then the graph called nonplanar. Planar graph, the crossing edges can be rearranged and the graph can be redrawn without crossing Erwin Sitompul Discrete Mathematics 10/11

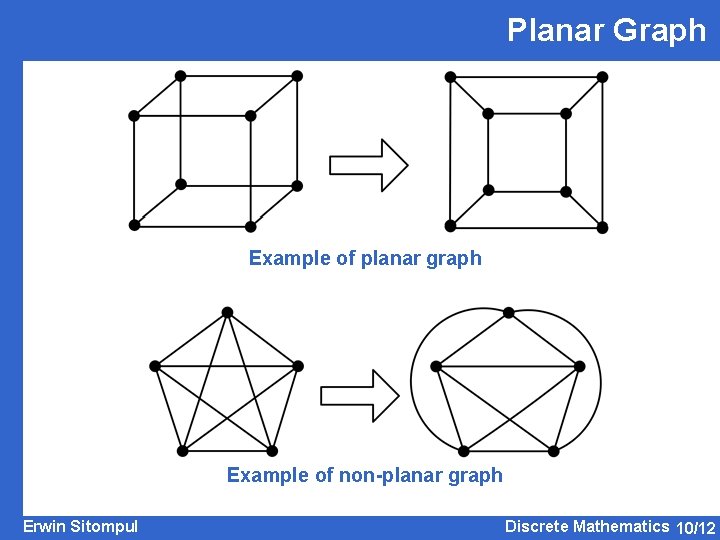
Planar Graph Example of planar graph Example of non-planar graph Erwin Sitompul Discrete Mathematics 10/12

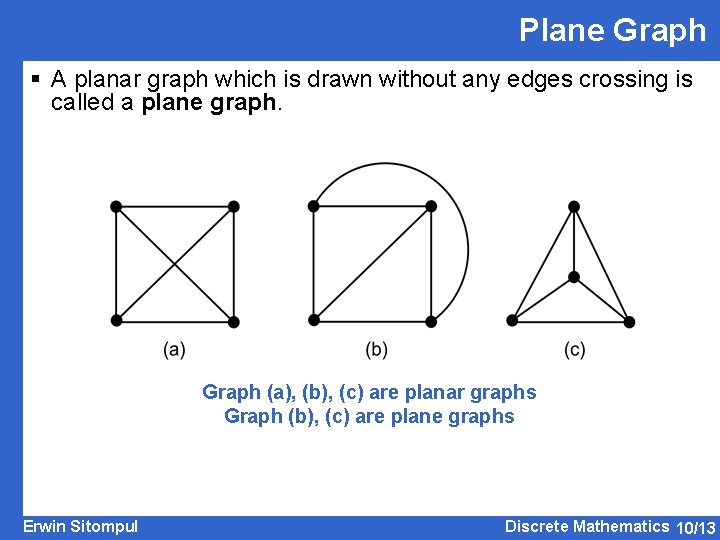
Plane Graph § A planar graph which is drawn without any edges crossing is called a plane graph. Graph (a), (b), (c) are planar graphs Graph (b), (c) are plane graphs Erwin Sitompul Discrete Mathematics 10/13

Euler Path and Euler Circuit § An Euler path in a graph is a path that contains every edge of the graph exactly once. § An Euler circuit in a graph is a circuit that contains every edge of a graph exactly once. § A graph that contains Euler path is also called semi-Eulerian graph. § A graph that contains Euler circuit is also called Eulerian graph. Erwin Sitompul Discrete Mathematics 10/14

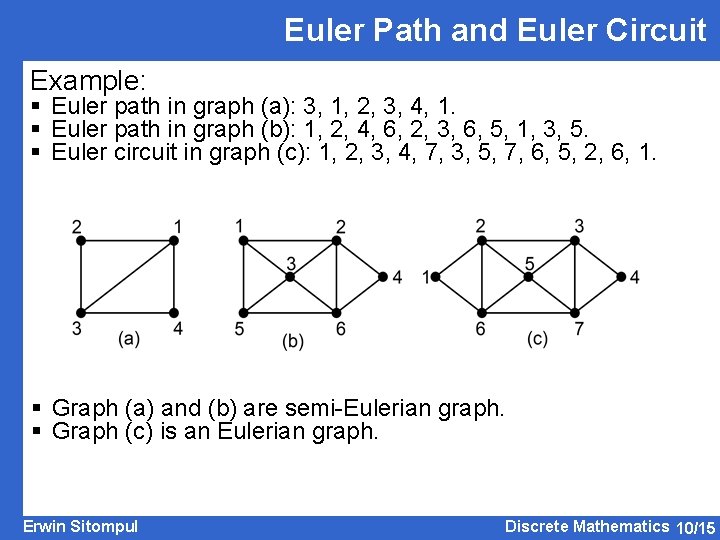
Euler Path and Euler Circuit Example: § Euler path in graph (a): 3, 1, 2, 3, 4, 1. § Euler path in graph (b): 1, 2, 4, 6, 2, 3, 6, 5, 1, 3, 5. § Euler circuit in graph (c): 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1. § Graph (a) and (b) are semi-Eulerian graph. § Graph (c) is an Eulerian graph. Erwin Sitompul Discrete Mathematics 10/15

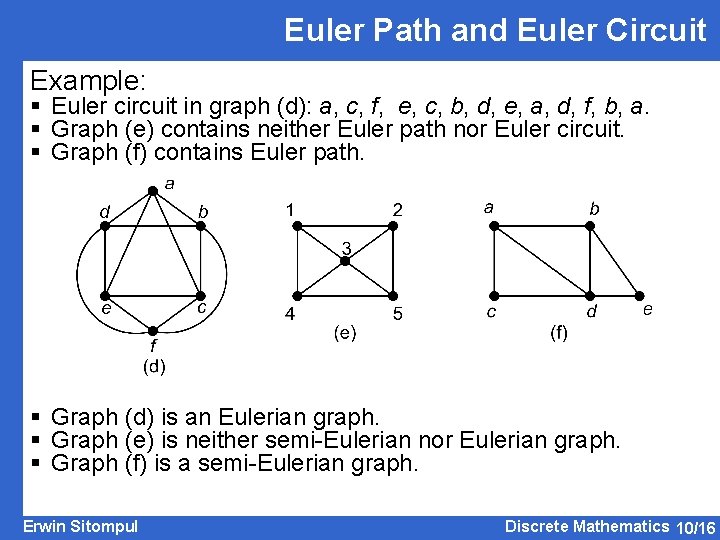
Euler Path and Euler Circuit Example: § Euler circuit in graph (d): a, c, f, e, c, b, d, e, a, d, f, b, a. § Graph (e) contains neither Euler path nor Euler circuit. § Graph (f) contains Euler path. § Graph (d) is an Eulerian graph. § Graph (e) is neither semi-Eulerian nor Eulerian graph. § Graph (f) is a semi-Eulerian graph. Erwin Sitompul Discrete Mathematics 10/16

Euler Path and Euler Circuit Theorem: An undirected graph G contains Euler path if and only if it is connected and has two vertices of odd degree or does not have any vertices of odd degree at all. Theorem: An undirected graph G contains Euler circuit if and only if it is connected and each of its vertices has even degree. § In other words: An undirected graph G is an Eulerian graph if and only if the degree of every vertex is even. Erwin Sitompul Discrete Mathematics 10/17

Euler Path and Euler Circuit Theorem: A directed graph G contains Euler path if and only if G is connected and for each vertex, the in-degree and out-degree are the same, except two vertices, where the first vertex’s outdegree is one greater than the in-degree and the second vertex’s in-degree is one greater than the out-degree. Theorem: A directed graph G contains Euler circuit if and only if G is connected and for each vertex, the in-degree and out-degree are the same. Erwin Sitompul Discrete Mathematics 10/18

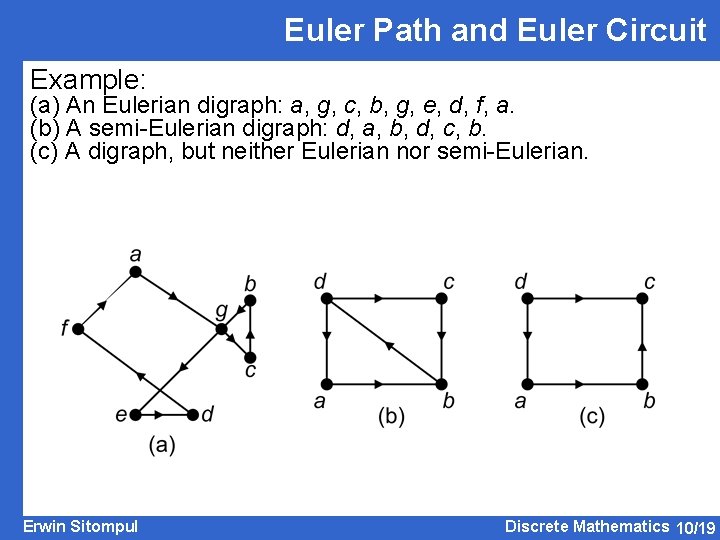
Euler Path and Euler Circuit Example: (a) An Eulerian digraph: a, g, c, b, g, e, d, f, a. (b) A semi-Eulerian digraph: d, a, b, d, c, b. (c) A digraph, but neither Eulerian nor semi-Eulerian. Erwin Sitompul Discrete Mathematics 10/19

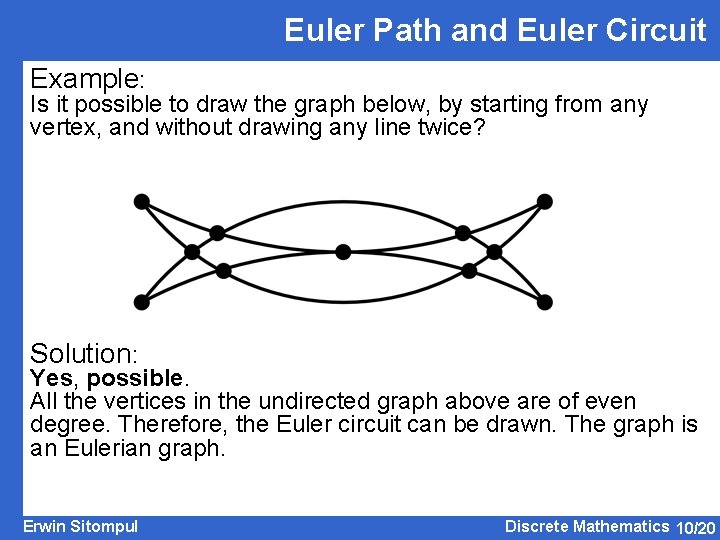
Euler Path and Euler Circuit Example: Is it possible to draw the graph below, by starting from any vertex, and without drawing any line twice? Solution: Yes, possible. All the vertices in the undirected graph above are of even degree. Therefore, the Euler circuit can be drawn. The graph is an Eulerian graph. Erwin Sitompul Discrete Mathematics 10/20

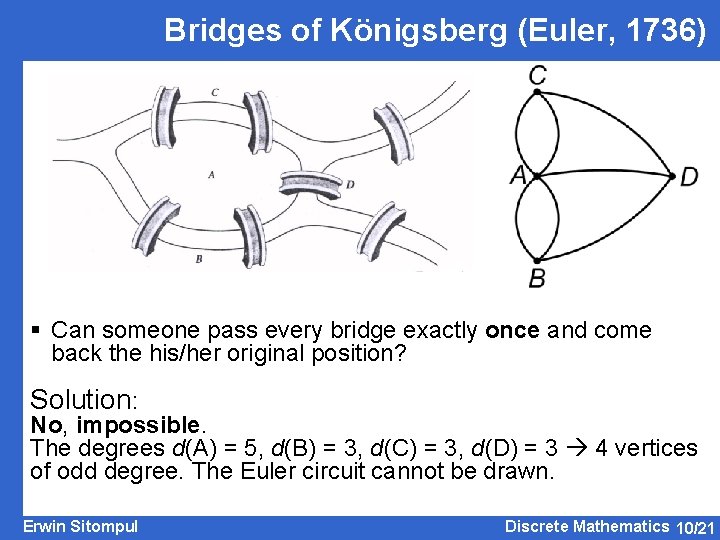
Bridges of Königsberg (Euler, 1736) § Can someone pass every bridge exactly once and come back the his/her original position? Solution: No, impossible. The degrees d(A) = 5, d(B) = 3, d(C) = 3, d(D) = 3 4 vertices of odd degree. The Euler circuit cannot be drawn. Erwin Sitompul Discrete Mathematics 10/21

Hamilton Path and Hamilton Circuit § A Hamilton path in a graph is a path that passes every vertex of the graph exactly once. § A Hamilton circuit in a graph is a circuit that passes every vertex of the graph exactly once, except one vertex which is the origin and (at the same time) the destination, is passed twice. § A graph that contains Hamilton path is also called semi. Hamiltonian graph. § A graph that contains Hamilton circuit is also called Hamiltonian graph. Erwin Sitompul Discrete Mathematics 10/22

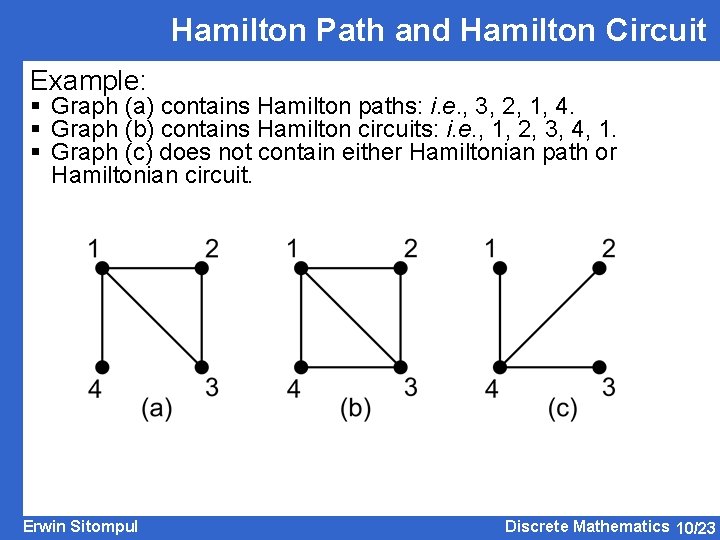
Hamilton Path and Hamilton Circuit Example: § Graph (a) contains Hamilton paths: i. e. , 3, 2, 1, 4. § Graph (b) contains Hamilton circuits: i. e. , 1, 2, 3, 4, 1. § Graph (c) does not contain either Hamiltonian path or Hamiltonian circuit. Erwin Sitompul Discrete Mathematics 10/23

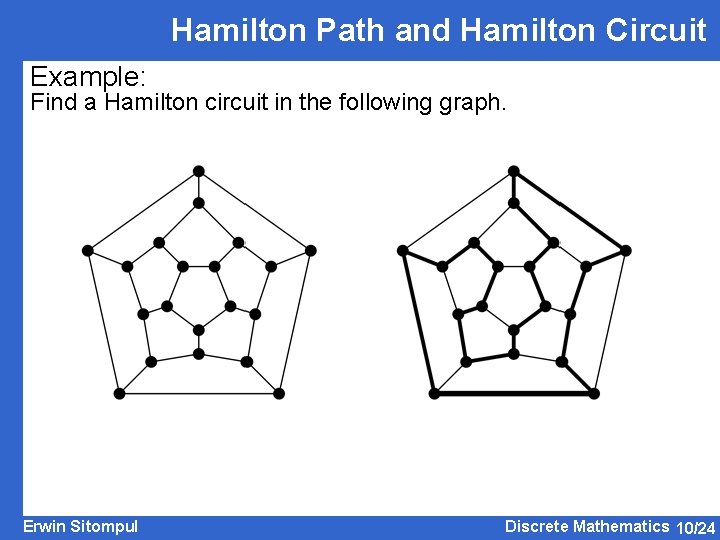
Hamilton Path and Hamilton Circuit Example: Find a Hamilton circuit in the following graph. Erwin Sitompul Discrete Mathematics 10/24

Hamilton Path and Hamilton Circuit Theorem: A sufficient condition for a graph G with the number of vertices n 3 to be a Hamiltonian graph is that the degree of each vertex v in G to be at least n/2, or d(v) n/2. Erwin Sitompul Discrete Mathematics 10/25

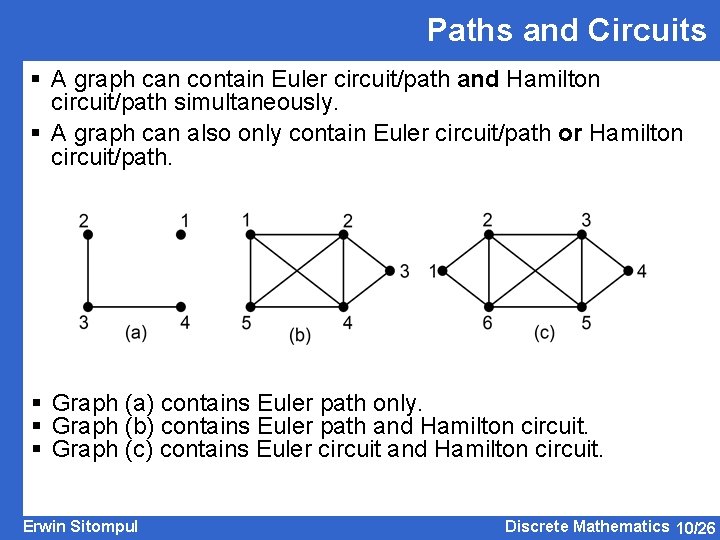
Paths and Circuits § A graph can contain Euler circuit/path and Hamilton circuit/path simultaneously. § A graph can also only contain Euler circuit/path or Hamilton circuit/path. § Graph (a) contains Euler path only. § Graph (b) contains Euler path and Hamilton circuit. § Graph (c) contains Euler circuit and Hamilton circuit. Erwin Sitompul Discrete Mathematics 10/26

Applications of Graphs § Travelling salesman problem. § Chinese postman problem. § Graph coloring. Erwin Sitompul Discrete Mathematics 10/27

Travelling Salesman Problem (TSP) § For this problem, a number of cities and the distances between them are given. § Determine the shortest circuit that must be traveled by a salesman if he departs from a city of origin and stop by in each city exactly once and goes back to the city of origin. § This is a problem of how to find a Hamilton circuit with the minimum weight (distance). Erwin Sitompul Discrete Mathematics 10/28

Applications of TSP § Mr. Postman collects the letters for mailboxes which are distributed in n locations in a certain town. § The robot arm fastens n bolts of a car in an assembly line. § Production process of n different products in one cycle. Erwin Sitompul Discrete Mathematics 10/29

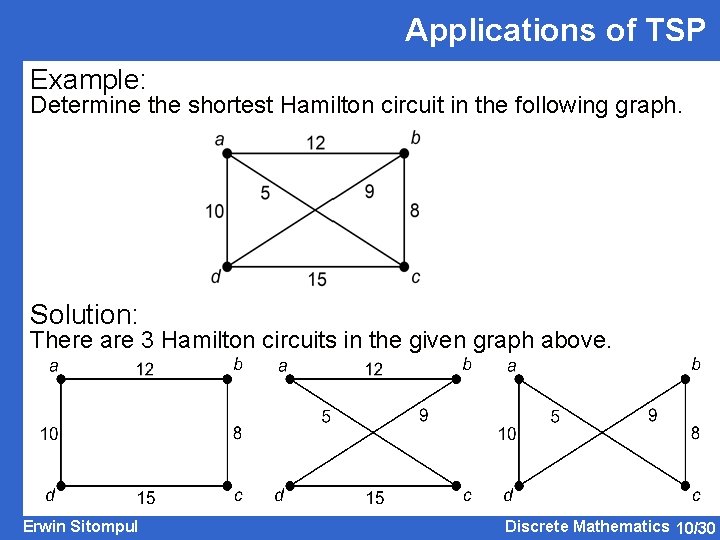
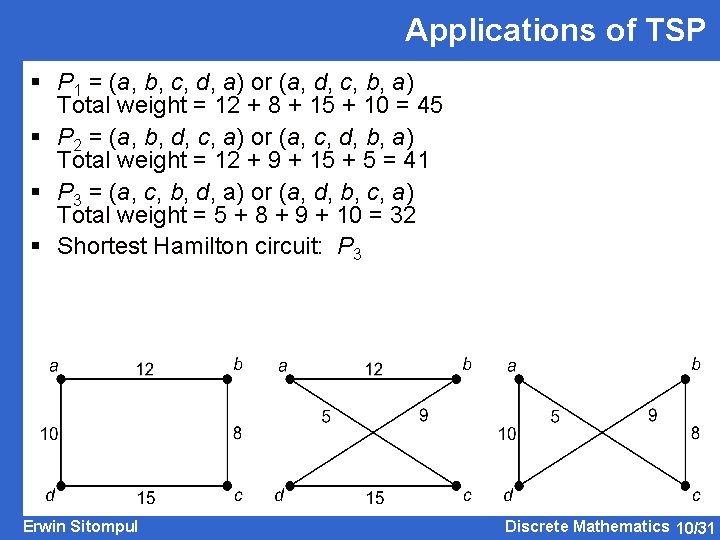
Applications of TSP Example: Determine the shortest Hamilton circuit in the following graph. Solution: There are 3 Hamilton circuits in the given graph above. Erwin Sitompul Discrete Mathematics 10/30

Applications of TSP § P 1 = (a, b, c, d, a) or (a, d, c, b, a) Total weight = 12 + 8 + 15 + 10 = 45 § P 2 = (a, b, d, c, a) or (a, c, d, b, a) Total weight = 12 + 9 + 15 + 5 = 41 § P 3 = (a, c, b, d, a) or (a, d, b, c, a) Total weight = 5 + 8 + 9 + 10 = 32 § Shortest Hamilton circuit: P 3 Erwin Sitompul Discrete Mathematics 10/31

Chinese Postman Problem § The problem was first discussed by Mei Gan in 1962. § Problem: A postman will deliver the letters to the addresses in a part of a city. How should he plan the route of his journey so that he can pass each street exactly once and go back to the place where he starts his journey? § This is a problem of how to find an Euler circuit in a graph. Erwin Sitompul Discrete Mathematics 10/32

Chinese Postman Problem § If the graph of the problem is an Eulerian graph, then the Euler circuit can easily be found. § If the graph of the problem is not an Eulerian graph, then some edges in the graph must be passed more than once. § So, the postman must find a circuit that passes every street at least once with the shortest distance possible. § Chinese Postman Problem becomes: A postman will deliver the letters to the addresses in a part of a city. How should he plan his route so that: § The route has the shortest distance. § The postman passes every street at least once. § The postman goes back to his original position. Erwin Sitompul Discrete Mathematics 10/33

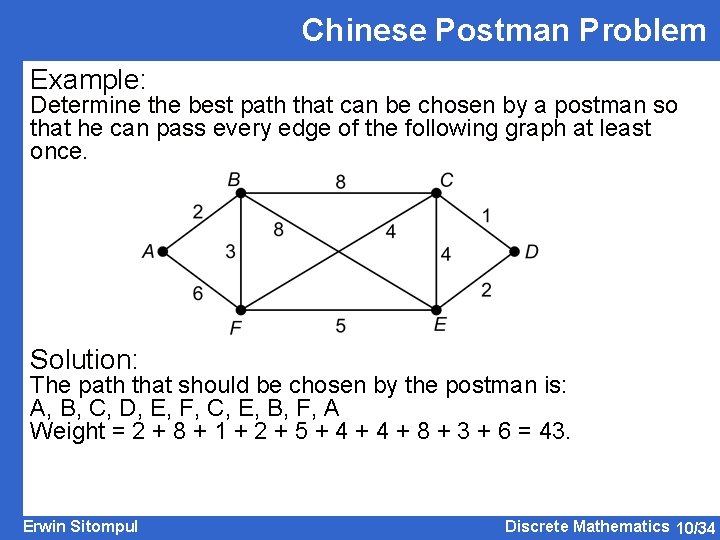
Chinese Postman Problem Example: Determine the best path that can be chosen by a postman so that he can pass every edge of the following graph at least once. Solution: The path that should be chosen by the postman is: A, B, C, D, E, F, C, E, B, F, A Weight = 2 + 8 + 1 + 2 + 5 + 4 + 8 + 3 + 6 = 43. Erwin Sitompul Discrete Mathematics 10/34

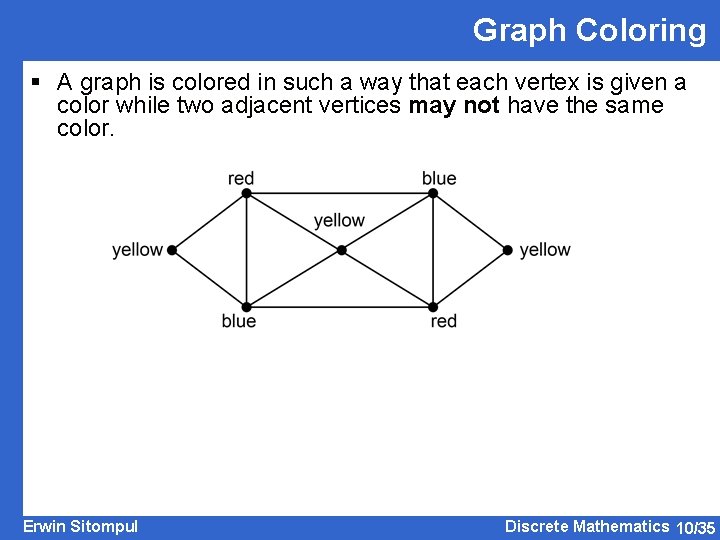
Graph Coloring § A graph is colored in such a way that each vertex is given a color while two adjacent vertices may not have the same color. Erwin Sitompul Discrete Mathematics 10/35

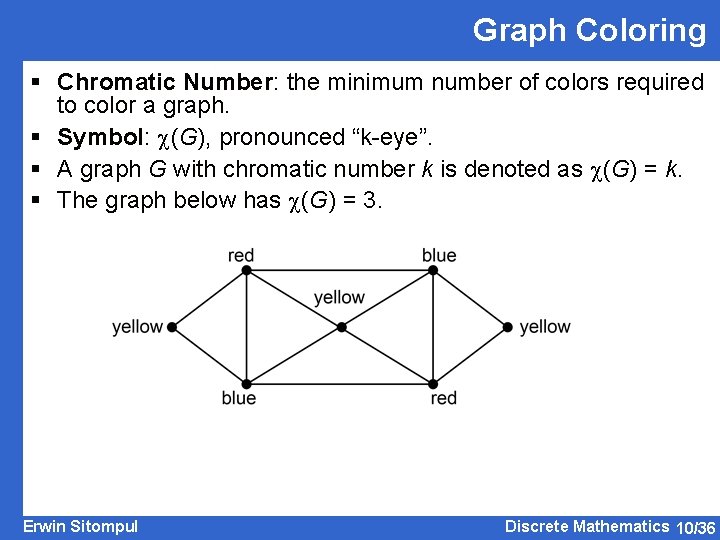
Graph Coloring § Chromatic Number: the minimum number of colors required to color a graph. § Symbol: (G), pronounced “k-eye”. § A graph G with chromatic number k is denoted as (G) = k. § The graph below has (G) = 3. Erwin Sitompul Discrete Mathematics 10/36

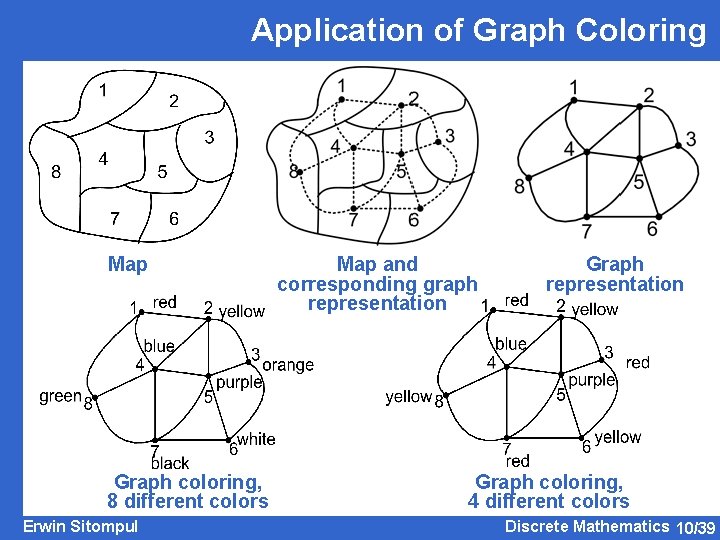
Application of Graph Coloring § Map Coloring § A map consists of a number of regions. § A map should be colored in such a way that two neighboring regions must have different colors. Erwin Sitompul Discrete Mathematics 10/37

Application of Graph Coloring § The regions are represented by the vertices, and the border between two neighboring regions is represented by an edge. § Coloring a region in a map means coloring the vertex in the corresponding graph. § Neighboring regions must have different colors The color of every incident vertices must be different. Erwin Sitompul Discrete Mathematics 10/38

Application of Graph Coloring Map Graph coloring, 8 different colors Erwin Sitompul Map and corresponding graph representation Graph coloring, 4 different colors Discrete Mathematics 10/39

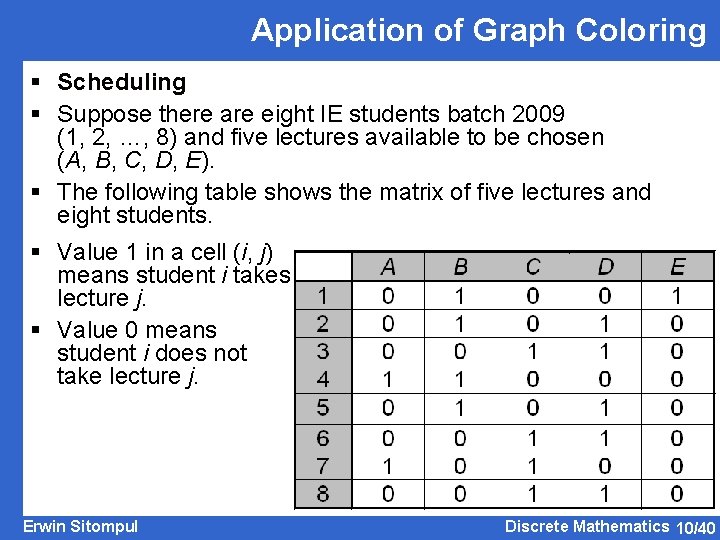
Application of Graph Coloring § Scheduling § Suppose there are eight IE students batch 2009 (1, 2, …, 8) and five lectures available to be chosen (A, B, C, D, E). § The following table shows the matrix of five lectures and eight students. § Value 1 in a cell (i, j) means student i takes lecture j. § Value 0 means student i does not take lecture j. Erwin Sitompul Discrete Mathematics 10/40

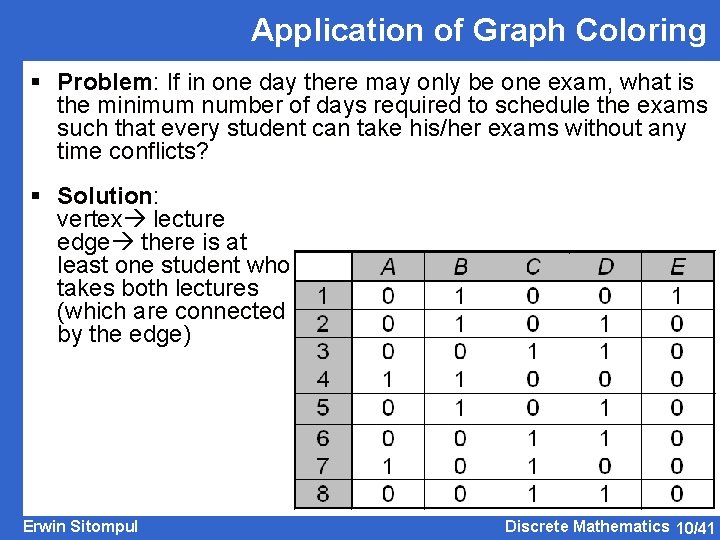
Application of Graph Coloring § Problem: If in one day there may only be one exam, what is the minimum number of days required to schedule the exams such that every student can take his/her exams without any time conflicts? § Solution: vertex lecture edge there is at least one student who takes both lectures (which are connected by the edge) Erwin Sitompul Discrete Mathematics 10/41

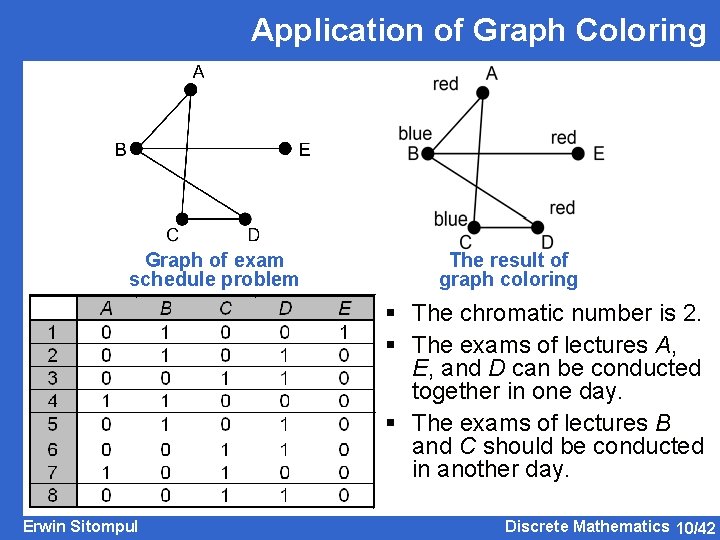
Application of Graph Coloring Graph of exam schedule problem The result of graph coloring § The chromatic number is 2. § The exams of lectures A, E, and D can be conducted together in one day. § The exams of lectures B and C should be conducted in another day. Erwin Sitompul Discrete Mathematics 10/42

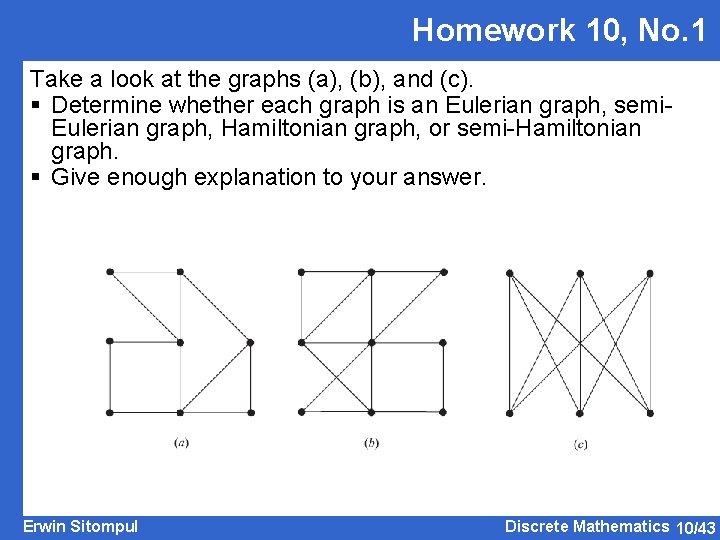
Homework 10, No. 1 Take a look at the graphs (a), (b), and (c). § Determine whether each graph is an Eulerian graph, semi. Eulerian graph, Hamiltonian graph, or semi-Hamiltonian graph. § Give enough explanation to your answer. Erwin Sitompul Discrete Mathematics 10/43

Homework 10, No. 2 A department has six task forces. Every task force conducts a routine monthly meeting. The member of the six task forces are: TF 1 = {Amir, Budi, Yanti} TF 2 = {Budi, Hasan, Tommy} TF 3 = {Amir, Tommy, Yanti} TF 4 = {Hasan, Tommy, Yanti} TF 5 = {Amir, Budi} TF 6 = {Budi, Tommy, Yanti} (a) What is the minimum number of time slots that must be allocated so that everyone that belong to more than one task force can attend the meetings that he/she must join without any time conflict? (b) Draw the graph that represents this problem and explain what do a vertex and an edge represent. Erwin Sitompul Discrete Mathematics 10/44