Its Easier to Approximate David Tse Wireless Foundations

It’s Easier to Approximate David Tse Wireless Foundations U. C. Berkeley ISIT 2009 Seoul, South Korea

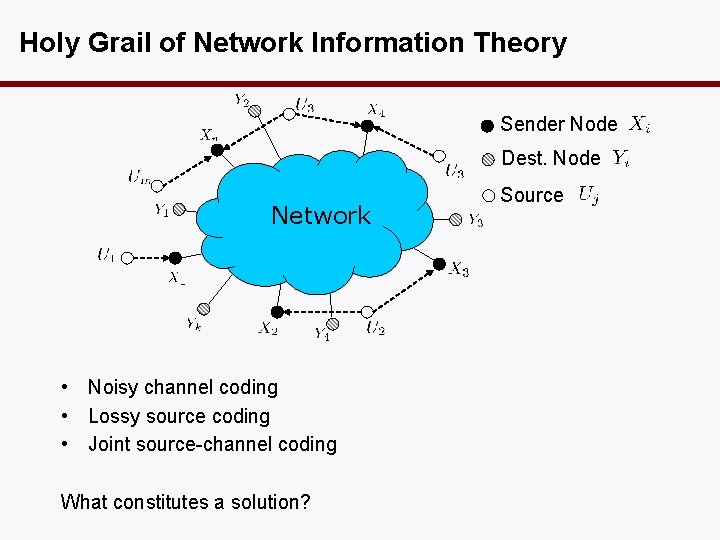
Holy Grail of Network Information Theory Sender Node Dest. Node Network • Noisy channel coding • Lossy source coding • Joint source-channel coding What constitutes a solution? Source

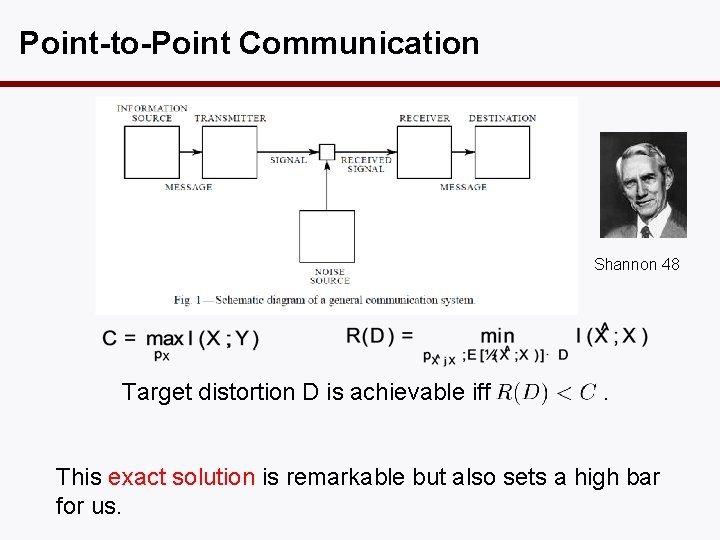
Point-to-Point Communication Shannon 48 Target distortion D is achievable iff . This exact solution is remarkable but also sets a high bar for us.

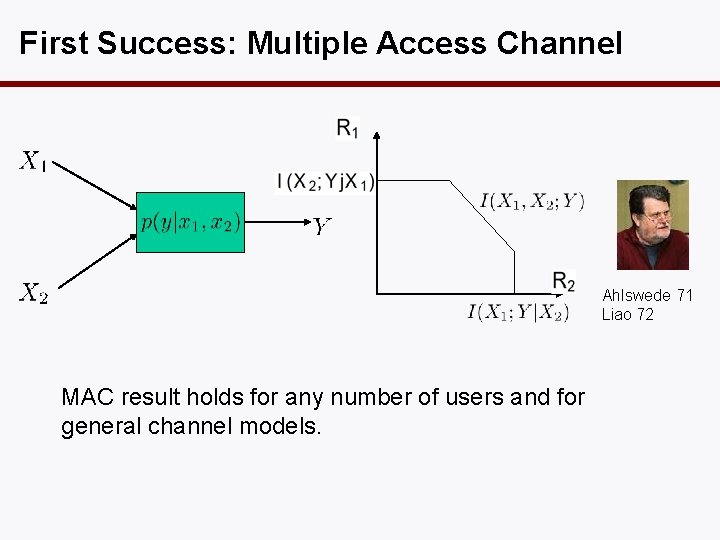
First Success: Multiple Access Channel Ahlswede 71 Liao 72 MAC result holds for any number of users and for general channel models.

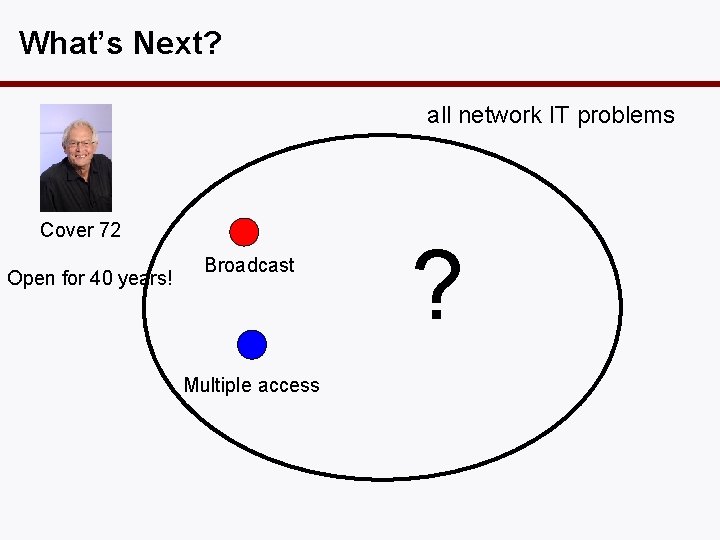
What’s Next? all network IT problems Cover 72 Open for 40 years! Broadcast Multiple access ?

Gaussian Problems • practically relevant • physically meaningful • provide worst-case bounds Are they easier?

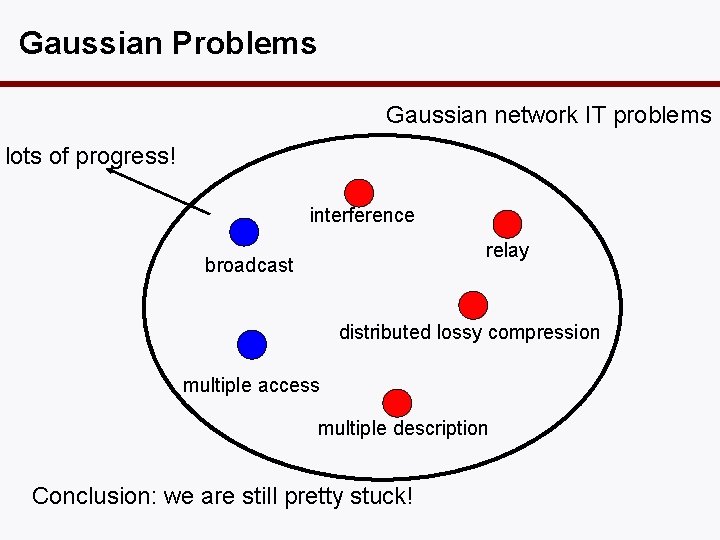
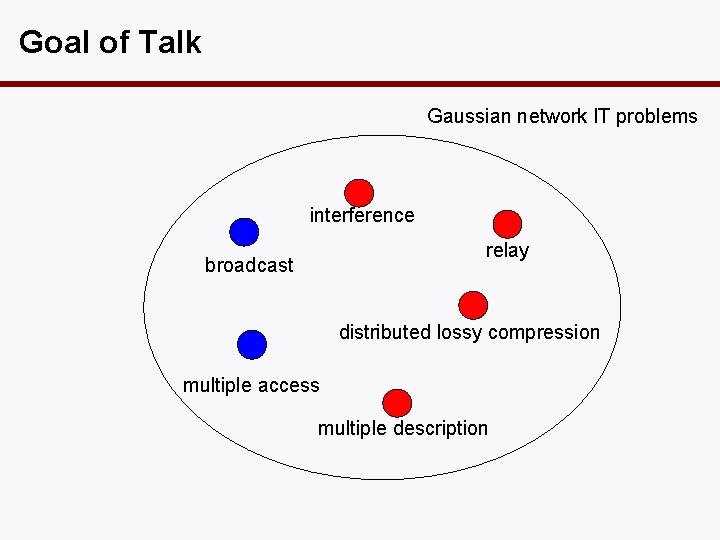
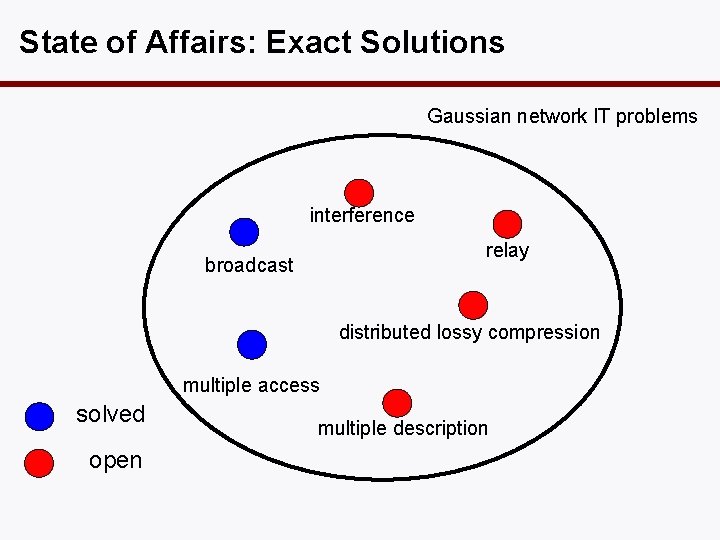
Gaussian Problems Gaussian network IT problems lots of progress! interference relay broadcast distributed lossy compression multiple access multiple description Conclusion: we are still pretty stuck!

New Strategy: Approximate! • Look for approximate solutions with guarantee on gap to optimality. • Approximation results are not new. • We advocate a systematic approach to apply to many problems.

Approximation Approach 1) Simplify: – Channel coding: noisy to noiseless – Source coding: lossy to lossless 2) Analyze simplified problem. 3) Use insight to find new schemes and outer bounds for Gaussian problem. 4) Derive worst-case gap.

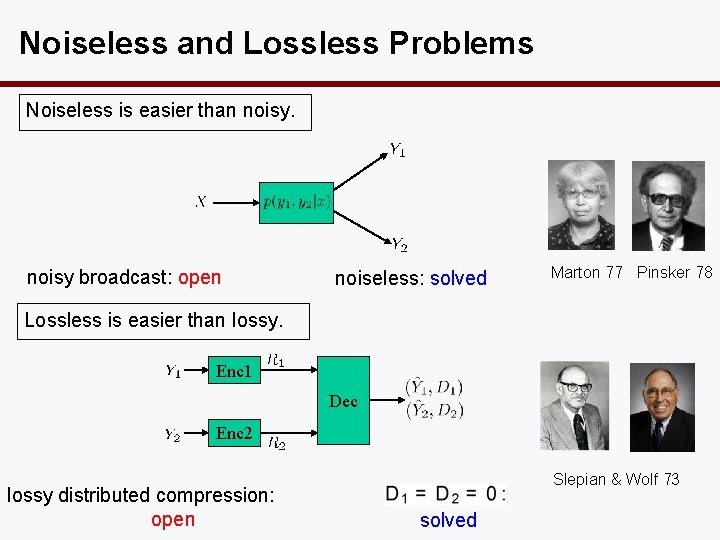
Noiseless and Lossless Problems Noiseless is easier than noisy broadcast: open noiseless: solved Marton 77 Pinsker 78 Lossless is easier than lossy. Enc 1 Dec Enc 2 lossy distributed compression: open Slepian & Wolf 73 solved

Goal of Talk Gaussian network IT problems interference relay broadcast distributed lossy compression multiple access multiple description

1. Interference

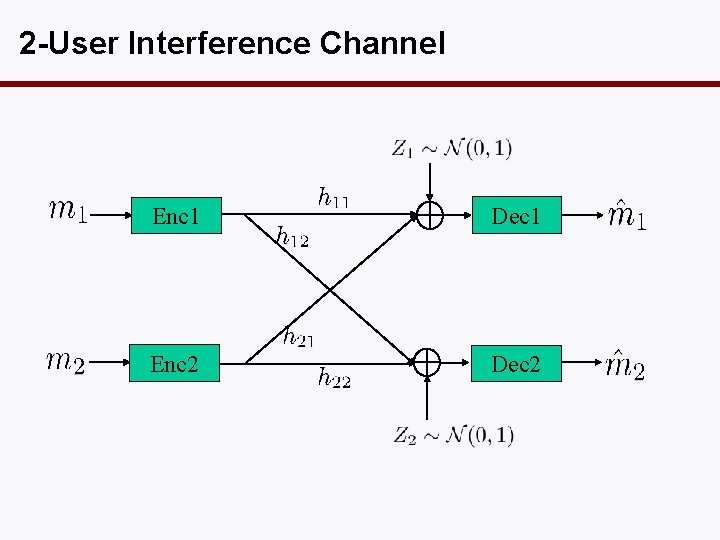
2 -User Interference Channel Enc 1 Dec 1 Enc 2 Dec 2

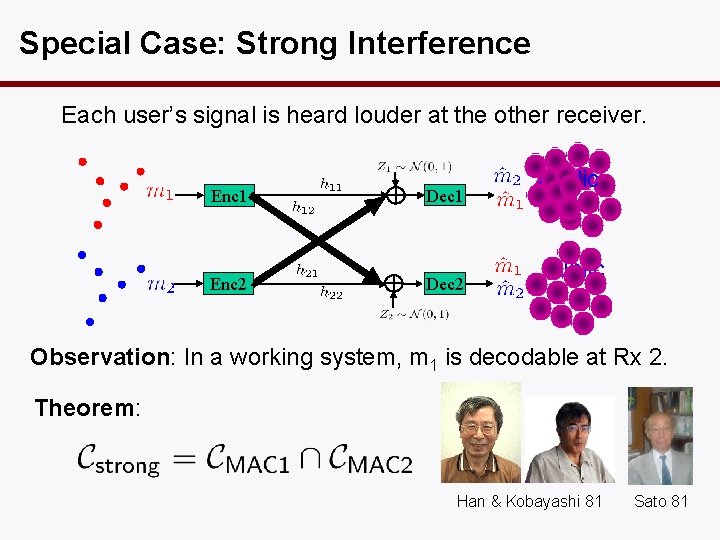
Special Case: Strong Interference Each user’s signal is heard louder at the other receiver. Enc 1 Dec 1 Enc 2 Dec 2 public Observation: In a working system, m 1 is decodable at Rx 2. Theorem: Han & Kobayashi 81 Sato 81

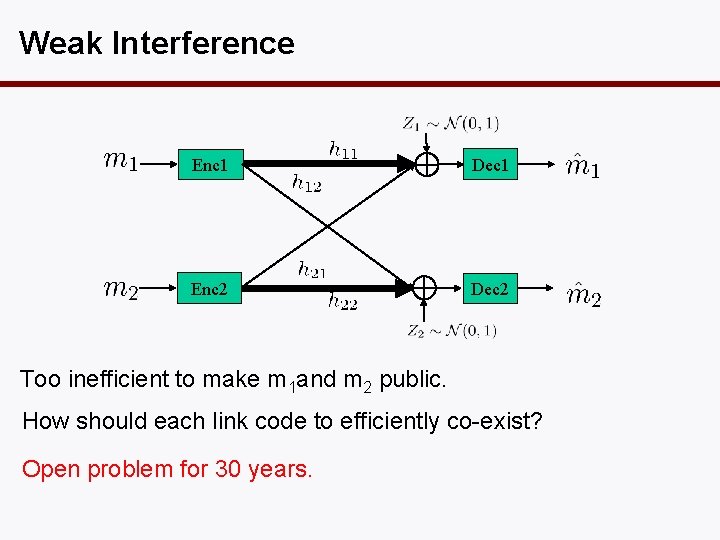
Weak Interference Enc 1 Dec 1 Enc 2 Dec 2 Too inefficient to make m 1 and m 2 public. How should each link code to efficiently co-exist? Open problem for 30 years.

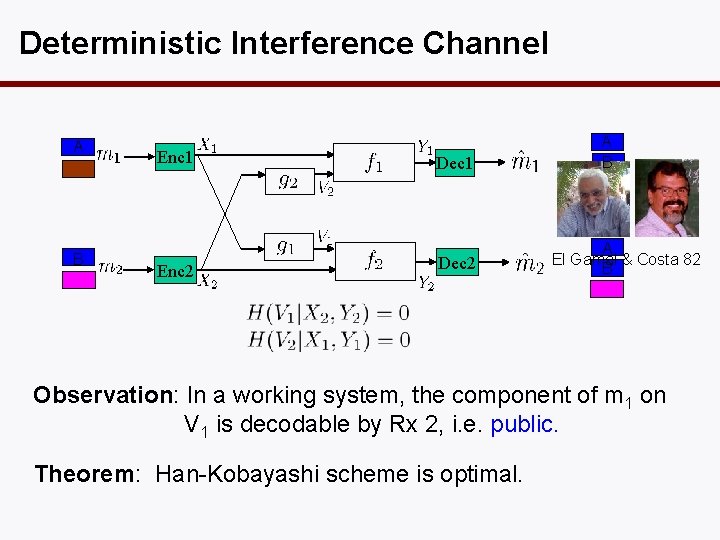
Deterministic Interference Channel A B Enc 1 Enc 2 Dec 1 Dec 2 A B A El Gamal & Costa 82 B Observation: In a working system, the component of m 1 on V 1 is decodable by Rx 2, i. e. public. Theorem: Han-Kobayashi scheme is optimal.

Connection to Gaussian Problem public private V 1 Is there a natural V 1?

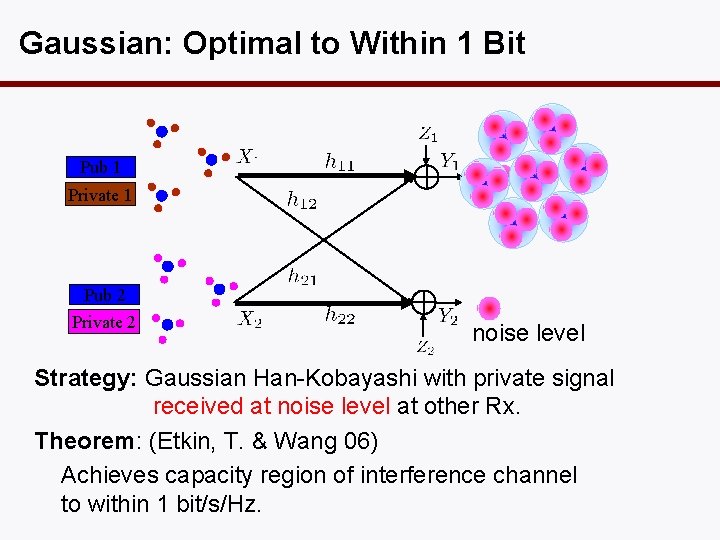
Gaussian: Optimal to Within 1 Bit Pub 1 Private 1 Pub 2 Private 2 noise level Strategy: Gaussian Han-Kobayashi with private signal received at noise level at other Rx. Theorem: (Etkin, T. & Wang 06) Achieves capacity region of interference channel to within 1 bit/s/Hz.

New Strategies? • Gaussian Han-Kobayashi turns out to be quite good for the 2 user interference channel. • How about for more users?

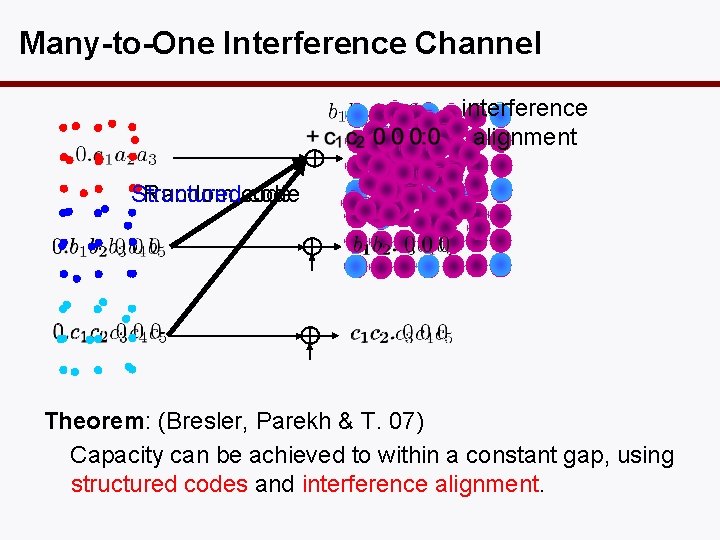
Many-to-One Interference Channel interference alignment Random code Structured code Theorem: (Bresler, Parekh & T. 07) Capacity can be achieved to within a constant gap, using structured codes and interference alignment.

Open Question Find a constant gap approximation to the general Kuser interference channel,

2. Relay

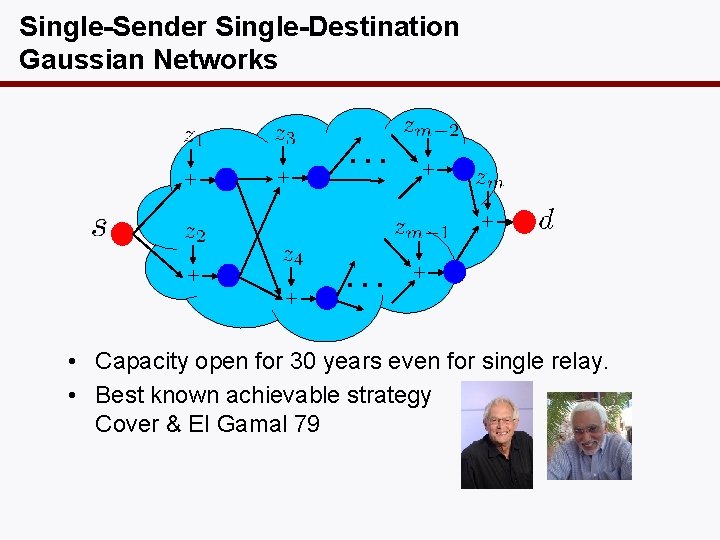
Single-Sender Single-Destination Gaussian Networks … … • Capacity open for 30 years even for single relay. • Best known achievable strategy Cover & El Gamal 79

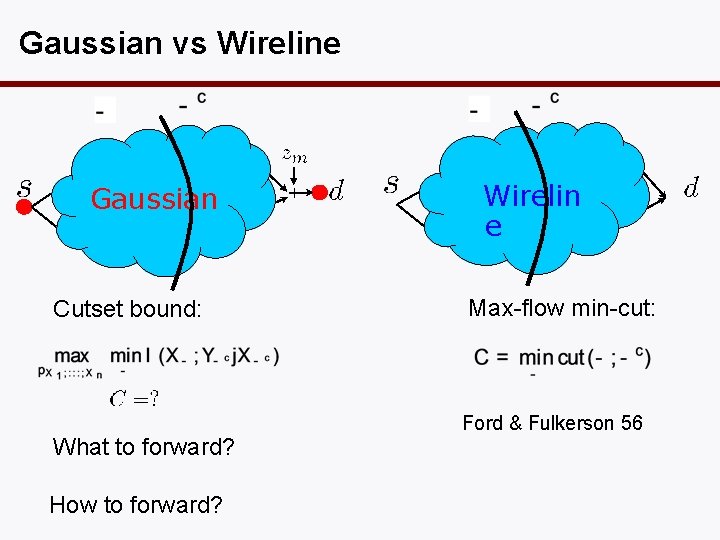
Gaussian vs Wireline Gaussian Cutset bound: What to forward? How to forward? Wirelin e Max-flow min-cut: Ford & Fulkerson 56

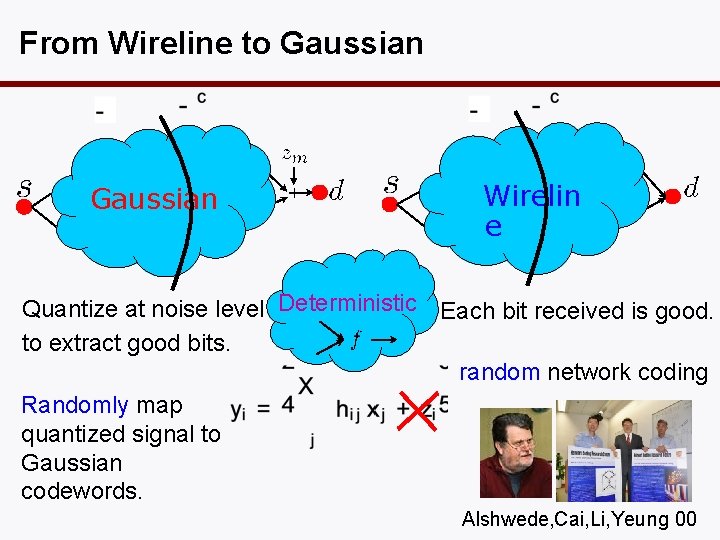
From Wireline to Gaussian Wirelin e Quantize at noise level Deterministic Each bit received is good. to extract good bits. random network coding Randomly map quantized signal to Gaussian codewords. Alshwede, Cai, Li, Yeung 00

Approximate Max-Flow Min-Cut Theorem: (Avestimehr, Diggavi & T. 08) Quantize-and-random-map strategy achieves where the gap does not depend on the channel gains. Not true for classic schemes: – Decode-and-forward – amplify-and-forward, – Gaussian compress-and-forward

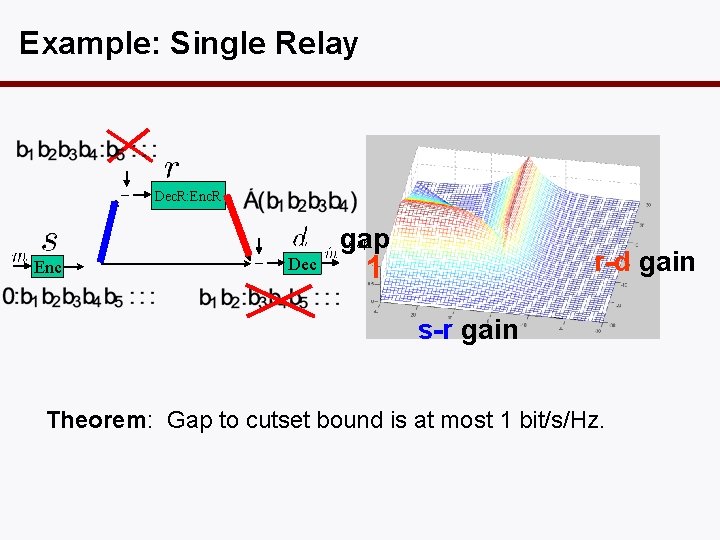
Example: Single Relay Dec. R: Enc. R Enc Dec gap r-d gain 1 s-r gain Theorem: Gap to cutset bound is at most 1 bit/s/Hz.

Scaling with Network Size Bit of a bad news: gap increases with # of nodes Open question: Is the gap of the capacity to the cutset bound universal of # of nodes also?

Lossy Source Coding

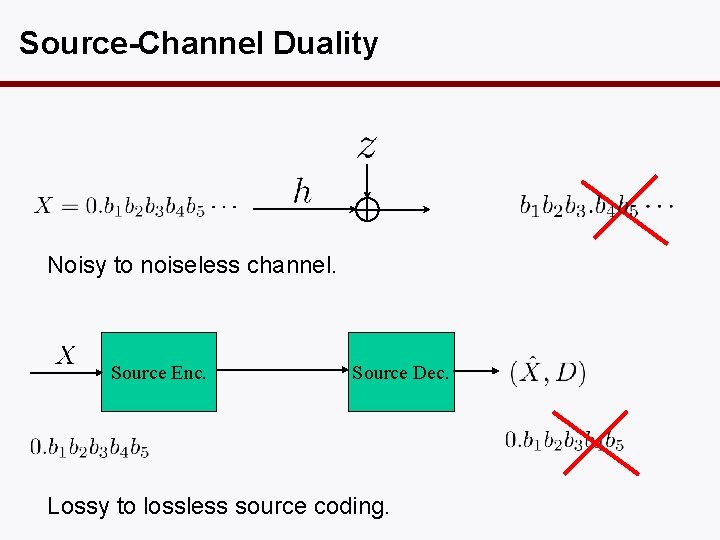
Source-Channel Duality Noisy to noiseless channel. Source Enc. Source Dec. Lossy to lossless source coding.

3. Multiple Description

Gaussian Multiple Description Gaussian Enc 1 Dec 1 A Dec 2 Enc 2 Dec 1 B • Rate region solved for K=2 descriptions (Ozarow 80) • What about for K>2 descriptions? • Symmetric case: want same distortion Dm for any subset of m descriptions.

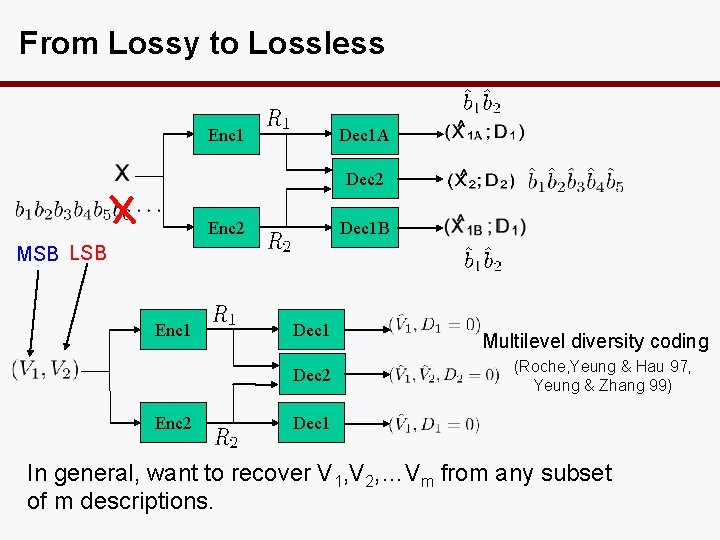
From Lossy to Lossless Enc 1 Dec 1 A Dec 2 Enc 2 Dec 1 B MSB LSB Enc 1 Dec 2 Enc 2 Multilevel diversity coding (Roche, Yeung & Hau 97, Yeung & Zhang 99) Dec 1 In general, want to recover V 1, V 2, …Vm from any subset of m descriptions.

Symmetric Multilevel Diversity Coding LSB (3, 3) no coding (3, 2) MDS code MSB (3, 1) repetition code Description 1 Description 2 Description 3

Back to Gaussian Lossy Problem Gaussian Successive Refinement Code Multilevel Diversity Coding Theorem: (Tian, Mohajer & Diggavi 08) This scheme can achieve within 1. 48 bits/sample of the symmetric rate point for any # of descriptions. A more sophisticated scheme (Puri, Pradhan, Ramchandran 05) has a gap of 0. 92 bits.

4. Distributed Lossy Compression

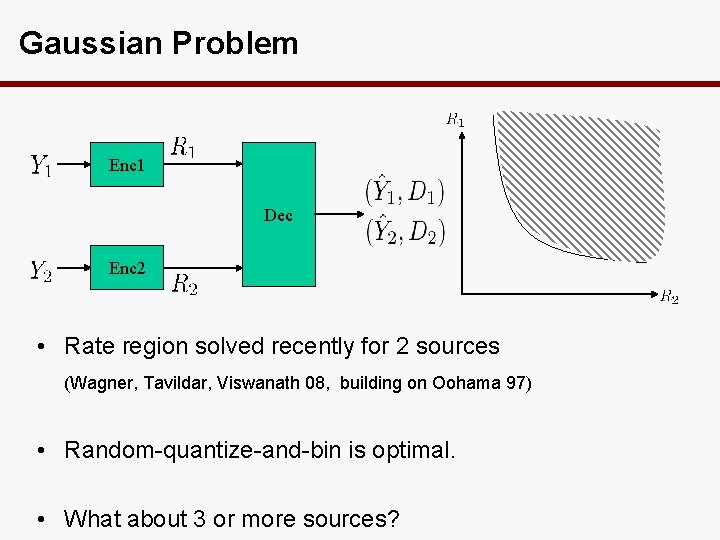
Gaussian Problem Enc 1 Dec Enc 2 • Rate region solved recently for 2 sources (Wagner, Tavildar, Viswanath 08, building on Oohama 97) • Random-quantize-and-bin is optimal. • What about 3 or more sources?

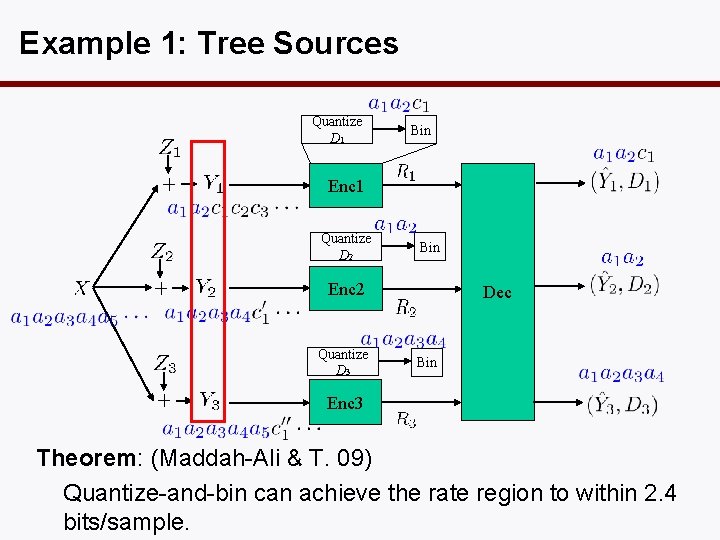
Example 1: Tree Sources Quantize D 1 Bin Enc 1 Quantize D 2 Bin Enc 2 Quantize D 3 Dec Bin Enc 3 Theorem: (Maddah-Ali & T. 09) Quantize-and-bin can achieve the rate region to within 2. 4 bits/sample.

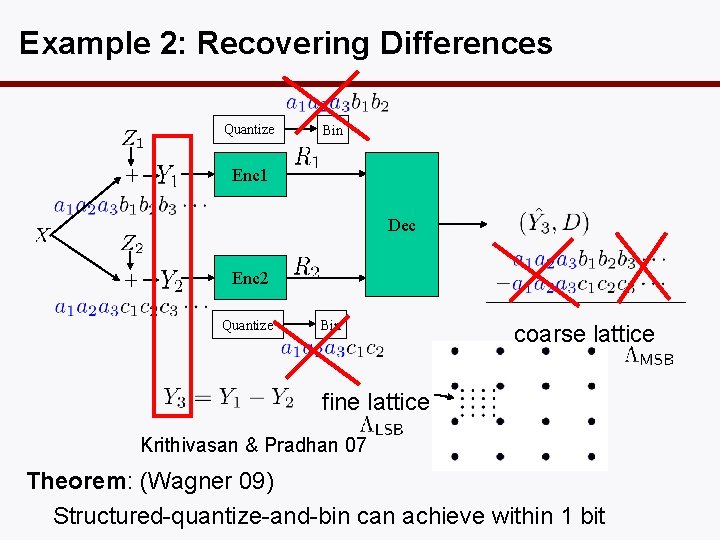
Example 2: Recovering Differences Quantize Bin Enc 1 Dec Enc 2 Quantize Bin coarse lattice fine lattice Krithivasan & Pradhan 07 Theorem: (Wagner 09) Structured-quantize-and-bin can achieve within 1 bit

State of Affairs

State of Affairs: Exact Solutions Gaussian network IT problems interference relay broadcast distributed lossy compression multiple access solved open multiple description

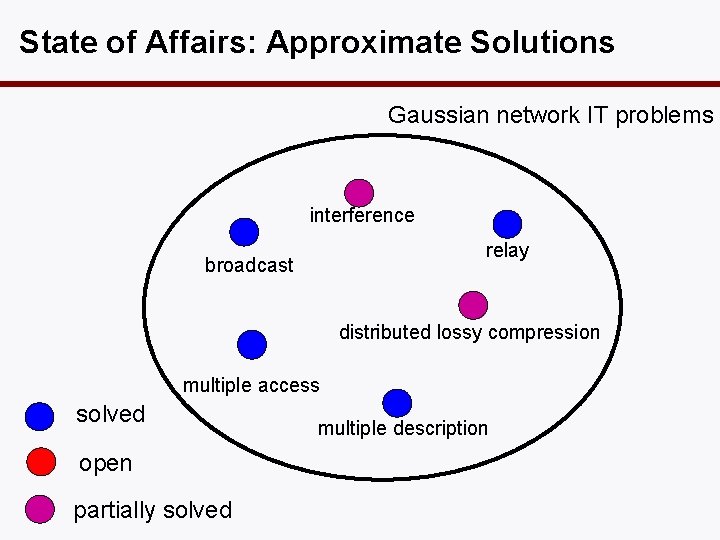
State of Affairs: Approximate Solutions Gaussian network IT problems interference relay broadcast distributed lossy compression multiple access solved open partially solved multiple description

Collaborators Raul Etkin Abhay Parekh Hua Wang Salman Avestimehr Randy Berry Mohammad Maddah-Ali Changho Suh Guy Bresler Suhas Diggavi Roy Yates Emre Telatar Vinod Prabhakaran