Wireless Communications Wireless Communications Wireless is more and

Wireless Communications

Wireless Communications • Wireless is more and more widely deployed – cellphone, wireless LAN, … • The fundamental fact is that if the sender sends a sine wave, the receiver will receive a sine wave at the same frequency. But with – A different phase – A new amplitude • How do you design communication schemes based on that?

Wireless Communications • AM – stronger signal when `1’, weaker signal when `0’. • FM – faster waveform when `1’, slower signal when `0’. • BPSK – 0 degree when `0’, 180 degree when `1’.

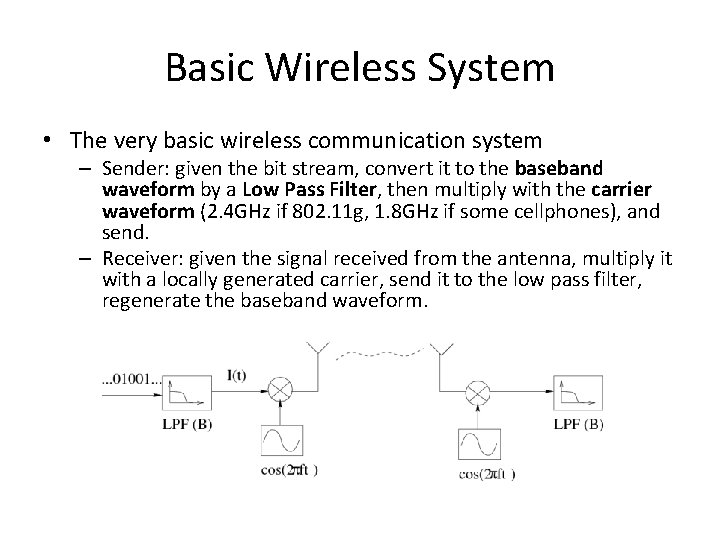
Basic Wireless System • The very basic wireless communication system – Sender: given the bit stream, convert it to the baseband waveform by a Low Pass Filter, then multiply with the carrier waveform (2. 4 GHz if 802. 11 g, 1. 8 GHz if some cellphones), and send. – Receiver: given the signal received from the antenna, multiply it with a locally generated carrier, send it to the low pass filter, regenerate the baseband waveform.

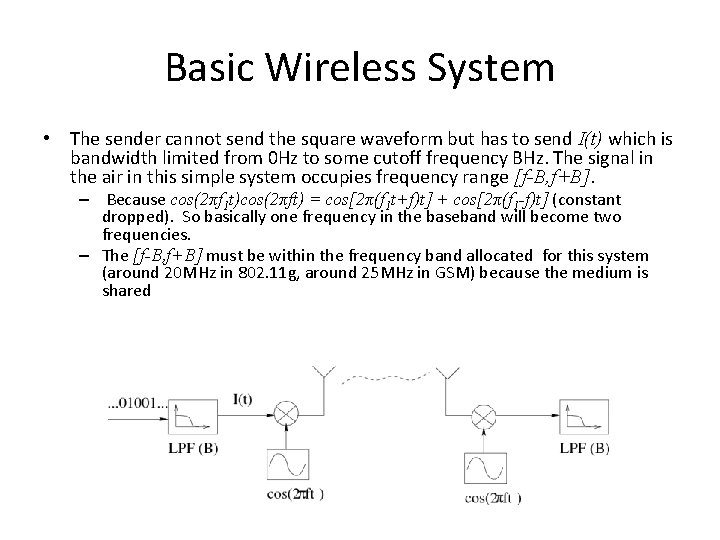
Basic Wireless System • The sender cannot send the square waveform but has to send I(t) which is bandwidth limited from 0 Hz to some cutoff frequency BHz. The signal in the air in this simple system occupies frequency range [f-B, f+B]. – Because cos(2πf 1 t)cos(2πft) = cos[2π(f 1 t+f)t] + cos[2π(f 1 -f)t] (constant dropped). So basically one frequency in the baseband will become two frequencies. – The [f-B, f+B] must be within the frequency band allocated for this system (around 20 MHz in 802. 11 g, around 25 MHz in GSM) because the medium is shared

Basic Wireless System • How can the receiver regenerate the baseband waveform? A simplified explanation: – The sender sends I(t)cos(2πft). – Assume there is no phase difference, the receiver multiplies I(t)cos(2πft) with cos(2πft), and gets I(t)cos 2(2πft) = I(t)[1/2 + 1/2 cos(4πft)]. – Then, after the low pass filter, what is left is the low frequency component I(t). – http: //math 2. org/math/trig/identities. htm

Two Orthogonal Channels • The sender sends I(t)cos(2πft) + Q(t)sin(2πft). • The receiver multiplies the received signal with cos(2πft) , and will get [I(t)cos(2πft) + Q(t)sin(2πft)] cos(2πft) = I(t)[1+cos(4πft)] + Q(t) sin(4πft) (constant dropped), and after the LPF, will have I(t). • At the same time, the receiver also multiplies the received signal with sin(2πft) , and will get [I(t)cos(2πft) + Q(t)sin(2πft)] sin(2πft) = I(t) sin(4πft) + Q(t) [1 -cos(4πft)] (constant dropped), and after the LPF, will have Q(t). • So, the sender can send TWO baseband waveforms at the same time. Each baseband waveform can carry one voltage value, so a symbol is a point on the two-dimensional plane. We often use a complex number to represent the symbol, where the value in I(t) is the real part and the value in Q(t) is the imaginary part.

BPSK, QAM • BPSK is using only one channel. And in this channel, only two possible voltages. • Quadrature phase-shift keying (QPSK) is using both channels. In each channel, only two voltages. • Quadrature amplitude modulation (QAM) is using both channels. In each channel, multiple voltages. If 4 levels of voltage, it is 16 QAM. If it 8 levels of voltage, 64 QAM.

After Getting the Baseband Signal • The baseband signal is a continuous waveform. • You have to run an algorithm on that to convert the continuous waveform into bits. • Main constraint of the algorithm: should run very fast, i. e. , capable of making a decision every symbol time, must be implemented in hardware, cost is issue.

Issues • How to offset the phase difference from the sender to the receiver? • How to take samples at the right time? • How to get rid of the residual values from nearby symbols, i. e. , dealing with multipath? – In wireless channels, when the sender sends one waveform, the receiver will receive many copies of it, with different phase offset, because the signal travels multiple paths with reflecting surfaces like the metal door, wall, etc. – When taking a sample, the sample could be the best for the strongest path, but may not be for other paths. So some residual voltage from the previous symbol will show up.

Exercise • Consider an 802. 11 g device A transmitting at channel 1 which is 2. 412 GHz. There is another 802. 11 g device B tuned to channel 6 which is 2. 437 GHz. Assume B is in transmission range of A. Why won’t B respond to A’s transmission? (a). Because B’s antenna cannot respond to waveforms centered at 2. 412 GHz. (b). Because B’s local sine wave is at 2. 437 GHz, and after multiplying it with the received waveform, the result is 0. (c). Because B’s upper layer software will filter out packets from other channels. (d). None of the above.

Exercise • An 802. 11 g channel has bandwidth of 20 MHz. Which of the following statements is true? (a). Due to the bandwidth constraint, the highest data rate of 802. 11 g cannot be more than 20 Mbps. (b). The bandwidth constraint limits the highest achievable speed, but the actual speed also depends on the strength of the channel. (c). An 802. 11 g transmitter transmits at the center of the channel frequency so the bandwidth limit has no effect on the speed. (d). None of the above.

Exercise • Which of the following statements about the baseband signal is true? (a). The baseband signal refers to the signal after the low pass filer. (b). The baseband signal is bandwidth-limited. (c). Both of the above. (d). None of the above.

Exercise • In wireless transmissions, we often use the terms ``sample’’ and ``symbol. ’’ Which of the following statements is true? (a). A symbol is a complex number. A BPSK symbol is either -1 or 1. (b). A sample is a complex number. A BPSK sample is either -1 or 1. (c). Both of the above. (d). None of the above.

Exercise • With GNU Software Defined Radio, the transmitter and the receiver can operate at 500 K symbols per second. Which of the following statement is true? (a). It means that we can send one symbol per 2 microseconds. (b). It means that our data rate is 1 Mbps if we use QPSK. (c). Both of the above. (d). None of the above.

Some Important Concepts • • • Bandwidth – How fast can signals change. Or, the width of the frequency range that can pass the system. Noise – Will be added to the signal. Random, but some statistics can be known with which we make our detection rules. Data rate – How fast can we send bits, can be measured in bps. Upper bounded by the Shannon’s theorem given the bandwidth and noise. Propagation delay – How long does it take for the symbol to reach to the destination. Symbol – A point on the plane to represent one bit or multiple bits. Sample – A reading of the received signal at some time instant. Usually a corrupted version of the symbol. Filter – Some device or software that can remove certain frequency components in the received waveform. Carrier – A sine wave to be multiplied with the baseband waveform. Baseband waveform – The waveform that is a smoothed version of the square waveform after the low pass filter. To be multiplied with the carrier.