Integration Esme n Esme is approaching her last





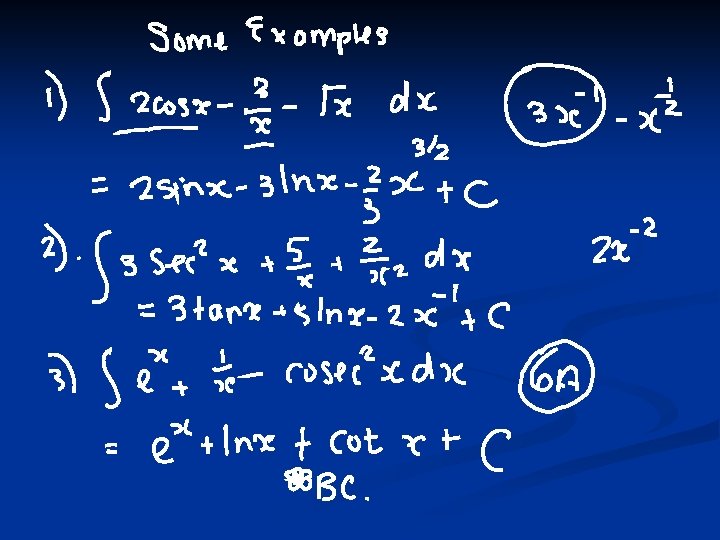

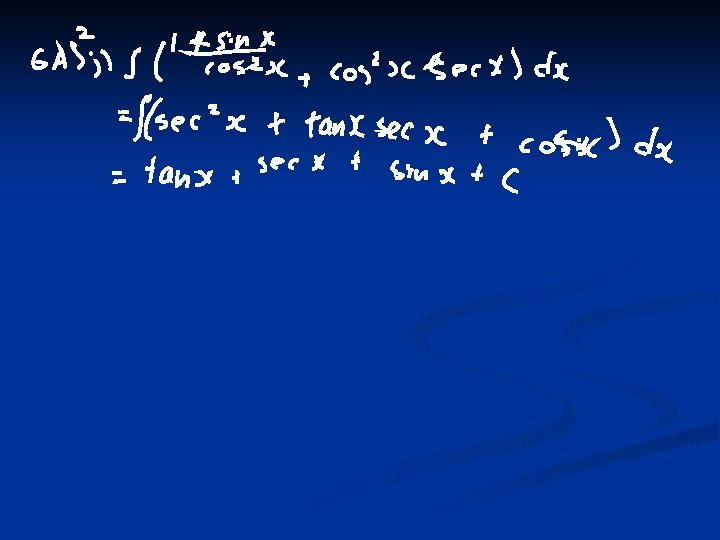














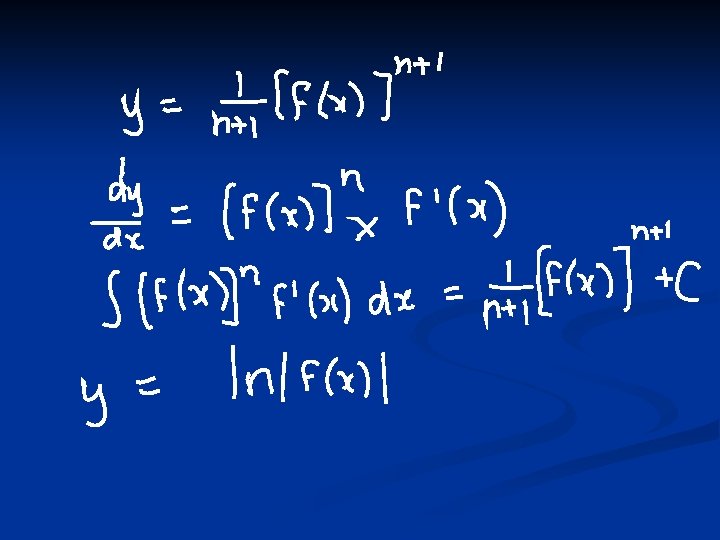























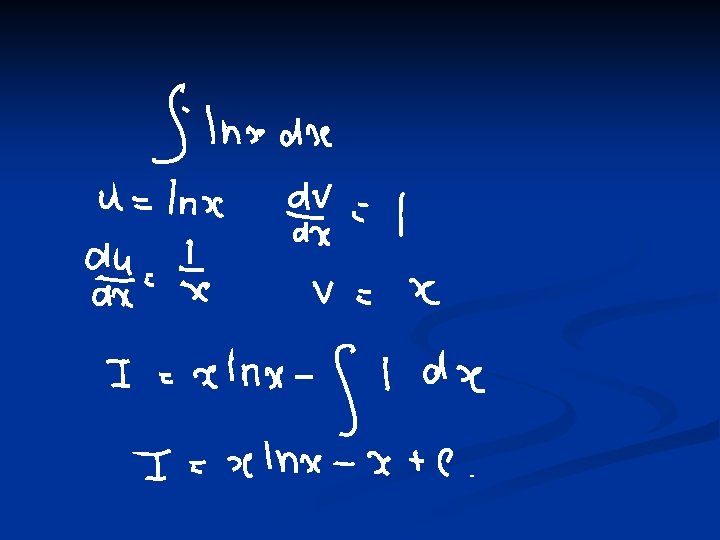





























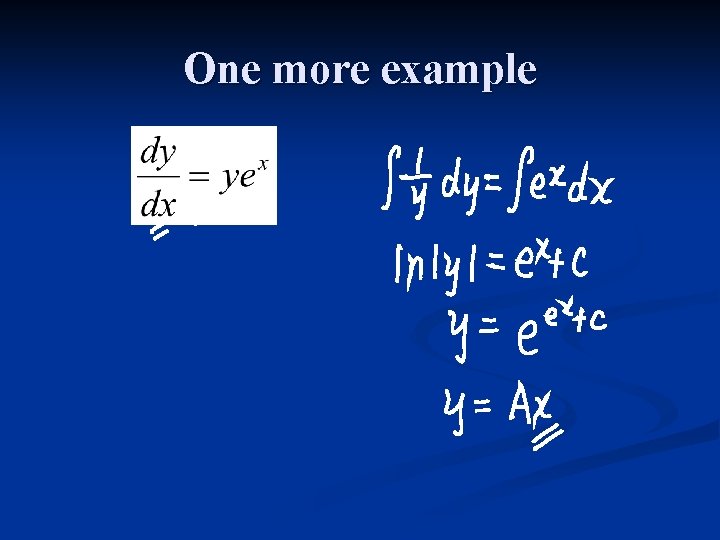



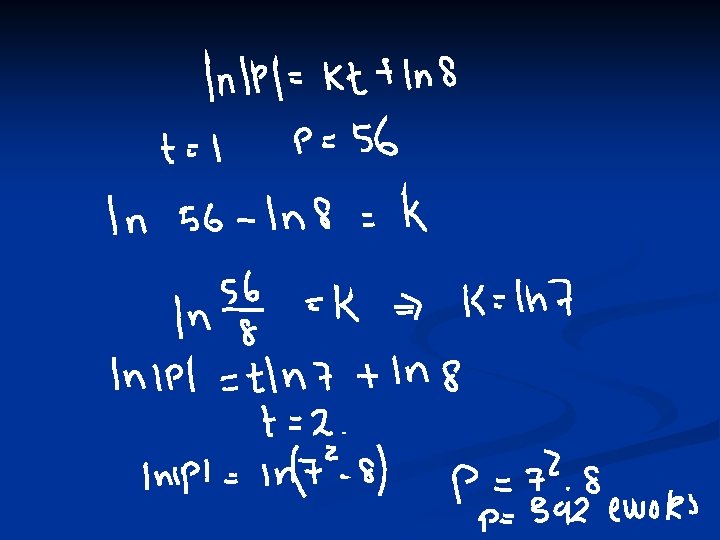

- Slides: 85

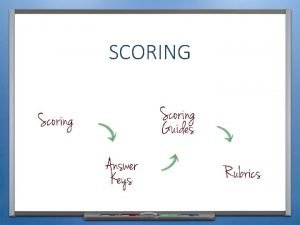
Integration

Esme n Esme is approaching her last topic in her Al level mathematics programme. She goes for a walk through the forest to reflect on her two years of study and for her love of mathematics. Esme stumbles across a very special tree.

The Integration Methods Tree Standard Integrals n Inverse of Chain rule n Using Trig Identities n Partial fractions n Substitution n Integration by Parts n

A little later Integration Applications Finding the area using integration and trapezium rule n Finding the volumes of solids of revolution n

Branch 1 Standard Integrals n Match the integral with the correct answers.

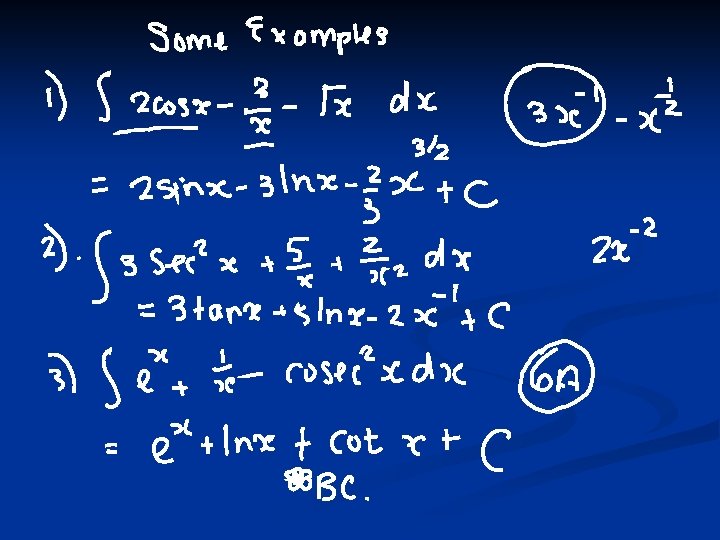

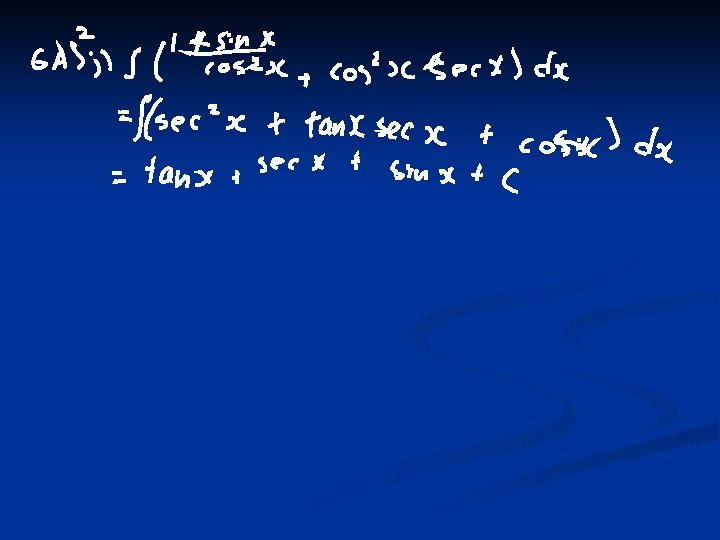

Branch 2 Reverse of the Chain Rule Instead of putting the power in front and dropping the power by one and multiplying by the derivative of the bit in the middle n Y = (2 x+4)6 n Y’ = 6(2 x+4)5 X 2 n We raise the power by one, divide by that power and divide by the derivative of the bit in the middle n

The Magic Phrase We raise the power by one, divide by that power and divide by the derivative of the bit in the middle n

Example

Branch 3 Using trig identities to Integrate Do you remember all our trig identities from C 3? n Write down as many as you can remember n

Example 1

More Examples

Example



Branch 4 Using partial fractions n n We can use partial fractions to integrate expressions that are too long to do other methods with! What are those rules again?


Ex 6 D Question 1 e

Examples

Improper Fraction
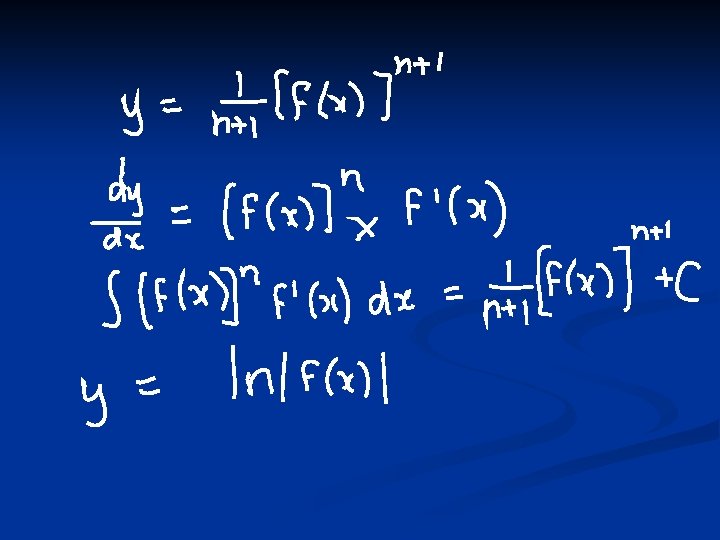

More Standard Integrals Recognizing

Recognizing the Reverse of the Chain Rule

Recognizing Ln and reverse of Chain rule! n Here remember :

Examples

Example

Another example

Your example

Your example

A volunteer

A volunteer

Branch 5 Integration using Substitution n Here is another post it lesson! Sometimes it is much easier to substitute a simpler function that we can easily integrate Integrate the following using the substitution provided

Example 1 Remember to substitute back and c!

Example 3

Example 3

Definite Integrals Here remember to change your boundaries using the substitution you have used n Let’s look at the first example but this time we want to evaluate this integral from x = 1 to x= 3 n

Example 4 Here you can use the new boundaries 7 and 11! No need to add c or substitute back! Why?



Branch 6 Using Integration by Parts n Do you remember the product rule to differentiate the product of two functions? n Or in words v du + u dv We can actually rearrange this to help us to integrate two functions multiplied together! n

Integration by parts Rearranging Integrating

Integration by parts how do I use this?

Example 2

Example 3 with boundaries
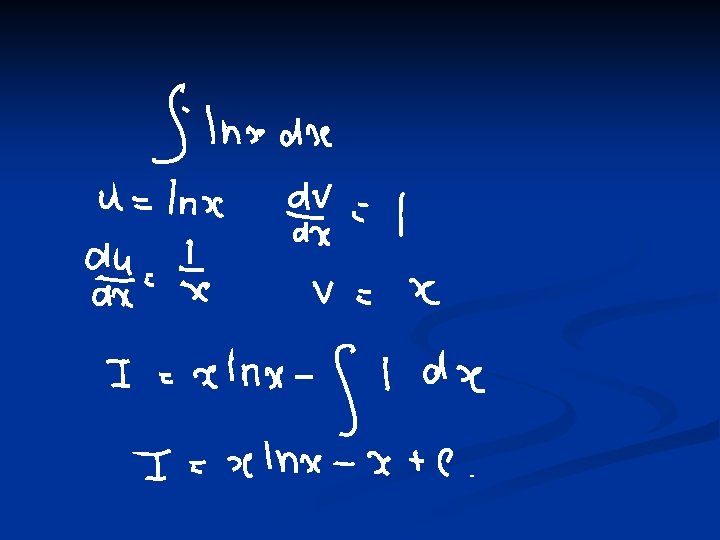

Five review questions

Five review questions

Five review questions

Five review questions

Five review questions

Five review questions

Integrals given in your formulae booklet

Where do they come from?

Trapezium rule revisited n Do you remember this from C 2? Why? n Use a little table as this helps with your working!

Where does this symbol come from? n We know that the integral sign is really the Germanic long "s" as used by Leibniz, and is used to denote the limit of the sum of an increasingly large number of decreasingly sized divisions of an area.

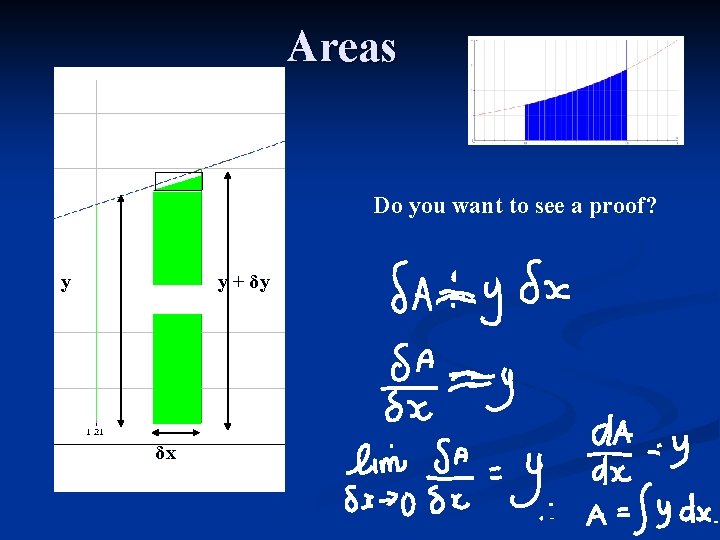
General Areas n So in general the area of a curve y = f(x) which is bound by the lines x = a and x = b and the x axis can be found by

Areas Do you want to see a proof? y δA δx y + δy

Drawing a sketch will help you to determine whether you need to split up your boundary conditions. n Remember any region below the x- axis will give a negative result! n Using you GDC-follow these instructions n

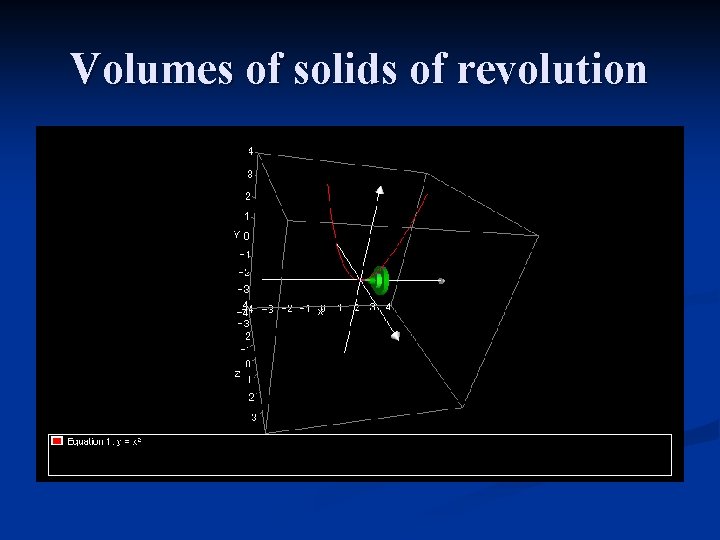
Volumes of solids of revolution n An applet increasing the number of discs

Volumes of solids of revolution

Volumes of solids of Revolution

Example 1 n Find the area and volume of the solid generated by the curve:

Example 1 n Find the area and volume of the solid generated by the curve:

Example 2 n n n The region R is bound by the curve C, the x axis and the lines x=-8 and x=8. The parametric equations for C are x=t 3 and y=t 2. Find the area of R Find the volume of solid of revolution formed when R is rotated about the x axis.


Example 3 volumes n n n The curve has parametric equations x=sin t and y=sin 2 t where 0<t< /2. Find the area bound by the curve Find the volume of solid generated about the x axis.

Example 3 volumes n n n The curve has parametric equations x=sin t and y=sin 2 t where 0<t< /2. Find the area bound by the curve Find the volume of solid generated about the x axis.




Example 3 cont

Example 3 cont

Solving differential equations n n n Separating the variables and then integrating. Sometimes you are given a differential equation with functions in terms of x and y. Find the GS of the following DE. Leave your answer y= f(x).


Solving differential equations n n n Separating the variables and then integrating. Sometimes you are given a differential equation with functions in terms of x and y. Find the GS of the following DE. Leave your answer y= f(x).

Example separating the variable. Find the GS of this DE
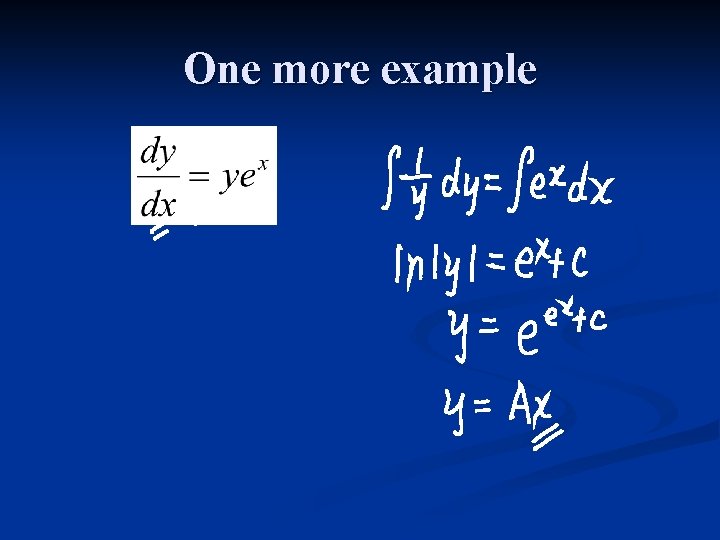
One more example



Real life applications! n The rate at which Ewoks increase in population at time t is given by d. P/dt=KP, where P is the population, K is a positive constant. In the beginning of time there were 8 Ewoks on earth and at time t=1 they grew to 56. Find the population at t=2.
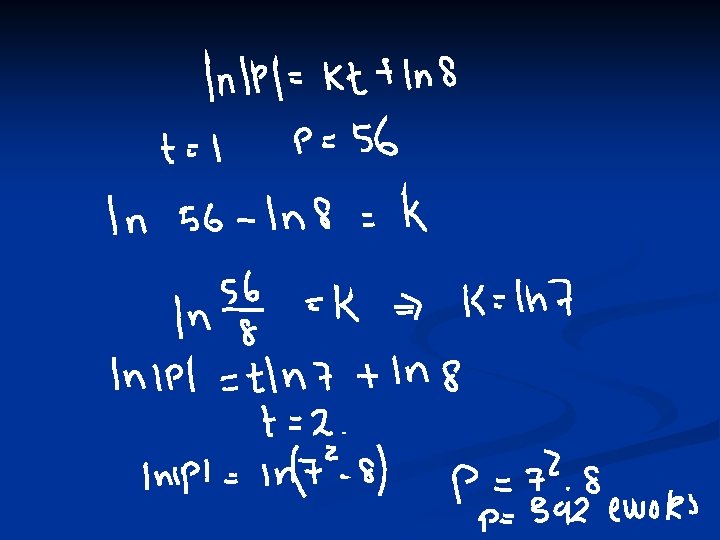

Mixed exercises n Example
 What is simultaneous integration
What is simultaneous integration Forward integration and backward integration
Forward integration and backward integration Vertical diversification example
Vertical diversification example Esme caitlin
Esme caitlin Esme sudria intranet
Esme sudria intranet Esme foundation
Esme foundation Intranet esme sudria
Intranet esme sudria . . . . they do their homework last night?
. . . . they do their homework last night? In go kiss the world the authors mother died in
In go kiss the world the authors mother died in Freedom personification
Freedom personification Sheryl forgot her purse so i lent her ten dollars
Sheryl forgot her purse so i lent her ten dollars Her fancy was running riot along those days ahead of her
Her fancy was running riot along those days ahead of her Her family calls her blessed
Her family calls her blessed They shall rise up and call her blessed
They shall rise up and call her blessed Theme of story meaning
Theme of story meaning Onomatopoeia in romeo and juliet act 2
Onomatopoeia in romeo and juliet act 2 A song of a mother to her firstborn meaning
A song of a mother to her firstborn meaning What is english 10-1
What is english 10-1 Ubiquitous computing nedir
Ubiquitous computing nedir A martian lander is approaching the surface
A martian lander is approaching the surface Approaching meeting exceeding
Approaching meeting exceeding Approaching differences diagram
Approaching differences diagram The sound of the approaching grain teams
The sound of the approaching grain teams Exceeding meeting approaching
Exceeding meeting approaching Why do motorcyclist use dipped headlights in daylight
Why do motorcyclist use dipped headlights in daylight Chapter 8 great gatsby analysis
Chapter 8 great gatsby analysis Extra coronal retainer
Extra coronal retainer Direct retention in rpd
Direct retention in rpd Approaching vehicle audible system
Approaching vehicle audible system The giver introduction
The giver introduction Double embrasure clasp
Double embrasure clasp Jcids process chart
Jcids process chart Language
Language Definite integral integration by parts
Definite integral integration by parts Google earth
Google earth Integration of power series
Integration of power series Bruce decleene
Bruce decleene Example of market integration
Example of market integration Impact of integration
Impact of integration Forward integration strategy examples
Forward integration strategy examples Integrated control and safety system
Integrated control and safety system Summit moodle
Summit moodle Ado integration adapters
Ado integration adapters Integration of dirac delta function
Integration of dirac delta function Explicit method is stable only if
Explicit method is stable only if Antiderivative class 12
Antiderivative class 12 Language integration
Language integration Bernoulli brothers
Bernoulli brothers Social integration
Social integration Communication integration processes
Communication integration processes Object oriented integration and system testing
Object oriented integration and system testing Post merger integration course
Post merger integration course Further applications of integration
Further applications of integration Data integration statistics
Data integration statistics Birt integration
Birt integration Dynamics 365 azure service bus integration
Dynamics 365 azure service bus integration Nomadic empires and eurasian integration
Nomadic empires and eurasian integration Sas data integration server
Sas data integration server Further applications of integration
Further applications of integration What did cornelius vanderbilt invent
What did cornelius vanderbilt invent Integration by parts lipet
Integration by parts lipet Nhs ers integration
Nhs ers integration Qlikview salesforce connector
Qlikview salesforce connector Simpson one third rule
Simpson one third rule Infusion curriculum integration
Infusion curriculum integration Fourier transform notation
Fourier transform notation Trapezoidal sum
Trapezoidal sum Inobiz
Inobiz Separatist view of ethics examples
Separatist view of ethics examples Ecomagination
Ecomagination Bilagsscanning
Bilagsscanning Ssush
Ssush How to calculate consumer surplus from equations
How to calculate consumer surplus from equations Vertical integration
Vertical integration Supplier onboarding process flow
Supplier onboarding process flow Block quotation example
Block quotation example Nike vertical integration
Nike vertical integration Kallidus zendesk
Kallidus zendesk Global integration definition
Global integration definition Jollibee horizontal integration
Jollibee horizontal integration Vertical integration supply chain
Vertical integration supply chain Weight center
Weight center Direct quote example
Direct quote example Integration design principles
Integration design principles Nfl draft
Nfl draft Functional silos
Functional silos