Imperative Programming Chapter 8 1 Local State Real

Imperative Programming Chapter 8 1

Local State Real world software like: • Banks • Course grading system Are state systems. i. e. they change along time: for example: current balance and current grade. 2

What is Imperative Programming? “In computer science, imperative programming is a programming paradigm that describes computation in terms of statements that change a program state (Wikipedia)” Not more expressive than FP! Just different 3

Imperative vs Functional Such systems (banks, courses) differ from the mathematical problems handled in previous chapters, like sequence summation or writing a language interpreter. 4

How to Model State? • Lazy Lists (see lecture notes) • More convectional: Object the has a changing state (computation is a sequence of states – remember automata? ) 5

The Imperative Programming Model • Imperative programming is characterized by: – Understanding variables as storage places (addresses) – Mutation operations – Operational semantics: computation is a sequence of states: <variable contents, place in program> 6

Mutation in Racket • Variable assignment: set! • Box type • Mutable data types (out of scope of this course) 7

Variable Assignment Modification of value of a defined variable > (define my-list (list 1 2 3)) > my-list ’(1 2 3) > (set! my-list (list 1 2 4)) > my-list ’(1 2 4) > (set! a 4). . set!: assignment disallowed; cannot set variable before its definition 8

The Box Type Values are references (or pointers) for values that can be changed during computation. • Constructor: box • Selector: unbox • Mutator: set-box! 9

Box Examples (1) (define a (box 7)) > (* 6 (unbox a)) 42 > a '#&7 > (set-box! a (+ (unbox a) 3)) > (* 6 (unbox a)) 60 10

Box Examples (2) > (define increase-last! (lambda (lst) (let ((last-el (last lst))) (set-box! last-el (add 1 (unbox lastel)))))) > (define l (map box ’(1 2 3 4))) > l ’(#&1 #&2 #&3 #&4) > (increase-last! l) > l ’(#&1 #&2 #&3 #&5) > (unbox (last l)) 5 11

Box Example (3): > (define circ-l (list (box 1) (box 2) (box 3))) > circ-l '(#&1 #&2 #&3) > (unbox (car circ-l)) 1 > (unbox (cadr circ-l)) 2 > (unbox (caddr circ-l)) 3 > (set-box! (caddr circ-l) > circ-l #0='(#&1 #&2 #&#0#) > (unbox (caddr circ-l)) #0='(#&1 #&2 #&#0#) > (eq? circ-l (unbox (caddr circ-l))) #t 12

The Box type: Type constructor: Value constructor: Selector: Mutator: Identifier: Value equality: Identity equality: procedure name box unbox set-box! box? equal? eq? BOX(T ) type [T → BOX(T )] [BOX(T ) → T] [BOX(T ) * T→ Void] [T → Boolean] [T 1 ∗ T 2 → Boolean] 13

Side Effects • Side effects are "non-functional" Their existence does not agree with the FP paradigm • set! and set-box! are side effects procedure • We have already seen two kinds of side effect procedures: define and the display procedure. • Side effects procedures are applied for the sake of their side effects, and not for their returned value, void • In imperative programming, it is meaningful to use sequences of expressions 14

State based modeling • Defining objects with a modifiable private fields (local variables), and a set of accessors (selectors and mutators) that have controlled access to the object's private fields. • All objects may have access to shared (static) variables. 15

Bank Account Withdrawal Example ; ; Signature: withdraw(amount) ; ; Purpose: Withdraw ’amount’ from a private ’balance’. ; ; Type: [Number -> Number] ; ; Post-condition: result = if balance@pre >= amount ; ; then balance@pre - amount ; ; else balance (define withdraw (let ([balance (box 100)]) (lambda (amount) (if (>= (unbox balance) amount) (begin (set-box! balance (- (unbox balance) amount)) (unbox balance)) (begin (display "Insufficient funds") (newline) (unbox balance)))))) 16

> withdraw #<procedure: withdraw> > (withdraw 25) 75 > (withdraw 25) 50 > (withdraw 60) Insufficient funds 50 > (withdraw 15) 35 17

Full Bank Account Example ; ; Signature: make-account(balance) ; ; Type: [Number -> [Symbol -> [Number -> Number]]] (define make-account (λ (balance) (let ((balance)) (letrec ((get-balance ( λ (amount) balance)) (set-balance! ( λ (amount) (set! balance amount))) (withdraw (λ (amount) (if (>= balance amount) (begin (set-balance! (- balance amount)) balance) (begin (display "Insufficient funds") (newline) balance)))) (deposit (λ (amount) (set-balance! (+ balance amount)) balance)) (dispatch (λ (m) (cond ((eq? m ’balance) get-balance) ((eq? m ’withdraw) ((eq? m ’deposit) (else (error ’make-account "Unknown request: ~s" m)))))) dispatch)))) 18

> (define acc (make-account 100)) > acc #<procedure: dispatch> > ((acc ’withdraw) 50 > ((acc ’withdraw) 60) Insufficient funds 50 > ((acc ’withdraw) 30) 20 > ((acc ’withdraw) 60) Insufficient funds 20 > (define acc 2 (make-account 100)) > ((acc 2 ’withdraw) 30) 70 > ((acc ’withdraw) 30) Insufficient funds 20 19

Mutable ADTs : Pair ; Type: [T 1*T 2 -> [Symbol -> Procedure]] ; The dispatch procedure returns procedures with different arities ; (Currying could help here). (define mpair (λ (x y) (letrec ((get-x (λ () x)) (get-y (λ () y)) (set-x! (λ (v) (set! x v))) (set-y! (λ (v) (set! y v))) (dispatch (lambda (m) (cond ((eq? m 'car) get-x) ((eq? m 'cdr) get-y) ((eq? m 'set-car!) set-x!) ((eq? m 'set-cdr!) set-y!) (else (error 'mpair "Undefined operation ~s" m))))) ) dispatch))) 20

Mutable ADTs : Pair (define mutable-car (λ (z) ((z ’car)))) (define mutable-cdr (λ (z) ((z ’cdr)))) (define set-car! (lambda (z new-value) ((z ’set-car!) new-value))) (define set-cdr! (lambda (z new-value) ((z ’set-cdr!) new-value))) 21

Mutable ADTs : Pair > > 1 > 2 > > 3 > > 4 >. (define p 1 (mpair 1 2)) (mutable-car p 1) (mutable-cdr p 1) (set-car! p 1 3) (mutable-car p 1) (set-cdr! p 1 4) (mutable-cdr p 1) (mutable-cdr (set-cdr! p 1 5)). procedure application: expected procedure, given: #<void>; arguments were: ’cdr 22

Lazy Pair (define lazy-mpair (λ (x y) (let ((x (box x)) (y (box y))) (λ (sel) (sel x y))))) (define lazy-set-car! (λ (z new-value) (z (λ (x y) (set-box! x new-value))))) (define lazy-mcar (λ (z) (z (λ (x y) (unbox x))))) (define lazy-set-cdr! (λ (z new-value) (z (λ (x y) (set-box! y new-value))))) (define lazy-mcdr (λ (z) (z (λ (x y) (unbox y))))) 23

Lazy Pair > > 1 > 2 > > 3 (define p 2 (lazy-mpair 1 2)) (lazy-mcar p 2) (lazy-mcdr p 2) (lazy-set-car! p 2 3) (lazy-mcar p 2) 24

Value Equality vs. Identity Equality Since we have states, we can check state equality or identity. • equal? – State (value) equality • eq? – Object equality 25

Value Equality vs. Identity Equality > (define x (list (box 'a) (box 'b))) > (define y (list (car x) (box 'c) (box 'd))) > (define z (list (box 'a) (box 'c) (box 'd)) ) > (define w y) > (eq? y w) ; identity #t > (eq? y z) #f > (equal? y z) ; value equality #t > (equal? (car z) (car x)) #t > (eq? (car z) (car x)) #f 26

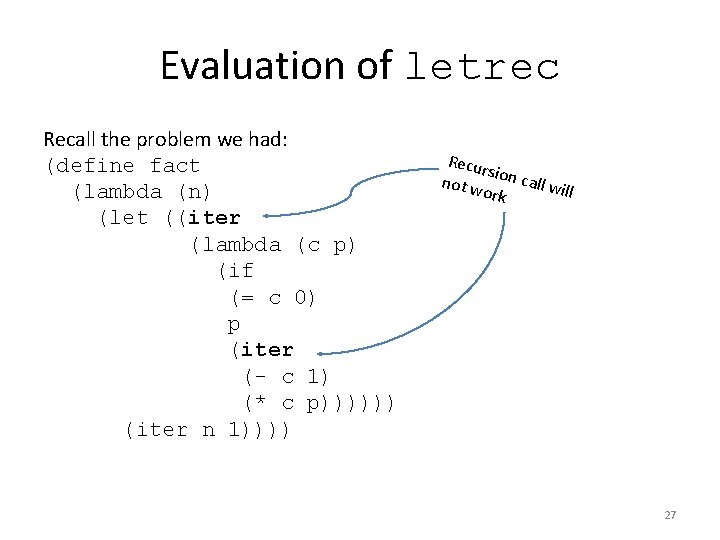
Evaluation of letrec Recall the problem we had: (define fact (lambda (n) (let ((iter (lambda (c p) (if (= c 0) p (iter (- c 1) (* c p)))))) (iter n 1)))) Recu rs not w ion call wi ll ork 27

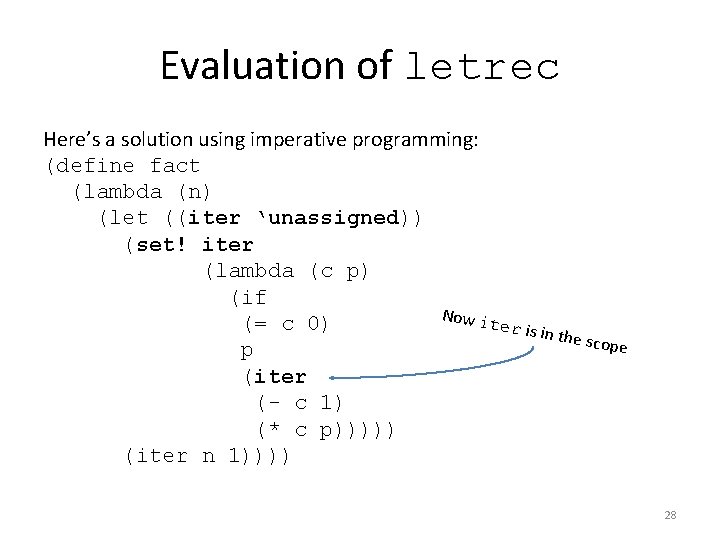
Evaluation of letrec Here’s a solution using imperative programming: (define fact (lambda (n) (let ((iter ‘unassigned)) (set! iter (lambda (c p) (if Now it (= c 0) er is in the sco pe p (iter (- c 1) (* c p))))) (iter n 1)))) 28

Evaluation of letrec • Now we unveil the secret of letrec… • Its semantics cannot be explained in FP (let ((f 1 ’unassigned). . . (fn ’unassigned)) (set! f 1 lambda-exp 1). . . (set! fn lambda-expn) e 1. . . em)) 29

Extending the Environment Model • The substitution model cannot support mutation • Semantics of set-binding!(x, val, <f 1, . . . , fn>) : 30

Extending the Environment Model • Add set! Special operator: env−eval[(set! x e), env] = set−binding!(x, env−eval[e, env], env) • Add Box type 31

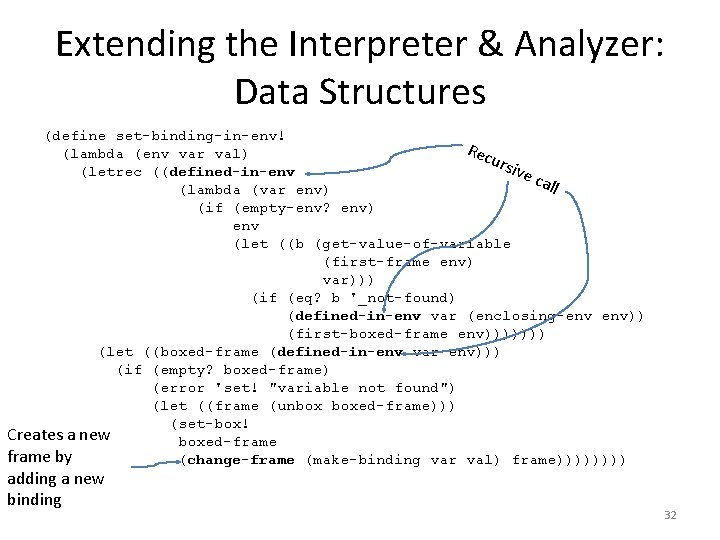
Extending the Interpreter & Analyzer: Data Structures (define set-binding-in-env! Rec (lambda (env var val) urs ive (letrec ((defined-in-env call (lambda (var env) (if (empty-env? env) env (let ((b (get-value-of-variable (first-frame env) var))) (if (eq? b '_not-found) (defined-in-env var (enclosing-env env)) (first-boxed-frame env))))))) (let ((boxed-frame (defined-in-env var env))) (if (empty? boxed-frame) (error 'set! "variable not found") (let ((frame (unbox boxed-frame))) (set-box! Creates a new boxed-frame by (change-frame (make-binding var val) frame)))) adding a new binding 32

Extending the Interpreter & Analyzer: Data Structures (define change-frame (lambda (binding frame) (let ((bvar (binding-variable binding)) (bval (binding-value binding))) (change-sub frame bvar bval)))) (define change-sub (lambda (sub var value) (let ((vars (get-variables sub)) (values (get-values sub))) (if (member vars) (make-sub (cons vars) (cons values)) (error 'change-sub "substitution is not defined on variable"))))) 33

Extending the Interpreter & Analyzer: Data Structures (define make-the-global-environment (lambda () (let* ((primitive-procedures (list 'car car) (list 'cdr cdr). . . (list 'box box) (list 'unbox) (list 'box? ) (list 'set-box!). . . 34

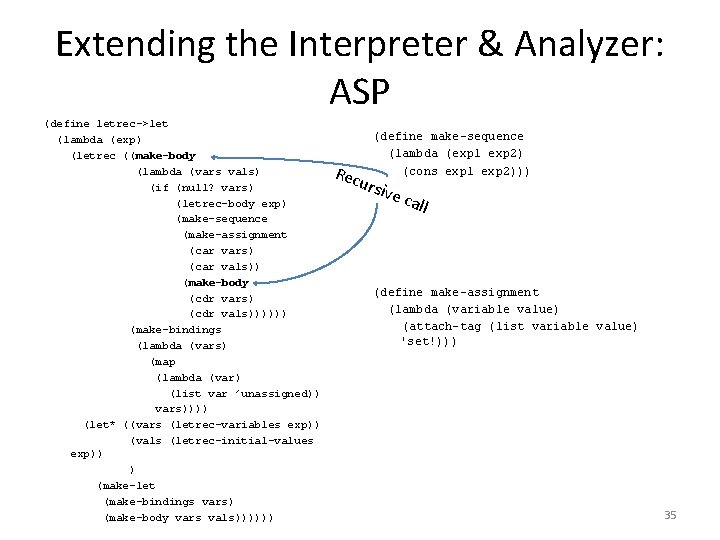
Extending the Interpreter & Analyzer: ASP (define letrec->let (lambda (exp) (letrec ((make-body (lambda (vars vals) (if (null? vars) (letrec-body exp) (make-sequence (make-assignment (car vars) (car vals)) (make-body (cdr vars) (cdr vals)))))) (make-bindings (lambda (vars) (map (lambda (var) (list var ’unassigned)) vars)))) (let* ((vars (letrec-variables exp)) (vals (letrec-initial-values exp)) ) (make-let (make-bindings vars) (make-body vars vals)))))) Rec (define make-sequence (lambda (exp 1 exp 2) (cons exp 1 exp 2))) ursi v e ca ll (define make-assignment (lambda (variable value) (attach-tag (list variable value) 'set!))) 35

Extending the Interpreter: env-eval (define eval-special-form (lambda (exp env) (cond. . . ((assignment? exp) (eval-assignment exp env))))) (define eval-assignment (lambda (exp env) (set-binding-in-env! env (assignment-variable exp) (env-eval (assignment-value exp) env)) 'ok)) 36

Extending the Analyzer (define analyze-assignment (lambda (exp) (let ((var (assignment-variable exp)) (val (analyze (assignment-value exp)))) (lambda (env) (set-binding-in-env! env var (val env)) ’ok)))) 37

Type Checking • (set! x e) is well typed if e is well typed • Typing rule for set! : For every: type assignment TA, expression e, and type expression S: If Tenv |- e: S, Tenv |- x: S, Then Tenv |- (set! x e): Void 38

Type Checking • Axiom for box For every type environment Tenv expression S: Tenv |- box: [S -> BOX(S)] Tenv |- unbox: [BOX(S) -> S] Tenv |- set-box!: [BOX(S)*S -> Tenv |- box? : [S -> Boolean] Tenv |- equal? : [BOX(S)*BOX(S) Boolean] Tenv |- eq? : [BOX(S)*BOX(S) -> and type Void] -> Boolean] 39

Course summary 1/3 General concepts: • semantics, types • syntax, CFG(BNF), • operational semantics, static analysis, renaming, substitution, interpretation(evaluation) • polymorphic types, type safety 40

Course summary 2/3 functional programming model – function definition and application – special forms – derived expressions, ASP – apply-procedure, environments, analysis – high-order procedures – variable binding, lexical scoping (dynamic scoping) – static type inference – pattern matching 41

Course summary 3/3 logic programming model – axioms and queries – proof trees, unification, pruning imperative programming – mutable data types – state based execution of assignments – local state encapsulation Techniques: CPS, ADTs, Currying , Sequences, lazy lists 42

Thank you for listening. Good luck on your exams. 43

44