Halliday D Resnick R and Walker J 2010













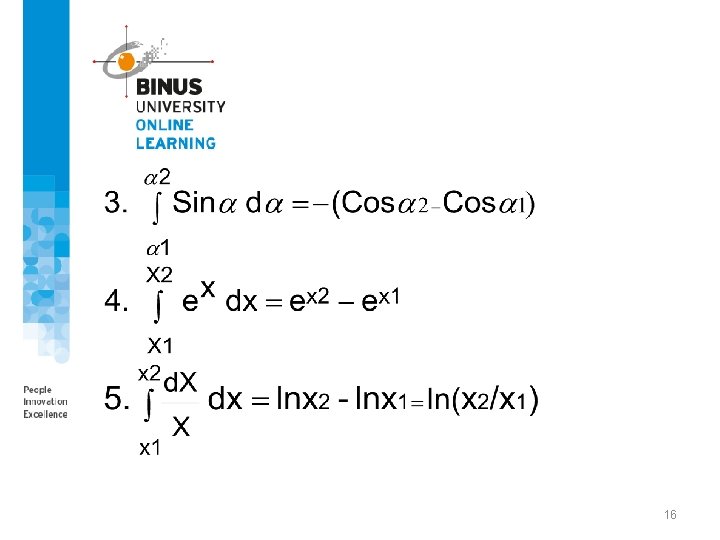

















- Slides: 37

Halliday D. ; Resnick R. and Walker J. (2010). Fundamentals Of Physics , Extended, ninth Edition , John Wiley & SONS Inc, New York, ISBN: 978 -0 -470 -55653 -5 1

SCIE 6004 – Physics I Week 1 Introduction and Vectors 2

Introduction 3

1. Measuring We discover physics by learning how to measure the quantities involve in physics. A physical quantity is a quantity that can be measured, and have the units. The physical quantity can be classified as : base (fundamental) quantities and derived quantities. ü Base quantities are the quantities that cannot be defined in terms of other quantities. There are : length, mass, time, electrical current, thermodynamic temperature, amount of substance, luminous intensity. 4

üDerived quantities are physics quantities derived from the base quantities through multiplication, division or both, some examples: force, velocity, acceleration, energy, …. . 2. International System of Units The SI system, or the International System of Units, is also called the metric system. The International System of Units(SI) is currently the generally accepted system of units in the physical sciences. 5

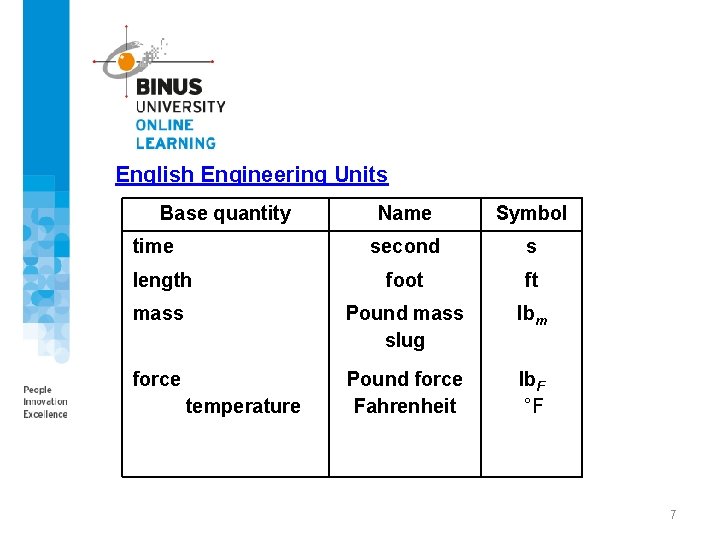
SI base units The SI is founded on seven SI base units for seven base quantities. Base quantity Length Mass Time Electric current Thermodynamic temperature Amount of substance Luminous Intensity Name Symbol meter kilogram second ampere kelvin m kg s A K mole Candela mol cd 6

English Engineering Units Base quantity Name Symbol second s length foot ft mass Pound mass slug lbm force Pound force Fahrenheit lb. F °F time temperature 7

Prefix For SI Units Factor Prefix Symbol 1024 yotta. Y 10 -1 deci d 1021 zetta. Z 10 -2 centic 1018 exa. E 10 -3 millim 1015 peta. P 10 -6 micro 1012 tera. T 10 -9 nanon 109 giga. G 10 -12 picop 106 mega. M 10 -15 femtof 103 kilok 10 -18 attoa 102 hektoh 10 -2 zeptoz 101 dekad 10 -24 yoctoy Scientific notation uses the power of 10. Example: 3 560 000 m = 3. 56 x 109 m. Sometimes special names are used to describe very large or very small quantities. For example, 2. 35 x 10 -9 = 2. 35 nanoseconds (ns) 8

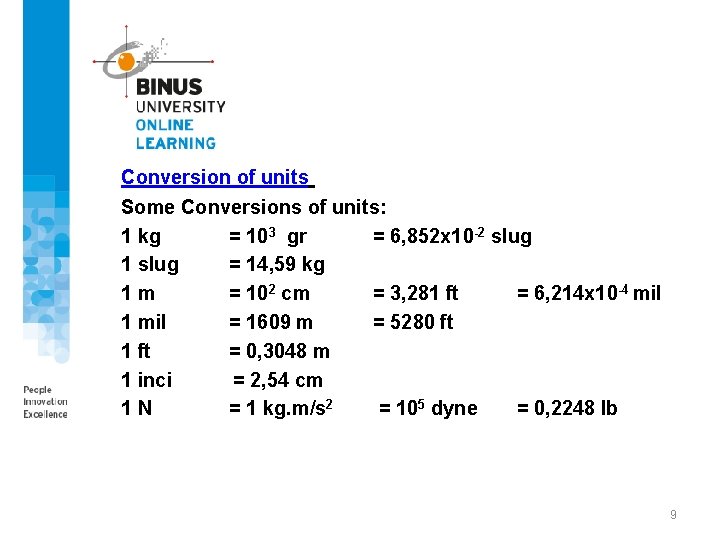
Conversion of units Some Conversions of units: 1 kg = 103 gr = 6, 852 x 10 -2 slug 1 slug = 14, 59 kg 1 m = 102 cm = 3, 281 ft = 6, 214 x 10 -4 mil 1 mil = 1609 m = 5280 ft 1 ft = 0, 3048 m 1 inci = 2, 54 cm 1 N = 1 kg. m/s 2 = 105 dyne = 0, 2248 lb 9

3. Review of Mathematics for Basic Physics (1) Trigonometric c b θ 900 a Sin θ = b / c Tan θ = b / a Sec θ = c / a Cos θ = a / c Cot θ = a / b Cosc θ = c / b Sin 2θ + Cos 2θ = 1 Sin 2θ = 2 Sin θ Cos 2θ = 1 - 2 Sin 2θ 10

PYTHAGOREAN THEOREM : a 2 + b 2 = c 2 Sin( α +β ) = Sin α Cos β + Sin β Cos α Cos( α +β ) = Cos α Cos β – Sin α Sin β (2) Quadratic Formula 11

(3) Derivatives 12

13

(4) Integrals Indefinite Integrals 14

Definite Integrals 15
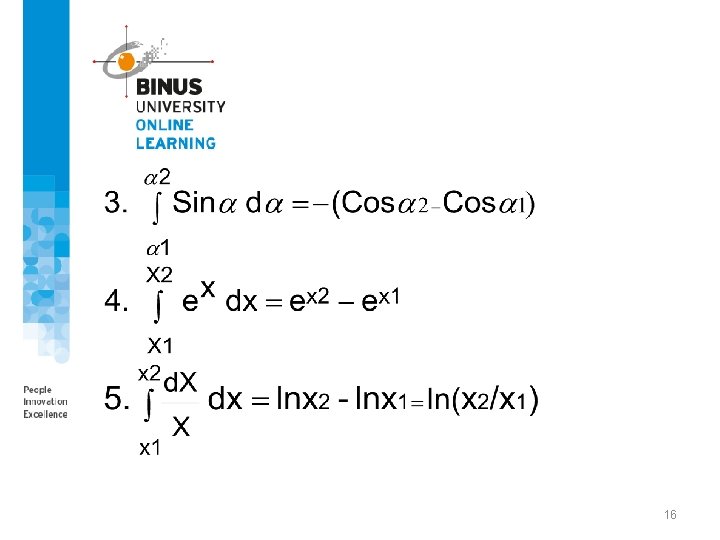
16

Vectors 17

Vectors 1. Vectors and Scalars Vectors: Quantities which indicate both magnitude and direction Examples: displacement, velocity, acceleration Scalars: Quantities which indicate only magnitude. Examples: Time, speed, temperature, distance 18

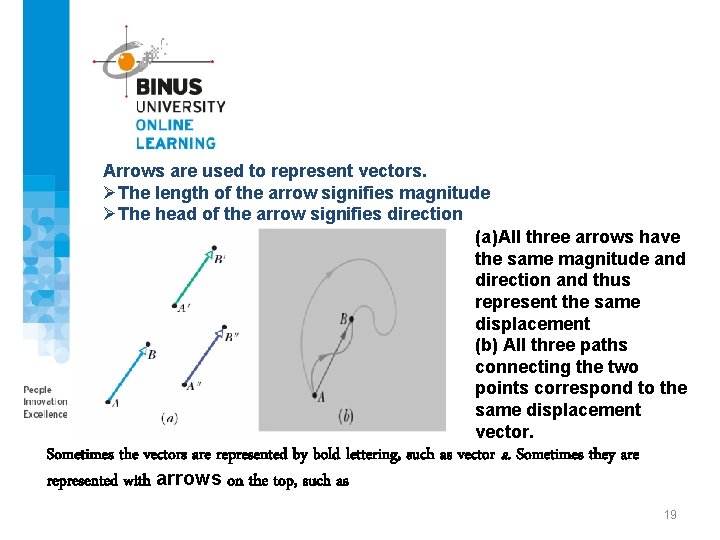
Arrows are used to represent vectors. ØThe length of the arrow signifies magnitude ØThe head of the arrow signifies direction (a)All three arrows have the same magnitude and direction and thus represent the same displacement (b) All three paths connecting the two points correspond to the same displacement vector. Sometimes the vectors are represented by bold lettering, such as vector a. Sometimes they are represented with arrows on the top, such as 19

2. Adding vectors geometrically Vector a and vector b can be added geometrically to yield the resultant vector sum S. Place the second vector b , with its tail touching the head of the first vector a. The vector sum S is the vector joining the tail of a to the head of b. 20

The Parallelogram method - draw vector A using appropriate scale and in the direction of its action - from the tail of vector A draw vector scale in the direction of its action B using the same - complete the parallelogram by using vectors A and B as sides of the parallelogram - the resulting vector is represented in both magnitude and direction by the diagonal of the parallelogram: C=A+B 21

22

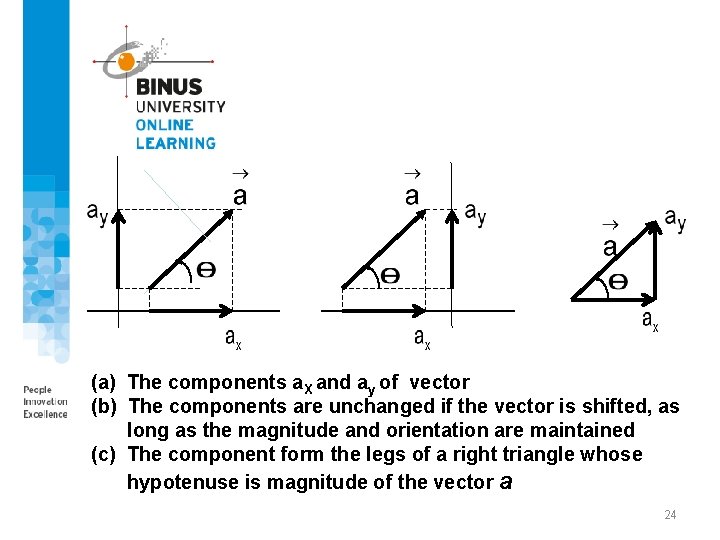
3. Components of vectors The component of a vector along an axis is the projection of the vector on to that axis. The process of finding the components of a vector is called resolution of the vector. In 3 -dimensions, there are three components of a vector along predefined x-, y-, and z-axes. 23

(a) The components a. X and ay of vector (b) The components are unchanged if the vector is shifted, as long as the magnitude and orientation are maintained (c) The component form the legs of a right triangle whose hypotenuse is magnitude of the vector a 24

Example, vectors: A small airplane leaves an airport on an overcast day and is later sighted 215 km away, in a direction making an angle 0 f 220 east of due north. How far east and north is the airplane from the airport when sighted? 25

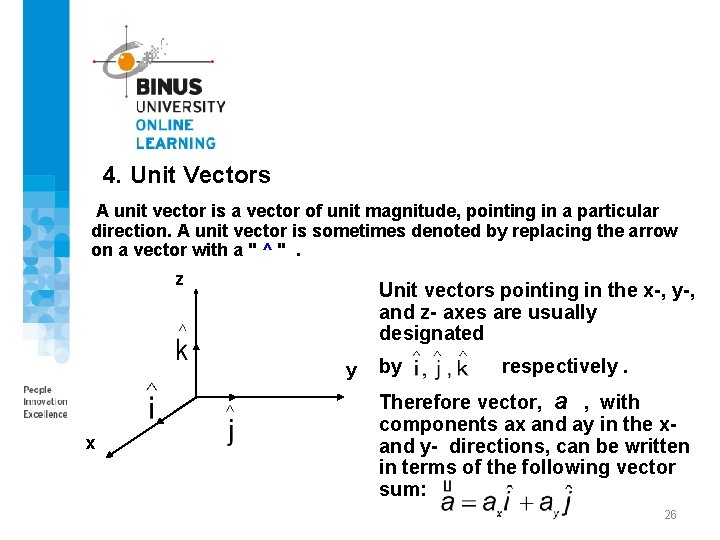
4. Unit Vectors A unit vector is a vector of unit magnitude, pointing in a particular direction. A unit vector is sometimes denoted by replacing the arrow on a vector with a " ^ ". z Unit vectors pointing in the x-, y-, and z- axes are usually designated y x by respectively. Therefore vector, a , with components ax and ay in the xand y- directions, can be written in terms of the following vector sum: 26

5. Adding vectors by components Therefore, two vectors must be equal if their corresponding components are equal. The procedure of adding vectors also applies to vector subtraction. 27

6. Multiplying vectors a. Multiplying a vector by a scalar changes the magnitude but not the direction: 28

b. Multiplying a vector by a vector: Scalar (Dot) Product Here, a and b are the magnitudes of vectors a and b respectively, and θ is the angle between the two vectors. The right hand side is a scalar quantity. 29

C. Multiplying a vector with a vector: Vector (Cross) Product Here, a and b are the magnitudes of vectors a and b respectively, and θ is the smaller of the two angles between a and b vectors. 30

Multiplying vectors; vector product in unit-vector notation: 31

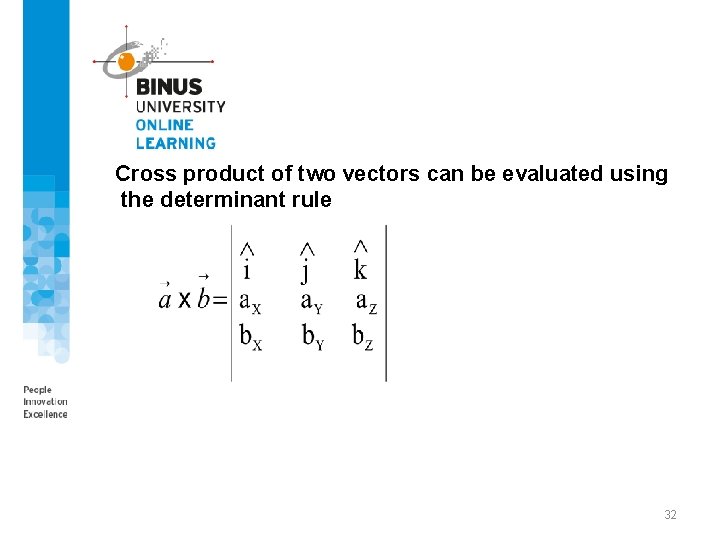
Cross product of two vectors can be evaluated using the determinant rule 32

Properties of the cross product 33

34

We next evaluate each term with Eq. c=ab. Sinθ , finding the direction with the right-hand rule. For the first term here, the angle θ between two vectors being crossed is 0. For the other terms θ is 90. We find This vector C is perpendicular to both a and b , a fact you can check by showing that c. a = 0 ; that is there is no component of vector c along the direction of either a or b. 35

Reference. Halliday D. ; Resniick R. and Walker J. (2010). Fundamentals Of Physics , ninth Edition , John Wiley & SONS Inc, New York, ISBN: 978 -0 -470 -55653 -5 36

Thank You 37
 Eun and resnick
Eun and resnick Resnick
Resnick Resnick
Resnick Algoritma scratch
Algoritma scratch Abi test results
Abi test results Dr. resnick
Dr. resnick Phatic function of language
Phatic function of language Campo tenor y modo
Campo tenor y modo Halliday 1993
Halliday 1993 Field tenor mode examples
Field tenor mode examples Halimbawa ng gamit ng wika sa lipunan
Halimbawa ng gamit ng wika sa lipunan Funciones del lenguaje halliday
Funciones del lenguaje halliday Jo halliday
Jo halliday Halliday
Halliday Halliday
Halliday General physics halliday
General physics halliday Halliday
Halliday Halliday
Halliday Halliday
Halliday Halliday
Halliday Halliday
Halliday Halliday
Halliday Interpretar
Interpretar Paul maidment
Paul maidment The devil and tom walker vocabulary
The devil and tom walker vocabulary Mood of the devil and tom walker
Mood of the devil and tom walker Quotas can act as a motivator as well as demotivator
Quotas can act as a motivator as well as demotivator Characteristics of the devil archetype
Characteristics of the devil archetype The devil and tom walker worksheet
The devil and tom walker worksheet Symbolism in the devil and tom walker
Symbolism in the devil and tom walker The devil and tom walker summary
The devil and tom walker summary Symbols in the devil and tom walker
Symbols in the devil and tom walker Why doesn't tom accept the devil's first offer
Why doesn't tom accept the devil's first offer The devil and tom walker reading check answers
The devil and tom walker reading check answers Multi choice
Multi choice Walker cell and hadley cell
Walker cell and hadley cell Andrew and ashton walker
Andrew and ashton walker Devil and tom walker
Devil and tom walker