Graphics CSCI 343 Fall 2019 Lecture 16 Viewing

Graphics CSCI 343, Fall 2019 Lecture 16 Viewing I 1

Viewing _ Viewing refers to positioning the camera in a coordinate frame and projection of the 3 D object onto the 2 D image plane of the camera. _ Positioning the camera is very similar to positioning an object. Moving the camera relative to an object is the same as moving the object relative to the camera, in the opposite direction. _ In open. GL the modeling and viewing transformations are combined into one transformation matrix. _ First the object is positioned by multiplying the vertices by the object transformation matrices. _ Then the camera is positioned by multiplying by camera transformation matrices. 2

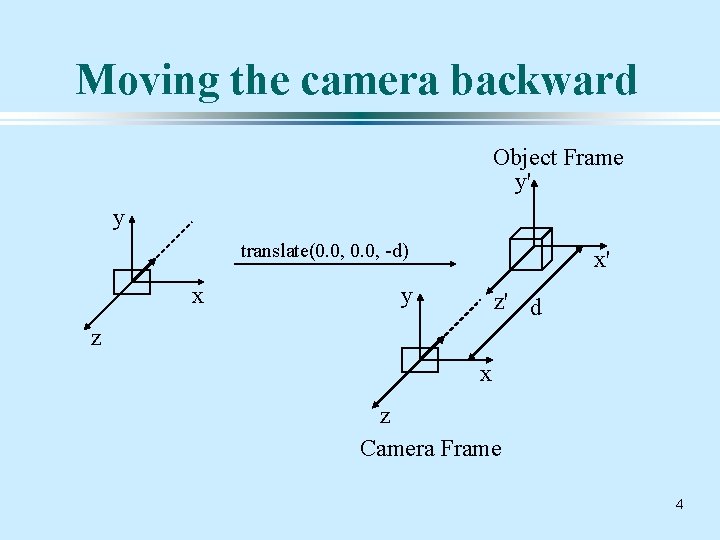
Default Position of Camera _The default camera position is centered at the origin, pointing along the negative Z axis. _If we create an object (e. g. a cube) centered on the origin, part of it will be behind the camera. _To gain a view of the entire object, we need to move the camera by a distance, d, along the positive Z axis. _This is equivalent to moving the object by a distance, -d, along the negative Z axis. 3

Moving the camera backward Object Frame y' y translate(0. 0, -d) x x' y z' d z x z Camera Frame 4

Looking at the side of an Object To move the camera to look at the side of an object that is centered on the origin: 1. Rotate the camera 90 deg. (Equivalent to rotating the object by -90 deg) 2. Translate the camera backward along +Z axis. (Equivalent to translating the object along -Z axis) mv. Matrix = translate(0. 0, -d); mv. Matrix = mult(mv. Matrix, rotate(-90. 0, 1. 0, 0. 0)); 5

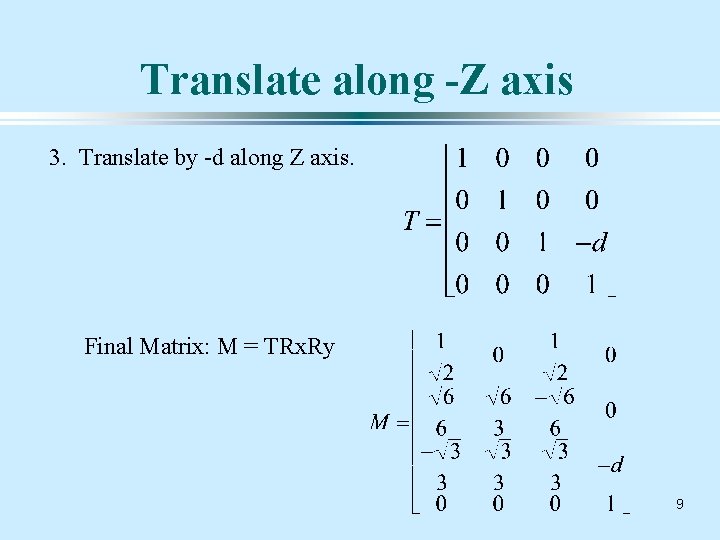
Isometric view of a cube The isometric view of a cube, is one in which the projection plane is placed symmetrically with respect to 3 faces of the cube. We can gain an isometric view by rotating the camera (or cube centered on the origin), first about the Y axis and then about the X axis. We then translate the camera backward to view it. M = TRx. Ry 6

Rotation matrix for Rotation about the Y axis 1. Rotate the cube 45 deg about the Y axis. 2 x z Top-down view after 45 deg rotation Ry = ? 7

Rotation Matrix for Rotation about Y axis 2. Rotate about the X Axis: y z 1 q Slice through Y-Z plane. (Through diagonal of cube) Rx = ? 8

Translate along -Z axis 3. Translate by -d along Z axis. Final Matrix: M = TRx. Ry 9

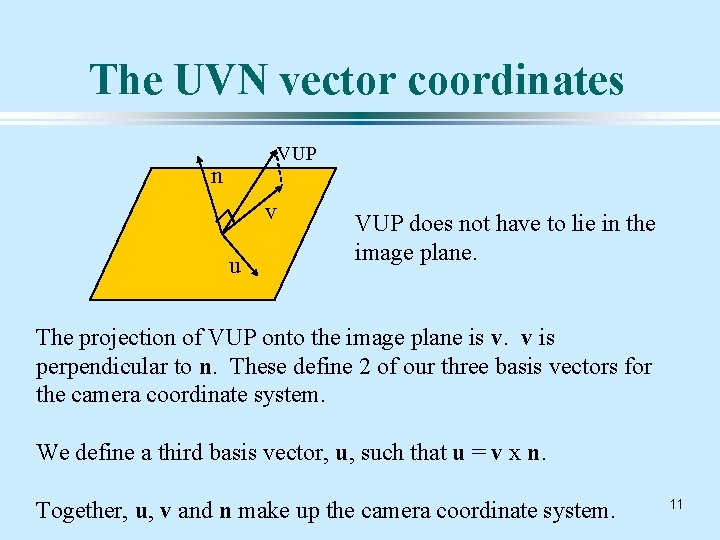
The UVN System Other graphics systems may define the camera viewing plane differently. The U-V-N system is one example: The camera plane is defined by 3 parameters: _ View Reference Point (VRP): A point (in the world frame) indicating the center of the camera's image plane. This specifies the position of the camera in space. _ View Plane Normal (VPN): A unit vector perpendicular to the camera's image plane. This specifies the orientation of the camera. _ View Up (VUP): A vector indicating the up direction (in world coordinates) for the camera. 10

The UVN vector coordinates VUP n v u VUP does not have to lie in the image plane. The projection of VUP onto the image plane is v. v is perpendicular to n. These define 2 of our three basis vectors for the camera coordinate system. We define a third basis vector, u, such that u = v x n. Together, u, v and n make up the camera coordinate system. 11

The look-at function allows the camera to remain aimed at a given point even as its position in the world changes. The camera is centered at the eye (VRP = e) The camera is pointed at the "at" point (VPN = a - e) The up vector (VUP) must be defined to specify the camera orientation. a VPN e In MV. js: function look. At( eye, at, up ) 12

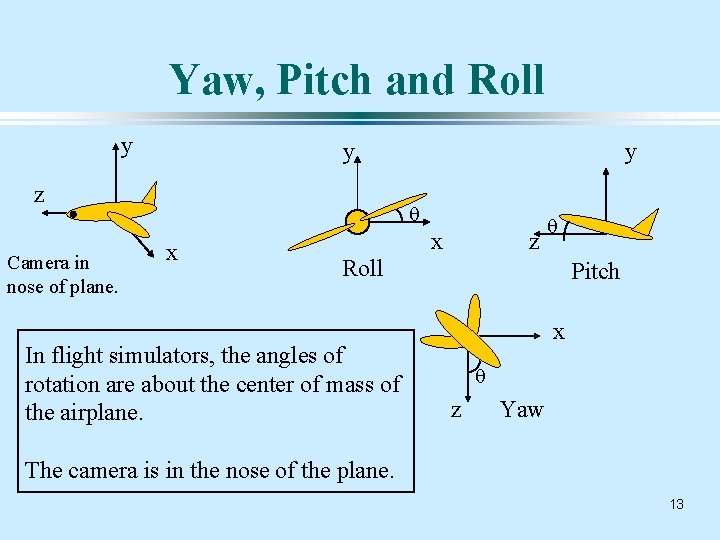
Yaw, Pitch and Roll y y z Camera in nose of plane. y q x x z q Roll In flight simulators, the angles of rotation are about the center of mass of the airplane. Pitch x q z Yaw The camera is in the nose of the plane. 13

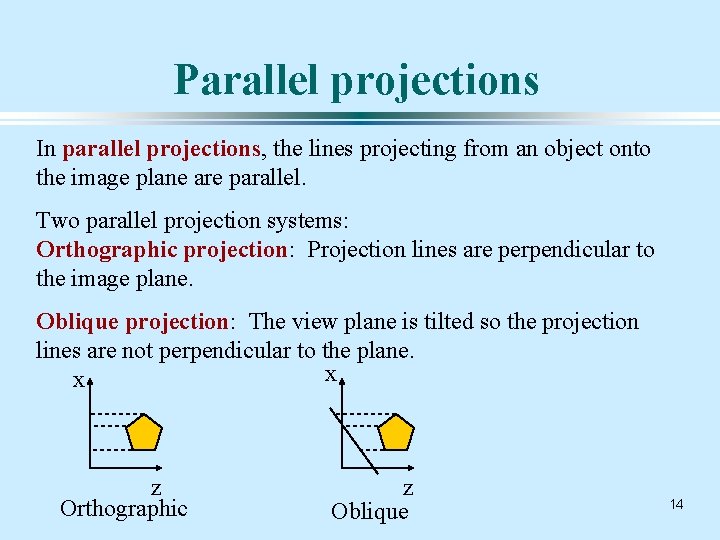
Parallel projections In parallel projections, the lines projecting from an object onto the image plane are parallel. Two parallel projection systems: Orthographic projection: Projection lines are perpendicular to the image plane. Oblique projection: The view plane is tilted so the projection lines are not perpendicular to the plane. x x z Orthographic z Oblique 14

Matrix for Orthographic Projection xp = x yp = y zp = 0 M=? p'= Mp = ? 15

Perspective Projection y (X, -Z) (yp, -d) -d (Y, -Z) -z -z x (xp, -d) -d 16

Matrix for Perspective Projection Representation of a point, P, in homogeneous coordinates: Perspective projection Matrix: 17