GoodnessofFit Tests with Censored Data Edsel A Pena

Goodness-of-Fit Tests with Censored Data Edsel A. Pena Statistics Department University of South Carolina Columbia, SC [E-Mail: pena@stat. sc. edu] Talk at Cornell University, 3/13/02 Research support from NIH and NSF. 1

Practical Problem 2

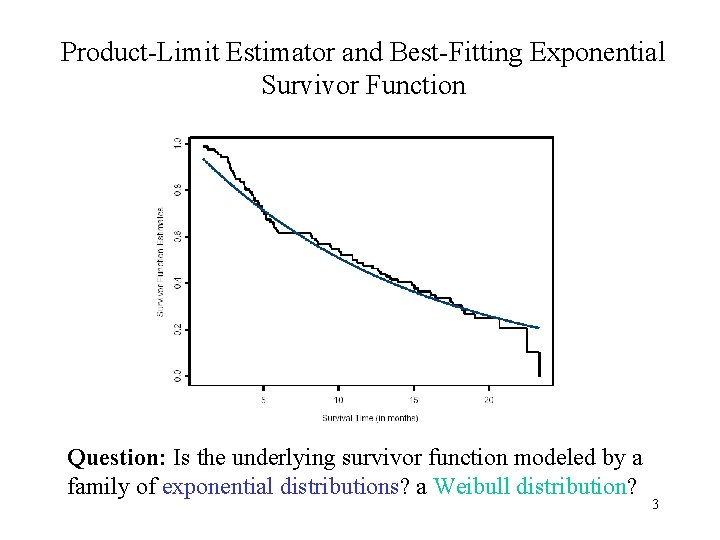
Product-Limit Estimator and Best-Fitting Exponential Survivor Function Question: Is the underlying survivor function modeled by a family of exponential distributions? a Weibull distribution? 3

A Car Tire Data Set • Times to withdrawal (in hours) of 171 car tires, withdrawal either due to failure or right-censoring. • Reference: Davis and Lawrance, in Scand. J. Statist. , 1989. • Pneumatic tires subjected to laboratory testing by rotating each tire against a steel drum until either failure (several modes) or removal (right-censoring). 4

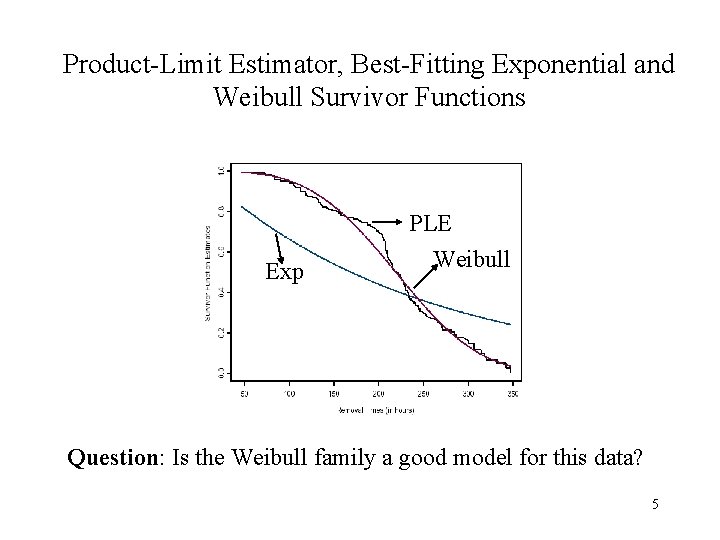
Product-Limit Estimator, Best-Fitting Exponential and Weibull Survivor Functions PLE Exp Weibull Question: Is the Weibull family a good model for this data? 5

Goodness-of-Fit Problem • T 1, T 2, …, Tn are IID from an unknown distribution function F • Case 1: F is a continuous df • Case 2: F is discrete df with known jump points • Case 3: F is a mixed distribution with known jump points • C 1, C 2, …, Cn are (nuisance) variables that right-censor the Ti’s • Data: (Z 1, d 1), (Z 2, d 2), …, (Zn, dn), where Zi = min(Ti, Ci) and di = I(Ti < Ci) 6

Statement of the GOF Problem On the basis of the data (Z 1, d 1), (Z 2, d 2), …, (Zn, dn): Simple GOF Problem: For a pre-specified F 0, to test the null hypothesis that H 0: F = F 0 versus H 1: F F 0. Composite GOF Problem: For a pre-specified family of dfs F = {F 0(. ; h): h G}, to test the hypotheses that H 0: F F versus H 1: F F. 7

Generalizing Pearson With complete data, the famous Pearson test statistics are: Simple Case: Composite Case: where Oi is the # of observations in the ith interval; Ei is the expected number of observations in the ith interval; and is the estimated expected number of observations in the ith interval under the null model. 8

Obstacles with Censored Data • With right-censored data, determining the exact values of the Oj’s is not possible. • Need to estimate them using the product-limit estimator (Hollander and Pena, ‘ 92; Li and Doss, ‘ 93), Nelson-Aalen estimator (Akritas, ‘ 88; Hjort, ‘ 90), or by self-consistency arguments. • Hard to examine the power or optimality properties of the resulting Pearson generalizations because of the ad hoc nature of their derivations. 9

In Hazards View: Continuous Case For T an abs cont +rv, the hazard rate function (t) is: Cumulative hazard function (t) is: Survivor function in terms of : 10

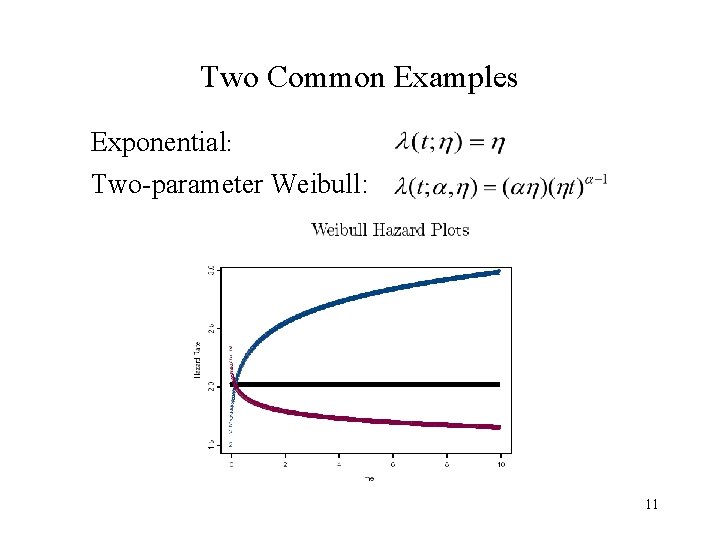
Two Common Examples Exponential: Two-parameter Weibull: 11

Counting Processes and Martingales {M(t): 0 < t} is a square-integrable zero-mean martingale with predictable quadratic variation (PQV) process 12

Idea in Continuous Case • For testing H 0: (. ) C ={ 0(. ; h): h G}, if H 0 holds, then there is some h 0 such that the true hazard 0(. ) is such 0(. ) = 0(. ; h 0) • Let K • Basis Set for K: • Expansion: • Truncation: , p is smoothing order 13

Hazard Embedding and Approach • From this truncation, we obtain the approximation • Embedding Class Cp • Note: H 0 Cp obtains by taking = 0. • GOF Tests: Score tests for H 0: = 0 versus H 1: 0. • Note that h is a nuisance parameter in this testing problem. 14

Class of Statistics • Estimating equation for the nuisance h: • Quadratic Statistic: • is an estimator of the limiting covariance of 15

Asymptotics and Test • Under regularity conditions, • Estimator of X obtained from the matrix: • Test: Reject H 0 if 16

A Choice of Generalizing Pearson • Partition [0, t] into 0 = a 1 < a 2 < … < ap = t, and let • Then • are dynamic expected frequencies 17

Special Case: Testing Exponentiality • Exponential Hazards: C = { 0(t; h)=h} with • Test Statistic (“generalized Pearson”): where 18

A Polynomial-Type Choice of • Components of where • Resulting test based on the ‘generalized’ residuals. The framework allows correcting for the estimation of nuisance h. 19

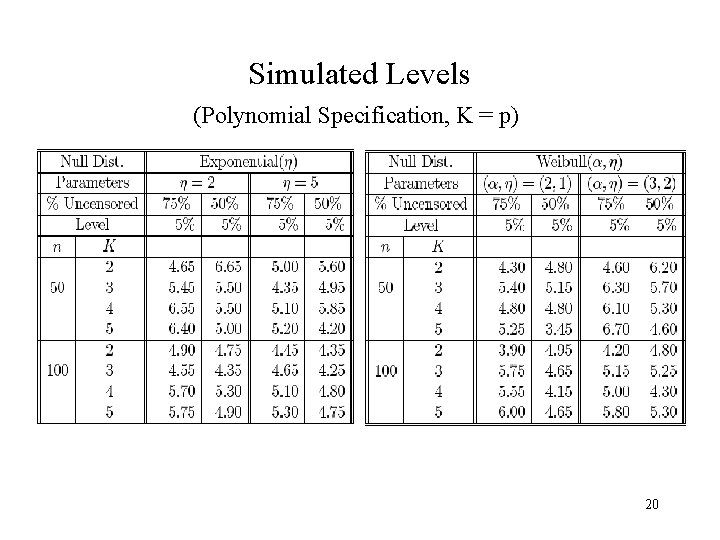
Simulated Levels (Polynomial Specification, K = p) 20

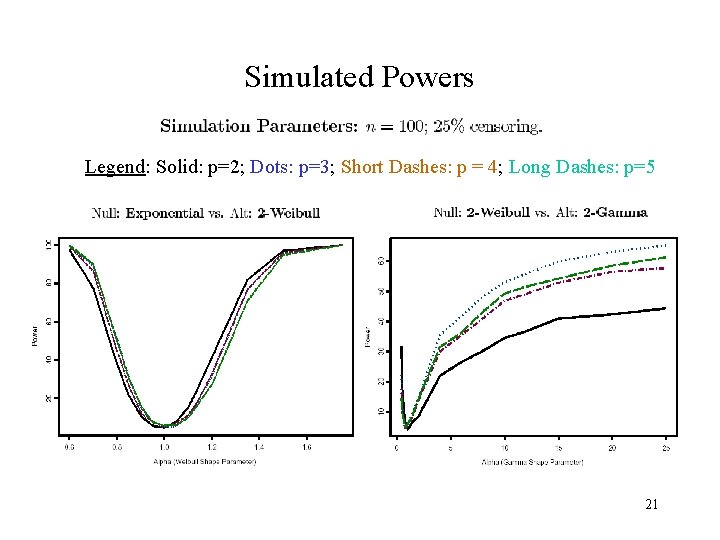
Simulated Powers Legend: Solid: p=2; Dots: p=3; Short Dashes: p = 4; Long Dashes: p=5 21

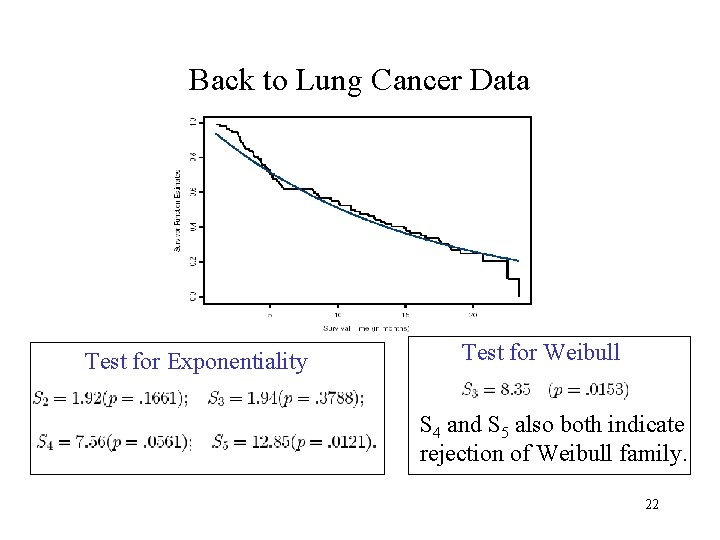
Back to Lung Cancer Data Test for Exponentiality Test for Weibull S 4 and S 5 also both indicate rejection of Weibull family. 22

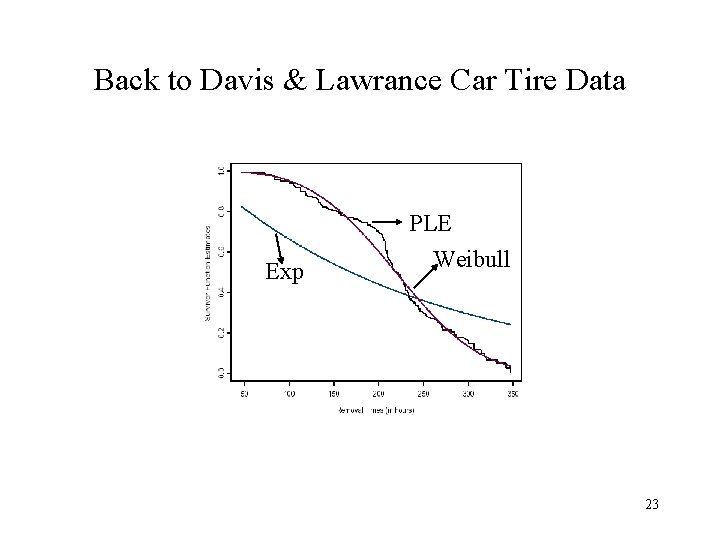
Back to Davis & Lawrance Car Tire Data PLE Exp Weibull 23

Test of Exponentiality Conclusion: Exponentiality does not hold as in graph! 24

Test of Weibull Family Conclusion: Cannot reject Weibull family of distributions. 25

Simple GOF Problem: Discrete Data • Ti’s are discrete +rvs with jump points {a 1, a 2, a 3, …}. • Hazards: • • Problem: To test the hypotheses based on the right-censored data (Z 1, d 1), …, (Zn, dn). 26

• True and hypothesized hazard odds: • For p a pre-specified order, let be a p x J (possibly random) matrix, with its p rows linearly independent, and with [0, a. J] being the maximum observation period for all n units. 27

Embedding Idea • To embed the hypothesized hazard odds into • Equivalent to assuming that the log hazard odds ratios satisfy • Class of tests are the score tests of H 0: q = 0 vs. H 1: q 0 as p and are varied. 28

Class of Test Statistics • Quadratic Score Statistic: p • Under H 0, this converges in distribution to a chi-square rv. 29

A Pearson-Type Choice of Partition {1, 2, …, J}: 30

A Polynomial-Type Choice quadratic form from the above matrices. 31

Hyde’s Test: A Special Case When p = 1 with polynomial specification, we obtain: Resulting test coincides with Hyde’s (‘ 77, Btka) test. 32

Adaptive Choice of Smoothing Order = partial likelihood of = associated observed information matrix = partial MLE of Adjusted Schwarz (‘ 78, Ann. Stat. ) Bayesian Information Criterion * 33

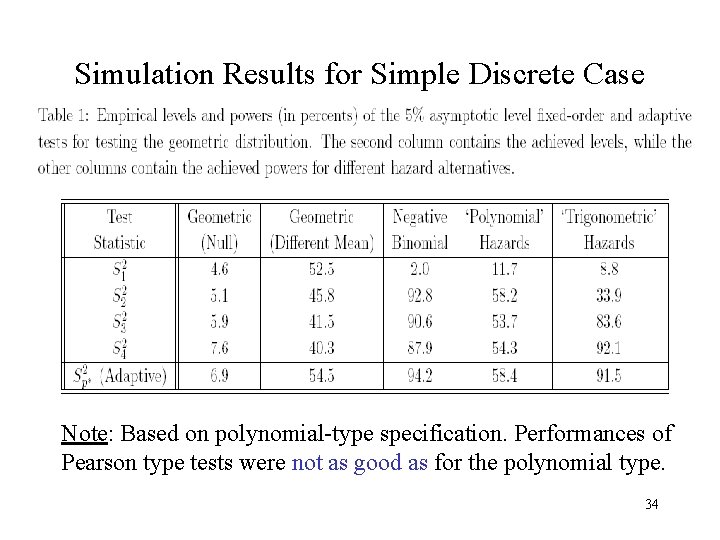
Simulation Results for Simple Discrete Case Note: Based on polynomial-type specification. Performances of Pearson type tests were not as good as for the polynomial type. 34

Concluding Remarks • Framework is general enough so as to cover both continuous and discrete cases. • Mixed case dealt with via hazard decomposition. • Since tests are score tests, they possess local optimality properties. • Enables automatic adjustment of effects due to estimation of nuisance parameters. • Basic approach extends Neyman’s 1937 idea by embedding hazards instead of densities. • More studies needed for adaptive procedures. 35